Categorie: Matematica
Tags: geometria ghiaccio Papalla quiz sci strada più corta
Scritto da: Vincenzo Zappalà
Commenti:16
La strada di montagna: quasi-quiz conico. Prima parte **
Si può sciare su Papalla? In un posto solo, dove si erge, nella sua maestosità, un monte conico coperto di ghiaccio e neve, di forma perfetta. I papalliani hanno deciso di costruire, finalmente, una strada per venire incontro ai tanti papalsciatori.
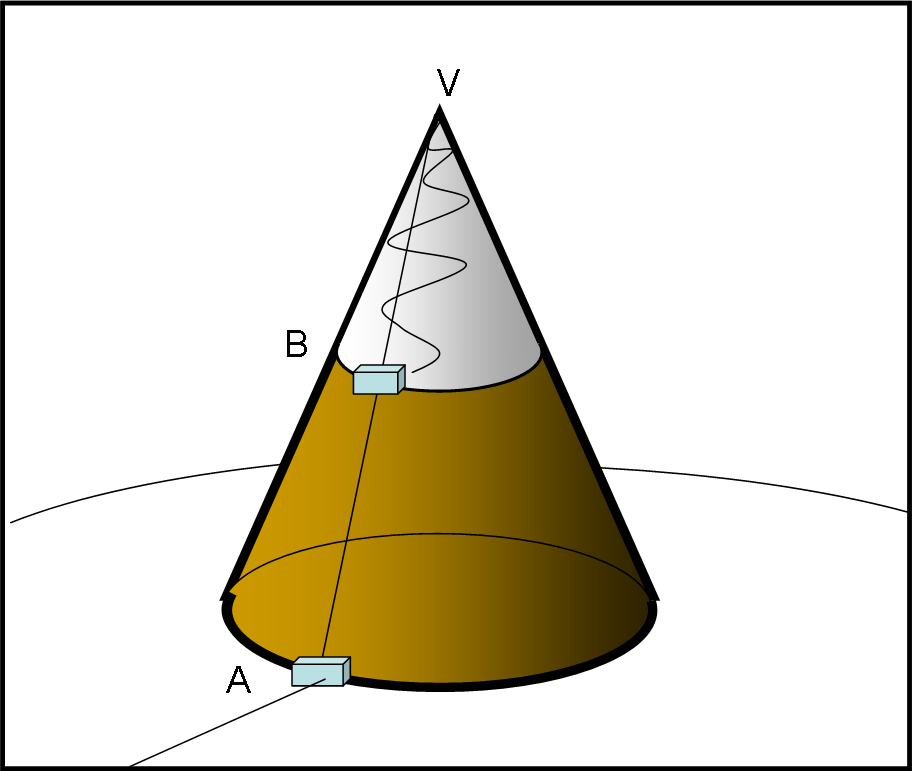
Su Papalla esiste un solo monte che interrompe la perfetta superficie sferica del pianeta. Viene chiamato Monte Cono per la sua forma estremamente regolare. La parte bassa è composta da terreno polveroso e roccioso, mentre la parte alta è sempre coperta di ghiaccio e neve. Sia la base del monte che la linea del ghiaccio sono circonferenze perfette equidistanti dalla cima (insomma, rappresentano coni retti, ossia ottenuti dalla rotazione intorno all’asse di triangoli rettangoli).
Fino ad oggi l’unico modo di raggiungere la zona delle piste da sci era prendere la vecchia funivia AB, che continuava fino alla vetta V, da dove partiva la pista più severa. Tuttavia, ormai le papalauto hanno invaso il pianeta e si è deciso di costruire una strada che permetta di raggiungere la zona B ad alta quota, partendo dalla base A.
Ovviamente, è impensabile costruire una strada che congiunga direttamente A con B (troppo ripido il pendio!) e allora si è deciso che la strada compia almeno un giro competo attorno al cono.
La squadra di tecnici comincia a studiare il percorso più breve, ma un giovane papalgeometra blocca subito i lavori. “Cari colleghi”, dice, “non riusciremo mai nel tentativo, dato che saremo costretti ad attraversare il ghiacciaio. Dobbiamo allungare il percorso”. Molti colleghi più anziani lo guardano con un sorriso malizioso. “Caro il nostro giovane “geometra”, basterà salire lentamente e continuamente lungo il pendio e arriveremo in B senza nemmeno sfiorare il ghiaccio”. Papalgeometra solleva le spalle: “Provateci pure, ma sicuramente allungherete il percorso. Non ci credete? Bene, potreste fare una prova facile facile, senza costruire la strada, ma rimanendo in piano, partendo da A e tornando in A”. Nel frattempo, un altro giovane papallo di passaggio esclama: “E vi va bene che la montagna è molto ripida, se no dovreste proprio scegliere una strada alternativa, più lunga!”
Che dire? Su Papalla sanno tutto della sfera, ma sul cono sparano un po’ a raffica. Volete spiegare per bene cosa si potrà fare sulla montagna e confermare o negare ciò che dicono i giovani “saputelli” e/o gli esperti più anziani?
QUI la soluzione e la seconda parte del quiz
QUI troverete altri percorsi da calcolare!
16 commenti
Non sono certo di avere capito ciò che intende il geometra. Cioè che salendo da A a B lungo una strada di data pendenza e compiendo almeno un giro completo attorno all'asse del cono si va a finire non in B ma oltre B, quindi invadendo in parte la zona del ghiacciaio ? Inoltre, non ho proprio capito cosa vuole dire quando suggerisce di fare una prova rimanendo in piano.
Comunque, io ho ragionato come segue e, sempre se ho capito bene, mi pare che una strada che parta da A e vada a finire esattamente in B compiendo un giro attorno all'asse del cono si possa realizzare.
Significato dei simboli utilizzati di seguito:
H= altezza del cono al vertice
Hb= quota del punto B rispetto alla base del cono
R= raggio di base del cono
x, y, z = coordinate del generico punto P lungo la strada
Per quella che è la geometria di un cono retto , la proiezione sul piano xy del raggio vettore OP è data da:
r(z) = R (H-z)/H (1)
Poiché non ci si muove lungo la congiungente AB ma lungo una strada di data pendenza, la quota del generico punto P è a sua volta funzione dell'angolo
. Quando tale angolo è zero, cioè alla partenza, la quota è zero, cioè il punto P coincide con il punto A. Invece, quando l'angolo è 360°, cioè a quello che deve essere l'arrivo, la quota deve essere pari a quella del punto B. Questo nel caso in cui la strada faccia solo un giro completo attorno all'asse del cono. Se di giri ne fa di più naturalmente diminuisce la pendenza della strada ma resta la relazione tra quota del generico punto P della strada e angolo 
. Nel caso preso in considerazione tale relazione è :
z(
) = Hb * 
/ 360°
Sostituendo questa espressione nella (1), ottengo:
r(
) = R(H-Hb * 
/360°)/H
In definitiva le coordinate del generico punto P lungo la strada avente le caratteristiche richieste sono:
x(P)= [R(H-Hb *
/360°)/H] *cos(
)
y(P)= [R(H-Hb *
/360°)/H] *sen(
)
z(P)= Hb *
/ 360°
In pratica il punto P si muove lungo un' elica conica che parte da A e va finire in B.
Allego immagine :
Qui, al solito, l'animazione del punto P che parte da A e arriva in B percorrendo la suddetta elica:
https://ggbm.at/gnqSzDe9
(quando si resetta, per cancellare anche la traccia del punto P ingrandire leggermente la vista grafica con la rotella del mouse)
Devo dire che neppure io ho ben capito cosa intenda dire il giovane geometra. Mi sembra che l'animazione di Arturo dia la risposta. Volendo interpretare il riferimento al piano mi viene da pensare alla figura dello sviluppo del tronco di cono e al tracciato della strada che si vederebbe su questo sviluppo.
Il rettangolo verde sottostante rappresenta lo sviluppo di un cilindro e la linea blu è il tracciato di una strada che si avvita con pendenza costante (tipo scala a chiocciola).
Il disegno color arancio è lo sviluppo del nostro tronco di cono. La linea blu è il tracciato della strada da costruire per salire da A a B. Sul piano la pendenza di questa linea si inerpica sempre più, ma riavvolgendo questo sviluppo a formare il solido, questa apparente ripidità svanisce per effetto della convergenza delle generatrici in direzione del vertice del cono.
E' forse questo il dubbio del giovane geometra?
penso che la situazione sia stata spiegata bene... non ho mai detto che deve essere a pendenza costante... ma che deve avere altre caratteristiche. L'esempio da A ad A è molto indicativo... costruite una strada a fondo valle, oppure anche da B a B e capirete il problema...
e non dimentichiamo ciò che dice il secondo giovane papallicolo...
Ripropongo la figura qualitativa dello sviluppo del tronco di cono e del percorso delle strade.
La strada più breve per andare da A ad A' (il medesimo punto di partenza a cui si torna dopo avere girato attorno al cono) è quella indicata dalla linea verde. Questa linea però non è adagiata sul piano orizzontale, ossia non coincide con la circonferenza di base, ma percorre una ellisse che abbrevia il percorso sfruttando il restringimento del cono.
A questo punto la linea retta che collega A B potrebbe non essere quella più breve? esiste forse una linea che sale oltre il limite del ghiaccio e torna a scendere verso B come la linea nera della figura?
Su ciò che dice il secondo giovane: se la montagna fosse meno ripida probabilmente la lunghezza del percorso sul ghiaccio aumenterebbe, ossia la linea nera si avvicinerebbe di più alla cima.
Penso di avere capito che lo sviluppo del cono debba avere questo aspetto e che la linea retta blu tracciata sul piano per congiungere AB (effettivamente la più breve per unire nello spazio i due punti A e B) attraversa la zona ghiacciata.
L'angolo di apertura del cono sembra essere un elemento cruciale. Se supera un certo valore si invade la zona del ghiaccio
Aggiungerei che, non potendo passare nella zona ghiacciata, la strada meno lunga dovrebbe essere il tratto da A al punto di tangenza con la circonferenza di confine tra le due zone, alla quota di B, e poi l'arco di circonferenza da questo punto fino a B a quota costante, come indicato dal percorso giallo nella figura sottostante:
Ecco, non avevo capito che quando il Papalgeometra suggerisce di fare la prova in piano, si riferisce al piano su cui viene sviluppata la superficie tronco conica tra A e B (un giro completo) . Se è così, e considerato pure che la strada cercata, in effetti, non è a pendenza costante ma la "più breve", è chiaro che qualsiasi segmento di retta congiungente A e B nello sviluppo piano della superficie tronco-conica intersecherà l'arco di circonferenza passante per B, invadendo quindi la zona ghiacciata. Il ragionamento torna anche considerando una traiettoria da A ad A o da B a B, sempre nel piano di sviluppo della superficie tronco-conica. Inoltre, all'aumentare di R, a parità di H del cono , cioè , in pratica , al diminuire della ripidità del cono, il segmento di retta congiungente A e B nel piano suddetto tende ad avvicinarsi sempre di più al vertice del cono.
In definitiva, credo che in questi termini , cioè se si cerca la strada più corta tra A e B compiendo un giro completo attorno all'asse del cono, il Papalgeometra abbia ragione. La strada a pendenza costante secondo un'elica conica non è quella più corta, ma in compenso è realizzabile
Credo ci possano essere 3 casi che dipendono da quanto è ripido il cono.
Se il cono è abbastanza ripido è possibile seguire il percorso più breve senza dover passare sulla zona innevata. Nelle figure sotto c'è il percorso riportato in piano sul cono aperto e come appare sulle pendici del cono.
Se il cono è meno ripido il percorso più corto dovrebbe attraversare la zona innevata ed ad un certo punto invertirebbe la pendenza.
Se il cono è ancora meno ripido, il criterio di seguire la retta sul cono aperto sul piano non funziona più. Credo che l'ultimo personaggio si riferisse a questa situazione.
OH... bene bene... stiamo parlando scherzosamente delle geodetiche (chiuse) di una superficie conica: sono sempre ellissi e non cerchi. Ne segue che a seconda dell'apertura del cono si possono avere diverse possibilità, anche per traiettorie aperte, ma tali da compiere un angolo giro. La cosa migliore è sempre aprire il cono e poi tracciare le linee di minore distanza (rette, fino a che è possibile). In generale, la geodetica sale e poi arriva in B in "discesa", il che vuol dire che deve attraversare la neve... Vale la pena ampliare un poco il quiz, inserendo dei numeri e fare un paio di domande... SEGUIRA' TRA NON MOLTO LA PARTE SECONDA NUMERICA...
Per il "pratico" Arturo... Basta fare un laccio attorno a un cono con uno spago che parta da B e arrivi a B e si vedrà che se descrive un'ellisse si può tendere senza farlo scivolare e sarà più corto di qualsiasi altro tentativo...
Comunque sempre in gamba i "nostri" maghi...
Caro Vincenzo, se trovo il cartoncino farò la prova pratica che mi suggerisci. Intanto ho provato con geogebra (e ti pareva ? :-) ). Nella applicazione di cui al link seguente abbiamo la situazione piana a sinistra e quella solida a destra. Facendo partire l'animazione, osserviamo come cambia sia nel piano sia nello spazio. Purtroppo , nella vista grafica solida si vedono formarsi due geodetiche per come ho ricavato i punti (intersezione in cui cui entra in gioco un piano perpendicolare al piano xy e passante per l'asse del cono , che ruota attorno a tale asse di 360 gradi, all'unisono con la rotazione di una semiretta passante per il vertice visibile nella vista grafica piana. Non è possibile considerare solo un semipiano).
Spero si veda chiaramente che in effetti , nella situazione considerata, la strada invaderebbe la zona del ghiacciaio.
https://ggbm.at/M8BPNNAR
Ottimo come sempre caro Artù! Con le due nuove domande, che aggiungerò nella parte seconda, ti divertirai da matti...
buttata là veloce:
Se si prende lo sviluppo del cono OBAA'B'O
si nota che la strada, non potendo sconfinare in zona ghiaccio e percorrere almeno un giro, deve essere tangente all' arco BB'.
Si vede anche che il triangolo OAB' (ove AB' è la strada più corta in quanto retta geodetica in un pian o euclideo) è equilatero con cateti OB' e B'A e angolo al centro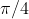
.
Poniamo per comodità l'ipotenusa OA unitaria, il cateto OB' sarà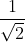
.
La base della montagna AA' sarà quindi data dall'angolo al vertice moltiplicato OA=1 , quindi Base=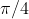
.
Il raggio della montagna è AA' diviso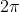
quindi raggio= 
.
Da cui si ricava col teorema di pitagora l'altezza massima possibile della montagna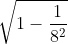
= 
,
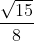ricordando che abbiamo assunto OB = OB' =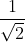
, con facili proporzioni
si ottiene la quota neve relativa =}{8&space;\sqrt{2}})
OK Leandro,
però non capisco per quale motivo il triangolo deve essere per forza equilatero... La distanza AB non è stata fissata e nemmeno l'ampiezza e l'altezza del cono... il tuo mi sembra un caso del tutto particolare...
Comunque, l'analisi va avanti in una seconda puntata e potremo parlarne con maggiore attenzione
caro Leandro...
riguardavo la tua figura e mi sono accorto che tu parli di triangolo equilatero... impossibile. Come può mai essere OB' = OA ?? Forse intendevi solo isoscele, ma anche così non capisco perché lo debba essere...
No, c'è qualcosa che non va...
In attesa della seconda puntata, non disponendo di misure di altezza e diametro di base del cono, possiamo fare solo alcune considerazioni sull'angolo di apertura e sulla ripidità del versante del cono, a seconda delle diverse ipotesi esposte anche nel commento di Fabrizio.
Nel caso che il cono sia molto ripido, è possibile andare da A a B senza invadere la zona del ghiaccio. Volendo esprimere quantitativamente questa condizione possiamo riferirci a questa figura:
ACD rappresenta lo sviluppo del cono e AB il percorso che sale girandogli attorno senza invadere la parte superiore ghiacciata. Nel punto B la retta passante per AB è tangente al cerchio bianco del ghiacciaio.
Il triangolo ABC è rettangolo e il suo cateto BC è metà della ipotenusa, quindi l'angolo ACB è di 60°
L'arco AD ha la lunghezza della circonferenza di base ( il cui raggio è r ) è misura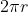
Questa misura corrisponde al valore del lato del cono ( l ) per l'ampiezza dell'angolo ACD (=ACB) in radianti e vale quindi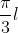
dalla uguaglianza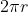
=
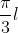ricavo il rapporto 
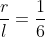che rappresenta il seno dell'angolo di semiapertura del cono. Calcolo quindi )
= 10° circa.
Questo significa che la ripidità del versante della salita è di 80°. Anche compiendo un giro attorno al cono, la pendenza sarebbe eccessiva. Per ottenere una strada percorribile occorrerebbe girare più volte attorno al cono.
Questo caso limite però non corrisponde alla situazione del quiz. la salita lungo la generatrice è meno ripida di 80°, perché sappiamo che dovremo transitare sulla zona ghiacciata e ciò significa che l'angolo dello sviluppo del cono è più ampio.
Il cono quindi non è così ripido e la strada oltrepasserà il confine dove inizia il ghiaccio per poi scendere verso B
Ma il cono non può essere meno ripido di un certo limite, che è quello in cui il suo sviluppo corrisponde all'angolo piatto. Lo illustra bene il commento di Fabrizio (caso 3). Possiamo calcolare la ripidità del versante anche in questo caso.
la circonferenza misura, come sappiamo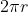
e questa misura, espressa in funzione di l, vale ora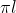 
dalla uguaglianza, come prima, ricavo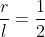
e )
= 30° Quindi la ripidità della salita è di 60°.
Si tratta comunque di una pendenza elevata per la strada che ora ci conduce direttamente a B lungo la generatrice del cono.
A ben vedere, in questo caso limite, non vi è un reale "giro" intorno al cono, in quanto da A si arriva alla vetta e poi si discende verso B sullo stesso tracciato in direzione opposta. A questo punto è del tutto inutile salire fino in cima perché già all'andata si passa per B. Quindi si evita il ghiaccio, si riduce la strada alla sola salita da A a B ma la pendenza resta molto elevata.
L' unica informazione quantitativa che siamo riusciti a dedurre è quindi che la ripidità della salita è inferiore a 80° (dal commento del giovane papalgeometra) e superiore a 60°(dal secondo commento espresso dal passante)
caro Mau... molte cose le ritrovi nelle domande della seconda parte...
Non mettiamo però limiti alle papallauto! Non possono ovviamente andare in modo diretto d A a B, ma un giro attorno al monte lo fanno sempre... Il papallasfalto riesce a tenere ancorate le ruote anche se girano (tecnologie d'avanguardia). Però, come vediamo, non amano il ghiaccio...
Mettiamo i prossimi commenti nel nuovo articolo che è apparso in evidenza...