Categorie: Matematica
Tags: curvatura estrinseca geodetiche geometria Papalla quiz soluzione superficie conica
Scritto da: Vincenzo Zappalà
Commenti:20
Il quasi-quiz del Monte Cono. Seconda parte **
Nella prima parte del quasi-quiz sul Monte Cono di Papalla, volevamo solo mettere l’accento su quali siano le geodetiche di una superficie conica. Pur essendo estremamente semplici da identificare, possono creare una qualche confusione passando all’atto pratico. Chiariamo bene la loro struttura (rispondendo al quiz) e passiamo a qualche calcolo di minima difficoltà, ma di indubbio interesse.
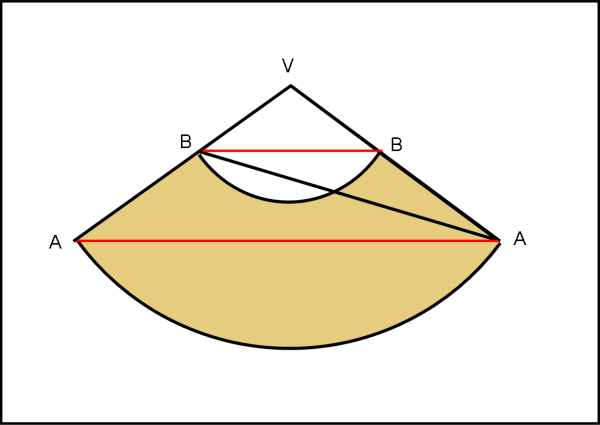
Ricordiamoci, innanzitutto, che una superficie conica è una superficie curva in senso estrinseco. Le sue geodetiche sono linee a curvatura nulla e per notare ciò basta “aprire” in nostro Monte Cono secondo una generatrice (ad esempio proprio quella che contiene sia A che B) e ragionarci sopra per un attimo. Ormai ci siamo trasportati su un piano ed è immediato trovare la linea di minima distanza tra due punti della stessa generatrice, escludendo il percorso (troppo ripido) che si svolge proprio lungo la generatrice. La geodetica tra A e B non è altro che il segmento rettilineo che li unisce.
Particolarmente interessante per comprendere come questo segmento si trasformi ricostruendo il cono è considerare il punto A coincidente con B. Lo stesso risultato si ha prendendo il punto a qualsiasi altezza, anche al livello più basso, com’è, in effetti, il nostro punto di partenza della vecchia funivia (A). A prima vista, molti direbbero: “Facile! E’ la circonferenza che forma la base del cono”. E, invece no, dato che la minima distanza (riportata nel piano della figura) è il segmento AA ben più corto della circonferenza di base. Si vede chiaramente che questo segmento si allontana gradatamente dalla circonferenza di base e poi torna ad avvicinarsi fino a incontrarla nel punto di arrivo (che è anche quello di partenza).
Visto dal di fuori, nelle tre dimensioni, il segmento parte da A si alza lungo la superficie del cono e ritorna a scendere, descrivendo una curva. Quale sia questa curva è facile dedurlo, dato che siamo proprio su un … cono. Essa è una ellisse tale da unire A con A secondo un percorso decisamente più corto di quanto non sia la circonferenza di base. La stessa cosa si ottiene partendo da un punto A e finendo a un punto B più alto. La curva, non più un’ellisse chiusa, deve comunque salire, facilmente, più in alto del punto di arrivo e poi scendere fino a incontrare B. Ne segue che durante il tratto più alto di B, la strada più corta ha grande facilità di attraversare la zona innevata.
Facciamo un caso pratico.
Raggio di base, R = 20
Apotema del cono, a = 60
Distanza tra A e B, lungo l’apotema, AB = d = 10
1a) Determinare la lunghezza di tutta la strada di minima distanza costruita su un monte reale.
1b) Determinare la lunghezza del suo tratto in discesa.
1c) E’ possibile determinare facilmente i semiassi dell’ellisse percorsa per una strada di minimo percorso tra B e B?
Più in generale (per un cono qualsiasi) rispondere alle seguenti domande:
2) Vi è la possibilità di avere una strada di minimo percorso da A a B che non attraversi la neve? In altre parole, qual è la condizione limite per cui il percorso di minima distanza tra A e B continui a crescere e non scenda mai?
3) Esiste un’apertura limite del cono (angolo al vertice V, tra altezza e apotema) per cui non esiste la possibilità di costruire la strada di minimo percorso tra A e A, o tra B e B o tra A e B (questa parte si riferisce al problema posto dal secondo giovane papallo nella prima parte del quiz)
Alla fine la superficie conica non avrà più segreti per noi e potremmo anche riuscire a viverci…
Se vi vengono altre idee in testa, dateci pure dentro.
QUI la soluzione di tutti i quesiti tranne il 1c
QUI la soluzione del quesito 1c
Vi è piaciuto calcolare questo percorso? QUI ne troverete altri!
20 commenti
Lascio, almeno per il momento, spazio ai lettori che desiderano dare risposta alle nuove domande, ma ne vorrei aggiungere una alla numero 3.
Esiste un valore dell'angolo di apertura del cono oltre il quale non è più possibile costruire un percorso che vada da A a B girando intorno al cono. Ma un percorso che vada da A a B di lunghezza minima esiste ed è proprio lungo la generatrice. Tuttavia la pendenza lungo questa "direttissima" potrebbe non essere superabile dai mezzi a disposizione. In altre parole, se stabiliamo una pendenza massima che i veicoli possono affrontare e la confrontiamo con la ripidità della generatrice abbiamo il problema di trovare il percorso minimo "condizionato" dal valore della pendenza massima affrontabile. E' un problema molto concreto che trova soluzione nella configurazione a tornanti che vediamo sulle nostre montagne. Ma come segmentare i tratti a zig zag che consentono di arrivare al traguardo, realizzando la strada più corta senza mai superare la pendenza limite affrontabile dai mezzi?
Il problema sollevato è decisamente molto pratico e realistico. Ben vengano i tornanti... tuttavia, in America (nella zona dei vulcani dell'Oregon e del nord della California) vi sono anche strade che girano attorno al monte proprio spiraleggiando. Non geodetiche, ma curve con più rotazioni, facili da disegnare.... Guarda te un semplice cono quante belle cose ci insegna...
La mia risposta parziale alle domande è questa. Forze l'ho fatta più complicata di quella che potrebbe essere. Infatti non ho trovato una risposta semplice alla domanda 1c.
Per comodità chiamo in questo modo queste lunghezze ed angoli
La lunghezza dell'arco di raggio a nel cono aperto deve essere uguale all'intera circonferenza di base del cono, quindi:
1a) La minima distanza è c nel triangolo BVA. La trovo con il teorema di Carnot
1b) il tratto in discesa va dal punto di minima distanza da V del segmento AB fino a B. Questo punto di minima distanza, H, è il piede dell'altezza del triangolo AVB sul lato AB. Il valore di VH ottenuto dal teorema di Pitagora applicato al triangolo BVH e AVH deve essere lo stesso. Da questa uguaglianza si può ottenere la lunghezza di BH
2) la condizione limite per il passaggio sulla neve del percorso di minima distanza è quando l'angolo AB e BV sono perpendicolari. Un modo per ottenere questa condizione è imporre la lunghezza di BH=0 nella formula sopra.
3) se l'angolo AVB supera i 180°, il segmento AB non è più sul cono. Quindi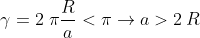
Vale a dire che l'angolo limite tra altezza ed apotema del cono è 30°
La risposta alla domanda di Maurizio mi viene anche più complicata. Per il momento la lascio in sospeso.
Per la domanda 1c, ho provato a studiare la situazione, probabilmente complicandola
Allego la vista piana del solido aperto e quella solida del cono nello spazio.
L'ellisse di minimo percorso passa sicuramente per B e per il punto H. Questo punto è quello a metà strada , in corrispondenza del quale si smette di salire e si comincia a ridiscendere verso B. La lunghezza del segmento VH la calcoliamo facilmente nella vista piana (l'angolo al vertice V è di 120°, quindi l'angolo BVH è di 60°, del segmento BV pure calcoliamo facilmente la lunghezza, pari all'apotema AV del cono meno la distanza AB). Da facili considerazioni geometriche, nella vista solida mi ricavo le coordinate spaziali del punto H. La distanza BH è l'asse maggiore dell'ellisse. B ed H giacciono sullo stesso piano (y=0), per cui la loro distanza è facilmente calcolabile con la formula di geometria analitica della distanza tra due punti nel piano, sapendone le coordinate. Nella vista piana, inoltre, la lunghezza del segmento BB altro non è che il perimetro dell'ellisse di minimo percorso. Conoscendo il perimetro dell'ellisse e il suo asse maggiore , posso ricavarmi quello minore dalla formula (approssimata) del perimetro dell'ellisse
essendo a e b i due semiassi dell'ellisse.
Nel caso in questione, verrebbe a = 17,18 e b=9,21
caro Arturo... per trovare b, io direi che dovrebbe riferirsi al punto di mezzo tra H e B e uguale al raggio della sezione circolare in quel punto... o sbaglio?
Il raggio (evidenziato in rosso nella seguente figura) della circonferenza ottenuta sezionando il cono con un piano parallelo al piano xy e passante per il punto di mezzo di BH è pari a 12,5, contro i 9,21 del semiasse minore calcolato prima ed evidenziato in blu nella figura.
Forse mi sbaglio... ma non mi torna la figura, il tratto rosso non dovrebbe coincidere con il tratto blu? L'ellisse dovrebbe essere posta simmetricamente rispetto all'asse... ma potrei sbagliarmi, dato che non ho ancora fatto calcoli...
Ho impostato la soluzione in questo modo:
AA' = 40
AV=A'V= 60
AB=A'B'= 10
Uguagliando l'arco dello sviluppo del cono alla sua circonferenza di base, si ricava facilmente l'angolo BVB' che vale 120°
Di conseguenza, sullo sviluppo, VH vale metà di VB, ossia 25 e HP vale 60-25 = 35
Sul cono la distanza HA' vale 35 e la distanza HB' vale 35-10 = 25
L'asse maggiore della ellisse, osservando il cono solido la si vede di taglio, è BH e vale
BB' vale 5/6 di AA' = 5/6*40 = 33,33
DB' vale 1/3 di HB' = 1/3* 25 = 8,33
radice di 8/9 vale 0,94
Sostituendo i valori otteniamo:
Il semiasse maggiore, "a" vale quindi 17,15
Per quanto riguarda il semiasse minore considero che il punto O, centrale per l'ellisse, si trova sul cerchio a quota CC', il cui diametro vale AA'*VC'/VA' che in numeri significa:
40*(37,5/60) = 25. Questo cerchio ha centro in K e raggio pari a 12,5.
Ribaltandolo frontalmente, come se lo osservassimo dall'alto, vediamo il segmento OT che è proprio il semiasse minore, "b".
Non resta che calcolare il suo valore. Osserviamo che la distanza OK vale 1/3*HC' = 4,17.
Abbiamo già valutato KT, raggio del cerchio, pari a 12,5 non resta che calcolare il valore del cateto OT
OT=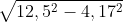
= 11,77
Quindi la misura del semiasse minore "b" della ellisse è 11,77
L'ellisse visibile nella figura è stata ottenuta sezionando il cono con un piano passante per B (dato), H (ricavato dai dati) e perpendicolare al piano xz (a cui appartengono i punti B ed H). Confrontando costruzione solida e conti fatti a mano, mi trovo con tutto, tranne che con la misura del semiasse minore dell'ellisse. Né penso che l'approssimazione della formula del perimetro dell'ellisse sia tale da indurre quella differenza tra i 9,21 calcolati e gli 11,78 misurati. Bisogna indagare ...
mi sembra che la costruzione sia giusta...
Ciao Arturo, prova a confrontare il tuo ragionamento con la soluzione che ho appena postato, magari si trova una spiegazione per la discrepanza sul valore del semiasse minore. Nel frattempo analizzo la tua figura.
Sapevo che la formula del perimetro della ellisse fornisce un valore approssimato per eccesso del reale perimetro, quindi ricavando il semiasse minore si dovrebbe avere un valore approssimato per difetto. Non mi aspettavo invece che l'errore della approssimazione fosse così grossolano. Si tratta di 9,21 contr o 11,78, ossia -2,57/11,78 pari a quasi il 22% in meno. (potrebbe esserci una evasione dell' l'IVA ?)
Non è che viene fuori un quiz nel quiz ?
Ho provato a usare per la lunghezza del perimetro di una ellisse la formula più precisa , ossia
2p= 4*a*E(e)
dove E(e) è un integrale ellittico completo di seconda specie... il cui sviluppo in serie porta ad una formula della lunghezza dell'ellisse sicuramente più precisa di quella comunemente nota. Ma anche così, con i valori dei due semiassi trovati anche da Maurizio , ottengo per la lunghezza dell'ellisse un valore sui 92, contro 86,6 che è il dato immediatamente ricavabile aprendo sul piano il cono.
Quindi, passando dalla formula meno approssimata, che con i valori di semiassi che abbiamo calcolato, fornisce un perimetro di 94,6 alla formula più precisa con il calcolo dell'integrale, scendiamo a 92, un valore ancora ben lontano da quell' 86,6 , ottenuto immediatamente, che sembrerebbe indiscutibile.
Sul semiasse maggiore non vedo possibili errori. Ma anche i ragionamenti per trovare il semiasse minore mi sembrano validi. Possibile che i risultati delle formule siano così approssimativi?
Con a=17,18 e b=11,78 con la formula nota del perimetro ottengo 92,55, valore non lontano da quello ottenuto con la formula piu' precisa (e sviluppo in serie fermato a terzo termine). Quindi non penso sia una questione di maggiore o minore approssimazione. E neppure mi pare sia errato il ragionamento seguito, visto che i risultati combaciano. Aspetto la soluzione del nostro caro Vincenzo.
ma che mi venisse un colpo....
(qui si vede la geodetica da A ad A, ma anche se fosse da B a B non cambierebbe forma...)
Ho provato a rifare il calcolo della lunghezza dell'asse minore sfruttando la figura del cono 3D di Arturo che mi ha fatto capire come si colloca il semiasse minore.
Parto da una considerazione sul cono aperto che spero sia valida. L'ellisse è divisa dagli assi in 4 parti uguali. Allora il punto T nel cono aperto si trova a metà tra B ed H.
L'angolo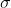 
non è 1/4 del totale, ma occorre calcolarlo tramite la sua tangente.
di conseguenza}{\cos(\sigma&space;)}\simeq&space;33)
Il raggio del cono al livello dell'asse minore è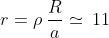
Arturo mi ha fatto notare che questo raggio non è il semiasse minore perché nel punto T non è a 90° rispetto al punto B. L'anticipo rispetto a 90° è
Quindi il\simeq\:9,28)
Il risultato è molto vicino a uno dei due indicati da Arturo. La differenza potrebbe essere dovuta alle approssimazioni.
Prima di inviare il mio commento precedente non avevo visto l'ultima figura di Arturo.
La geodetica nella figura di Arturo non sembrerebbe essere una curva piana.
In effetti, riferendomi alla figura del mio commento sopra, se la geodetica fosse un ellisse ρ dovrebbe avere un valore intermedio tra b e VH, ma non è così.
NOTA BENE
cari amici,
potrei fare il "furbetto" del quartierino e dire: "volevo cercare di ingannarvi con l'ellisse". E, invece, no. Non mi vergogno ad ammettere che mi ero convinto a priori che la geodetica (rettilinea) dovesse trasformarsi in ellisse sul cono in 3d. La mia "presunzione" si è scaricata sui tre maghi Mau, Artù e Fabry che, però, un po' alla volta, hanno svelato la mia involontaria avventatezza... Esiste sicuramente un'ellisse che ha un percorso minore di quella cel cerchio orizzontale, ma questa non è la geodetica. La geodetica si trasforma in 3d in qualche cosa di diverso da un'ellisse. I maghi ci stanno lavorando sopra e la soluzione riporterà il risultato (con qualche considerazione psicologica).
Sospendiamo, perciò, la domanda 1c, anche se esiste in realtà un'ellisse di minimo percorso che però non è la geodetica del cono.
Fatemi dire che questo circolo è fantastico (grazie ai lettori, soprattutto se sono maghi...): anche da "errori" miei si riesce a trovare qualcosa di nuovo e stimolante. Ora il cono comincia a non avere più segreti realmente!!!!
E' bello sbagliare se serve a imparare!!!!
Uguaglio le due equazioni
ponendo per comodità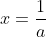
La prima espressione è la funzione coseno che deve uguagliare una retta con pendenza negativa passante per 1.
Ci sono casi in cui la retta interseca la funzione in più punti ma esiste una soluzione (doppia) in cui la retta è tangente alla funzione coseno
Valori di d superiori al limite imposto non daranno luogo a soluzioni e quindi non esisteranno geodetiche soddisfacenti i requisiti imposti.
Uguagliando le dirivate nel punto di tangenza si ottiene la relazione limite tra R, a e d:
E' subito evidente, per le proprietà della funzione seno, che d deve essere minore della circonferenza alla base del cono.