(Questa soluzione si basa sui contributi congiunti di  Arturo, Fabrizio e Maurizio).

Dopo le soluzioni ai quesiti "semplici" elaborate da Vincenzo e Fabrizio (QUI), eccoci finalmente a discutere della insidiosa domanda 1C, contenuta nella seconda parte del  quasi-quiz sul Monte Cono.

Sembrava che il quiz consistesse nel determinare dei semiassi, invece...

 

La domanda era questa:

1c) E’ possibile determinare facilmente i semiassi dell’ellisse percorsa per una strada di minimo percorso tra B e B?

La insidia maggiore sta proprio nella parola "ellisse", dato che la curva di minimo percorso non ha la struttura di una ellisse, come vedremo.

 

Pensandoci su...

In un interessante ebook che tratta della geometria su sfera , cilindro, cono e pseudosfera, acquistabile in rete, viene citato Seymour Papert, matematico, informatico e pedagogista, scomparso nel 2016, il quale sosteneva che : “Impariamo meglio facendo, impariamo ancora meglio se colleghiamo il nostro fare con il parlare ed il pensare su ciò che abbiamo fatto”.

Papert introduce il concetto di costruzionismo nelle teorie dell'apprendimento, la necessità di realizzare artefatti cognitivi, ovvero oggetti e dispositivi che facilitano lo sviluppo di specifici apprendimenti.

Nelle didattiche proposte da Papert, ha grande importanza la gestione dell'errore: la sua idea è che l'unica via per imparare in modo significativo, sia quella di prendere coscienza dei propri errori.

Personalmente (Maurizio) sono convinto che, anche quando non si commettono errori, sarebbe bene fermarsi a riflettere sul "perché non abbiamo sbagliato".

Ma è più difficile soffermarsi ad analizzare le ragioni di una vittoria che quelle di una sconfitta.

Veniamo ora al nostro problema della geodetica ( la linea di lunghezza minima che congiunge due punti di una superficie e giace sulla superficie stessa)  sul cono.

Adesso sappiamo (e lo vedremo in dettaglio tra poco ) che il cammino più breve che unisce un punto a se stesso, girando attorno al cono non è una ellisse, ma una curva del tutto dissimile, con una cuspide e una curvatura nello spazio che la discosta dalla superficie del piano con cui possiamo generare ellissi, tagliando il cono.

Ma per quale motivo abbiamo inizialmente dato per scontato che la geodetica fosse una ellisse?

Rileggendo il testo del quiz, troviamo che la domanda 1C chiede di determinare in modo semplice i semiassi di questa ellisse, minimo cammino sul cono per collegare il punto a se stesso.

Ma ancora prima, andando a rileggere i commenti al quiz precedente, propedeutico, ritroviamo precise affermazioni, da parte mia e di Vincenzo, non contrastate da commenti di altri, sul fatto che la curva cercata debba essere una ellisse, ottenuta tagliando il cono con un piano inclinato.

Naturalmente una convinzione condivisa e riaffermata da una fonte attendibile "diventa" ufficialmente la realtà e non viene più messa in discussione.

In questo, dobbiamo riconoscerlo, ci siamo discostati dal metodo Galileiano e ne abbiamo subito le conseguenze.

Eppure sarebbe bastato costruire fisicamente il manufatto (come raccomanda Papert) per rendersi conto del malinteso. Quelle che seguono sono , infatti, le foto di un modello fisico del cono da me realizzato con del cartoncino in un secondo momento. La prima raffigura la superficie laterale del cono compresa tra la sua base e la geodetica, così come si vede nello spazio.

La seconda figura e la terza mostrano la stessa superficie conica come visibile guardandola da altre due angolature nello spazio, per evidenziare l'andamento della geodetica.

 

 

 

 

 

 

 

 

 

 

 

 

La causa prima dell'errore è probabilmente da collegare al fatto che sullo sviluppo piano del cono la geodetica appare semplicemente come il segmento rettilineo che conosciamo. Lo vediamo tangibilmente in questa foto di Figura n,3 bis

Questa linearità è stata indebitamente trasferita nello spazio 3D, associandola ad un piano che interseca il cono. Ma studiando lo sviluppo di una intersezione piano-cono, come faremo più avanti in questo articolo, vedremo che l'ellisse ottenuta, quando la riportiamo sullo sviluppo in piano, non si svolge su un segmento, bensì su una curva ondulata, come si vede chiaramente nella seguente figura n.4. Essa rappresenta lo sviluppo piano del cono, con il segmento di retta AB , di colore blu, che rappresenta lo sviluppo piano della geodetica e la linea curva (di colore giallo) che rappresenta lo sviluppo piano dell'ellisse passante per B ed H. Si nota subito che la lunghezza della linea curva è ben maggiore di quella del segmento AB. Dunque l'ellisse non può essere la geodetica.

 

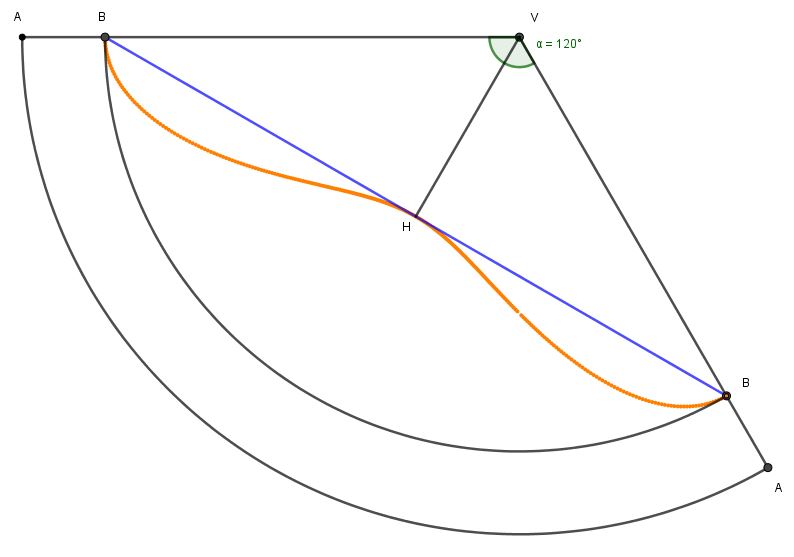
Come è stato scoperto l'errore?

Direi in modo fortuito. Infatti, dopo avere ricavato il presunto "asse maggiore della ellisse", Arturo ha pensato di abbreviare il calcolo per trovare l'altro asse, quello minore, sfruttando la conoscenza del perimetro della ellisse. Per una via diversa, come si può vedere nei commenti al quiz, ragionando sul cono tridimensionale, e anche misurando direttamente il semiasse nella costruzione 3D realizzata da Arturo, si è però giunti ad un diverso valore del semiasse minore, una differenza troppo grande, non giustificabile con le approssimazioni delle formule. Per cui, se la geodetica non ha le misure compatibili con una ellisse, significa che non è una ellisse.

Da qui l'interrogativo: allora cosa è ?

Per quanto mi riguarda ho deciso di guardare in faccia il nemico, disegnando, ritagliando e incollando il cono del mistero, di cui poi ho fatto le foto riprodotte nelle precedenti figure n. 1 , n.2 e n.3. Arturo, da parte sua, vista la discrepanza riscontrata tra misura e calcolo del semiasse minore dell'ellisse, ha cercato anche in rete informazioni sulle geodetiche chiuse sul cono, scoprendo l'ebook citato all'inizio, in cui si parla di questa curva, e poi si è scatenato con geogebra fino allo sfinimento, istigato, ovviamente, dal Maestro.

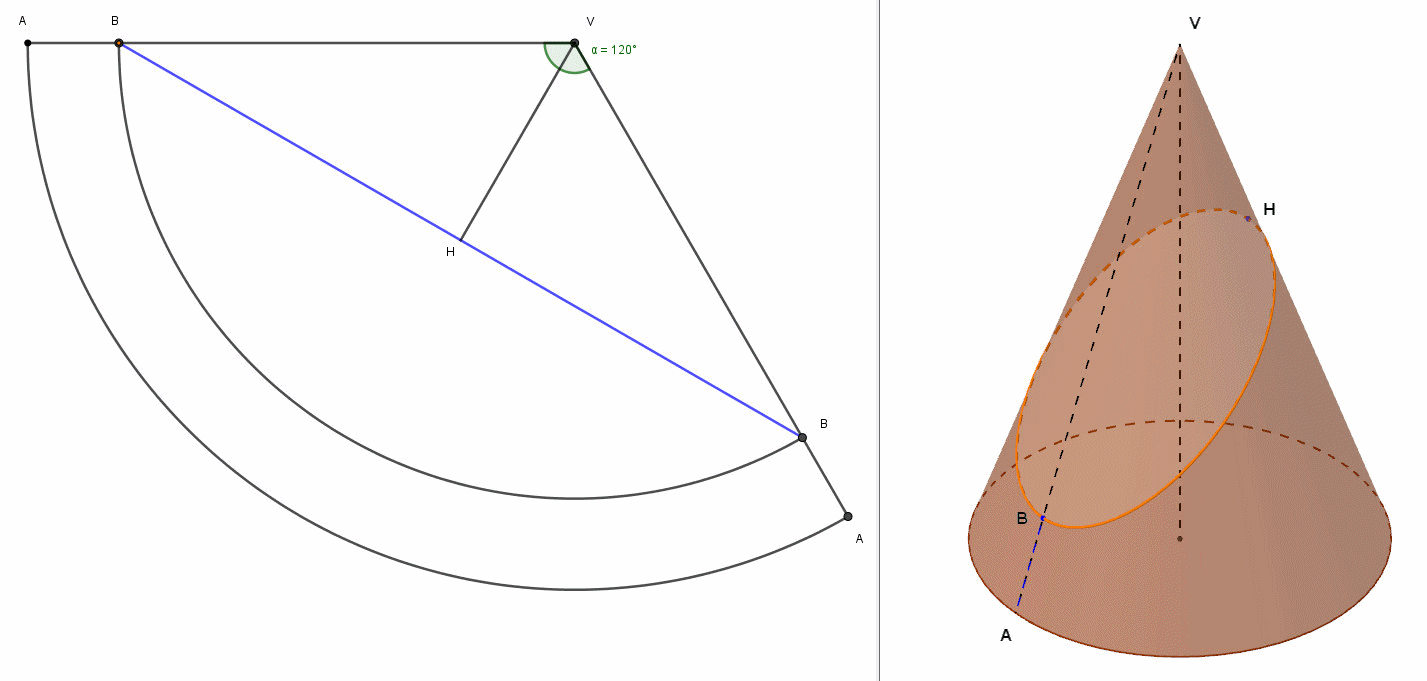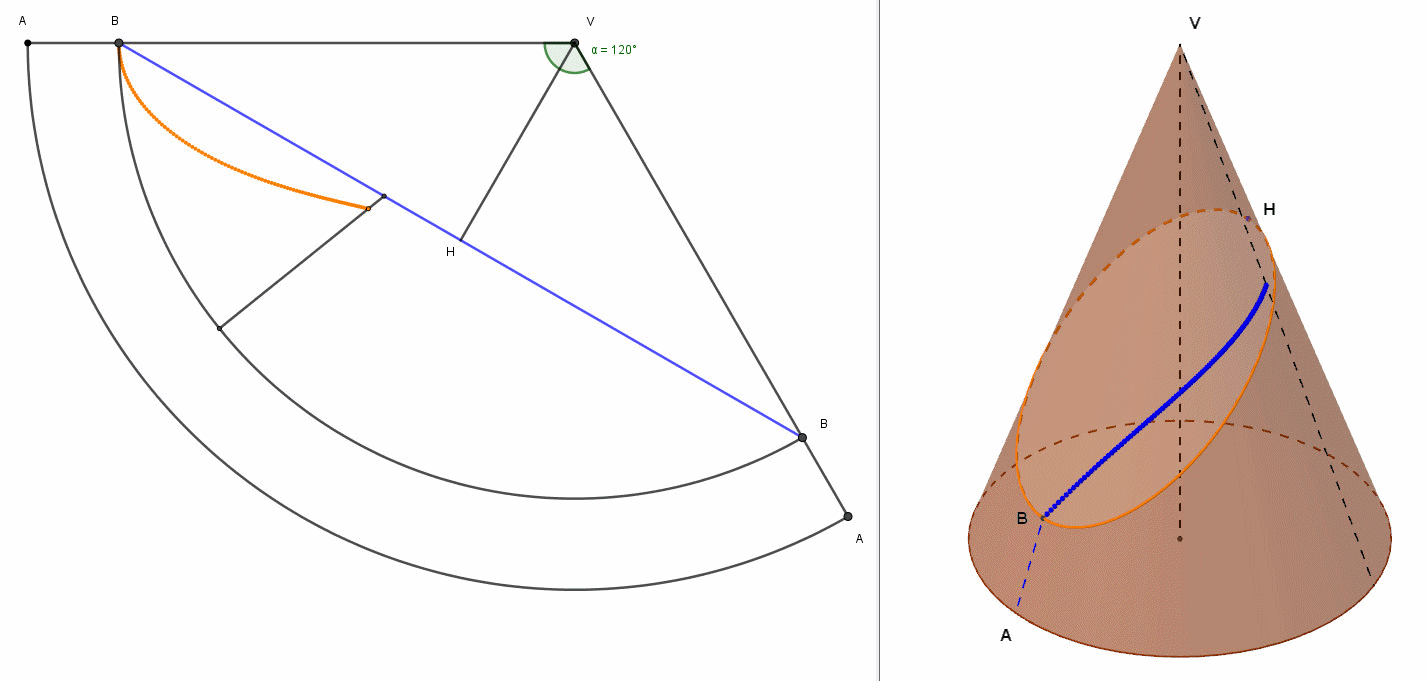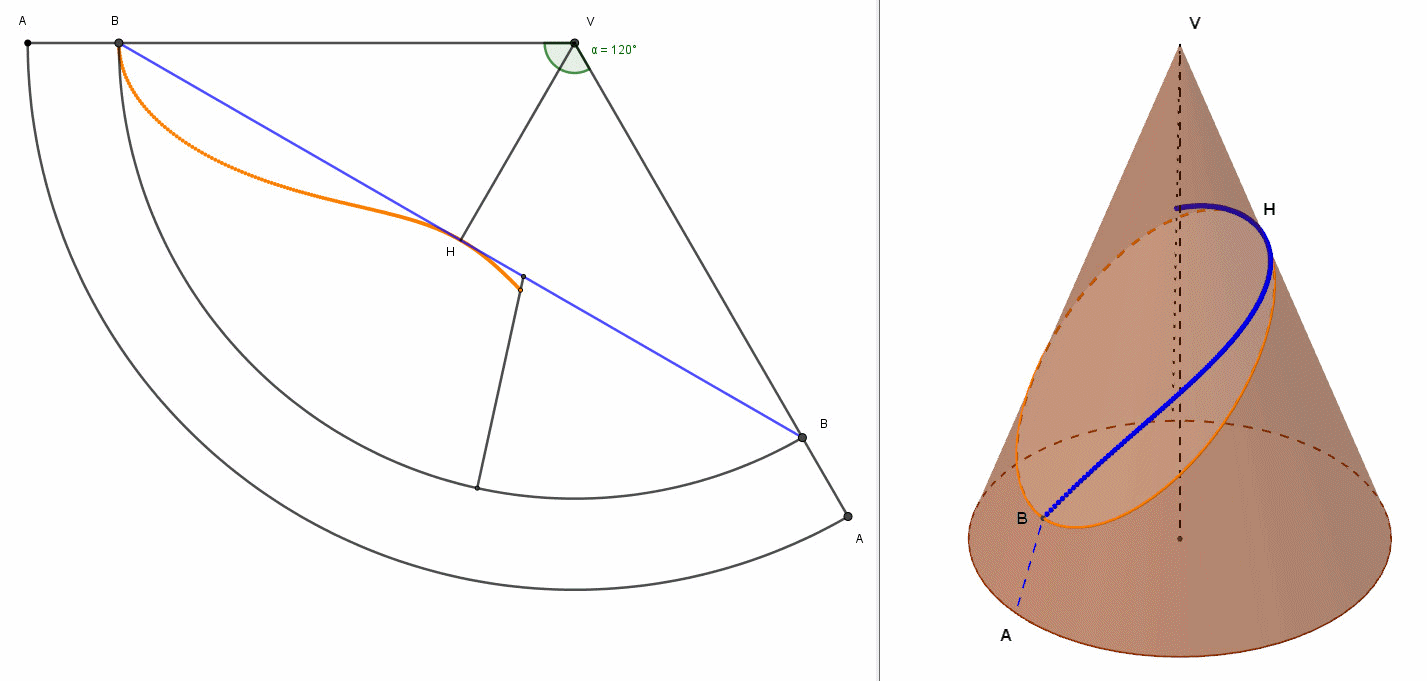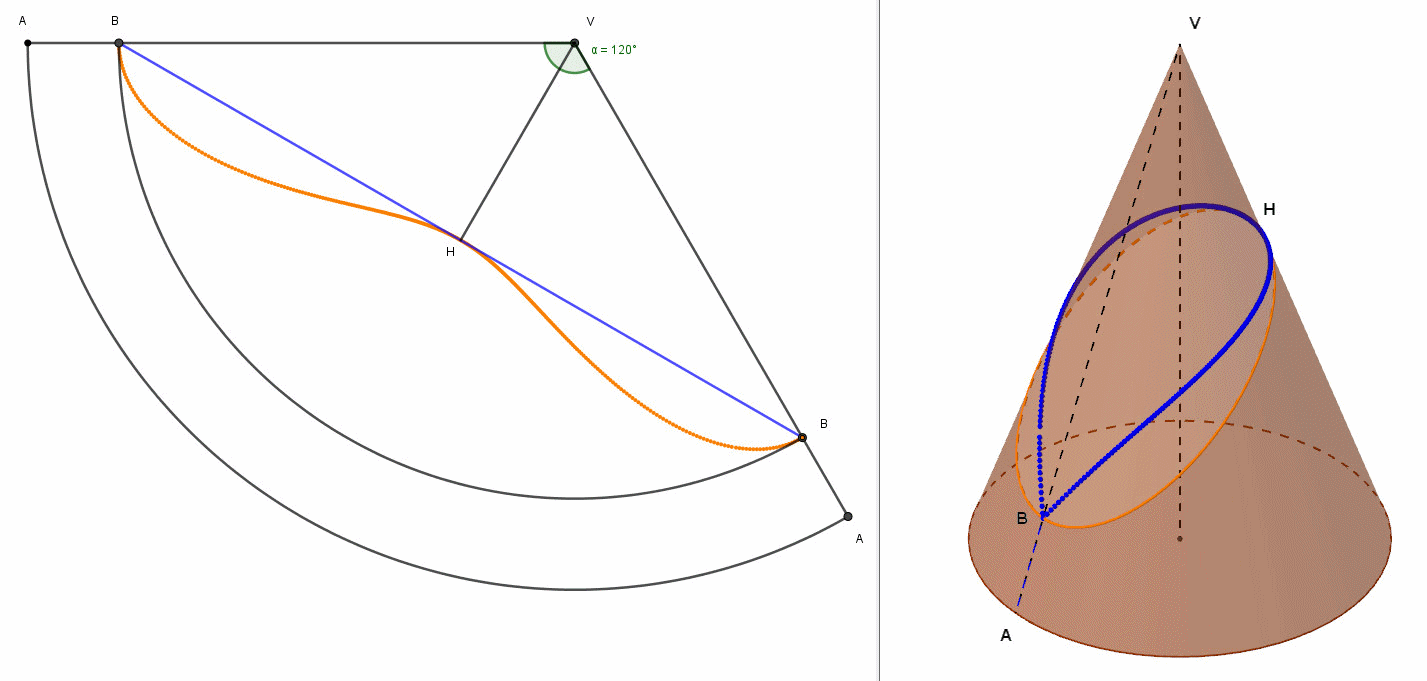
A questo proposito, ha realizzato con geogebra il modello geometrico del cono sia nello spazio che nel suo sviluppo piano, ricavando per punti la linea geodetica  chiusa che parte da B ed arriva in B. Il risultato del suo lavoro è la seguente animazione.

Figura n.5

In tale animazione abbiamo a sinistra la vista dello sviluppo in piano e a destra la vista  in 3D. Nella vista piana osserviamo , stavolta in modo dinamico, il formarsi, per punti, della curva (di colore giallo) equivalente all'ellisse, mentre il segmento blu BH è la  geodetica. Nella vista 3D, invece, vediamo formarsi, sempre per punti, la  geodetica, di colore blu, sovrapposta all'ellisse passante per B e per H. Si nota in tutta la sua evidenza la differenza tra geodetica ed ellisse passante per B ed H.

Seguendo questo link, invece, potete vedere l'animazione in grande, direttamente sul server di Geogebra. In tal modo, potete manipolare la vista 3d, cercando di osservare le curve da diversi punti di vista.

Inoltre, Fabrizio ha determinato analiticamente l'equazione della geodetica. Fabrizio ha affrontato il problema ricorrendo ad una parametrizzazione in coordinate sferiche e coordinate polari con i vantaggi di questa impostazione.

Come si è capito, se tagliamo il cono lungo una generatrice possiamo aprirlo e stenderlo su un piano. Otteniamo così due rappresentazioni della superficie del cono. Quella del cono in 3D e quella della superficie del cono aperta su un piano. In queste due rappresentazioni del cono sono conservate le distanze. La lunghezza di un percorso tracciato sulla superficie del cono 3D è la stessa della traccia dello percorso corrispondente  nella rappresentazione del cono in piano. Intuitivamente questo è vero perché per passare dalla superficie in 3D a quella in piano non è necessario "stiracchiare" nessuna parte del cono. Per una dimostrazione analitica andrebbero confrontate le distanze elementari sulle due superfici e si arriverebbe alla stessa conclusione.

Se quello che ci interessa dei percorsi sono le loro lunghezze, come quando vogliamo tracciare una geodetica, allora possiamo iniziare dalla rappresentazione dove il problema è più semplice e poi convertire il percorso nell'altra.

La conversione è semplice se espressa in coordinate sferiche per il 3D e polari per lo sviluppo in piano.

Nella figura si vedono cosa rappresentano queste coordinate.

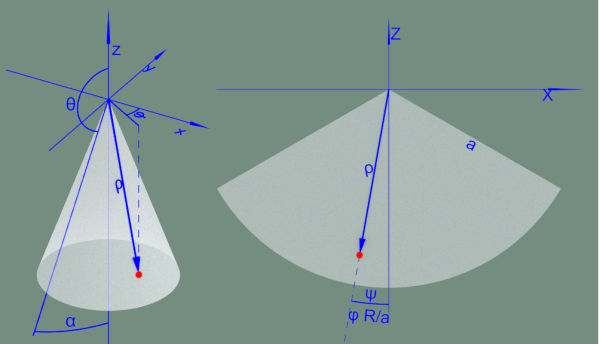
Vediamo quali sono le coordinate di un punto del cono nelle due rappresentazioni. Ho posizionato il cono con il vertice nell'origine e con l'asse verticale.

Un punto generico sulla superficie del cono ha coordinate [ρ,φ,π-α]. La terza coordinata, , ha un valore costante poiché è fissata dall'angolo di apertura del cono, 2α. Le altre due dipendono dalla posizione del punto e le lasciamo generiche. Le corrispondenti coordinate nella rappresentazione 2D si ricavano direttamente come [ρ,φ sin(α)]. Nel nostro quiz sin(α)=R/a. In pratica l'azimut del punto è "compresso" in modo che l'arco di base nella rappresentazione 2D, che è di raggio a, sia lungo come la circonferenza di base del cono di raggio R.

Quindi le coordinate del punto A che nella rappresentazione 3D sono [ρ_A,-π,π-α]= [a,-π,π-α] nella rappresentazione 2D diventano [a,-π R/a]. Analogamente quelle del punto B in 3D sono [b,π,π-α] e in 2D sono [b,π R/a]. Notate che la seconda coordinata  indicano la stessa posizione. Gli ho dato questi due valori perchè cerchiamo una traiettoria che faccia un giro intorno al vertice del cono.

Per costruire la geodetica si può partire dalla sua espressione nella rappresentazione del cono aperto su un piano. In questa rappresentazione piana la geodetica è una retta. Intuitivamente perché è la via più breve tra due punti.

Se vogliamo trovare la geodetica tra i punti A e B dobbiamo trovare l'espressione della retta che passa tra questi due punti. In coordinate cartesiane è

Utilizzo le lettere maiuscole per le coordinate cartesiane della rappresentazione 2D.

Semplice, ma a noi ci serve in coordinate polari. Dobbiamo convertirle sostituendo le X e le Y con i loro equivalenti in coordinate polari ρ sin(ψ) e ρ cos(ψ). Il tutto diventa

.

Utilizzando le denominazioni date nel quiz abbiamo

Gli angoli sono scelti in modo da avere un percorso che faccia un giro completo attorno al vertice.

Ricordando anche che .

Con qualche passaggio (noioso) possiamo trovare la relazione che lega ρ e ψ dei punti di una retta, che è poi l'equazione della retta in coordinate polari, cioè nella rappresentazione 2D:

Per passare alla rappresentazione 3D sappiamo che  è lo stesso e 

che lega due delle tre coordinate. Abbiamo visto sopra che l'altra coordinata ha il valore costante  poiché è fissata dall'angolo di apertura del cono, 2α.

Nel caso delle geodetica chiusa passante per B, oggetto della domanda 1c del quiz, basterà far coincidere le coordinate di A con quelle di B giungendo così alle equazioni in coordinate sferiche della geodetica cercata:

Una volta toccato con mano (nel mio caso) e constatato con geogebra (nel caso di Arturo) che la geodetica cercata non è un'ellisse,  determinatane analiticamente (nel caso di Fabrizio) l'equazione, ci si è chiesti: ma, eventualmente, l'ellisse passante per i punti B ed H della geodetica è almeno l'ellisse di minima lunghezza ?

A questo proposito, esiste sicuramente , tra le infinite ellissi che possiamo tracciare sul cono per girargli attorno partendo e tornando al punto B, quella che ha il perimetro minimo.

Le possiamo vedere tutte, queste ellissi, nella animazione di Arturo:

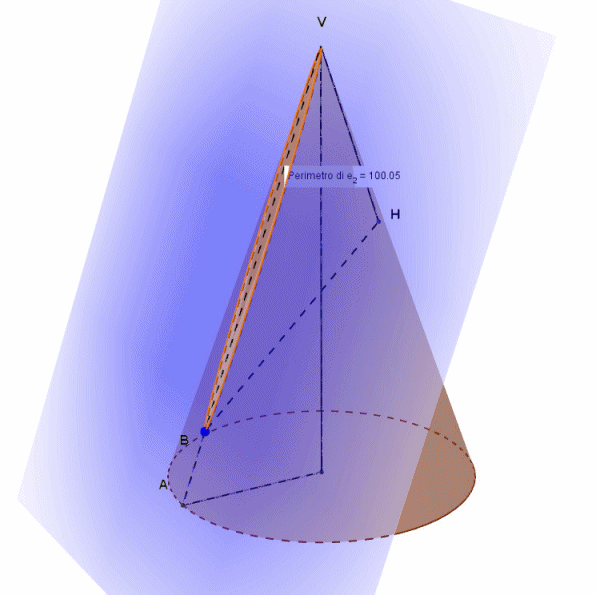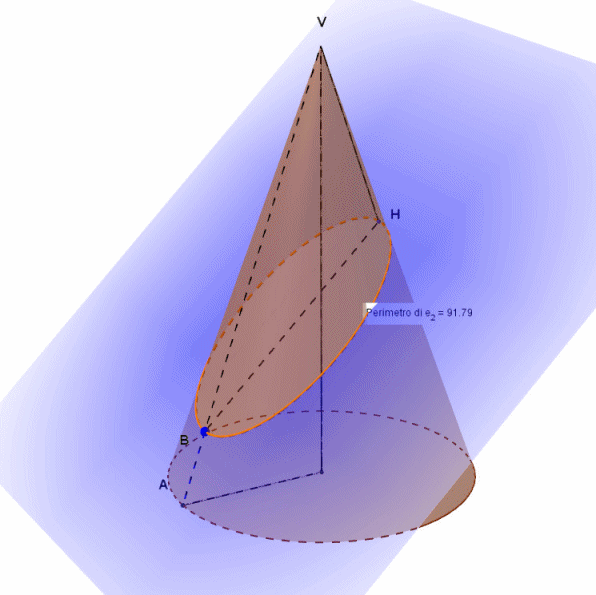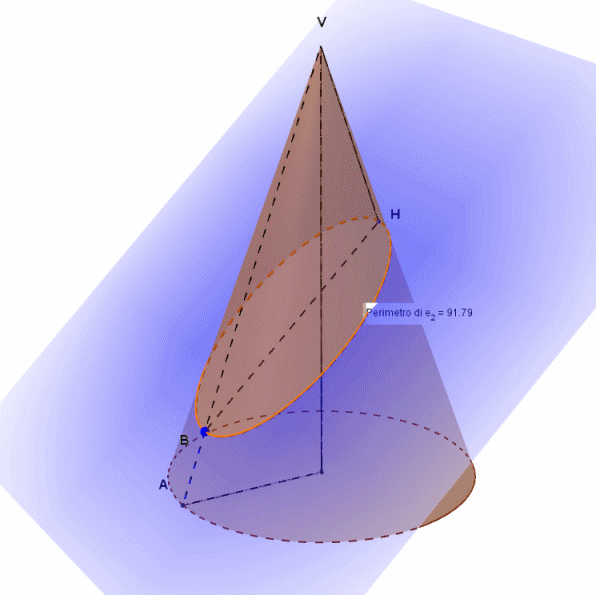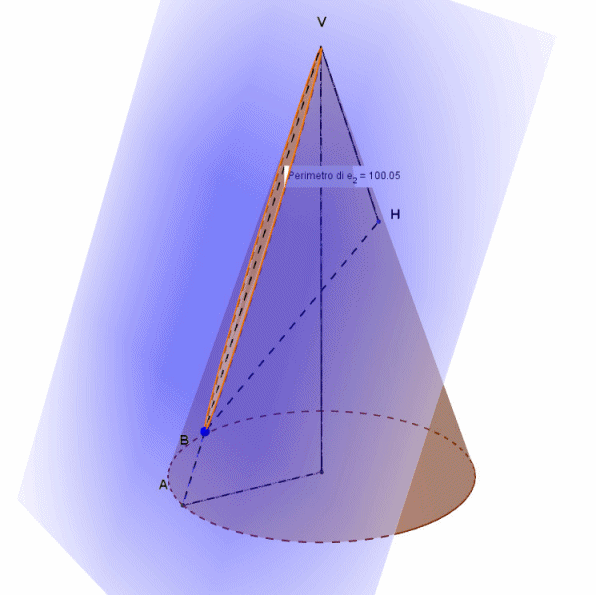
I valori numerici visibili nell'animazione sono quelli assunti dal perimetro dell'ellisse. Non compare l'unità di misura (metri, centimetri, millimetri...) perché è un ragionamento del tutto generale. Le effettive misure dipenderanno da quelle del modello geometrico preso in considerazione. Il piano che, intersecandosi con il cono, genera le suddette ellissi (colorato di azzurro nell'animazione) passa per il punto B ed è parallelo all'asse y, non indicato nell'animazione. In sostanza, nell'animazione l'origine degli assi coincide con il centro del cerchio di base del cono, l'asse x è disposto come il raggio del cerchio di base, l'asse z come l'altezza del cono e l'asse y passa ovviamente per il centro del cerchio di base ed è perpendicolare ai primi due assi. Il piano secante che genera le ellissi ruota attorno alla retta passante per B e perpendicolare al piano xz, anche essa non indicata nell'animazione. Tale retta è dunque parallela all'asse y. Pertanto , il piano secante, per qualsiasi valore dell'angolo di inclinazione, si mantiene parallelo all'asse y.

Cosa succede sviluppando nel piano le suddette ellissi ? La seguente figura riporta appunto lo sviluppo in piano di alcune di tali ellissi, tra cui quella già vista prima , ossia passante per B ed H:

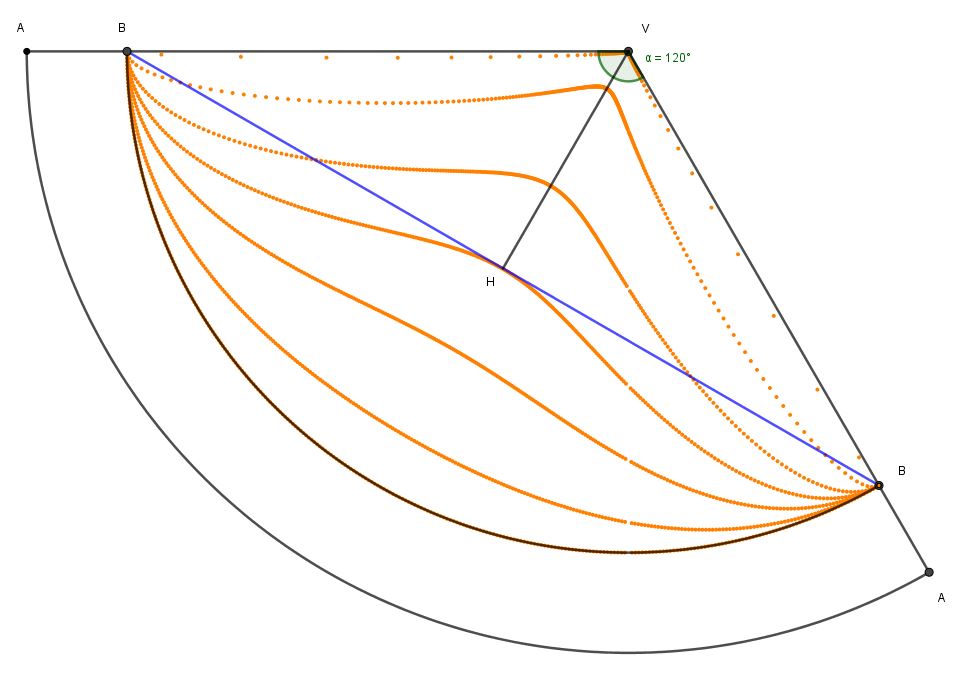
In particolare, quando il piano secante che genera l'ellisse è parallelo al piano xy, l'ellisse diventa una circonferenza e la sua curva equivalente nella vista piana è l'arco di circonferenza BB. Man mano che l'angolo di inclinazione del piano secante aumenta, tale curva si trasforma come si vede nella suddetta figura. Di queste ellissi non sappiamo ancora quale sia quella di minima lunghezza.

Ci chiediamo, quindi,  se, tra queste ellissi, quella passante per B ed H è quella che la lunghezza minore.  Prima di tutto, come si calcola il perimetro di una ellisse ? Purtroppo non esiste una formula esatta. In genere si fa uso di quella approssimata :

                         (1)

dove con p indichiamo qui il perimetro dell'ellisse, con a e b i due semiassi, maggiore e minore rispettivamente.

Tale formula fornisce risultati leggermente approssimati per eccesso.

Un'altra formula, più precisa, è quella che deriva dal calcolo integrale:

             (2)

dove con e indichiamo l'eccentricità dell'ellisse, definita dalla relazione:

Sfortunatamente, l'integrale visibile nella formula è un integrale ellittico completo di seconda specie, la cui soluzione esatta non esiste. Cioè, anche in questo caso, la formula porta a un risultato inevitabilmente approssimato.

Proviamo, comunque, a fare un po' di conti. Facciamo riferimento alla seguente figura, realizzata da Arturo con geogebra:

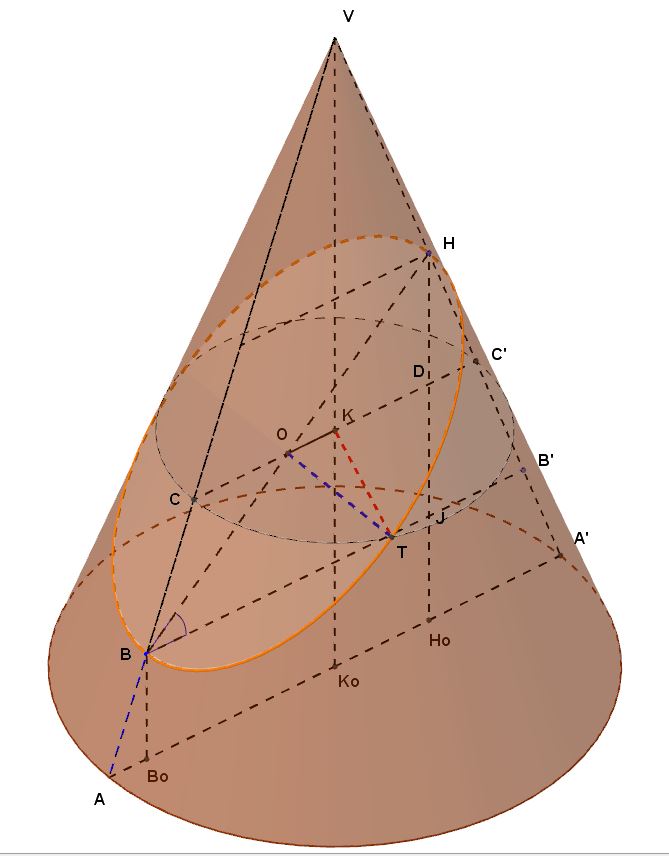
Vediamo quali sono i dati di partenza.

AB = l  (distanza tra i due punti misurata lungo la generatrice)

AKo = R (raggio di base del cono)

VK0 = H (altezza del cono)

AV= a (apotema del cono)

B'BH =  (angolo di inclinazione del piano secante a cui appartiene la generica ellisse passante per B, è la nostra variabile)

Siano (xB, 0, zb) e (xH, 0, zH) le coordinate, rispettivamente, del punto B (dato di partenza)  e del punto H (la cui posizione dipende dall'angolo di inclinazione .

Da semplici considerazione sulla similitudine dei triangoli AVK0 e BGK0  e dei triangoli ABBo e AVK0, si ottiene:

Per trovare le espressioni delle coordinate del punto H in funzione dell'angolo , lo considero come intersezione tra la generatrice del cono passante per H e per A' e la retta passante per B e inclinata di  rispetto al piano xy. La prima ha equazione cartesiana, nel piano xz (retta passante per il punto V e per il punto A'):

                   (3)

La seconda, invece, ha equazione (retta passate per il punto B e con coefficiente angolare uguale a tan  ):

     (4)

Mettendo a sistema la   (1) e la (2) ottengo le espressioni delle coordinate del punto H, in funzione dell'angolo :

L'asse maggiore dell'ellisse, come si vede dalla figura, è il segmento BH. Considerando il triangolo rettangolo BHJ, risulta:

BJ = BH cos                           (5)

Inoltre

BJ = BoKo + KoHo

Essendo K0 coincidente con l'origine degli assi, BoKo altro non è che, in  valore assoluto, l'ascissa del punto B,  , e K0Ho è, in valore assoluto, l'ascissa del punto H, , quindi:

BJ = +                       (6)

Dalla (5) e dalla (6), quindi, ricavo:

         (lunghezza dell'asse maggiore dell'ellisse passante per B e inclinata di  rispetto al piano xy)

Il semiasse maggiore sarà, ovviamente BH/2.

Vediamo ora di determinare l'espressione dell'asse minore dell'ellisse. Consideriamo, sempre con riferimento alla precedente figura, i due triangoli simili CVC' e AVA'. Poichè simili, vale la relazione:

cioè:

          (raggio del cerchio parallelo al piano xy e che passa per il centro O dell'ellisse)

Inoltre:

HC' lo ricaviamo considerando i triangoli simili VKoA' e HDC':

quindi:

A questo punto, considerando il triangolo rettangolo OKT, possiamo determinare con il teorema di Pitagora:

      (lunghezza del semiasse minore dell'ellisse passante per B e inclinata di  rispetto al piano xy)

Una volta note le espressioni del semiasse maggiore e di quello minore della generica ellisse in funzione dell'angolo , possiamo determinare l'espressione del perimetro dell'ellisse adottando la formula approssimata (1) e quella con l'integrale ellittico (2). La seguente figura mostra il grafico di tali due funzioni:

 

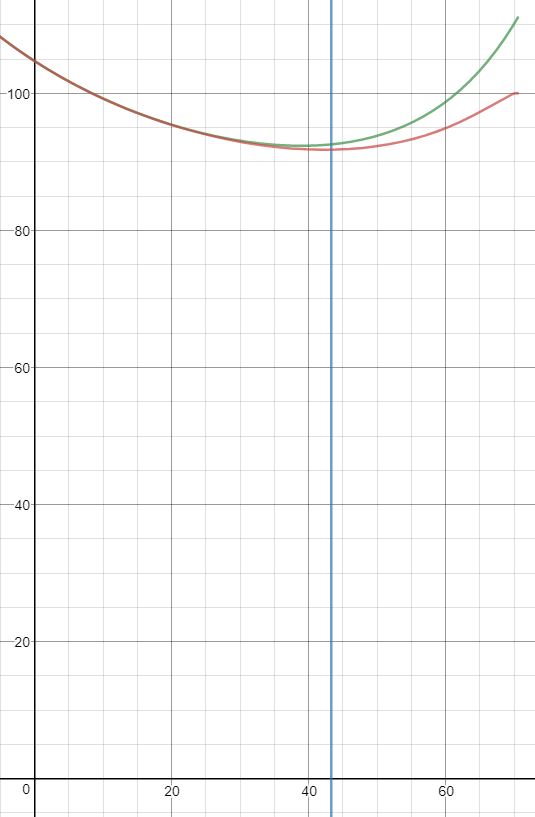
Sull'asse x riportiamo il valore dell'angolo  di inclinazione del piano secante e genera l'ellisse e sull'asse y riportiamo il valore del perimetro di tale ellisse. La curva verde è il grafico della funzione p() considerando la formula approssimata (1), mentre la curva rossa è il grafico della funzione p() considerando la formula con l'integrale ellittico. La retta verticale blu ha equazione x=43,3 ( gradi)  e ci serve per determinare i valori di  p() quando, appunto,  = 43,3. Tale valore dell'angolo è quello corrispondente alla geodetica del problema (segmento BH nella figura n.9). Dalla suddetta figura si direbbe che la curva verde ha il punto di minimo per valore dell'angolo  diverso da 43,3 , mentre la curva rossa sembra avere il punto di minimo in corrispondenza di tale valore dell'angolo. Facendo, tuttavia, uno zoom sul grafico, otteniamo questa figura:

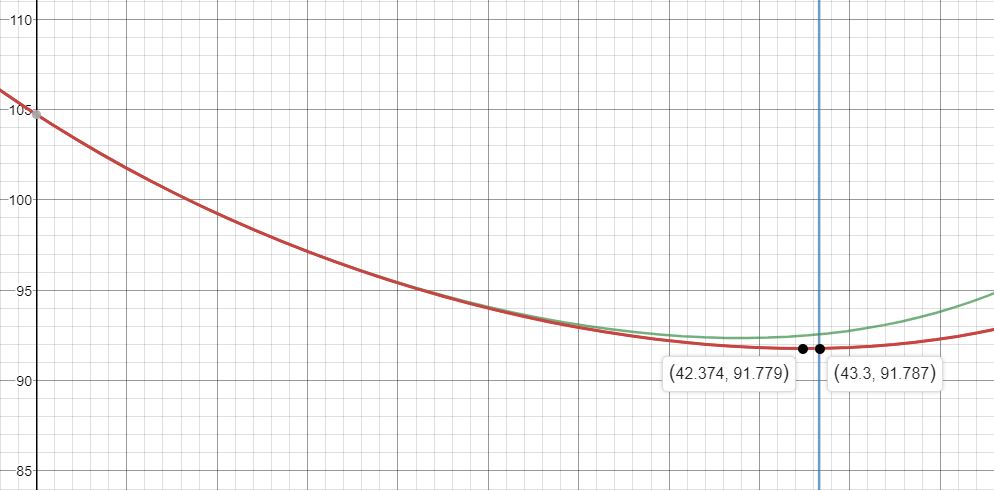
In questa abbiamo evidenziato il punto di minimo della curva rossa (il punto nero a sinistra) e il punto di intersezione con la retta x=43,3 (il punto nero a destra). Si vede, pertanto, che anche con la curva rossa, cioè anche considerando la formula con l'integrale ellittico, la minima lunghezza dell'ellisse non si ha per il valore dell'angolo corrispondente alla geodetica.

C'è tuttavia da ricordare che anche la formula con l'integrale ellittico è approssimata, poiché, come si è detto, non esiste una soluzione esatta dell'integrale ellittico in questione. E solo disponendo di una formula  del calcolo "esatto" del perimetro dell'ellisse, saremmo in grado di dire se l'ellisse di minimo percorso contiene o meno il punto H e, quindi, di affermare che  le lievi differenze riscontrate con le formule che abbiamo utilizzato  sono solo frutto della approssimazione del calcolo.

A questo proposito, Fabrizio ha infine provato a vedere cosa succede variando i parametri geometrici del cono. Sinora, infatti,si è considerato il cono del quiz, con un dato raggio e una data apotema e si è visto che , per questo cono, l'ellisse di minima lunghezza sembrerebbe passare, al limite, per il punto H della geodetica. Ma è così in generale, ossia anche per coni di differenti parametri geometrici ? A seguito delle prove fatte da Fabrizio la risposta è no. Vi sono, cioè, coni per i quali , fissato il punto B e considerate la geodetica e l'ellisse di minima lunghezza passanti per tale punto, si verifica che l'ellisse non passa e di parecchio per il punto H (il punto di massima quota della geodetica). A quel punto non è più questione di approssimazione della formula per il calcolo del perimetro.

Ci pare, in definitiva, di poter concludere che, in generale, l'ellisse di minima lunghezza passante per un punto B di un cono non passa dal punto H della geodetica.

 

EPILOGO

Dal nostro "parlare e pensare su ciò che è successo" possiamo trarre alcune utili conclusioni.

E' bene ricordare che la linearità può essere ingannevole, non trasferibile in territori diversi (il segmento sullo sviluppo non si collega ad un piano nello spazio).

Meglio dubitare anche delle cose che "appaiono" sicure,  una verifica preliminare, apparentemente superflua, ci può evitare di  avventurarci su un percorso sbagliato. Meglio, addirittura, risolvere il problema in più modi indipendenti per verificare il risultato ottenuto, come, per fortuna, è successo nel nostro quiz. Potremmo avere delle sorprese e imparare qualcosa di nuovo.

Se possibile, rendere tangibili gli oggetti su cui ragioniamo, osservandoli potremmo scoprire cose del tutto inattese.

Se ci pensate un attimo, queste affermazioni possono essere estese a contesti ben più ampi di quello geometrico, possono essere interpretate come metafore applicabili alla vita quotidiana.

 

QUI troverete altri percorsi da calcolare!

QUI l'Infinito Teatro dei Quiz presenti nel Blog