Diamo le risposte alle varie domande della seconda parte del quiz sul monte cono di Papalla, trascurando la parte relativa all'ellisse, sulla quale c'è chi sta lavorando duro e pubblicherà a breve una dettagliata trattazione (eccola QUI). Questa parte segue pari pari quanto riportato nei commenti da Fabrizio, con pochissime variazioni.

La riposta alla domanda 1c) merita una trattazione a parte, dato che se è vero che esiste un'ellisse di minima lunghezza, essa non è, però, una geodetica, come io avevo frettolosamente suggerito. Maurizio, Fabrizio e, soprattutto, Arturo se ne sono accorti e hanno trovato pane per i loro denti... Ne vedremo delle belle. Fabrizio ed io ci siamo invece dedicati alle risposte più semplici.

1a)

Riprendiamo in mano il settore circolare equivalente alla superficie conica aperta su un piano, come già fatto la volta scorsa (QUI), in Fig. 1.

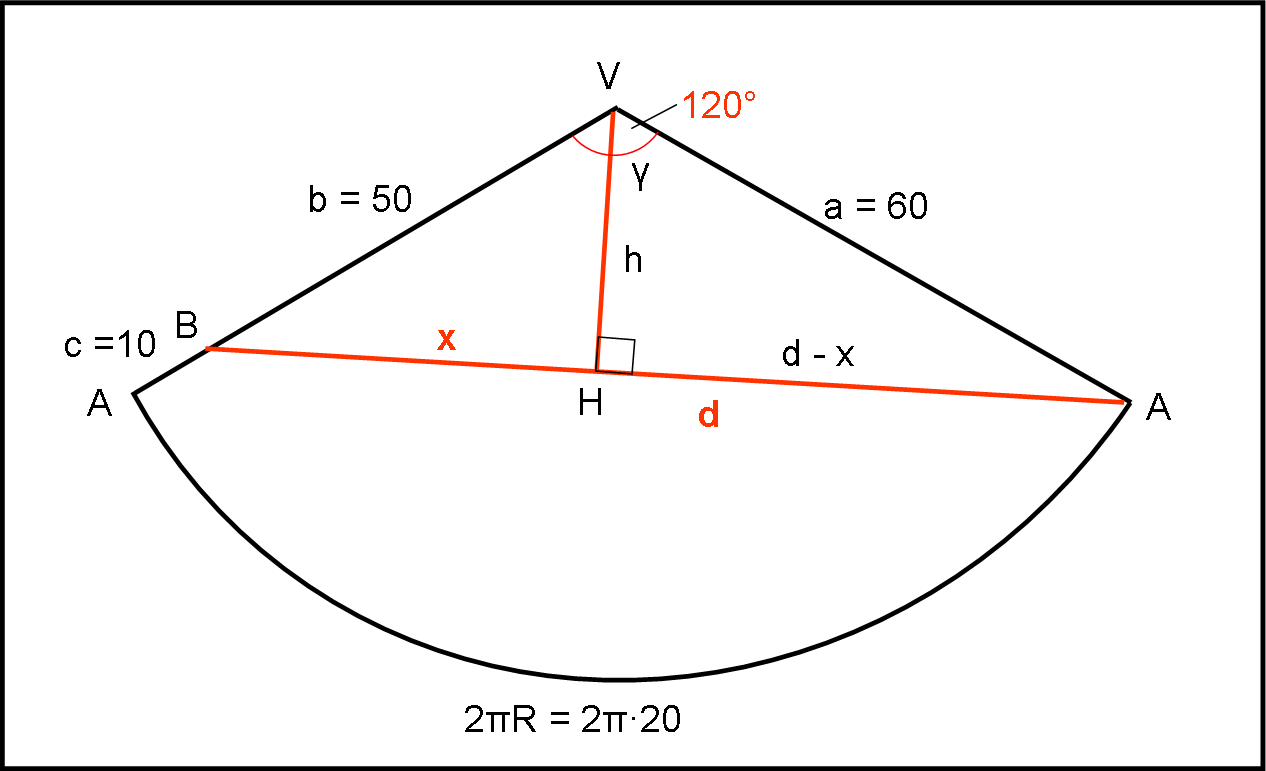
Il percorso di minima distanza tra quelli che fanno un giro del cono  è senza dubbio il segmento congiungente A con B (rosso) che, come già visto, ha distanza variabile rispetto al vertice del cono V. C'è anche un altro percorso della stessa lunghezza che fa un giro completo. E' quello simmetrico che gira in senso orario.

Sia a l’apotema, cioè VA, che nel caso pratico vale:

VA = a = 60

Dato che AB = c = 10 (lungo la generatrice) abbiamo che:

VB = b = a – c = 50

Il raggio di base del cono è:

R = 20

Chiamiamo γ l’angolo al vertice del cono aperto e cerchiamo di ricavarlo.

Sappiamo che l’arco di cerchio del cono aperto è uguale a 2πR , ma questo arco è anche uguale a quello del cerchio di raggio a, che è relativo proprio a un angolo al vertice uguale a γ. Possiamo quindi scrivere la relazione:

2πR = γa

Da cui:

γ = 2πR/a = 360·20/60 = 120°

Per ricavare velocemente la lunghezza d del segmento AB, nel cono aperto, basta riferirsi al triangolo ABV, di cui conosciamo l’angolo in V e due lati (a e b), e applicare il teorema di Carnot:

d² = b² + a² - 2ab cos(γ)

d² = 50² + 60² – 2·50·60 cos(120)

AB² = 9100

AB = 10√91 = 95.4

1b)

Il punto più vicino al vertice del cono aperto del segmento AB è H, dove VH è la perpendicolare h al segmento AB. Superato il punto H, la distanza dalla vetta inizia a crescere. Quindi il tratto HB è in discesa e la lunghezza del tratto HB  è proprio la lunghezza del tratto in discesa richiesto.

Per ricavare la lunghezza HB, che indichiamo con x, utilizziamo le espressioni di h ottenute sia attraverso il triangolo rettangolo BHV sia attraverso il triangolo rettangolo AHV.

h² = b² – x²

h² = a² – (d – x)²

Uguagliando le due espressioni si ha:

b² – x² = a² – (d – x)²

b² – x² = a² – d² – x² + 2dx

2ax = b² – a² + d²

x = (b² – a² + d²)/2d

x = (50² - 60² + 9100)/(20 · √91)

x = 400/√91 = 41.9   (tutti da percorrere sul ghiaccio…)

2)

Dato un cono, generico, sono noti γ, R e a (Fig. 2)

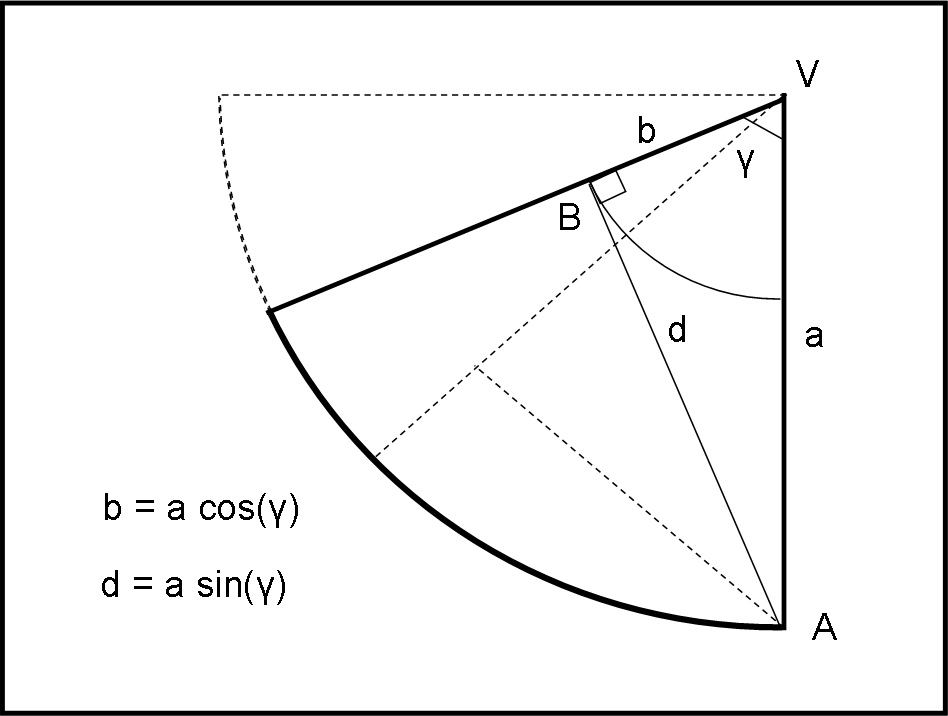
Affinchè il tratto AB sia sempre in salita (e quindi non tocchi il ghiaccio) occorre che il punto H di figura 1, cioè il punto di minima distanza da V, non sia all'interno del tratto AB. La situazione limite l'abbiamo quando H coincide con l'estremo B. In altre parole quando VBA è un angolo retto.

La relazione che interessa si deriva facilmente dal triangolo VBA, che nel caso limite è rettangolo, ed è:

cos(γ) = b/a     (il rapporto tra cateto adiacente all'angolo ed ipotenusa è per definizione il coseno dell'angolo)

Se cos(γ) > b/a, allora il punto H è all'esterno del segmento AB ed il percorso non passa per la zona ghiacciata.

Se cos(γ) < b/a, allora il punto H è all'interno del segmento AB ed il percorso passa per la zona ghiacciata.

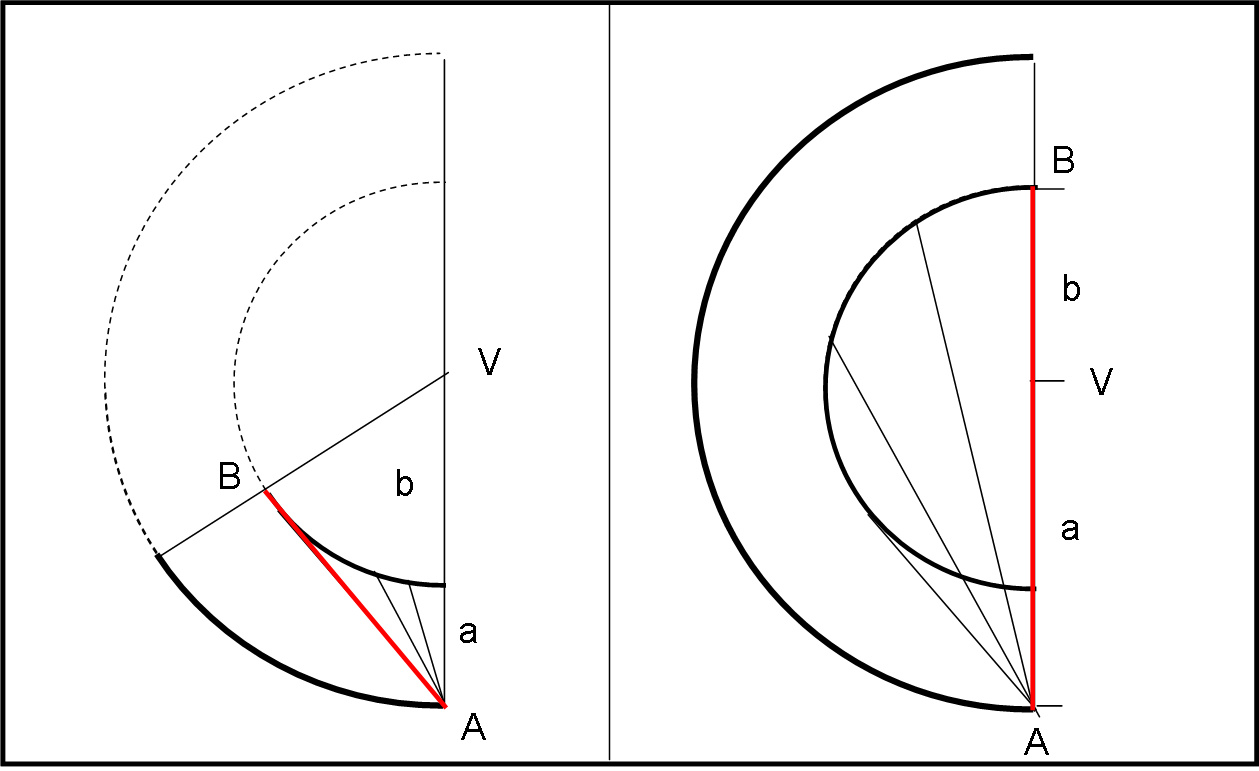
Nella FIg. 3 sottostante sono evidenziate le tre situazioni.

Fino a un certo valore di γ (cos(γ)>b/a, parte sinistra della figura) il percorso tra A e B avviene solo in salita senza toccare il ghiaccio.

Per un particolare valore di γ (cos(γ)=b/a) il percorso tra A e B è tangente alla zona ghiacciata proprio nel punto B. Il fatto che sia tangente conferma che i segmenti AB e VB sono ortogonali.

Dopo (cos(γ)<b/a, parte destra della figura) si inizia ad attraversare il ghiaccio ed il percorso tra A e B ha una parte in salita e una in discesa.

3)

Quando γ cresce fino a 180° il percorso AB passa per il vertice V.

In questo caso possiamo prendere a e b qualsiasi, ma il risultato non cambia.

Per quanto abbiamo visto precedentemente (teorema di Carnot) la distanza d diventa esattamente d = a + b per γ = 180°. Dopo di che AB non appartiene più al cono. Infatti, per andare da A a B lungo una geodetica che faccia un giro del cono non si può superare un angolo γ = 180°.

Ricordando che

γ = 2πR/a

abbiamo, per γ = π :

R/a = 1/2

Da cui

φ = 30°

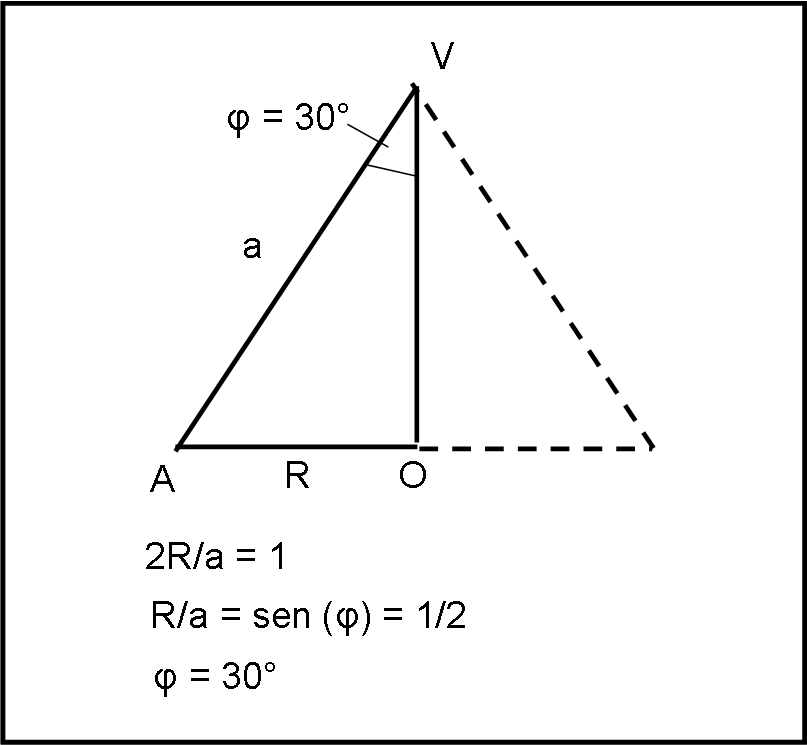
L'angolo tra apotema e altezza del cono non può superare 30° affinchè possano esistere delle geodetiche tra A e B (Fig. 4) che aggirino il cono.

Risolti questi quesiti piuttosto semplici, tenetevi forte e siate pronti a scontravi con ellissi e quasi-ellissi...

 

QUI troverete altri percorsi da calcolare!