Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"

Anche se si discosta dal nostro caro numero, vale la pena dedicare questo articolo al terzo grande problema insolubile con riga e compasso: la duplicazione del cubo. Vi è una leggenda che spiega come questo problema sia nato da un’esigenza più che concreta.

 

La pestilenza di Delo

La piccola isola di Delo venne colpita da una terribile pestilenza e la popolazione disperata si rivolse all’oracolo di Apollo per cercare di capire cosa poteva essere fatto. Egli rispose che il dio pretendeva un tempio cubico che fosse grande il doppio di quello attuale. Gli isolani partirono subito in quarta, raddoppiando semplicemente il lato del cubo. Niente cambiò e fu presto chiaro che agendo in questo modo il cubo finale sarebbe stato otto volte più grande (come volume) e non solo il doppio. Il problema dimostrò subito di essere irrisolvibile con riga e compasso e molti si dedicarono a metodi non “classici”, con costruzioni più complicate. Alcune veramente geniali, altre estremamente complesse anche utilizzando l’algebra e la geometria analitica. Noi ne ricorderemo qualcuna, sia per la loro eleganza sia per l’introduzione di nuove curve.

Bastano due triangoli...

Pur con le incertezze del caso, il problema fu genialmente trasformato da Ippocrate di Chio (l’uomo delle lunule) in un problema a due dimensioni. Il tutto si basa su rapporti tra cateti e altezze di triangoli rettangoli simili, anticipando decisamente il secondo teorema di Euclide. Questo fatto, malgrado le incertezze su “chi ha fatto cosa”, farebbe capire come Euclide abbia utilizzato materiale e idee molto più antiche per scrivere il suo fondamentale trattato.

Vediamo come Ippocrate ha trasformato un problema tridimensionale in uno bidimensionale.

Consideriamo la Fig. 21, dove vengono evidenziati alcuni segmenti relativi ai due triangoli costruiti in modo "intrecciato".

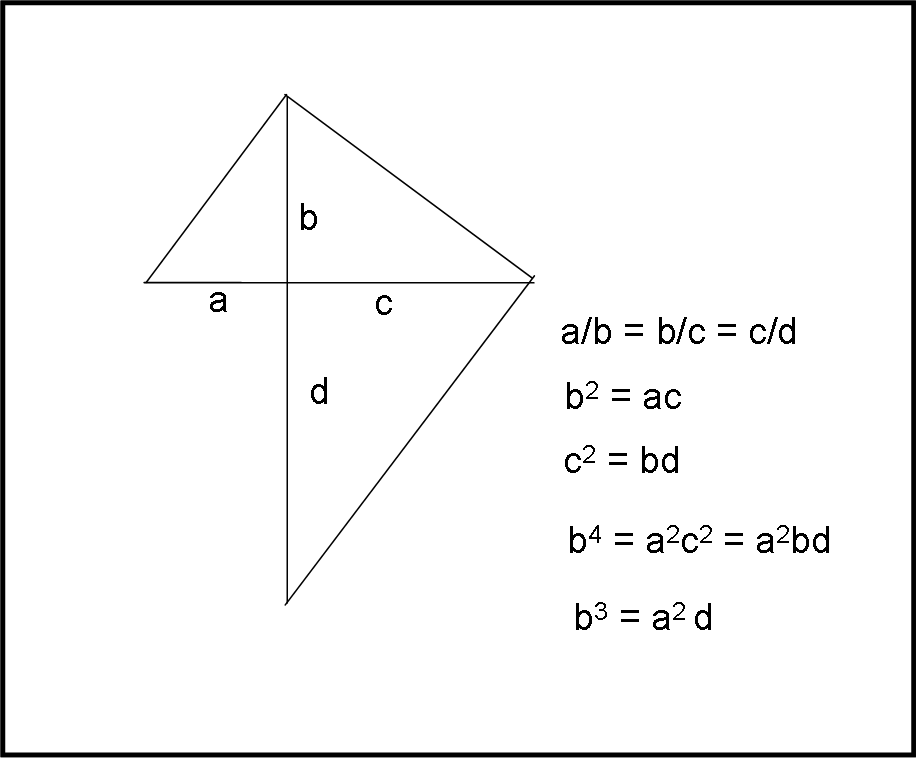
Scrivendo le proporzioni tra triangoli simili (in altre parole, utilizzando due volte il secondo teorema di Euclide) si ottiene:

a/b = b/c = c/d

ossia:

b² = ac

c² = bd

Quadriamo la prima e sostituiamo c² ottenuto dalla seconda

b⁴ = a²c² = a²bd

b³ = a²d

A questo punto possiamo decidere di costruire il segmento d in modo che risulti uguale a ma. Si otterrebbe:

b³ = m a³

Se m fosse proprio uguale a 2, avremmo la fondamentale relazione

b³ = 2 a³

che, espressa a parole, dice che il volume di un cubo di lato b è il doppio del volume di un cubo di lato a. b sarebbe proprio il lato cercato…

b = (2)^1/3 a

La presenza della radice cubica di 2 chiarisce subito perché riga e compasso sarebbero insufficienti. Riassumiamo graficamente in Fig. 22 (in 3d) quello che abbiamo fatto, per meglio comprendere la semplicità della costruzione.

Costruiamo un cubo di lato b e un parallelepipedo a base quadrata di lato a e altezza d. Possiamo variare d mettendolo in relazione ad a (tre volte a, due volte a, otto volte a…). Se scegliamo proprio che d sia due volte a, otteniamo un parallelepipedo formato da due cubi di lato a che è equivalente (come volume) al cubo di lato b. In altre parole, il volume del cubo di lato b è uguale a DUE VOLTE il volume del cubo di lato a.

La costruzione del lato b in funzione del lato a può essere ottenuto attraverso uno strumento mostrato in Fig. 23.

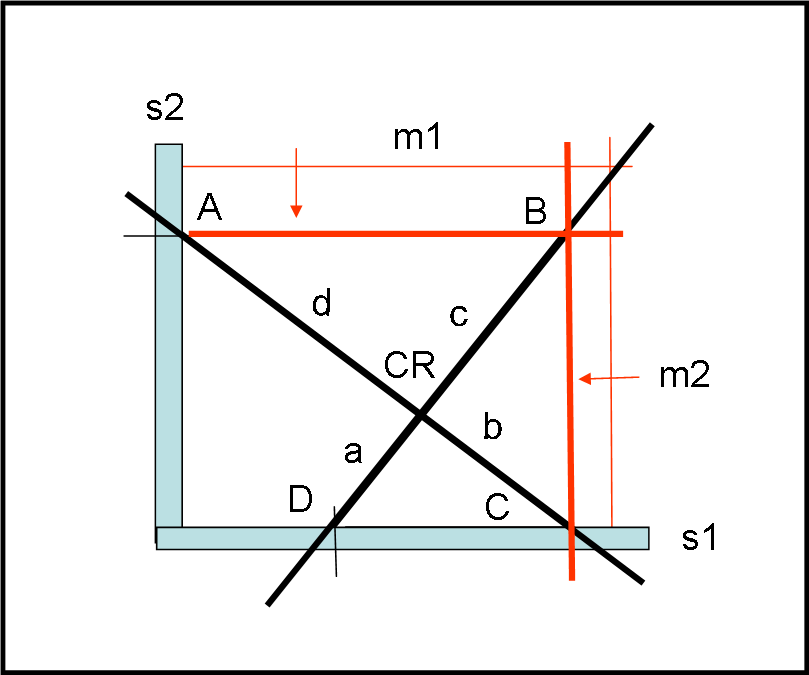
Si costruisce una croce di due aste perpendicolari (CR) e si sistema su due aste rigide s1 e s2 anch’esse perpendicolari tra loro, in modo da ottenere d = 2a. A questo punto, attraverso due aste m1 e m2 scorrevoli su s1 e s2 si ottiene la figura ABCD, che riprende pari pari la Fig. 1. Infatti si ottiene immediatamente che:

b³ = 2a³

b è proprio il lato richiesto da Apollo per far terminare la terribile epidemia di Delo!

 

Cissoide di Diocle (II sec a.C.)

Diocle “inventa” una curva diventata celebre anche in tempi più recenti: la cissoide.

Vediamo di costruirla. Consideriamo una circonferenza di diametro OA (Fig. 24). Tracciamo una perpendicolare al diametro OA da un punto qualsiasi N che incontri la circonferenza in M (e in R).

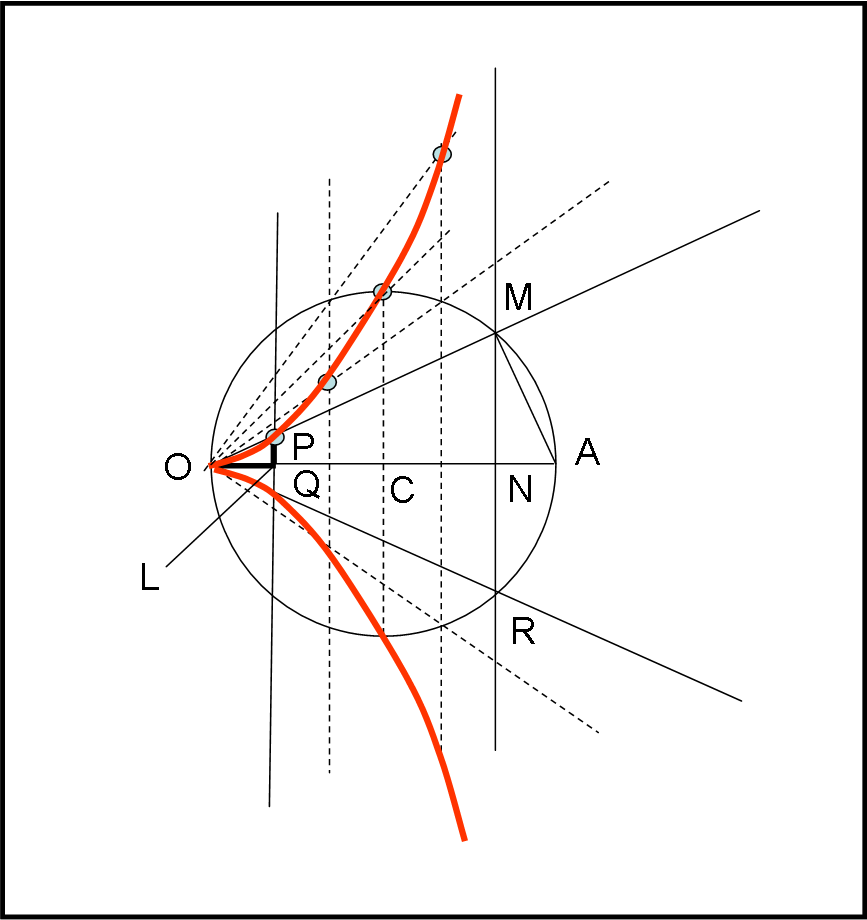
Congiungiamo O con M (e con R). Segniamo il punto L sul diametro in modo che OL = NA e tracciamo una perpendicolare a OA, che individua i punti P e Q sulle rette per M e R.

Il luogo dei punti P e Q così costruiti, al variare del punto M, è proprio la nostra cissoide.

Dal triangolo rettangolo OMA si ha:

ON/MN=MN/NA

Dai triangoli rettangoli simili PLO e MNO abbiamo:

ON/MN = OL/LP

Ma OL = NA per costruzione, da cui:

ON/MN = MN/NA = NA/LP

Otteniamo, analogamente al caso precedente, che MN e NA sono due medi proporzionali tra ON e PL.

Vediamo come si arriva al lato del cubo duplicato, calcolando, inizialmente, l’equazione della curva (Fig. 25).

Poniamo l’origine degli assi x e y in O. Chiamiamo a il diametro del cerchio. Abbiamo, perciò:

x = OL = NA

y = LP

Sappiamo, da quanto visto precedentemente, che:

x/y = NA/LP = ON/NM

NM = √(ON · NA)

ON = AL = a – x

x/y = (a-x)/√(x(a-x))

y = x √(x(a-x))/(a-x)

y = x √(x(a-x))/√((a-x)(a-x))

y = x √(x(a-x)/(a-x)(a-x))

y = x √(x/(a-x))

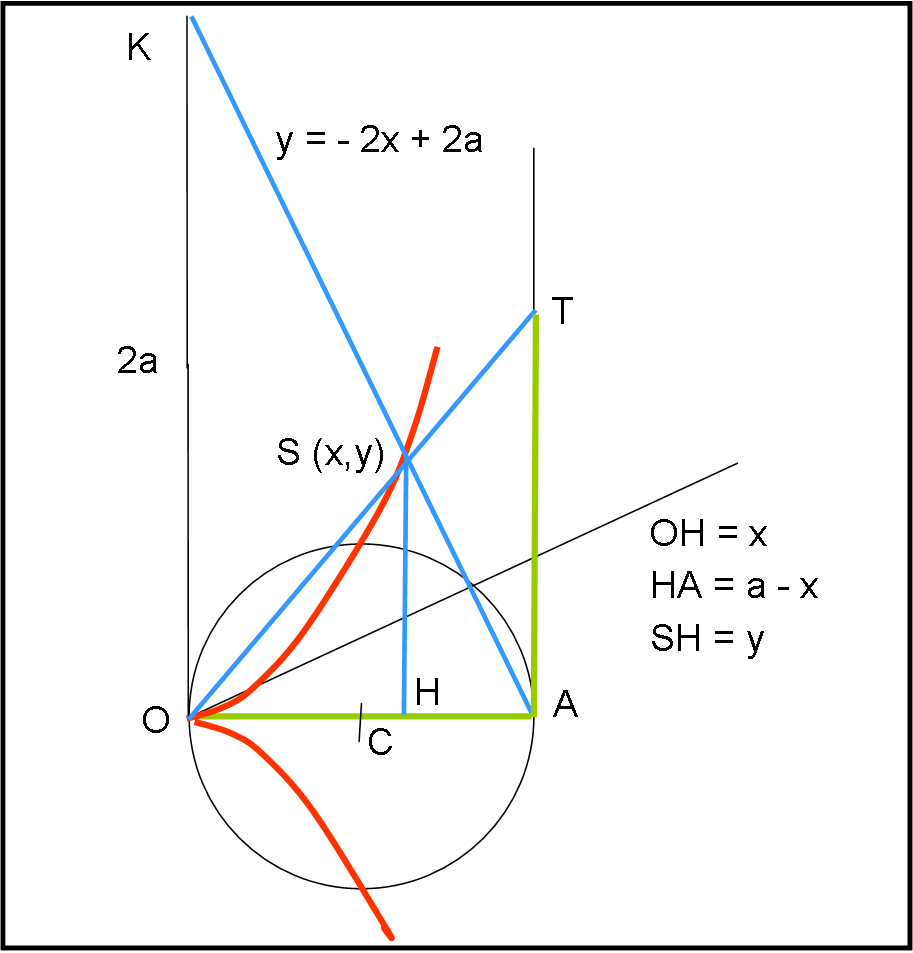
Consideriamo il punto K sull’asse delle y tale che OT = 2a e scriviamo l’equazione della retta passante per K e per A:

y = - 2x + 2a

Intersechiamo la cissoide con la retta per K (punto S). Si ottiene il sistema:

y = x √(x/(a-x))

y = - 2x + 2a

Dalla seconda:

y = 2(a-x)

che sostituita nella prima, porta a scrivere:

2(a-x) = x√(x/(a-x))

2 = √(x³/(a-x)³)

Un modo molto interessante per scrivere il numero 2 ! Ma, andiamo avanti…

Tracciamo la retta da O a S fino a intersecare in T la retta da A perpendicolare a OA.

Consideriamo i triangoli simili OAT e OHS. Possiamo scrivere:

AT/HS = a/x

AT =  a · HS/x

Facciamo il cubo di entrambi i membri:

AT³ = (a HS/x)³

HS è pero y, che abbiamo visto prima valere:

y = x²√(x/(a-x))

Sostituendo, si ottiene:

AT³ = (a x√(x/(a-x))·1/x)³ = a³ (√(x/(a-x)))³ = a³ √(x³/(a-x)³)

(Ricordando che (m^1/2)³ = m^3/2 = (m³)^1/2)

Ma… l’ultima radice quadrata è proprio ciò che abbiamo visto poco fa essere uguale al numero 2, e, di conseguenza:

AT³ = 2 a³

Il cubo di lato AT è due volte il cubo di lato uguale al diametro del cerchio di partenza.

Ovviamente, noi abbiamo usato la geometria analitica, ma Diocle utilizzò un sistema “meccanico”… prodigioso!

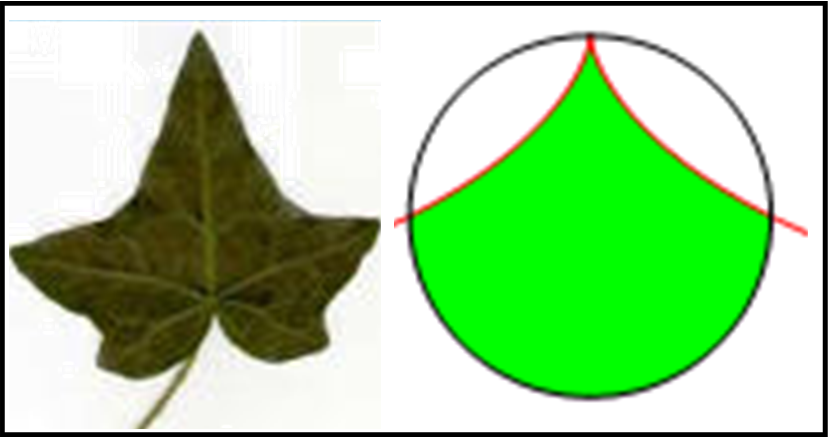
Perché è stata chiamata cissoide? L’area compressa tra la curva e la circonferenza di partenza ricorda proprio la foglia dell’edera (Fig. 26). Un po’ di fantasia non fa mai male... (la parola "cissoide" proviene dal greco kissoeidēs, "a forma di edera", composto di kissos, edera, e oeidēs, forma).

 

Concoide di Nicomede (III – II sec. a.C.)

La concoide di Nicomede può risolvere sia il problema della trisezione di un angolo, sia quello della duplicazione del cubo.  Vediamo di costruirla: è molto bella e divenne celebre nel XVII sec., quando la studiarono a fondo sia Huygens che Fermat. Newton, addirittura, propose di inserirla, insieme al cerchio e alla retta, tra le curve che tutti i “geometri”, dovrebbero conoscere.

Consideriamo, in Fig. 27, un punto O, una retta r, la loro distanza a, e un segmento AB = k.

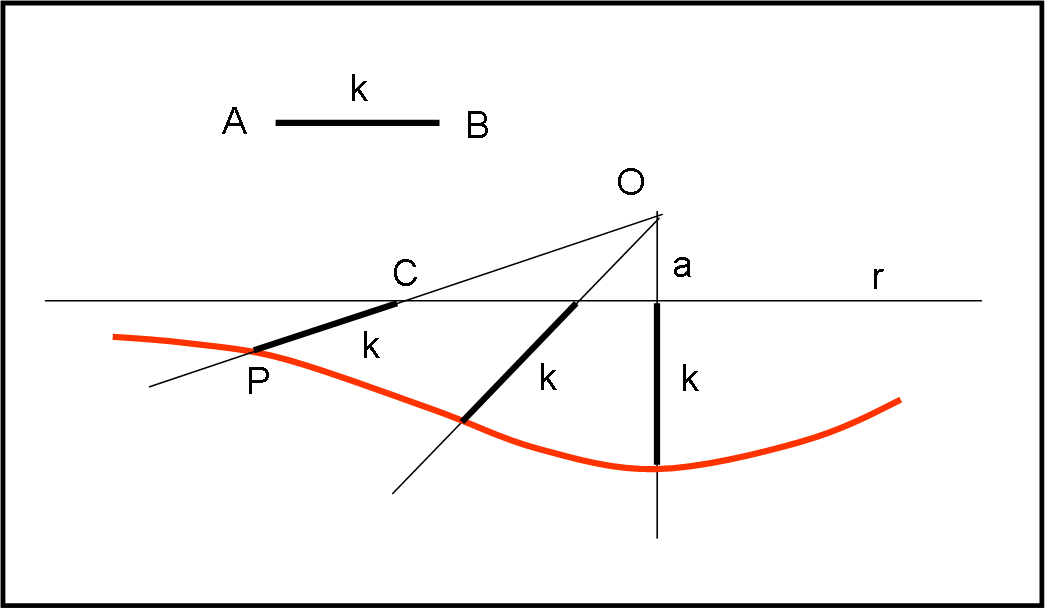
Tracciamo da O una retta s qualsiasi. Su questa retta, a partire dal punto d’incontro C con r, si riporta il segmento di lunghezza k. Il luogo descritto dai punti P, al variare di s, prende il nome di concoide.

In realtà, nella Fig. 27 vediamo solo una parte della curva, quella sotto la retta r, che era servita a Nicomede. La seconda parte è più fantasiosa ed è quella percorsa dal punto P’ al di sopra della retta r (basta considerare la circonferenza di centro C su r e raggio k). Questa parte dipende in modo spettacolare da k e dalla distanza a di O rispetto alla retta r (Fig. 28).

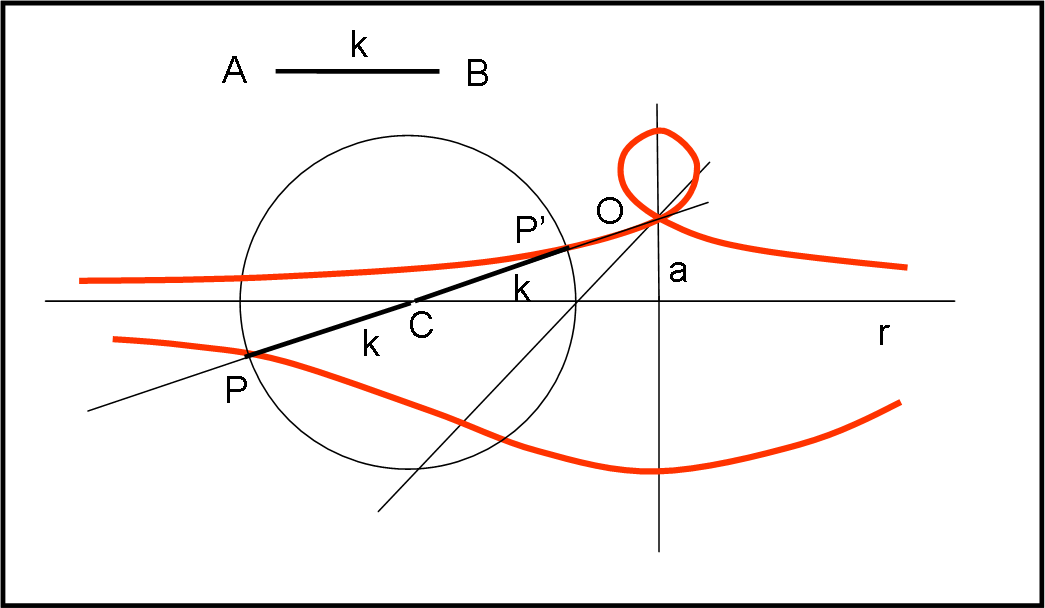
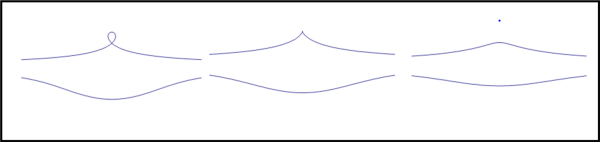
Se k > a otteniamo un nodo nel punto O, se k = a, si ottiene una cuspide e se k < a un punto isolato, che è  al di fuori della curva, ma le appartiene… In Fig. 29 vediamo i tre casi.

Provate per credere, la costruzione è semplice… così come determinare la sua equazione (la concoide è una quadrica). Possiamo anche aggiungere che la concoide è una cissoide di una circonferenza con il punto O posto al suo centro. Evitiamo i calcoli, ma con un po’ di fatica si arriva alla solita doppia proporzionalità che porta alla soluzione della duplicazione del cubo.

Concoide prende il nome da conchiglia, come si vede bene nella Fig. 30.

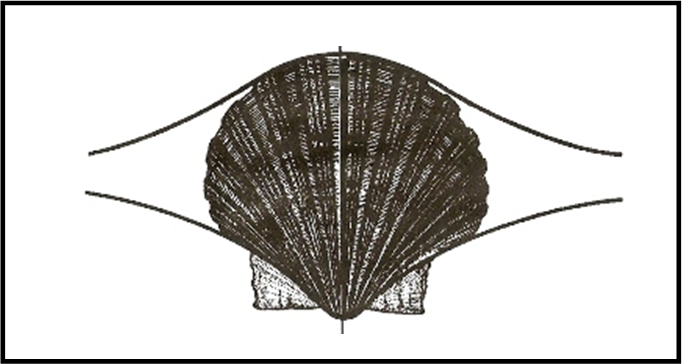
Evitiamo anche la più complessa determinazione effettuata da Archita (430 – 360 a.C.), direttamente nelle tre dimensioni. Una trattazione veramente geniale se si pensa che venne ottenuta senza l’uso di coordinate cartesiane.

Concludiamo, invece, con un metodo estremamente più semplice e immediato, utilizzato da Menecmo nel IV sec. a. C. attraverso l’intersezioni di due parabole  e/o di una parabola e un’iperbole. L’approccio è molto importante perché segna l’inizio delle sezioni coniche e, a quanto risulta, è proprio Menecmo, maestro di Alessando Magno, a descriverle per primo.

 

Soluzioni di Menecmo

La base di partenza è quella di Ippocrate di Chio e utilizza la ormai ben nota doppia proporzione:

a/x = x/y = y/2a

che porta alla espressione fondamentale:

x³ = 2a³

Sono convinto che molti di voi saprebbero trovare velocemente le equazioni delle due parabole… Provate… Fatto? Bene andiamo avanti e facciamoci aiutare dalla Fig. 31.

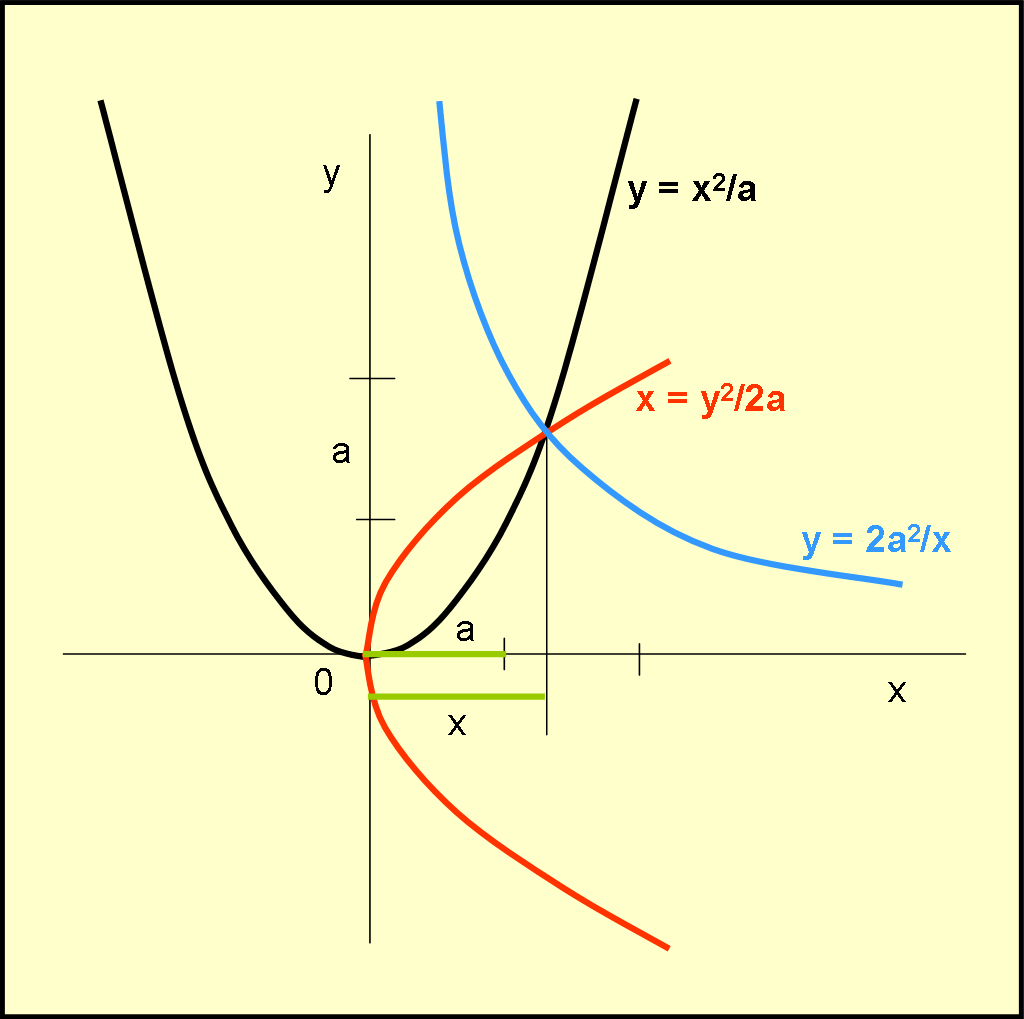
Dalla prima proporzione si ricava:

a/x = x/y

y = x²/a                   …. (1)

Dalla seconda:

y² = 2ax

x = y²/2a                 …. (2)

Facendo l’intersezione tra le due parabole (sostituendo la (1) nella (2)) si ha:

x = x⁴/(2(a²·a))

x³ = 2 a³

Che è proprio ciò che si cercava di ottenere. Veramente brillante!

Ma dalle proporzioni di prima si può anche scrivere:

a/x = y/2a

y = 2a²/x              …. (3)

che è un’iperbole, di cui si può considerare l’intersezione con la parabola (1)

Ossia tra

x = y²/2a

e

y = 2a²/x

Inserendo la seconda nella prima si ottiene subito:

x = 4a⁴/2ax²

e, ancora una volta:

x³ = 2 a³

Ancora un piccolo sforzo…

 

Il mesolabio di Eratostene (276 -194 a.C.)

Prima di lasciare (insoluto “classicamente”) il problema di Delo, vale la pena ricordare Eratostene (sì, proprio colui che attraverso un asta rigida, un dromedario e una prodigiosa mente riuscì a calcolare il diametro terrestre, ne abbiamo parlato QUI), che, rifacendosi direttamente a Ippocrate di Chio, costruì uno strumento apposito per  inserire due medi proporzionali tra due segmenti dati a e b. Ovviamente, nel caso che uno sia doppio dell’altro si ritorna alla duplicazione del cubo. E’ interessante riportare ciò che egli scrive a Tolomeo III , aggiungendo un’altra leggenda a riguardo:

“Narrano che uno degli antichi poeti tragici facesse apparire sulla scena Mino (re di Creta) nell’atto di far costruire una tomba al figlio Glauco; e che Mino, accorgendosi che questa era lunga da ogni lato soltanto cento piedi, dicesse: ‘troppo piccolo spazio accordasti a un sepolcro di re; raddoppialo, conservandolo sempre di forma cubica, raddoppia subito tutti i lati del sepolcro’. Ora è chiaro che egli si ingannava. Infatti, duplicandone i lati, una figura piana si quadruplica, mentre una solida si ottuplica. Allora anche fra i geometri fu agitata la questione in qual modo si potesse duplicare una data figura solida qualunque, conservandone la specie. E questo problema fu chiamato duplicazione del cubo, o anche problema di Delo, perché in seguito anche i Delii, spinti dall’oracolo a duplicare un altare cubico, caddero nella medesima difficoltà”. Poi continua: “Ippocrate da Chio trovò per primo che se fra due linee rette delle quali la maggiore sia doppia della minore si inseriscono due medie in proporzione continua, il cubo sarà duplicato”.

Lo strumento era formato da tre tavolette di colore diverso che potevano scorrere una sull’altra e sulle quali si poteva misurare l’altezza su uno spigolo. Tracciando le diagonali delle tre tavolette e impostando sulla prima il valore di a e sull’ultima il valore di b, si faceva passare una corda tra a e b tenuta tesa da un peso. Facendo coincidere punti particolari delle tavolette si ottenevano meccanicamente i medi proporzionali.

Meglio di tante parole, in Fig. 32 vediamo lo schema delle tre tavolette prima (a sinistra) e dopo (a destra) lo scorrimento

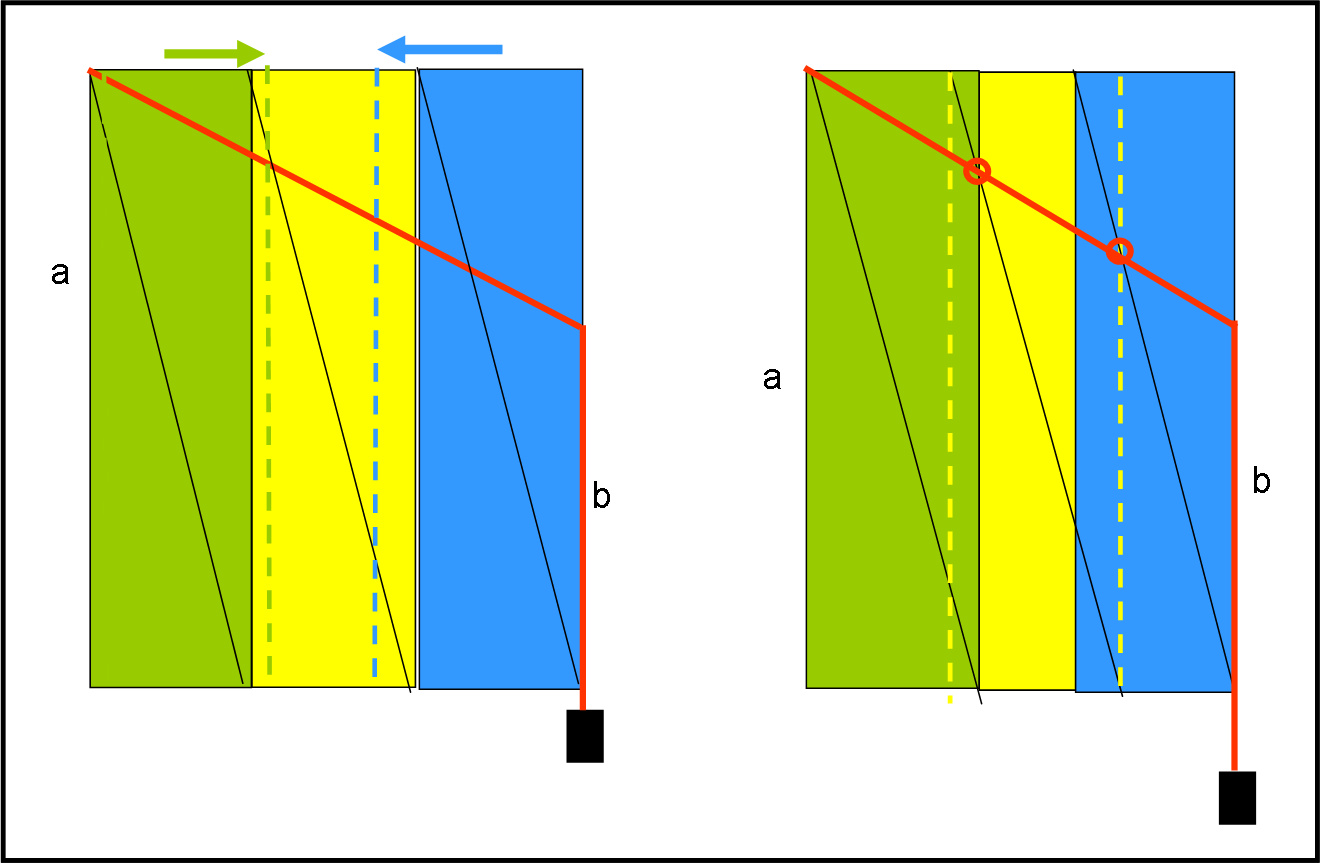
Geogebra ci mostra l’azione completa.

https://www.geogebra.org/m/NDnPtfVN

Bene, anche il problema di Delo ha avuto una sufficiente trattazione, malgrado resti insolubile con  i soli riga e compasso. Possiamo tornare al nostro pi greco...

 

QUI gli altri articoli dedicati all'infinita storia del pi greco