Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"

Non considerate noioso questo articolo. Da un lato abbiamo a che fare con problemi di geometria apparentemente più che banali, ma, dall'altra, entriamo prepotentemente nella Scuola di Atene, dove dire "geometria" è un modo di vivere e di pensare. Seguendo poche regole prefissate, siamo in grado di ottenere ciò che l'algebra e la geometria analitica ritroveranno dopo secoli. Un viaggio entusiasmante e -soprattutto- molto divertente.

Lasciamo, momentaneamente, da parte il nostro pi greco e facciamo un bel salto temporale, immaginando di entrare nell’Accademia, la Scuola di Platone. Probabilmente, leggeremmo sul frontone d’ingresso la frase: “Nessuno entri, che non sia geometria”.

Il succo è che anche la matematica e la geometria, in particolare, fanno parte del mondo filosofico e metafisico di Platone. Devono essere perfezione e armonia come tutta la visione del mondo. La geometria, in particolare, deve usare solo strumenti semplici e puri per riuscire a costruire qualcosa di sempre più complesso a partire da poche basi fondamentali. Un processo geometrico e non meccanico. Solo così le figure geometriche possono essere costruite perfettamente e rigorosamente all’interno di un dato sistema di regole.

Euclide permette di stabilire queste regole, che possono essere sintetizzate a partire dai suoi primi tre postulati, attraverso un gesto formale e intuitivo, per poi procedere nella costruzione di qualsiasi figura. Questo gesto si traduce nell’uso di solo due strumenti : una riga non graduata e un compasso “molle” (o -se preferiamo- … a “scatto”)

Spieghiamoci meglio: la riga non deve avere segni che permettano di stabilire delle distanze su di lei, ma serve solo per congiungere punti e allungare all’infinito i segmenti. Il compasso molle permette di tracciare cerchi prendendo un punto come origine e l’altro come raggio del cerchio, ma non può assolutamente servire per trasportare un segmento da una posizione a un altra. In altre parole, è come se il compasso permettesse di essere aperto fino al limite voluto, ma, una volta descritto il cerchio, tornasse automaticamente a chiudersi. Come già detto, queste definizioni nascono dalla geometria euclidea del piano, attraverso i primi tre postulati

Tra due punti qualsiasi è possibile tracciare una ed una sola retta;

Si può prolungare un segmento oltre i due punti indefinitamente;

Dato un punto e una lunghezza, è possibile descrivere un cerchio;

Da cui risulta che le uniche operazioni ammesse sono le seguenti:

1) Dati due punti, tracciare la retta passante per essi

2) Dati due punti A e B, tracciare una circonferenza di centro A e passante per B

3) Determinare l'eventuale punto di intersezione di due rette

4) Determinare gli eventuali punti d'intersezione di una circonferenza con una retta

5) Determinare gli eventuali punti d'intersezione di due circonferenze

Non è invece ammissibile:

1) Applicare un segmento a una retta (ossia trasportarne la lunghezza) mediante la riga, in quanto essa non è graduata

2) Applicare un segmento a una retta mediante il compasso, in quanto i postulati non prevedono questo tipo di manovra

Le semplici operazioni eseguibili riescono, comunque, a risolvere gran parte di problemi geometrici molto più complessi; in particolare, con riga e compasso, è possibile costruire: dato un segmento AB, ed una semiretta di estremo C, un segmento CD sulla semiretta avente la stessa lunghezza di AB (trasporto di misura); data una retta, ed un punto esterno ad essa, una parallela passante per il punto; data una retta, ed un punto, una perpendicolare passante per il punto; dato un angolo α, ed una semiretta, un angolo, sulla semiretta, uguale ad α. Inoltre, è possibile bisecare un segmento; bisecare un angolo. Sono fattibili le quattro operazioni e perfino la radice quadrata.

In altre parole, un certo numero reale n  è costruibile se è costruibile (sempre con riga e compasso) un segmento avente lunghezza n (fissata, ovviamente un’unità di misura).

Ci vorranno molti secoli prima che si comprenda, attraverso la geometri analitica, che a problemi geometrici trattati solo con riga e compasso, corrispondono operazioni algebriche attuabili mediante operazioni razionali ed estrazioni di radice quadrate. In poche parole:

Condizione necessaria e sufficiente perché un problema sia risolubile con riga e compasso è che si possa tradurre in un problema algebrico risolubile per radicali quadratici attraverso un numero finito di operazioni razionali ed estrazioni di radici quadrate

Su queste basi è praticamente immediato comprendere che i tre grandi problemi già nati e affrontati prima di Euclide non potevano essere risolti: la trisezione di un angolo (non ammette radici razionali); la duplicazione del cubo (compare una radice cubica); la quadratura del cerchio (costruzione di un numero addirittura trascendente, come π).

Prima di analizzare in dettaglio questi tre problemi (e l’ultimo, in particolare, che ci riporterà al nostro pi greco), cerchiamo di prendere dimestichezza con la costruzione con riga e compasso, attraverso qualche esempio. Un gioco davvero divertente… ve lo assicuro (pensiamo anche a Napoleone e al fatto che per lui perfino la riga era di troppo…).

Cominciamo con tre costruzioni veramente facili da ottenere e molto didattiche: la determinazione del punto di mezzo di un segmento; il tracciamento, da un punto, di una perpendicolare a una retta;  la rappresentazione di un triangolo equilatero, a partire da una sua base. Stiamo bene attenti a non tradire i cinque punti elencati precedentemente.

In Fig. 4, a sinistra, abbiamo la situazione di partenza nel nostro piano euclideo: un segmento AB, di cui vogliamo determinare secondo le regole platoniche di geometria pura e non di meccanica, il punto medio.

N.B: Sia per questa costruzione che per quelle che seguiranno, sarebbe cosa interessante (e divertente) provare da soli, prima di guardare la figura di destra.

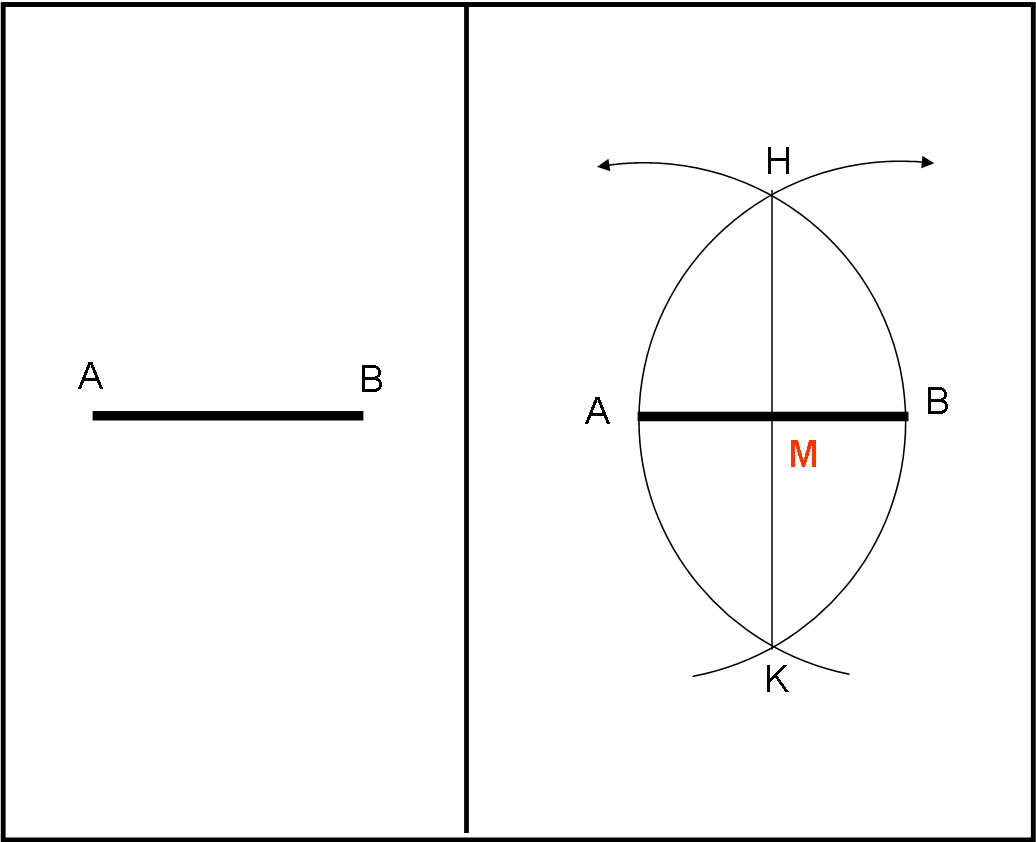
La nostra riga non è ovviamente graduata. Poco male… Prendiamo il compasso molle, facciamo centro in A, apriamolo fino a toccare B e descriviamo la circonferenza relativa. A questo punto il compasso si chiude automaticamente. Nessun problema… facciamo centro in B, lo apriamo nuovamente fino a toccare A e tracciamo il cerchio relativo. I due cerchi si incontrano nei punti H e K. Tracciamo, con la riga, la retta che passa per H e K. Essa incontra il segmento AB in M, che risulta essere il suo punto medio.

Ovviamente, bisognerebbe dimostralo… Spesso è estremamente facile, ma in certi casi, la dimostrazione può essere molto complessa e trattata "per assurdo" . Non dimentichiamo, tuttavia, che una cosa è costruire una nuova figura e un’altra è conoscere le caratteristiche delle figure e i teoremi relativi. Talete, Pitagora e lo stesso Euclide sapevano bene come usarli, avendoli dedotti rigorosamente.

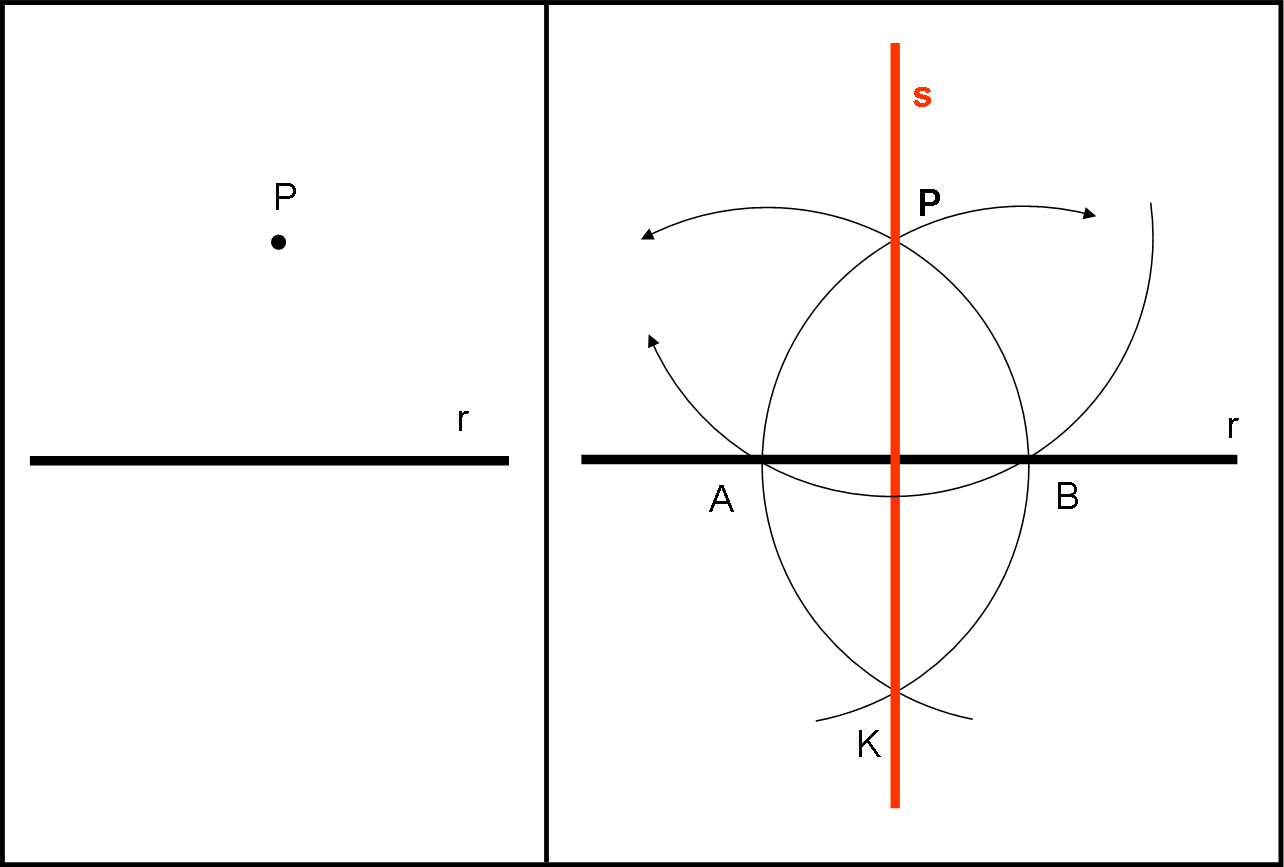
In Fig. 5, facciamo qualcosa di molto simile. Nella parte sinistra abbiamo le condizioni di partenza: una retta r e un punto P a lei esterno (ma potrebbe anche essere sulla retta). Dobbiamo tracciare la perpendicolare della retta, passante per P e perpendicolare a r. Facendo centro in P, apriamo il nostro compasso molle a piacere in modo che il cerchio che ne deriva intersechi la retta r in due punti A e B. In modo analogo a quanto fatto in Fig. 4, tracciamo le circonferenze con centro in A e B e raggio AP e BP in modo da ottenere il punto K. La retta che passa da P e da K è la perpendicolare richiesta.

In Fig. 6, consideriamo il segmento AB. Come nel caso di Fig. 4, tracciamo le circonferenze di raggio AB con centri in A e B. Si ottiene il punto C, intersezione tra di loro. Basta ora congiungere con la riga A on C e B con C. Il triangolo equilatero è servito.

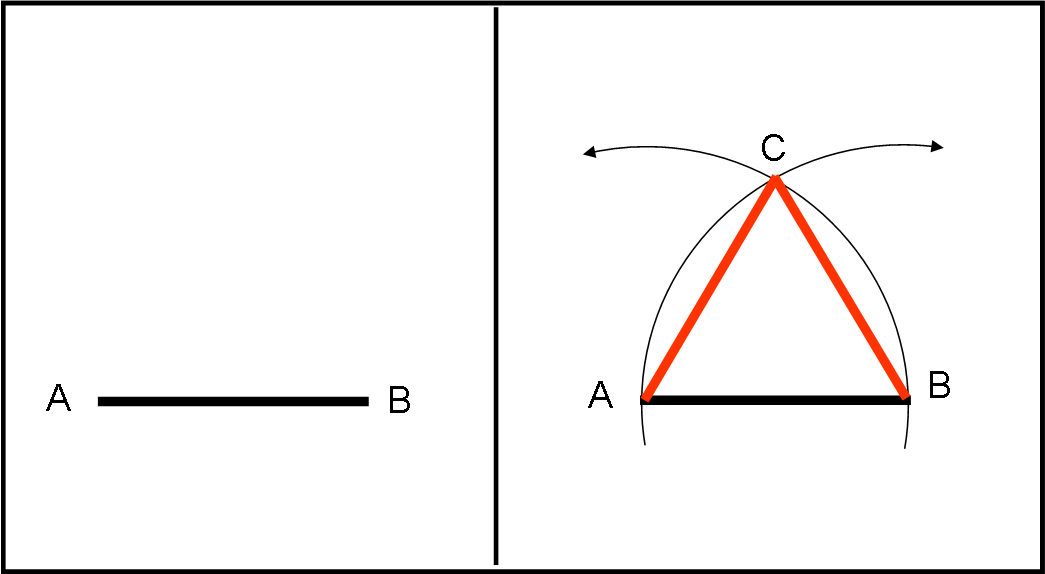
Anche se intuitivo, notiamo bene che abbiamo usato solo il compasso per tracciare cerchi allargandolo fino al punto desiderato (NON abbiamo misurato una distanza con il compasso e poi la abbiamo utilizzata per un’altra circonferenza) e abbiamo solo ricavato punti da intersezioni tra circonferenze e rette e circonferenze. Proprio conformemente ai cinque punti fondamentali.

Si potrebbero fare cento altre costruzioni più o meno complicate, ma ve ne è una veramente fondamentale ed estremamente utile per moltissime costruzioni di carattere ben più generale. Dato che il compasso è molle, NON potremmo direttamente portare un segmento AB qualsiasi su una retta r: sarebbe, infatti necessario o avere una riga graduata o poter fermare l’apertura del compasso. Cose assolutamente vietate. Se, però, trovassimo un metodo puramente geometrico per tale trasporto, lo potremmo usare in qualsiasi occasione e, conseguentemente, anche il trasporto di un segmento su una retta diventerebbe operazione ammessa (malgrado sia sempre basata su un certo numero di operazioni). Non ci resta, quindi, che mostrare queste operazioni… (mi raccomando, provate anche da soli…).

La configurazione di partenza si vede nella Fig. 7, a sinistra. Abbiamo una retta r  e un segmento AB, qualsiasi, nel piano euclideo. Scegliamo un punto C qualsiasi della retta e cerchiamo di trasportare il segmento AB sulla retta facendo coincidere A con C.

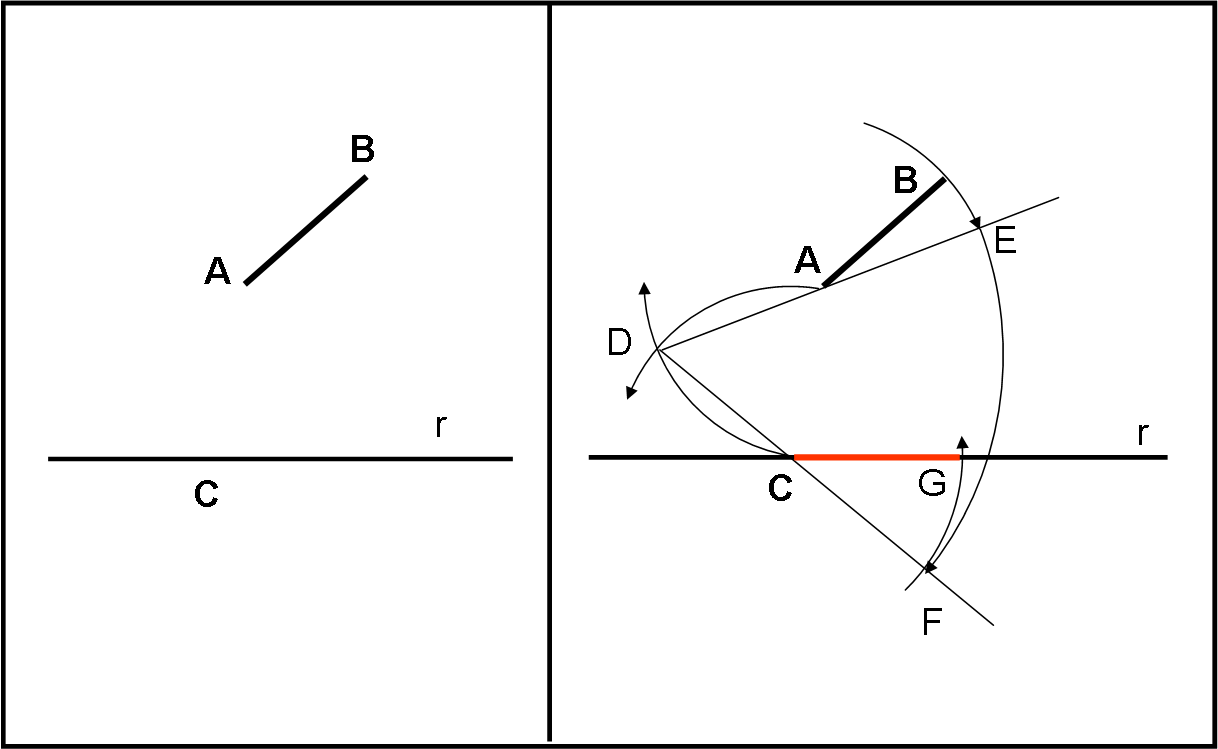
Con centro in C tracciamo la circonferenza con apertura di compasso uguale a CA. Con centro in A tracciamo la circonferenza con apertura di compasso uguale ad AC. L’intersezione tra queste due circonferenze è il punto D. Tracciamo la retta che passi per D e per A. Con centro in A tracciamo la circonferenza di apertura (possiamo chiamarlo raggio) AB fino a incontrare la retta precedente in E.

Ovviamente, per come è stato costruito, AB = AE. Tracciamo la retta DC. Con centro in D tracciamo la circonferenza di raggio DE fino a incontrare la retta DC in F. CF è uguale ad AE. Tracciamo, infine, la circonferenza di centro C e raggio CF, trovando il punto intersezione G con la retta r. Il segmento CG è uguale al segmento AB. Abbiamo trasportato quest’ultimo sulla retta nel punto voluto senza misurarne la lunghezza e senza bloccare il compasso, operazioni impossibili.

D’ora in poi potremmo considerare il trasporto di un segmento come operazione consentita dalle regole, sapendo come effettuarla di volta in volta.

Aggiungiamo subito anche le operazioni da svolgere per ottenere la parallela, passante per C, a una retta r.  Scegliamo due punti qualsiasi sulla retta r e siano A e B (Fig. 8).

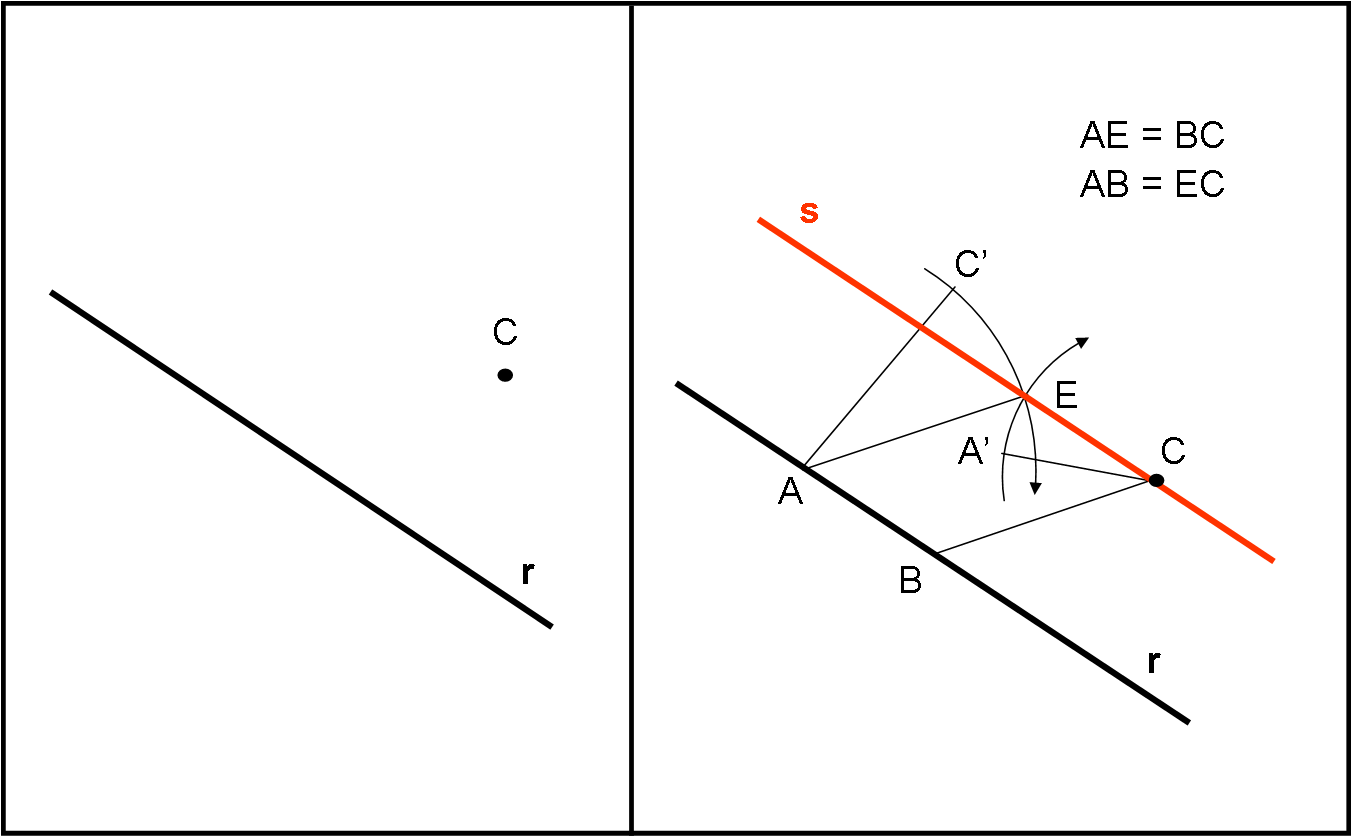
Sappiamo ormai trasportare un segmento AB in qualsiasi altra posizione. Portiamolo, ad esempio, in C e sia CA’. Tracciamo la circonferenza di centro C e raggio CA’. Trasportiamo ora il segmento BC in A e sia AC’. Tracciamo la circonferenza di centro A e raggio AC’. Le due circonferenze si intersecano nel punto E. Tracciamo la retta s passante per E e per C: essa è la parallela a r passante per C. Si dimostra facilmente notando che il quadrilatero AECB ha i lati opposti uguali (per costruzione) e, quindi, risulta essere un parallelogramma, da cui segue che EC è parallelo ad AB. Ovviamente, esistono vari modi per costruire la stessa figura finale e potete divertirvi a provare (ricordando, però, di seguire le regole della Scuola di Platone!)

A questo punto, le operazioni geometriche possono permettere di eseguire le quattro operazioni (somma, sottrazione, moltiplicazione e divisione). Va comunque introdotto un segmento unitario, scelto a piacere  al quale riferire tutti gli altri segmenti.

Iniziamo a sommare e sottrarre due segmenti AB e CD, qualsiasi sia la loro posizione nel piano euclideo: ormai sappiamo come trasportarli su una certa retta nel punto prescelto. Usiamo la Fig. 9.

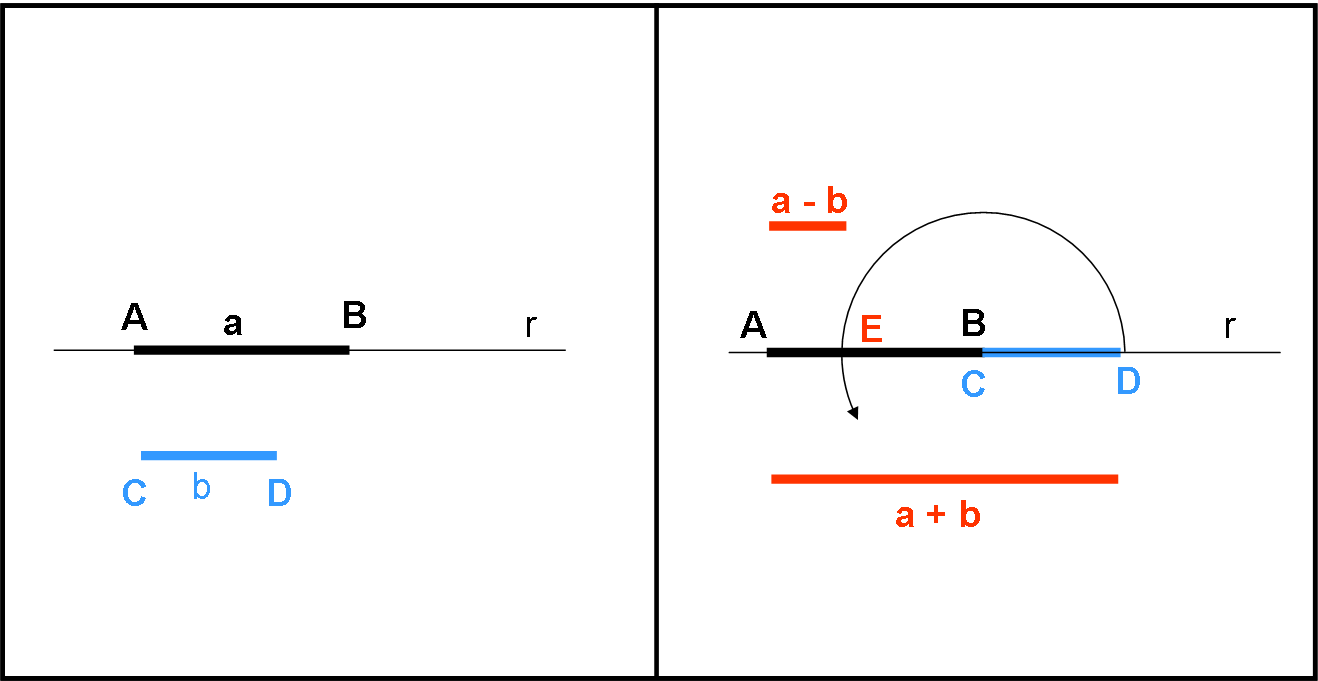
Consideriamo la retta r che contenga il segmento AB che misura a unità. Separatamente abbiamo un segmento CD che misura b unità. Ormai non abbiamo più nessun problema a trasportare il segmento CD sulla retta r facendo coincidere C con B. Con centro B = C, tracciamo la circonferenza di raggio CD fino a intersecare la retta r in E. Il segmento AE non è altro che la differenza tra a e b. Mentre il segmento AD non è altro che la somma di a e b.

Non è  nemmeno difficile eseguire la moltiplicazione e la divisione di due segmenti di misura a e b. Utilizziamo la stessa figura per entrambe le operazioni, ma è ovvio capire che potevano cambiare rette senza nessun problema. In Fig. 10 moltiplichiamo il segmento AB (di misura a) per il segmento CD (di misura b).

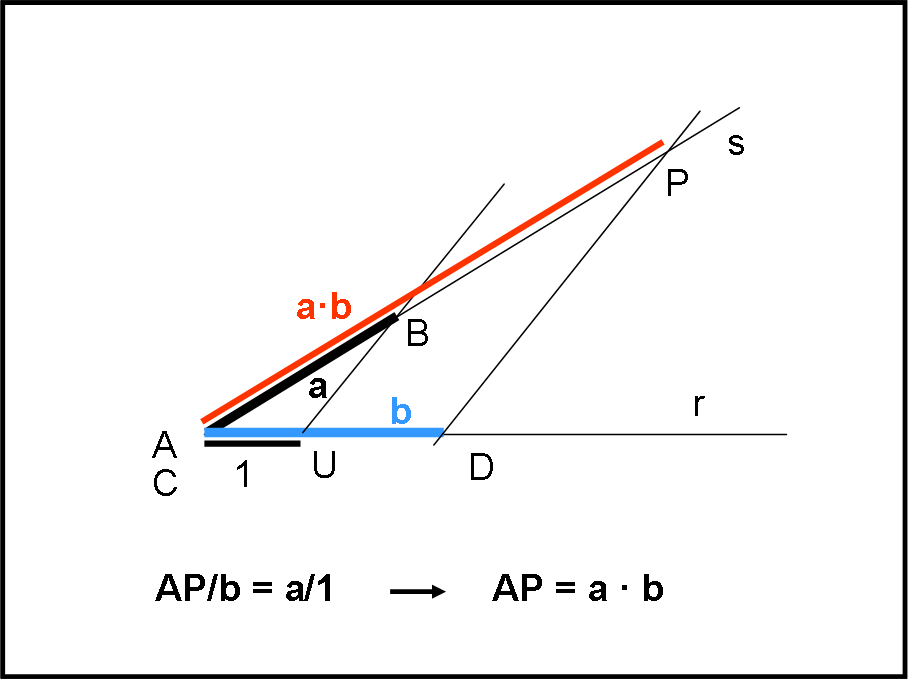
Portiamo il segmento a sulla retta s passante per A. Portiamo il segmento b (CD) sulla retta r, anche lei passante per A. Facciamo coincidere C con A. Riportiamo l’unità AU (1) sulla retta r, partendo ancora da A. Tracciamo la retta BU e la retta DP, parallela a BU (sappiamo che è possibile farlo). Conosciamo perfettamente le caratteristiche dei triangoli simili, per cui possiamo considerare i due triangoli ABU e APD e scrivere la proporzione:

AP/AB = AD/AU

Inserendo le misure:

AP/a = b/1

Ossia:

AP = a · b

Il segmento AP rappresenta geometricamente il prodotto di AB per CD.

Analoga operazione per la divisione di AB (a) per CD (b) in Fig. 11.

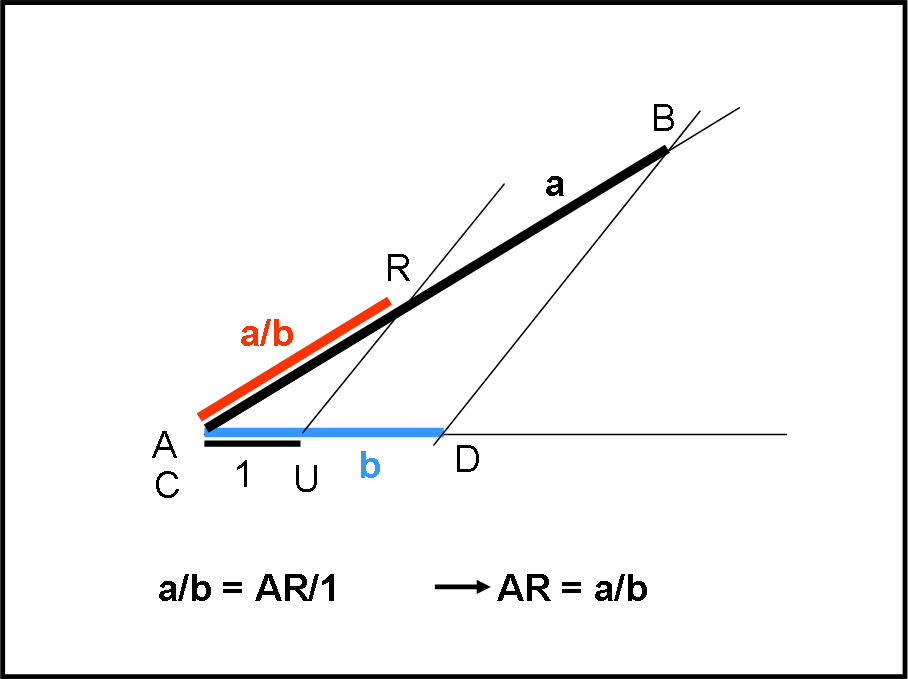
Riportiamo i segmenti AB su s e CD su r con A coincidente con C. Su r riportiamo anche l’unità (AU). Tracciamo la retta DB e la sua parallela UR. Dai soliti triangoli simili, possiamo scrivere:

AR/AU = AB/CD

Ossia:

AR = a/b

Il segmento AR rappresenta il rapporto tra AB e CD.

Particolarmente importanti sono le operazioni da svolgere per ottenere la radice quadrata di un numero. In particolare, troveremo la radice quadrata di 2, un numero di grande interesse, dato che è anch’esso irrazionale, ma è algebrico, ossia è soluzione di un polinomio a coefficienti razionali. Del tutto diverso da pi greco. Detto in parole “antiche”, √2 è COSTRUIBILE con le regole ideali della geometria platonica ed euclidea, mentre π NON lo è.

 

Euclide andava a nozze con questa costruzione, dato che si basava sul suo secondo teorema: Il quadrato costruito sull’altezza relativa all’ipotenusa di un triangolo rettangolo è equivalente al rettangolo che ha per lati le proiezioni dei cateti sull’ipotenusa.

Consideriamo la Fig. 12.

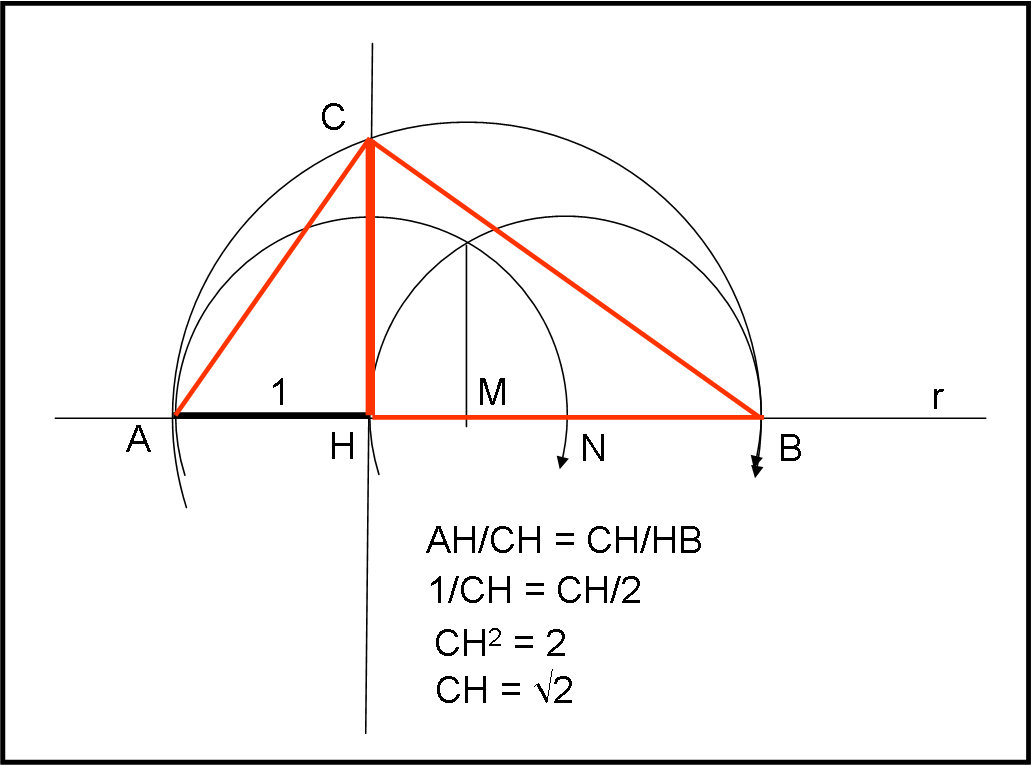
Come al solito, impostiamo l’unità di misura uguale a 1. Chiamiamola AH e impostiamola sulla retta r. Da H tracciamo la circonferenza di raggio uguale a 1(AH) fino a determinare N. Con centro in N e raggio uguale a NH si ottiene B. Siamo ormai capaci di determinare il punto medio di AB e chiamiamolo M. Con centro in M e raggio uguale a MA tracciamo una circonferenza. Dal punto H tracciamo la perpendicolare ad AB (tutte operazioni costruibili) e sia C il punto d’intersezione con la circonferenza di centro M. Uniamo C con A e con B. Il triangolo ACB è rettangolo (l’angolo in C è retto dato che è relativo a un diametro del cerchio). Non ci resta che applicare il secondo teorema di Euclide al triangolo ABC:

CH² = AH · HB

Ossia:

CH² = 1 · 2     (HB è , per costruzione, il doppio dell’unità)

CH = √2

Per comprendere ancora meglio quanto Euclide sia riuscito a raggiungere attraverso mezzi apparentemente irrealistici e ideali, basta considerare due dei suoi innumerevoli enunciati. Il primo (proposizione 4) ci porta alla definizione di quadrato di un binomio e il secondo (proposizione 5) ad un celeberrimo prodotto notevole.

Il primo dice: “Se si divide a caso una linea retta, il quadrato di tutta la retta è uguale alla somma dei quadrati delle parti e del doppio del rettangolo compreso dalle parti [stesse].”

Esso può essere tradotto nella Fig. 13:

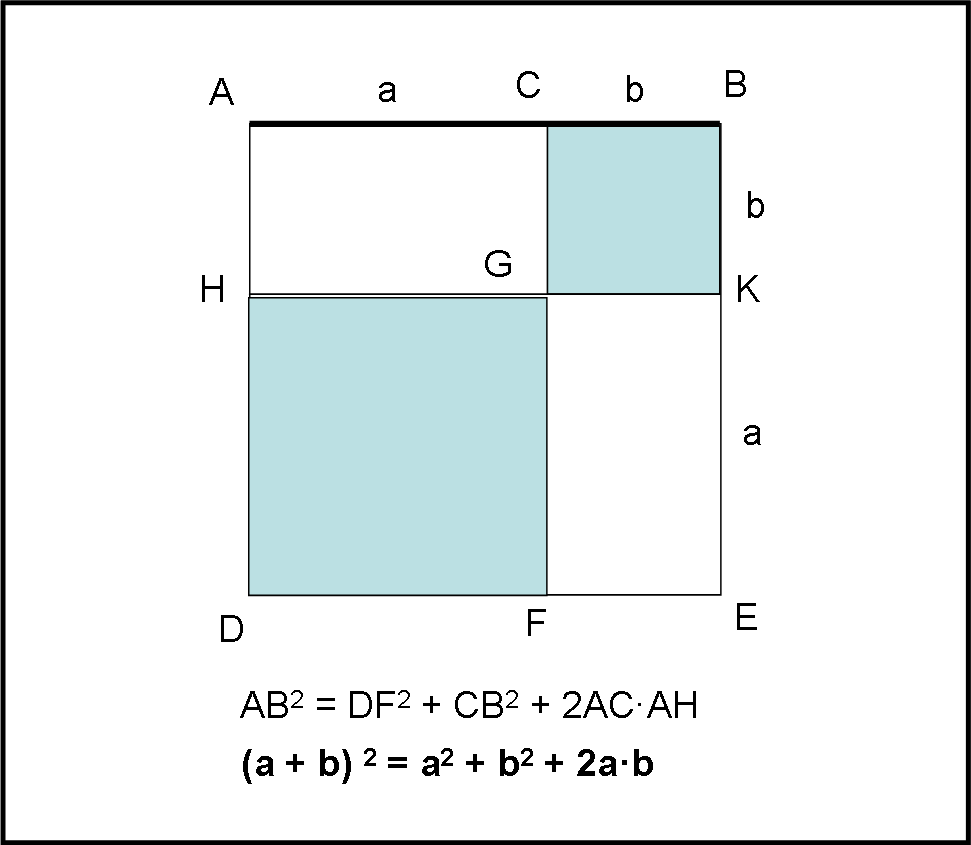
La retta è il segmento AB, che viene divisa in modo qualsiasi (ad esempio dal punto C).

L’enunciato dice che:

AB² = DF² + CB² + 2AC· AH

Chiamando AC = a e CD = b, si ottiene:

(a + b)² = a² + b² + 2 ab

Che è proprio il quadrato di un binomio.

Ancora più affascinante è la proposizione 5, che recita: “Se si divide una retta in parti uguali e disuguali, il rettangolo compreso dalle parti disuguali della retta, insieme col quadrato della parte compresa fra i punti di divisione, è uguale al quadrato della metà della retta.”

 Vediamo la Fig. 14:

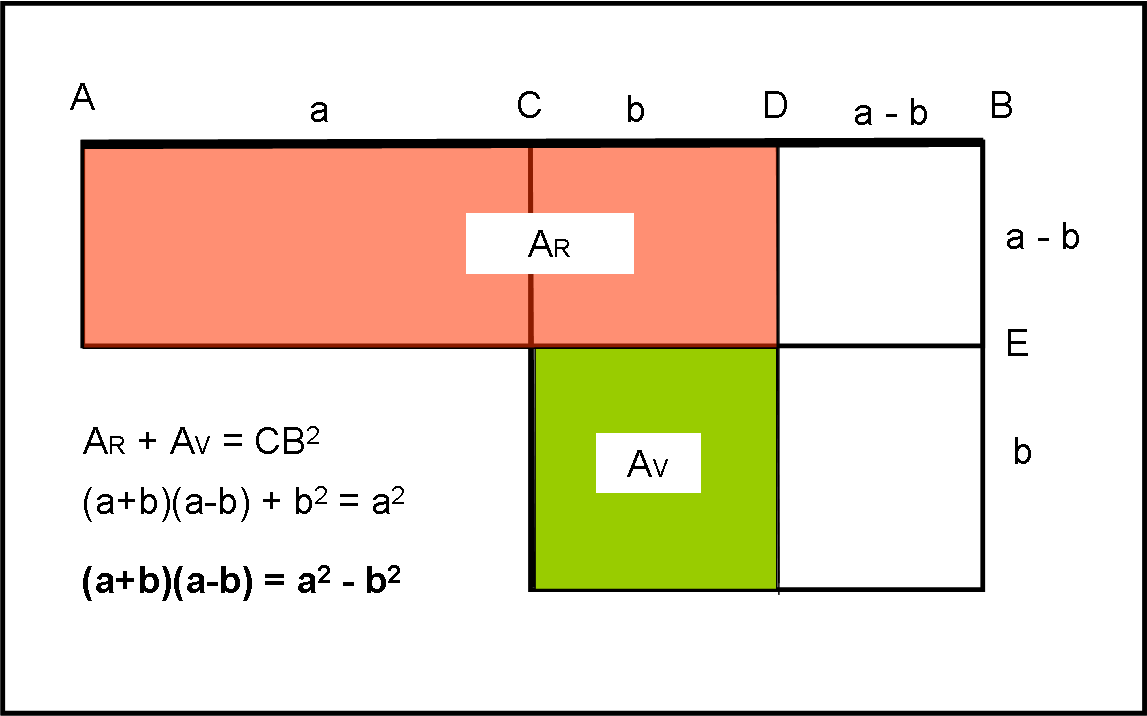
La retta AB viene divisa a metà attraverso C e in parti non uguali attraverso D. L’enunciato diventa, perciò:

A_rossa + A_verde  = CA² = CB²

 AD·DB + CD² = CA² = CB²

Notando che DB = DE e ponendo AC = a e CD = b, si ha che DB = DE = a – b, mentre AD = a + b

Sostituendo si ha:

(a + b)(a – b) = a² – b²

Uno dei più importanti prodotti notevoli!

Possiamo ripetere un concetto fondamentale e di portata enorme. Solo la geometria analitica e l’algebra sono riuscite a dare spiegazioni rigorose delle caratteristiche di numeri particolari, ma una serie di regole basate su qualcosa dall’apparenza più filosofico che scientifico erano già riuscite a prevedere (senza spiegare) tutto ciò che avrebbe avuto ancora bisogno di secoli per essere dimostrato. L’equivalenza tra numeri “costruibili” e operazioni algebriche lascia ancora esterrefatti e ammirati… Euclide e i suoi colleghi avevano fatto un lavoro a dir poco eccezionale, utilizzando solo la "pura" geometria platonica.

Bene, ci siamo costruite le basi per capire cosa sia considerato costruibile e cosa non lo sia (ma i lavori di Euclide andrebbero ripresi e "degustati" più a lungo). Possiamo tornare indietro nel tempo e affrontare i problemi che apparivano (e che erano) impossibili. Oggi sappiamo anche perché (radici cubiche e numeri trascendenti non algebrici), ma è veramente interessante descrivere come i tre grandi problemi ricordati precedentemente siano, comunque, risolvibili, con operazioni meccaniche non riconducibili alle regole puramente geometriche. Nascono curve nuove che, non essendo circonferenze, rendono i risultati non ACCETTABILI, ma ci rivelano un mondo geometrico fantastico, di cui pi greco resta l’attore principale.

 

QUI gli altri articoli dedicati all'infinita storia del pi greco