Questo articolo nasce come appendice  a quello sulle  varietà topologiche.  Non è proprio banale costruire un atlante per una varietà topologica. Per cui  voglio fare un esempio "pratico", usando una varietà unidimensionale; Il cerchio  è infatti una varietà topologica di dimensione 1.La scelta ovviamente è per comodità grafica e di notazioni.

Riprendiamo la definizione di varietà topologica:

"Uno spazio topologico X si dice localmente euclideo se ogni suo punto x ha un intorno aperto Ui  omeomorfo a un disco aperto  in .  Chiamiamo ;

"Uno spazio topologico connesso , di Hausdorff, e localmente euclideo  si dice varietà topologica."

".. la coppia ( ,) si chiamo carta e l'insieme di tutte le carte   si chiama atlante."

Ricopriamo il cerchio con degli archi aperti

Consideriamo un cerchio unitario, di equazione . Dobbiamo cercare degli aperti sul cerchio, la  la cui unione dia il cerchio , e per ciascuno dei quali   esiste un  omeomorfismo in un aperto di R,  ovvero in un un intervallo aperto. Ricordo , che per quanto visto nell'articolo sulla topologia indotta,  gli aperti del cerchio sono archi di cerchio.

 

Il cerchio non è omeomorfo ad un segmento. Quindi non possiamo usare il cerchio stesso.Se spezziamo il cerchio in quanti si voglia archi aperti, ci resteranno sempre dei buchi. Dobbiamo quindi sovrapporre più archi aperti e farne l'unione. Tale unione non sarà disgiunta; poco importa. Quello che serve è che ogni punto sia coperto.

Proviamo così:

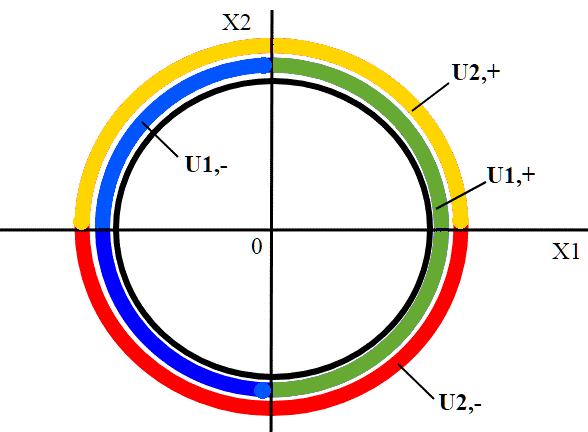
In questo modo tutti i punti del cerchio sono contenuti da qualche arco.

(N.B. Questa chiaramente non è l'unica soluzione possibile.)

Chiamiamo il nostro cerchio. Formalmente gli Ui sarebbero così definiti:

.

Dobbiamo ora definire le  ; proiettiamo i quattro archi sugli assi in questo modo:

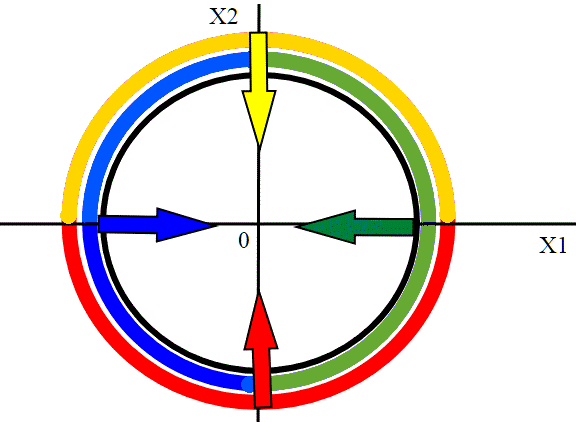
Per esempio, la proiezione dell'arco giallo e di quello rosso  è l'intervallo (-1,1) sull' asse x1.

  ,

, 

mentre  la proiezione dell'arco verde e di quello blue è l'intervallo (-1,1) sull' asse x2.

 , 

, 

Il fatto che il punto immagine sia un punto del piano, può trarre  in inganno; in realtà l'immagine di una qualsiasi delle  è un segmento, con una sola coordinata. Le quattro coppie Ui, formano dunque un atlante del cerchio. A questo punto avremmo finito. Ma approfittiamo di questo esempio abbastanza semplice, per introdurre il concetto di cambiamento di carta, definiamo cioè le cosiddette funzioni di transizione. Vediamo di collegare con una funzione le coordinate dei punti comuni alle due carte.

Consideriamo l'intersezione fra due archi di cerchio che compongono l'atlante, quello giallo e quello verde:

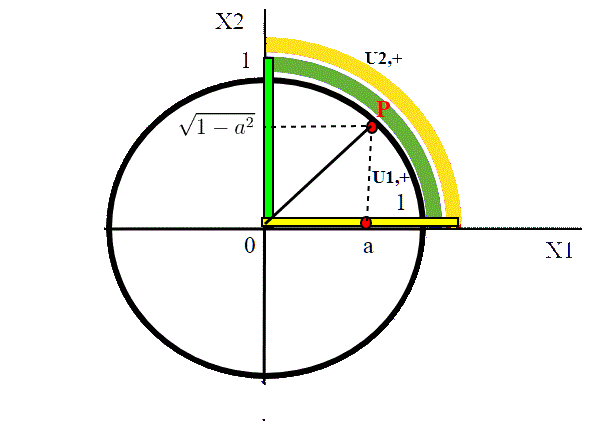è rappresentata dal quarto di cerchio con x1,x2>0. Entrambi gli omeomorfismi hanno come immagine l'intervallo aperto (0,1), posizionato diversamente nel piano, colorato in verde e giallo. Quello che succede, è che un punto P appartenente a questa intersezione, viene mappato diversamente nelle due carte. Se in un intervallo la coordinata è a, nell'altro (teorema di Pitagora) è .  Ci interessiamo adesso proprio a questo cambio di coordinate. Consideriamo un a qualsiasi, o<a<1, situato nell'intervallo giallo, che è l'immagine di  tramite ;

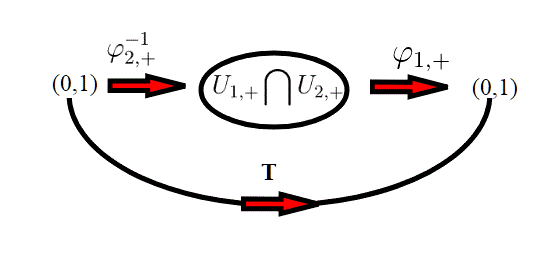
se consideriamo l'applicazione inversa  andiamo su , e poi tramite   otteniamo:

, cioè eseguiamo il cambio di coordinate.Se chiamiamo T questa funzione composta,

T:(0,1)--->(0,1) allora:

.

Tale funzione prende il nome di funzione di transizione, ed è chiaramente un omeomorfismo. Infatti è composizione di funzioni biunivoche e continue.

Osserviamo che in(0,1), la funzione T è derivabile:., in particolare in (0,1) ammette retta tangente in ogni punto. Dunque T è .

A cosa servirà tutto questo discorso? Ad introdurre la varietà differenziabili. Un punto d'incontro fra la topologia e l'analisi matematica. Ma prima dobbiamo chiarire bene il concetto di differenziale.

1):Questa affermazione è per chi conosce il differenziale di una funzione.