Matematizziamo il nastro di Möbius ,parte 7°:un teorema necessario.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Nell'articolo precedente, abbiamo realizzato un primo esempio di Spazio quoziente. Chi vuole riprendere il discorso da lì,può visualizzare l'esempio. Chi invece non lo ritenga necessario, può andare avanti direttamente.
Una definizione alternativa di continuità.
La definizione di continuità che abbiamo dato qui , era la seguente:
Una funzione f: X-->Y fra due spazi topologici è continua se per ogni aperto A di Y, è un aperto di X.
alternativamente, invece di usare gli aperti, si possono usare gli insiemi chiusi:
Una funzione f: X-->Y fra due spazi topologici è continua se per ogni chiuso C di Y, è un chiuso di X.
Per dimostrare questa affermazione, basta notare questa proprietà delle controimmagini, puramente a livello insiemistico:
Se T è un sottoinsieme di X, f una funzione qualsiasi di f:X--->Y, allora vale la seguente eguaglianza:
. Ricordo che se T è un sottoinsieme di Y, il complementare è Y\T.
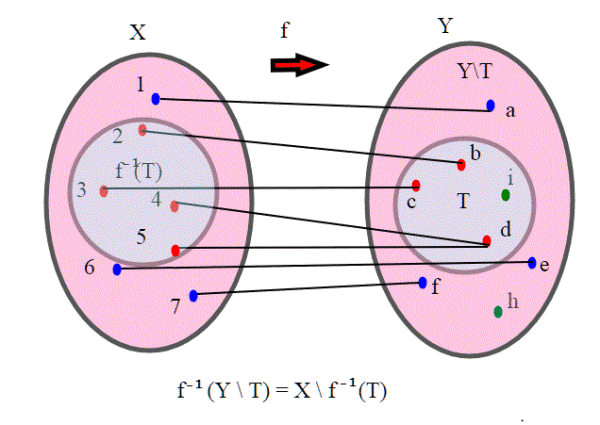
Infatti, se vale tale eguaglianza, se C è un insieme chiuso, allora Y\C è aperto; Quindi è aperto, ma allora , anche
è aperto, di conseguenza
è chiuso. Analogamente si può dimostrare il viceversa.
Definizione di funzione aperta (o chiusa)
Una funzione f : X → Y tra spazi topologici si dice aperta se per ogni aperto A ⊆ X, f(A) ⊆ Y `e aperto.
Una funzione f : X → Y si dice chiusa se per ogni chiuso C ⊂ X, f(C) `e chiuso in Y .
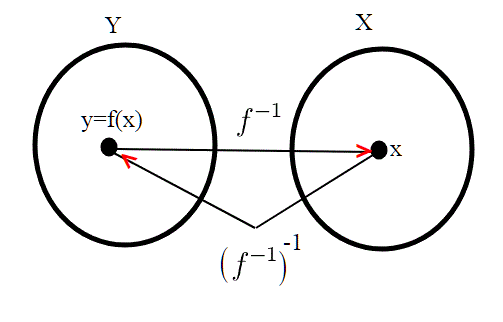
Le funzioni inverse; proprietà.
Per chi non ha ben chiaro il concetto di funzione inversa, e in particolare il fatto che qualsiasi sia x, richiamo alcune proprietà. Chi vuole può fare a meno di leggere tale proprietà, e continuare tranquillamente la lettura.
Un altra definizione di omeomorfismo.
In questo articolo, abbiamo dato la definizione di omeomorfismo:
" Una funzione f: X--->Y fra spazi topologici è un omeomorfismo se f è continua, biettiva e la sua inversa : Y → X è anch'essa continua."
Una definizione equivalente è questa:
Una funzione f : X → Y tra due spazi topologici è un omeomorfismo se e solo se f è continua,biettiva e aperta (oppure chiusa).
In pratica, sotto queste condizioni, dobbiamo dimostrare che anche è continua. Sappiamo che qualsiasi sia
,
;
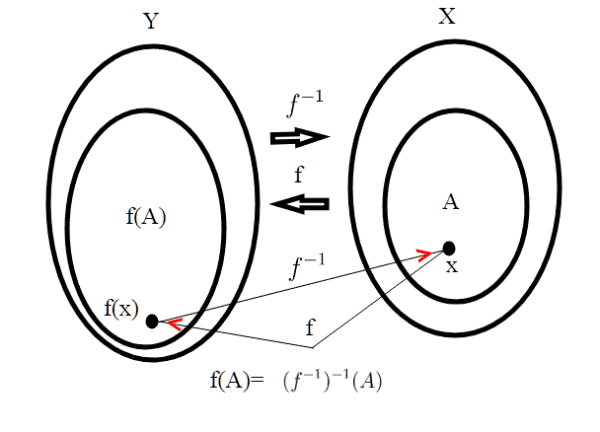
Supponiamo f aperta; quindi per ogni sottoinsieme A ⊆ X aperto, si ha che:
Quindi `e continua se e solo se f è aperta,ovvero se l'immagine di ogni aperto tramite f è un aperto.
Supponiamo f chiusa, e consideriamo un chiuso :
.
Quindi `e continua se e solo se f è chiusa,ovvero se l'immagine di ogni aperto tramite f è un aperto.
Spazi compatti.
Richiamo la definizione di spazio compatto, che abbiamo dato qui:
"... dato uno spazio topologico S,per dire se S è compatto dobbiamo verificare , per ogni una famiglia di aperti Ui tale che la loro unione dia S, se questo riusciamo a realizzarlo con un numero finito di questi aperti. Dunque uno spazio topologico è compatto se ammette un sottoricoprimento finito, per ogni ricoprimento aperto." Sempre nelle stesso articolo, è spiegato per esteso cos'è un ricoprimento. Vedremo ora due importanti teoremi sugli spazi compatti.
a) Un sottoinsieme chiuso C di uno spazio compatto X è uno spazio compatto (con la topologia indotta).
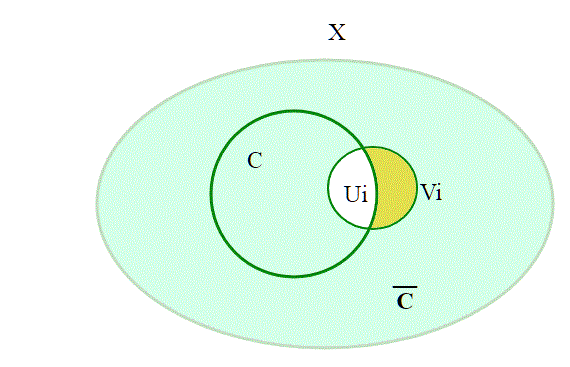
Sia U = un ricoprimento aperto di C; poichè C ha la topologia indotta,
, con Vi aperto di X.
(dove
è il complementare di C che quindi è aperto essendo il complementare di un chiuso) è un ricoprimento aperto di X; poichè X è compatto è possibile estrarre un sottoricoprimento finito
; allora
è un sottoricoprimento finito di U.
b) Sia f : X--->Y un’applicazione continua, e sia X uno spazio compatto. Allora f(X) è uno spazio compatto.
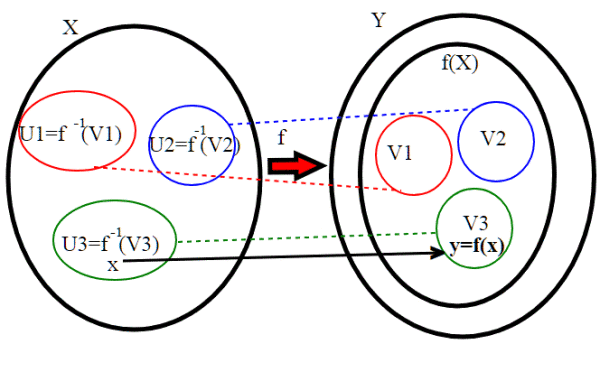
Sia un ricoprimento aperto di f(X); essendo f continua
è un ricoprimento aperto di X. Ma X è uno spazio compatto, quindi ammette un sottoricoprimento finito,
Ma allora è un sottoricoprimento finito di V; infatti preso un y qualsiasi in f(X), esiste un
tale che y=f(x). X è tutto ricoperto dagli Uj, quindi
per qualche k. Di conseguenza
. Quindi anche f(X) è compatto.
c) (Compatto di Hausdorff) Un sottoinsieme compatto K di uno spazio di Hausdorff X è un sottoinsieme chiuso.
Abbiamo di recente definito gli spazi di Hausdorff;
Uno spazio topologico S è detto di Hausdorff se per ogni coppia x, y di elementi distinti di S esistono un intorno di x e un intorno di y disgiunti. In tal caso lo spazio si dice separato.
Ma veniamo alla dimostrazione; per dimostrare che K è chiuso basta dimostrare che il suo complementare in X, , è aperto.
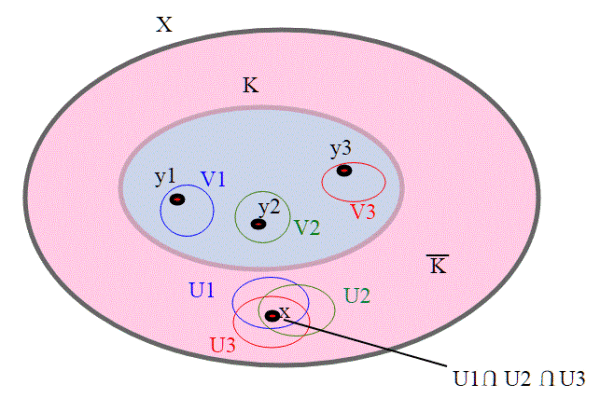
Consideriamo un punto x qualsiasi, . Se riusciamo a trovare un aperto che lo contiene, allora x è un punto interno a
, quindi essendo x qualsiasi,
è aperto. K è compatto; esiste allora un ricoprimento di Vy aperti . Per ciascun Vy, visto che x è distinto da ogni punto y di K,, ci sarà un corrispondente Uy che contiene x , ma disgiunto da Vy. Essendo k compatto, ammette un sottoricoprimento finito. Sia V1,V2,...Vn un tale ricoprimento. Siano U1,U2,..Un degli aperti corrispondenti; tutti contengono x. Pertanto
è un aperto e contiene x, ed è anche disgiunto da K, ovvero
. Pertanto x è interno a
, che quindi è aperto, e K che è il complementare è chiuso.
Eccoci arrivati al nostro teorema:
Sia f : X -->Y un’applicazione continua e biunivoca. Se X è compatto e Y è di Hausdorff allora è un omeomorfismo.
Per dimostrarlo, sfruttiamo i risultati precedenti.
Riportiamo quanto detto sopra riguardo agli omemorfismi:
Una funzione f : X → Y tra due spazi topologici è un omeomorfismo se e solo se f è continua,biettiva e aperta (oppure chiusa).
Ci basta quindi dimostrare che f è chiusa. Sia C un chiuso di X;
a) C è chiuso in X compatto, quindi C è compatto.
b) L'applicazione f è continua, quindi f(C) è compatto in Y.
c) Poichè Y è di Hausdorf, f(C) è chiuso.
bene, abbiamo già finito.


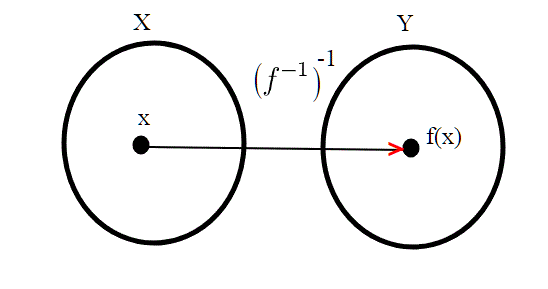




2 commenti
Esattamente un anno fa, ho pubblicato il quiz "art attack" ( di cui non fornisco il link, suggerendovi invece una ricerca con argomento "moebius" per avere una visione più ampia).
Grazie Maurizio. L'ho tirata un po' lunga per introdurre tutti gli elementi necessari ad una comprensione globale degli spazi quoziente. Altrimenti correvo il rischio di fare quello che fanno tutti. Con il risultato di quest'articolo siamo in grado di affrontare le superfici come cilindro, nastro ,toro, sfera sia da punto di vista astratto (topologia quoziente) sia nella rappresentazione analitica nello spazio Euclideo, e vedere che stiamo parlando della stessa cosa (con gli omeomorfismi). Il tutto dal prossimo articolo. So che ci sono state cose noiose da leggere, ma il divertimento comincia adesso.