Per questo breve articolo ringrazio il caro lettore Giovanni che, giustamente, in un commento ha evidenziato quanto sia, generalmente,  poco citata l'invarianza delle aree nello spaziotempo di Minkowski. Una lacuna che ci conduce a un semplice gioco essenzialmente geometrico.

Consideriamo in Fig. 1 un'asta rigida nera AB di lunghezza Lo= 1, che si trova in un sistema considerato in quiete. Un'altra asta rigida, della stessa lunghezza propria Lo= 1 (CD) si muove rispetto alla prima con velocità relativistica v. Ovviamente, la sua lunghezza propria deve essere misurata nel suo sistema di riferimento ed è quindi rappresentata da CD. Non pensiamo minimamente di misurare segmenti del secondo sistema con unità di misura del primo sistema e poi confrontarli, mi raccomando! In particolare se misuro CD con una squadretta lo trovo più lungo di  AB  misurato con la stessa squadretta. Le unità non si mantengono dato che lo spaziotempo di Minkowski non è proprio euclideo...

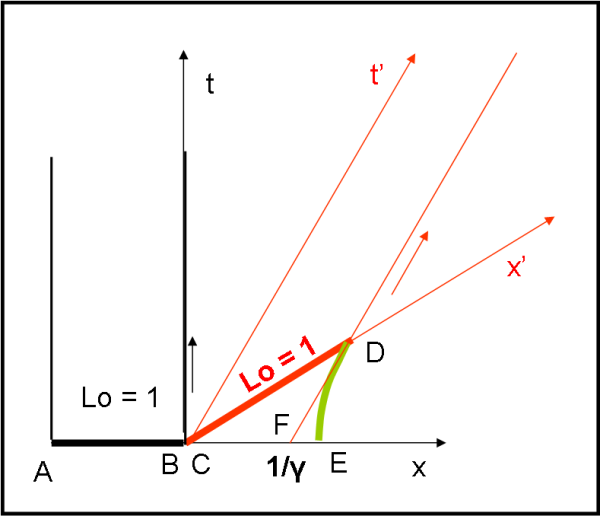
All'istante t = 0 si ha anche t' =0. Disegnando in verde l'iperbole di calibrazione possiamo stabilire che CE = 1 (CE è misurato con l'unità di misura del primo sistema) e CF = 1/ϒ. Non abbiamo fatto altro che mostrare la contrazione delle lunghezze dell'asta rossa rispetto al sistema in quiete.

Al tempo t1 = 1, disegniamo la situazione nello spaziotempo in Fig. 2.

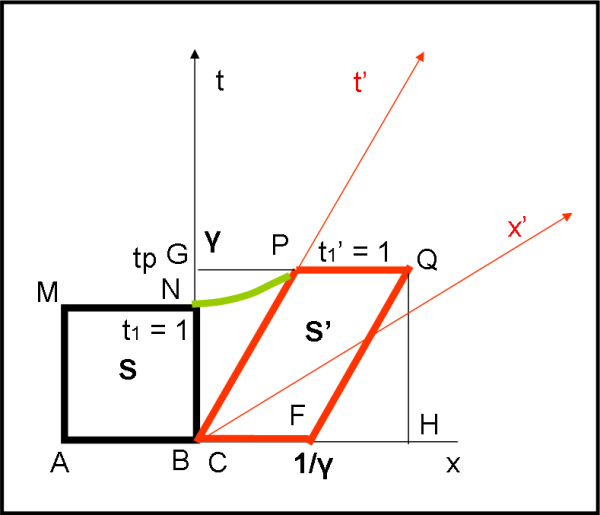
Il punto B si è portato in N. C si porta in P nel tempo t1' = 1. Vi è stata, ovviamente, la dilatazione dei tempo e per il sistema in quiete t_P= ϒ. L'area S spazzata dall'asta nera  è  quella del quadrato ABMN,  S = 1 ⋅ 1 = 1. L'area S' del parallelogramma rosso CFQP è quella dell'asta rossa relativa al sistema in quiete. La sua base CF è 1/ϒ, mentre la sua altezza è QH = GB = ϒ. Ne segue che l'area spazzata dall'asta rossa, per il sistema in quiete, non è altro che CF ⋅ QH = (1/ϒ) ⋅ϒ = 1. Le due aree sono, perciò uguali! Tanto si guadagna nel tempo e tanto si perde nella lunghezza.

Tuttavia, basta spostare, in Fig. 3, il triangolo CTF e portarlo in PQR, per poter dire che l'area spazzata dall'asta unitaria nel sistema in quiete, in una sua unità di tempo, è uguale all'area spazzata dall'asta unitaria nel sistema in moto, in una sua unità di tempo.

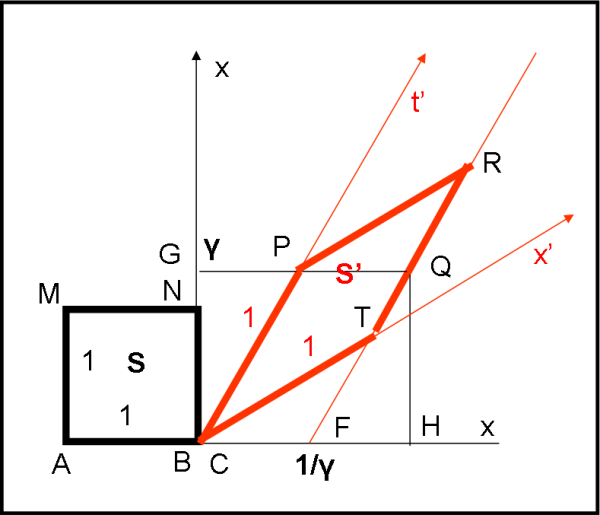
Il risultato, precedente, deve essere lo stesso mettendosi nel sistema di riferimento  in moto (asta rossa). Disegniamo la Fig. 4.

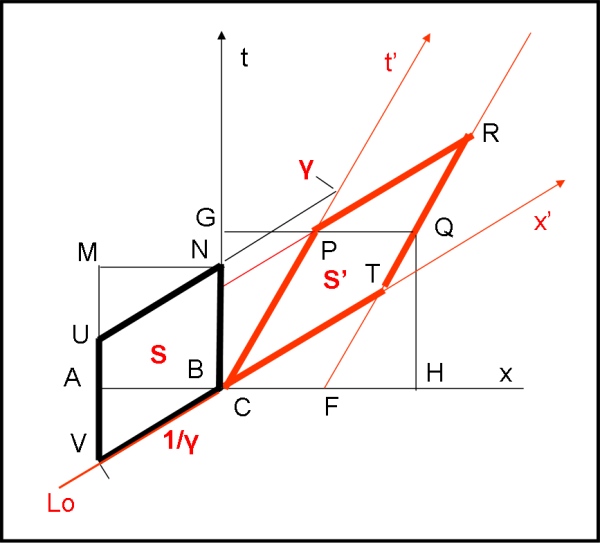
Sappiamo già che la stessa area unitaria di CFQP è uguale a quella del parallelogramma CPRT. Non ci resta adesso che disegnare il quadrato ABMN relativo al sistema in movimento. Basta tracciare le linee di simultaneità da N e B e ABMN diventa UNVC (si notano molto bene la contrazione della lunghezza e la dilatazione del tempo ed è facile indicare ϒ e 1/ϒ  relativi al sistema  in moto ). Ma ABMN è uguale a UNVC, data l'uguaglianza dei triangoli UMN e ABV. Ne consegue che l'area di CPRT è uguale  all'area di UNVC, ovvero S = S'

Le aree rimangono le stesse sia misurandole in un sistema che nell'altro. I lati cambiano lunghezza usando la stessa squadretta, ma l'area rimane la stessa (gli angoli non sono più retti e tanto si allunga un lato e tanto si accorcia l'altezza).

Ho cercato di rendere il più semplice possibile la trattazione e il concetto di fondo. Se Paolo o Giovanni o chiunque altro trovasse un sistema ancora più semplice e chiaro, lo dica apertamente e potremo migliorare l'articolo. Il nostro è un Circolo aperto a tutti e basato sul motto: collaborare per migliorare.