Matematizziamo il nastro di Möbius ,parte 9°: Il toro .***
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
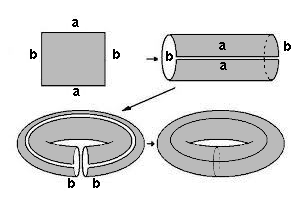
Adesso che stiamo prendendo mano con la topologia quoziente, cominciamo a costruire superfici un po' più complicate. Fino ad ora abbiamo incollato solo due dei quattro lati del quadrato, ottenendo delle figure "aperte". Vogliamo provare ad incollarli a due a due.Iniziamo a costruire un toro, che avete visto molto bene negli articoli di Arturo. Partiamo sempre dalla nostra striscia,anche questa volta quadrata ,
Lo schema della costruzione è questo:
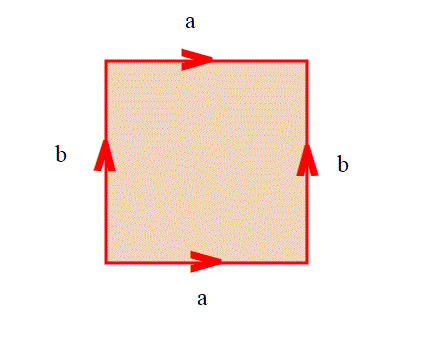
Dapprima incolliamo i due lati a, nello stesso verso, poi i due lati b, sempre nello stesso verso. Con la prima operazione otteniamo un cilindro, con due bordi circolari; se piegandolo incolliamo i due bordi (pensate a un tubo di gomma), otteniamo proprio il nostro salvagente (Toro).
Questo nella pratica; ma noi dobbiamo trovare una relazione d'equivalenza che identifichi i lati b,b e i lati a,a.
Consideriamo la relazione sul quadrato in cui le equivalenze non banali sono
e
. Al solito, tutti i punti interni al quadrato sono equivalenti solo a se stessi.
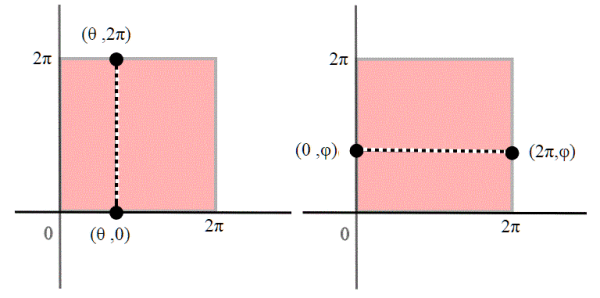
Il toro che abbiamo costruito in modo astratto, lo chiamiamo "toro topologico", ed è il quoziente del quadrato rispetto alla relazione di equivalenza sopra descritta. Ma è proprio il toro che conosciamo? Dobbiamo dimostrare che è omeomorfo al toro immerso nella spazio.
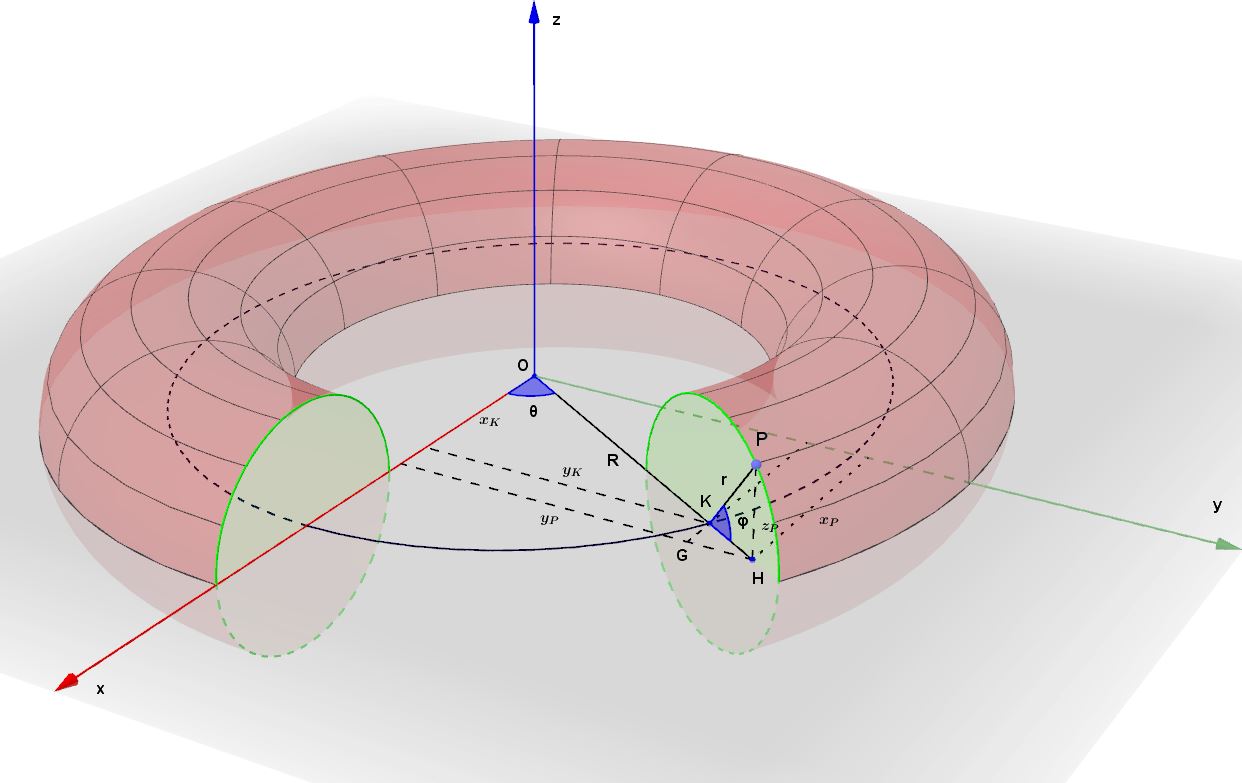
Ci serve perciò l'equazione parametrica del Toro nello spazio, e la recuperiamo direttamente sempre dall'articolo di Arturo, dove trovate anche la dimostrazione:
R>r
Per chi vuol approfondire ,senza cambiare pagina, inserisco qui sotto la dimostrazione di Arturo:
Equazione parametrica del toro
E' interessante determinare anche l'equazione parametrica del toro, ossia non in funzione delle coordinate cartesiane x,y,z di un suo punto, ma in funzione di due parametri geometrici che caratterizzano ciascun suo punto.
Facciamo riferimento alla seguente figura:
In essa ho evidenziato i due parametri caratteristici di ciascun punto situato su una superficie toroidale: l'angolo e l'angolo
. Per generare un toro, essi variano entrambi tra 0 e 360°. Esprimo, ora, le coordinate cartesiane del centro K della circonferenza generatrice passante per il generico punto P del toro in funzione di detti due parametri. Considero uno dei due triangoli rettangoli aventi ipotenusa OK ed applico i teoremi trigonometrici sui triangoli rettangoli:
Ora esprimo le coordinate cartesiane del punto P del toro in funzione dei parametri suddetti, constatando che il triangolo KGH è anch'esso rettangolo:
Essendo le suddette equazioni valide per ogni punto P del toro, generalizziamo indicando le sue coordinate con x,y,z. Otteniamo quindi:
Queste sono le equazioni parametriche del toro.
Costruiamo l'omemorfismo.
Chiamiamo f l'equazione parametrica appena vista.Quello che vogliamo dimostrare ora, è che esiste un omeomorfismo g:
dove Z è l'immagine di X tramite f (Z=f(X)). Verifichiamo la proprietà :
1 se ,
f(θ,0)=( (R+r)cosθ,(R+r)senθ,0),
f(θ,)=( (R+r)cosθ,(R+r)senθ,0)
per cui f(θ,0)=f(θ,)
2 se
f(0,φ)=((R+rcosφ),0,rsenφ)
f(,φ)=((R+rcosφ),0,rsenφ)
per cui f(0,φ)=f(,φ).
Quindi possiamo porre g([p])=f(p) essendo g ben definita, ovvero indipendente dal rappresentante della classe.
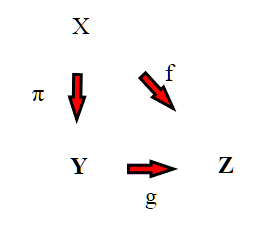
f è continua, quindi per la proprietà fondamentale del quoziente anche g è continua.
Torniamo adesso all'equazione parametrica di f. f non è iniettiva. Consideriamo un particolare del disegno tratto dallo studio della parametrica di Arturo.
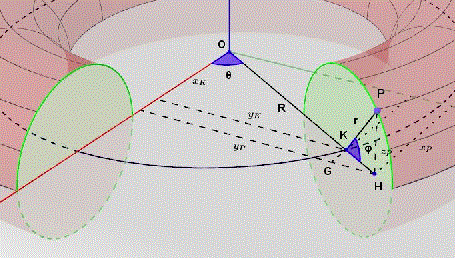
Abbiamo due parametri
che variano fra
. Sia
arbitrario ma fissato, ma interno all'intervallo, ossia
. In corrispondenza avremo una circonferenza di raggio r. I punti di tale circonferenza al variare di
fra
descrivono punti P della superficie del toro. Tali punti hanno valori univoci di
, ad eccezione del punto che si ottiene per
=0 in quanto tale punto si ottiene anche per
. Al variare di
, tali punti altro non sono che la saldatura che forma il cilindro, ed hanno coordinate
. Per
la circonferenza di raggio r viene a sovrapporsi con la circonferenza sempre di raggio r ma corrispondente a
. In questo caso, al variare di
tutti questi punti hanno la doppia rappresentazione
, Essi rappresentano la saldatura dei due bordi del cilindro. Notiamo allora che i punti dove la f non è iniettiva altro non sono che i punti delle equivalenze non banali descritte sopra.
g invece è iniettiva. Infatti g viene applicata alle classi di equivalenza di X. Se f viene applicata ad un punto interno del quadrato, f assume lo stesso valore solo in quel punto, che è equivalente solo a se stesso. Se invece applichiamo f ai punti dei segmenti che delimitano il quadrato, sappiamo che f assume lo stesso valore in e in
. f non è iniettiva in questi segmenti, ma sappiamo anche che i punti in essi sono equivalenti, quindi appartengono alla stessa classe. Essendo g([p])=f(p) questo significa che g è iniettiva.
Possiamo allora applicare il nostro teorema necessario:
Sia g : X -->Y un’applicazione continua e biunivoca. Se Y è compatto e Z è di Hausdorff allora g è un omeomorfismo.
g è continua e biunivoca. E' definita su Y che è un compatto, essendo immagine del compatto [0,] x [
] tramite
.
Z (il toro) è di Hausdorff, essendo un sottospazio di , immagine di X (f(X)). Quindi g è un omemomorfismo.
Il toro costruito con la topologia è quindi omeomorfo al toro immerso nello spazio, costruito in altro modo, ovvero come superficie di rotazione.
