Tutti sanno come lavora il GPS? Beh... penso proprio di sì dato che viene usato molto più delle bussole di una volta. Ma tutti sanno anche  che se la RR e la RG non fossero tenute in conto l’apparecchiatura non potrebbe funzionare?  Cercheremo di dimostrarlo con un esempio molto istruttivo che richiamerà (non fa mai male) il mix tra RR e RG che esiste e va tenuto in conto anche quando qualcosa si muove in un campo gravitazionale relativamente debole come quello della Terra.

Un modo molto semplice per togliere ogni dubbio, sarebbe quello di far cadere dall’alto la verità assoluta (stile mediatico odierno): “Usi il GPS?”, “Sì”, “Funziona?”, “Perfettamente!”, “Allora, visto che utilizza RR e la RG vuol dire che Einstein ha ragione e Galileo no. Punto e basta”.

Tuttavia, questo non è il nostro stile e cerchiamo, allora, di fare toccare le cose con mano direttamente a lui, al grande Galileo Galilei. Gli mostriamo il GPS e gli  spieghiamo come funziona lo strumento, semplificando enormemente la situazione...

Una configurazione ottimale

Siamo in P, in mezzo a un deserto, e vogliamo sapere la nostra posizione. Fortunatamente, esistono degli orologi ultra sincronizzati e precisi che inviano segnali da due punti lontani e che il nostro GPS sa raccogliere, registrando il tempo di arrivo contemporaneo dei due segnali (con un orologio altrettanto accurato). Il GPS sa anche la posizione di questi due orologi e sa anche l’istante di tempo in cui sono stati inviati i loro segnali (Fig. 1).

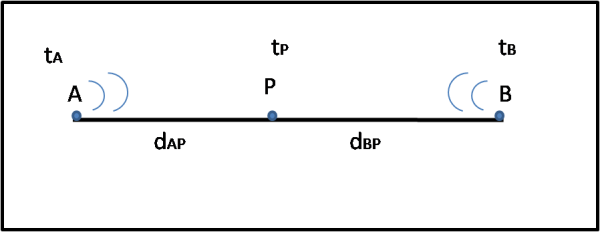
Beh… tutto è semplicissimo… basta conoscere la formula che lega velocità con tempo e spazio. Sia t_A il tempo di invio del segnale di A che arriva in P (codificato nel segnale) al tempo t_P. Sia invece t_B il tempo d’invio del segnale di B che arriva nello stesso istante t_P.

Basta scrivere le distanze tra A e P e tra B e P.

d_AP = c (t_P – t_A)

d_BP = c (t_P – t_B)

I secondi membri sono noti e quindi sono note anche le distanze tra A e P e B e P. In altre parole, P sa dove si trova e di conseguenza dove andare.

Entra in ballo Galileo

Galileo sorride e dice: "Attenzione! state facendo un grave errore. Io non so a che velocità viaggi la luce, ma sicuramente non potete scrivere le formule precedenti, in quanto non tengono conto del moto della Terra rispetto al Sole (chiamiamola v e immaginiamola pure costante e uguale a 30 km/s)." Poi, aggiunge: "Per accettare le vostre formule dovremmo imporre la velocità della luce costante in ogni sistema di riferimento... assurdo!"

Noi gli diciamo che, in realtà, le cose sono leggermente più complicate e che i due orologi che inviano i segnali A e B non si trovano sulla Terra ma su due satelliti artificiali, che assumiamo geostazionari su orbita equatoriale, così come assumiamo che il punto P stia sull’equatore terrestre esattamente sulla linea AB.  La Fig. 1 si trasforma nella Fig. 2.

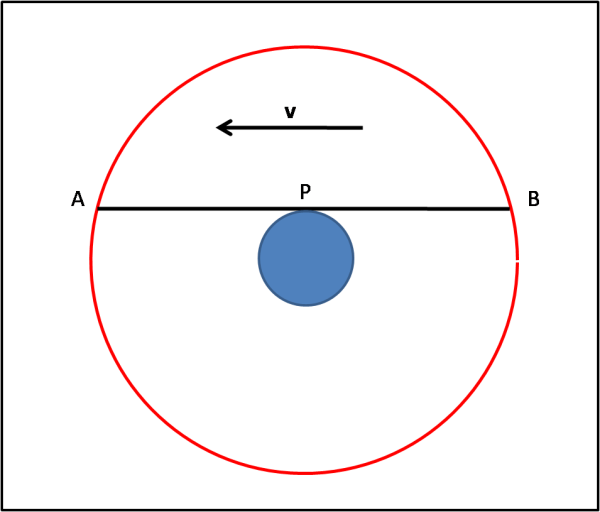
Galileo risponde: "Nessun problema, conosco molto bene il moto dei satelliti (modestamente ne ho appena trovati quattro attorno a Giove...) e comprendo perfettamente la configurazione che mi prospettate. Tuttavia, il discorso non cambia di una virgola dato che i satelliti si comportano come punti fissi nel sistema Terra e la seguono nel suo moto attorno al Sole.

Il genio pisano disegna rapidamente le Fig. 3  che si riferisce alla situazioni del trio APB a 12 ore di distanza.

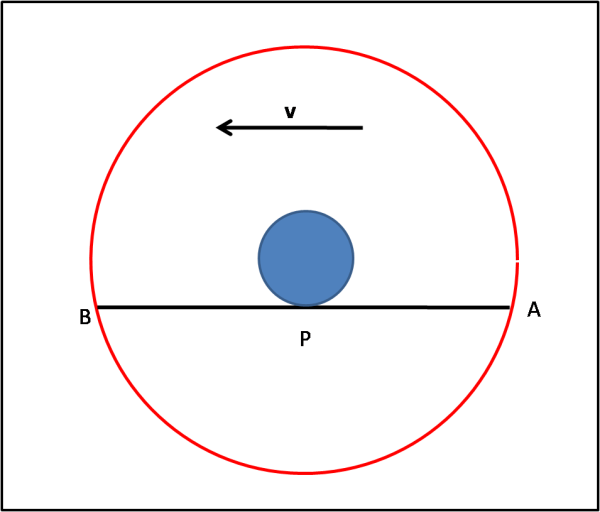
Galileo inizia con la Fig. 2. P riceve il segnale di A e legge il tempo di arrivo, che è lo stesso di quello partito da B. come già fattoci notare, la velocità con cui è arrivato il segnale di A  deve tener conto della velocità della Terra  v rispetto al Sole.  P non può che concludere che la velocità del segnale è data dalla SOMMA delle velocità della luce e della Terra. Ne segue che:

d_AP = (c + v)(t_P – t_A) = (c + v)Δt_A

Il segnale proveniente da B viaggia invece a una velocità decisamente minore (data dalla DIFFERENZA delle velocità):

d_BP = (c – v)(t_P – t_B) =  (c – v)Δt_B

Intanto la Terra gira e ci veniamo a trovare nelle condizioni di Fig. 3. I ruoli adesso si sono invertiti: E’ il segnale di B che viaggia più veloce, mentre quello di A rallenta. Galileo non è uno sprovveduto e già  capisce che se accettasse le regole del GPS (velocità costante) i risultati sarebbero alquanto diversi dai suoi: la posizione del punto P cambierebbe tra quanto calcolato in Fig. 2 e quanto calcolato in Fig. 3. Secondo lui, usando il GPS, la posizione di P sarebbe ballerina: il non potere sommare nessuna velocità a quella della luce comporterebbe una forte oscillazione della posizione di P nelle 24 ore.

Non gli resta che quantificare questo "spostamento" apparente che verrebbe rilevato dal GPS,  dato che lavora con una assunzione del tutto sbagliata (ossia c  = costante).  Ci propone, allora, di metterci in una posizione ancora più favorevole per la semplificazione del calcolo, ossia in un punto P che stia esattamente a metà strada tra due  A e B, in modo che d_AP = d_BP = d

Da quanto calcolato prima ottiene:

Δt_A = d/(c + v)           .... (1)

Δt_B = d/(c - v)            .... (2)

Sempre con lo stesso sorriso di prima ci dice che se avesse ragione il GPS la distanza d deriverebbe, invece, da una velocità costante, ossia varrebbero le relazioni:

d = c Δt_A  (calcolata rispetto ad A)

e

d = c Δt_B (calcolata rispetto a B)

Ma , ricordando la (1) e la (2),  può  scrivere:

d_AP = c Δt_A  = cd/(c + v) <  d_BP = c Δt_B = cd/(c - v)

La relazione non  lascia dubbi: le due distanze non  possono essere uguali.  In particolare quella tra B e P è maggiore di quella tra A e B

Il punto P non sta più nel mezzo di AB, ma più vicino ad A di una quantità pari a

s = (d_BP - d_AP)/2

Ossia:

s = (cd/(c - v) - cd/(c + v))/2 = (cd/2 )(1/(c – v) – 1/(c + v)) = cd (c+ v – c  + v)/(2(c² – v²))

s = cdv/( c² – v²)

Gli suggeriamo una rapida semplificazione che lui accetta senza fiatare. Anche se Galileo non conosce il valore della velocità della luce, ammette che, qualunque esso  sia, deve essere decisamente maggiore di v, per cui è d’accordo a trascurare il termine v² al denominatore. Ne segue:

s   ≈ dv/c

Galileo è molto fiero di sé e aggiunge che passando alla configurazione di Fig. 3 si otterrebbe lo stesso spostamento nel verso opposto. Ne risulta un’oscillazione non trascurabile.  Noi che conosciamo il valore di c possiamo stabilire l'enorme errore:

c = 300 000 km/s

v = 30 km/s

d = 40 000 km

da cui si ottiene si ottiene  s pari a circa 4 km!

Galileo ha ragione... no, ha torto...

Il guaio per il sommo pisano è che il nostro GPS non mostra assolutamente questa oscillazione e continua a dare sempre un valore esatto e costante di P. Galileo, che è uomo vero di Scienza, capisce subito che la costanza della velocità della luce è una realtà e che le sue formule sono quantomeno da rivedere. Sono proprio loro che danno luogo a una oscillazione della posizione!  Si rifugia in un angolo a riflettere sull’etere e su molte altre cose, anche se dovrebbe pensare al processo che ha in corso.

La faccenda,  così semplificata, dimostra già di per sé che la RR ha ragione, in quanto ottiene un ottimo risultato solo accettando uno dei postulati di Einstein: la velocità della luce è la stessa in ogni sistema di riferimento, da cui la si misuri. Introduce, però, quasi subito un altro problema che, se risolto, migliora di molto il risultato (Fig. 4).

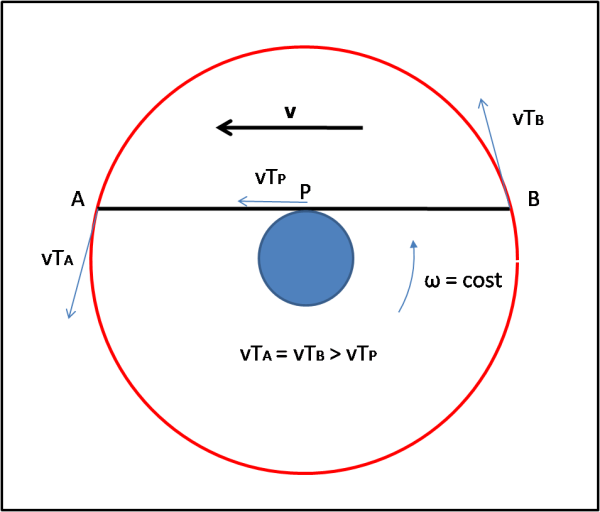
I satelliti, nel nostro esempio, ruotano con la stessa velocità angolare di P e quindi hanno una velocità tangenziale maggiore. Nel sistema di P, quindi, gli orologi di A e B sono visti rallentare e bisogna tenerne conto. Niente paura… il calcolo lo fa il GPS. E non si spaventa nemmeno se i satelliti non sono equatoriali, se hanno diverse altezze, se sono molti più di due e se P si trova in qualsiasi punto della Terra. Ma non basta ancora... si può essere ancora più precisi, conoscendo  le straordinaria precisione degli orologi atomici montati sui satelliti. Essi, infatti, sono più lontani dal centro di massa della Terra rispetto a P. Ciò vuol dire che entra in gioco anche la RG che ci dice che a diverse altezze corrisponde un diverso andamento del tempo…

In conclusione, non basta la RR, ma ci vuole anche la RG per ottenere una posizione  veramente accurata (perfino GAIA aveva dovuto tenerne conto)! Riguardo a questo mix tra RR e RG vorrei ricordare questo articolo, intorno alla Fig. 24.

Il GPS funziona davvero bene solo grazie al solito Albertino e, ancora una volta, non può che confermare in pieno le sue teorie. Nel frattempo, sembra che Galileo stia discutendo animatamente con un anziano signore dai lunghi capelli bianchi e dai grandi baffoni… Lasciamoli fare,  in fondo sono fatti della stessa pasta!

La morale

La relatività non complica la vita, ma la rende più semplice. Cosa c'è di meglio che considerare costante la velocità della luce invece di doverla sommare, sottrarre e molte altre cose? La verità è sempre la soluzione più semplice, siamo solo noi, quando non la capiamo, che la descriviamo con formule complesse e arzigogolate.

Ricordiamoci sempre che la massa non deforma solo lo spazio, come a volte si tende a spiegare in modo troppo semplificato (con disegni puramente geometrici), ma deforma lo spaziotempo. Il righello di Isalba (QUI, Fig,re 19 e 20),  si allunga e si accorcia in perfetto accordo con l'andamento del suo orologio!