Quiz cinematico bidimensionale: un cannone a doppio stadio **

09/08/19

Quiz cinematico bidimensionale: un cannone a doppio stadio **

Categorie: Fisica classica Tags: Scritto da: Vincenzo Zappalà Commenti:18

Ricaviamo l'equazione della traiettoria di un proiettile lanciato con un certo alzo e con una certa velocità iniziale e risolviamo un semplice problema di ... artiglieria.

Come avevo già preannunciato QUI, è piuttosto semplice ricavare l'equazione della traiettoria di un proiettile sparato da un cannone, conoscendo l'alzo  α (l'angolo tra la direzione iniziale del proiettile e la linea orizzontale) e la velocità iniziale uo.

In realtà, la prima parte del quiz serve anche a dimostrare che la traiettoria di un proiettile è una parabola (di solito si prende per buon questo fatto) e poi basta ragionare un poco. Darò una soluzione piuttosto lunga che permetta di ricavare diversi punti fondamentali della situazione. Si può risolvere, sicuramente, più velocemente. Ma i quiz devono servire anche e soprattutto per fare didattica...

Ciò che capita nel nostro quiz è che, appena giunto nel punto più alto della traiettoria, il nostro proiettile esplode e si separa in due frammenti di uguale massa. Il primo cade al suolo  in modo perfettamente verticale. Quale sarà la gittata finale del secondo frammento (ossia la distanza tra il cannone e il suo punto di caduta)?

Un utile espediente (proiettile a due stadi) o un tragico fallimento?

Ovviamente, vogliamo il risultato solo in funzione dei dati di partenza, ossia α e u0. Questo esercizio è del tutto personale e quindi prendetevela pure con me...

Vi giuro che poi la smetterò con i cannoni e cambieremo argomento... (forse)

 

 

Articoli correlati

18 commenti

  1. Arturo Lorenzo
    09/08/2019 at 16:13

    Vorrei essere certo di avere capito bene la situazione nel momento in cui il proiettile si trova nel punto di massima altezza e si separa in due frammenti. Poiché prima della separazione il proiettile aveva una velocità orizzontale uox (che in assenza di attriti resta costante) e dovendosi conservare la quantità di moto del sistema, perché uno dei due frammenti subito dopo l'esplosione cada verticalmente di botto, significa che l'esplosione del proiettile imprime al primo frammento una velocità orizzontale uguale ed opposta a quella che aveva prima dell'esplosione, tale cioè che, combinandosi vettorialmente con quest'ultima, la velocità orizzontale risultante sia nulla. Si tratta, quindi, effettivamente di una esplosione, che proietta le due parti del proiettile imprimendo loro una velocità aggiuntiva.

  2. Vincenzo Zappalà
    09/08/2019 at 16:26

    "...tale cioè che, combinandosi vettorialmente con quest'ultima, la velocità orizzontale risultante sia nulla..."

    non capisco bene cosa intendi dire... Il proiettile arriva con una certa velocità e una certa quantità di moto. Poi si rompe a causa di  una forza INTERNA al sistema. La quantità di moto deve restare la stessa che aveva prima dell'urto. Tutto qui... e non posso dire di più... :roll:

  3. Arturo Lorenzo
    09/08/2019 at 17:13

    Si, è come pensavo, volevo esserne certo, anche se trattandosi di "esplosione" e non di "rottura", era un dubbio tutto sommato superfluo.

    l proiettile esplode nel punto di massima altezza. Calcolo , dunque, prima le coordinate di tale punto, in un sistema di assi cartesiani con origine del punto di sparo. Dando per scontato che la traiettoria è una parabola, l'ascissa del suo punto di massima altezza, cioè del vertice V, è ovviamente pari a metà gittata. La gittata, una volta ricavata l'equazione della traiettoria, si ricava facilmente andando a cercare i punti di intersezione tra parabola e asse x. Alla fine ottengo, indicando con G la gittata, con uo il modulo della velocità di sparo e con \alpha l'angolo di sparo:

    G=\frac{2u_{o}^{2}}{g}sin\alpha cos\alpha

    Quindi, il punto di massima altezza del proiettile avrà ascissa G/2, rispetto all'origine sopra indicata, cioè:

    x(V)=\frac{u_{o}^{2}}{g}sin\alpha cos\alpha

    Ora mi serve l'ordinata di tale vertice, ossia la massima altezza raggiunta dal proiettile. Basta sostituire l'ascissa sopra ricavata nell'equazione della traiettoria per trovare dopo qualche passaggio:

    y(V)=\frac{u_{o}^{2}}{2g}sin^{2}\alpha

    A tale risultato si giunge anche per via ...fisica, considerando che lungo la direzione verticale , per la conservazione dell'energia meccanica, quella cinetica iniziale , pari a 1/2*m*uoy^2 si trasforma interamente in energia potenziale gravitazionale, pari a m*g*H, nel momento in cui il proiettile raggiunge la massima altezza, da cui, uguagliando le due quantità e sapendo che uoy=uo*sin\alpha:

    H=\frac{u_{o}^{2}}{2g}sin^{2}\alpha

    Ora vedo cosa succede al momento dell'esplosione. Un attimo prima la quantità di moto del proiettile intero è M*uox. Un attimo dopo, con i dati del problema, è m*ux , dove ho indicato con ux la velocità del secondo frammento. Il primo, infatti, cade verticalmente, quindi non incide sulla quantità di moto in direzione x. Quindi, essendo m=M/2 (ogni frammento ha massa uguale pari a metà di quella del proiettile intero) , uguagliando la quantità di moto prima e dopo l'esplosione ottengo:

    u_{x}=2u_{ox}

    Cioè, il secondo frammento subito dopo l'esplosione prende a muoversi con velocità orizzontale pari al doppio di quella che aveva prima dell'esplosione.

    Per inciso, perché il primo frammento dopo l'esplosione cada verticalmente, su esso l'esplosione imprimerà una velocità uguale ed opposta a uox , così che un attimo dopo l'esplosione esso risulta praticamente fermo lungo la direzione x (e inizierà a cadere verticalmente).

    Ora che so con quale velocità orizzontale il secondo frammento si muove subito dopo l'esplosione, e che , trovandosi nel punto di massima altezza ha velocità verticale nulla, posso allora considerare il suo moto dal punto di esplosione in poi come quello di un oggetto lanciato da una altezza H con velocità iniziale solo orizzontale di modulo pari a ux = 2 uox. Anche in questo caso la traiettoria seguita è un ramo di parabola e la distanza orizzontale coperta dal frammento si ricava facilmente dalla applicazione delle solite leggi del moto uniformemente accelerato in direzione y e uniforme in direzione x. A conti fatti, la distanza coperta lungo la direzione x dal punto dell'esplosione fino al suolo è  (uox = uo * cos\alpha  e  uoy = uo * sin\alpha) :

    \Delta s=\frac{2u_{o}^{2}}{g}sin\alpha cos\alpha

    Questa andrà a sommarsi alla distanza già coperta dal proiettile prima dell'esplosione, cioè metà della gittata G, quindi, in definitiva, la distanza tra l'origine e il punto in cui il secondo frammento tocca il suolo è G/2 +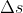 \Delta s cioè:

    G+\Delta s=\frac{3u_{o}^{2}}{g}sin\alpha cos\alpha

    (chiedo venia per eventuali strafalcioni, ma qui oggi il tasso di umidità è alle stelle e nel luogo dove sto usando il PC non c'è aria condizionata :oops: )

     

     

  4. Vincenzo Zappalà
    09/08/2019 at 17:26

    grazie Artù! Aspettiamo altre ... intrusioni...

  5. Francesco
    09/08/2019 at 20:14

    Scusate, c'è un modo per caricare foto dal cellulare, senza passare per siti vari. Sapete, sono vecchio stampo e ho bisogno di carta e penna: a pigiare sulla tastiera del telefono o mi si ingarbugliano le dita, o schiaccio troppi tasti.

     

  6. Vincenzo Zappalà
    10/08/2019 at 09:12

    chiedo aiuto agli esperti.... io sono negato e ho solo un vecchio cellulare che fa solo il... telefono!

  7. Umberto
    10/08/2019 at 09:21

    Sarò  telegrafico; le componenti orizzontali e verticali della velocità di sparo sono:

    V0x=U_{0}cos(\alpha )

    V0y=U_{0}sin(\alpha )

    Il tempo di  caduta dalla posizione di massima altezza si ottiene con la formula del moto U.A.:

    gt_{c}=V_{0y}, ossia

    t_{c}=\frac{V_{0y}}{g}

     

     

    al momento dello scoppio la velocità del proiettile è puramente orizzontale e vale U0x, di conseguenza la quantità di moto vale 2m*Uox, se m è la massa dei due frammenti . La forza che determina lo scoppio è interna al sistema del proiettile, pertanto vale il principio di conservazione della quantità di moto:

    2mU0x=v1*m+v2*m dove v1,v2 sono le velocità dei due frammenti (v1 è zero , quindi tutte e tre le velocità sono orizzontali dopo lo scoppi0). Essendo v1=0 (il primo frammento è in caduta libera dopo lo scoppio) deve  essere v2=2U0x. Quindi il proiettile percorre fino all'altezza massima con velocità orrizzontale U0x in un tempo Tc, poi conclude la parabola con velocità doppia. Pertanto essendo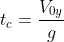 t_{c}=\frac{V_{0y}}{g} il tempo di caduta in entrambi i casi, la distanza orizzontale totale percorsa (la gittata) sarà:

    t_{c}U_{ox}+ t_{c}2U_{o}=\frac{V_{0y}}{g}\cdot V_{0x}+\frac{V_{0y}}{g}\cdot 2\cdot V_{0x}=\frac{3U_{0}^{2}sin\alpha \cdot cos\alpha }{g}

  8. Umberto
    10/08/2019 at 09:37

    scusate per alcuni errori di scrittura; nell'ultima formula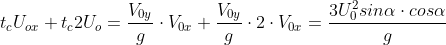 t_{c}U_{ox}+ t_{c}2U_{o}=\frac{V_{0y}}{g}\cdot V_{0x}+\frac{V_{0y}}{g}\cdot 2\cdot V_{0x}=\frac{3U_{0}^{2}sin\alpha \cdot cos\alpha }{g} al posto di Uo va V0x

    e più indietro, tipo in v2=2U0x, va sempre Vox e non Uox.

    Che pasticcio!

  10. Francesco
    10/08/2019 at 18:24

    Provo così

    Invece di graficare la traiettoria nel piano XY, ho tracciato le 3 leggi del moto nel piano tS,indicando:

    Sy(t) la parabola del moto uniformemente accelerato in direzione verticale y,

    Sx0(t) il moto rettilineo uniforme in x tra il lancio (t0=0) ed il momento di separazione dei due semiproiettili (t1, calcolato trovando il massimo della parabola Sy(t) tramite la sua derivata prima),

    Sx1(t)=costante il moto rettilineo uniforme lungo X del primo semiproiettile che casca verticalmente,

    Sx2(t) il moto rettilineo uniforme lungo X del secondo semiproiettile con velocità in direzione x pari a 2 volte la velocità iniziale in direzione x (da conservazione della quantità di moto).

     

     

  11. Francesco
    10/08/2019 at 18:26

    Purtroppo imgur non me lo carica. Peccato

  12. Francesco
    10/08/2019 at 19:10

    Foglio 1

    Foglio 2

     

  13. umberto
    10/08/2019 at 19:52

    perché non le carica? Ti dà errore?

  14. Francesco
    10/08/2019 at 20:06

    Credo che sia dovuto al fatto che accedo con il telefono e imgur non mi carica.

    Lo farei dal pc, ma è in ufficio. Ci penso la settimana prossima

  15. Vincenzo Zappalà
    11/08/2019 at 06:52

    dacci almeno il risultati finale, Francesco, in funzione di alfa e uo-

    Le figure sono più o meno intuibili facilmente...

  16. Francesco
    11/08/2019 at 10:30

    Ma il risultato della gittata è quello che hanno già indicato tutti

  17. Vincenzo Zappalà
    11/08/2019 at 10:55

    OK, Francesco, pensavo che non avessi letto gli altri risultati...

  18. Francesco
    13/08/2019 at 11:04

    Niente, non riesco a caricare nemmeno da pc (sito bloccato dai vari programmi di protezione e scambio dati).

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.