Categorie: Fisica classica Matematica
Tags: conservazione energia quantità di moto quiz urti ripetuti
Scritto da: Vincenzo Zappalà
Commenti:8
Urti ... numerici **
Un esperimento molto interessante che non è certo un vero quiz. Basta usare una fisica estremamente semplice. Tuttavia, per trovare quello che probabilmente non pensereste mai di trovare bisogna o fare tanti calcoli tutti uguali tra loro (poveri noi!) o farsi aiutare da qualche programmino predisposto allo scopo.
Prendete due masse (ad esempio a forma di cubo). La prima (m2) è sempre posta uguale a 1. La seconda (m1) è variabile e vale 100(d -1), con d numero intero positivo crescente. Mettete le due masse su un piano senza attrito con quella unitaria (m2) ferma e con quella variabile (m1) in moto da destra verso sinistra con velocità v posta anch'essa uguale a 1. Sulla sinistra della prima massa (m2) c'è una parete perfettamente elastica. Anche gli urti tra le due masse sono perfettamente elastici. Provate a contare il numero di collisioni che avvengono sia tra le due masse che contro la parete... Che cosa salterà fuori?
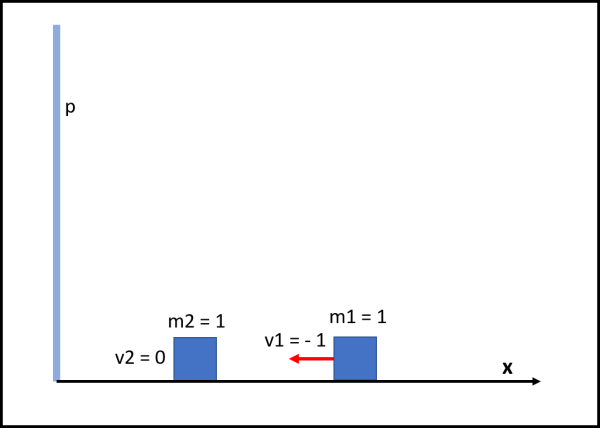
A titolo di esempio, provate a considerare il caso più semplice, ossia quello con d = 1. Si ha che le due masse sono entrambe unitarie, come indica la figura che segue:
Quante collisioni si ottengono?
Provate pure con d = 2 e divertitevi... anche se penso sia MOLTO utile farsi aiutare da qualche programma predisposto per ripetere una serie di azioni (la vera difficoltà sta solo nella ripetizione di un qualcosa di sempre uguale).
Trovato ciò che verrà fuori, bisognerà poi spiegare il perché... e qui le cose si complicano. Ne vedremo delle belle!






8 commenti
Nel caso "base" in cui le masse sono uguali direi che avvengano due urti tra le masse e un unico urto contro la parete.
La massa m1 si muove con velocità v1=-1 in direzione della massa m2 e dopo un tempo t1 la urta trasferendole completamente la propria quantità di moto: m1 si ferma e m2 parte a velocità v2=-1 in direzione della parete.
Dopo un tempo t2 la massa m2 urta la parete e rimbalza con velocità v2=1.
Dopo un tempo t3=t2 la massa m2 urta la massa m1 trasferendole completamente la propria quantità di moto: m2 si ferma e m1 parte a velocità v1=1 in direzione opposta alla parete, allontanandosi da m2 e cadendo dall'asse x dopo aver inciampato nella x e nella freccia.
Dopo pranzo penso agli altri casi, facendo eventualmente un programma di calcolo.
Il cibo fa bene !! Ho riattivato i neuroni fisici dormienti ...
Nel caso delle masse uguali è tutto facile. Ammetto di essermi basato molto sul "giochino" delle palline metalliche appese dove lanciando la prima rimbalza l'ultima, poi di nuovo la prima, ecc. ecc.
Nel caso di masse diverse la cosa è più complessa: per soddisfare sia il principio di conservazione della quantità di moto che quello di conservazione dell'energia le velocità delle masse dopo l'urto non possono semplicemente scambiarsi (con m1 = m2 invece si !), e nel caso specifico v1i = v2f e v1f = v2i = 0, ma per soddisfare ai due principi citati dovremo avere che, nel primo urto, m1 * v1i + 0 = m1 * v1f + m2 * v2f e 1/2 * m1 * v1i ^ 2 + 0 = 1/2 * m1 * v1f ^ 2 + 1/2 * m2 * v2f ^ 2 (le 'i' e le 'f' nelle velocità indicano iniziale e finale riferite al primo urto).
Benché io sia un informatico vorrei uscirne senza scrivere il famigerato programma di calcolo ...
Ragionando abbiamo che se il valore assoluto di v2f è minore del valore assoluto di v1f e v1f e v2f hanno segno opposto non c'è possibilità che la massa m2 dopo l'urto e dopo il rimbalzo contro la parete possa mai raggiungere la massa m1 per cui in questo caso avremo un urto tra le due masse e un urto contro la parete. Nel caso opposto prima o poi avverrà almeno un altro urto tra le masse, quando m2 raggiungerà nella sua fuga m1. Dopo quest'urto m1 aumenterà la sua velocità di fuga e m2 potrebbe tornare indietro o proseguire la fuga verso destra a velocità minore e in ambo i caso occorre ripetere il ragionamento.
Vorrei, quando avrò il tempo (non ora), cercare di dedurre matematicamente se mai m2 potrà uscire dal primo urto con una velocità in valore assoluto superiore a quella di m1 ... a dopo !
Cavolo, un altro numero magico (o meglio il numero magico x 10(d-1))
Ovviamente ho fatto un programmino veloce in mathcad che a d-1=7 mi impiega troppa memoria, ma credo che sia proprio quello.
Ora voglio capire perché: credo che sia da ragionare sulle intersezioni tra le due leggi di conservazione
Intendevo 10 elevato alla d-1
Scusate, gli smartphone sono abbastanza stupidi: non ha preso la formattazione corretta
Allora
Prima di tutto la descrizione del problema
Si tratta di urti elastici tra due masse m1 e m2 di velocità v1 e v2 e di urti tra m1 ed una parete di massa infinita.
Data l'assenza di attriti e il fatto che gli urti sono perfettamente elastici, prima e dopo l'urto tra le masse valgono la conservazione dell'energia cinetica (1/2*m1*v1i^2+1/2*m2*v2i^2=1/2*m1*v1f^2+1/2*m2*v2f^2, dove v1i, v2i, v1f, v2f sono le velocità iniziali di 1, di 2 e le velocità dopo l'urto di 1 e di 2), e la conservazione della quantità di moto (m1*v1i+m2*v2i=m1*v1f+m2*v2f).
L'urto di m2 con la parete non fa altro che cambiare il verso del moto di m2 (cioè v2f=-v2i).
Questo va ripetuto fino a quando la velocità finale di m2, maggiore di zero, è inferiore alla velocità finale di m1 maggiore di zero (in altre parole m2 viaggia verso destra a velocità inferiore a quella di m1, sempre verso destra).
Il programmino che ho scritto segue la seguente logica:
m2=1, m1=100^(d-1)*m2, v2i=0, v1i=-100^(d-1) (ho scelto la v1 grande per evitare che gli arrotondamenti dei decimali mi taglino qualche soluzione, ma concettualmente non cambia nulla se mettessi v1i=1).
Questo è prima del primo urto
Quindi urti=0
Primo urto
determino v1f e v2f dalla risoluzione del sistema di due equazioni (conservazione dell'energia e conservazione della quantità di moto) nelle due incognite v1f e v2f
Urto=Urto+1
Queste sono le condizioni prima del successivo urto, quindi v1i=v1f, v2i=v2f
Ora cominciano i SE
se v2i<0 ho l'urto con la parete, quindi
Urto=Urto+1 e v2f=-v2i
Re-inizializzo
v2i=v2f, v1i=resta quello di prima
SE invece v2i>0 e v1i<0 (cioè 2 verso destra e 1 verso sinistra) riapplico il sistema e calcolo le nuove v1f e v2f e Urto =Urto+1
Poi ripeto il ciclo fino a quando ho 0<v2i<v1i che mi interrompe i cicli.
Quindi viene:
m1=m2 Urti=3
m1=2m2 Urti=5 (non c'entra nulla, solo per verificare che il programma funzioni)
m1=3m2 Urti=5 (ancora, come sopra)
m1=10m2 Urti=10 (non c'entra nulla, solo per verificare che il programma funzioni)
m1=100m2 Urti=31 (intero di π *10)
m1=100^2*m2 Urti=314 (intero di π *10^2)
m1=100^3*m2 Urti=3141 (intero di π *10^3)
m1=100^4*m2 Urti=31415 (intero di π *10^4)
m1=100^5*m2 Urti=314159 (intero di π *10^5)
m1=100^6*m2 Urti=3141592 (intero di π *10^6)
m1=100^7*m2 Urti=31415926 (intero di π *10^7)
Poi mathcad richiede troppa memoria e si impalla
Comunque, se è sempre valido il teorema dell'ingegnere che dimostra che 60 è divisibile per 7 (essendo divisibile per 1, per 2, per 3, per 4, per 5 e per 6, non si vede per quale motivo non sia divisibile anche per 7), posso immaginare che il giochino continui anche oltre 7
Quindi abbiamo trovato un altro modo per calcolare π alla n cifra decimale contando il numero di urti e dividendoli per la radice quadrata del rapporto tra m1 e m2.
Per la spiegazione del motivo mi sono invece impantanato:
in un grafico con ascissa v1 ed ordinata v2, l'equazione della conservazione dell'energia cinetica (1/2*m1*v1^2+1/2*m2*v2^2=costante) è un'ellisse, mentre la conservazione della quantità di moto (m1*v1+m2*v2=costante) è una retta.
L'intersezione tra le due curve mi dà le due velocità v1 e v2 prima dell'urto e dopo l'urto.
Ora sto ragionando su come far venire fuori il numero di urti (e qui quasi ci sono) e poi legarlo con pigreco e qui mi impantano perchè devo legare un'ellisse con un angolo in modo da fa saltare fuori il pigreco (devo forse studiare i post che hai scritto su keplero, newton e feynman?)
caro Francesco,
che dirti... GRANDE! e non sei lontano dal perché... basta poco...