Categorie: Matematica
Tags: andamento disposizione più conveniente imballaggio quiz
Scritto da: Vincenzo Zappalà
Commenti:13
I gatti vogliono la sicurezza... ***
Avevo già preparato l'articolo di risposta al quiz dei gatti, ma siete troppo bravi! E allora, lo lascio a voi come ulteriore esercizio. Niente di veramente difficile, ma è necessario qualche calcoletto...
Si è visto che nella scatola dove stavano 40 gatti è possibile farcene stare 41. Tuttavia, i gatti hanno deciso di sapere a priori se sono stati inseriti al limite della capienza della scatola. E allora vi chiedo:
"Data una scatola di dimensioni a e b, con b≥a, come calcolare a priori il numero massimo di gatti che può essere contenuto in essa?" Vi accorgerete di un andamento particolare...
Buon imballaggio, anzi buon... ingattaggio!






13 commenti
beh ?! non risponde nessuno? Forza... è molto divertente!
Sicuramente meno di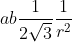 .....
.....
sempre ermetico... chiedevo qualcosa di più...
Un metodo per distribuire i nostri gatti-cerchi potrebbe essere quello fare una piastrellatura esagonale dello spazio rettangolare ed inscrivere i gatti-cerchi negli esagoni disponibili.
La piastrellatura è diversa a secondo di come sono orientati gli esagoni. Mi sono limitato a considerare i 2 possibili orientamenti con gli esagoni che hanno 2 lati paralleli o al lato più corto o al lato più lungo del rettangolo. Nelle due figure sotto c'è il risultato dell'ingattamento in un rettangolo con a= 9r e b=20r, dove r è il raggio del gatto-cerchio. Il numero di crechi sistemabili è diverso nei due casi.
All'interno dei cerchi ho indicato la coppia riga-colonna nella quale è stato sistemato il gatto.
Il numero di gatti sistemabili può essere trovato conoscendo il numero di righe e colonne.
Nella disposizione con 2 lati dell'esagono paralleli al lato corto del rettangolo, che nella figura ho chiamato disposizione A, il numero di righe (m) e colonne (n) è dato da queste due espressioni:
Nell'altra disposizione, che chiamo disposizione B, è data da queste altre due espressioni analoghe alle precedenti:
![m=intero\;inferiore\,di\left [ \frac{a}{r}-1 \right ]](http://latex.codecogs.com/gif.latex?m=intero\;inferiore\,di\left&space;[&space;\frac{a}{r}-1&space;\right&space;]) ed
ed ![n=intero\;inferiore\,di\left [ 1+\frac{1}{\sqrt{3}}\left(\frac{b}{r}-2\right ) \right ]](http://latex.codecogs.com/gif.latex?n=intero\;inferiore\,di\left&space;[&space;1+\frac{1}{\sqrt{3}}\left(\frac{b}{r}-2\right&space;)&space;\right&space;])
In entrambe le disposizioni il numero di gatti sistemabili è:
Non so se tra le due disposizioni ci sia sempre la disposizione con il maggior numero di gatti e se è prevedibile a priori quale delle due disposizioni è migliore.
In alcuni casi ci sono sfridi agli estremi che forse potrebbero essere utilizzati meglio se distribuiti tra i gatti. Ci devo pensare sopra ancora.
bene, bene... pensate...
Nel caso di asse di simmetria esagonale allineato coi lati a e b la soluzione è banale . Il problema sta nell'individuare le disposizioni coi lati disposti a un angolo inferiore a 60 rispetto alla simmetria dell'esagono.
Fatevi aiutare da Durer.
penso di capire cosa vuoi dire Leandro. Ma a noi basta valutare i due casi classici: a maglie quadrate ed esagonali regolari. Non esageriamo...
Mettiamola così: interessano solo le disposizioni regolari, sempre possibili... non casi peculiari.
cari amici,
temo di avere spiegato male la situazione che è più semplice di quanto stiate tentando di fare...
Come nel caso dei gatti, pensavo si capisse quali erano le due possibili sistemazioni da utilizzare. Ma mi ero spiegato male e quindi intervengo con una figura indicativa riguardo alle due configurazioni possibili che volevo fossero generalizzate con qualche formuletta:
Chiedo scusa...
Per non creare ulteriore caos, ho preferito inserire subito la soluzione che intendevo io e che si riferiva a quelle utilizzate per i 41 gatti. Se qualcuno vuole allargare il gioco, ha ovviamente campo libero...
Nelle configurazioni del tipo indicato in figura b, l'andamento dei gatti ospitati in funzione delle lunghezza a e b dovrebbero essere quello della figura seguente:
La figura mette in forma grafica le espressioni che ho scritto nel messaggio precedente per valori di b<14 e a<9
Dati a e b, il numero di righe m ed il numero di colonne n è:
Da queste si ricavano il numero di gatti ospitati:
ai due modelli della soluzione basterebbe aggiungere qualche modello in più e confrontare, tendendo magari al limite, ossia a b e a molto grandi... Io ho un paio di giorni incasinati e non so se riesco a contribuire