E' meglio che dia subito la soluzione che avevo in mente, ma che si riferiva solo alle due configurazioni legate ai nostri 41 gatti. Esse avevano entrambe la prima colonna in comune... Fabrizio e Leandro hanno allargato il problema e allora è meglio che crei una pausa. Se poi qualcuno volesse generalizzare ancora di più... sia il benvenuto.

Sistemati tutti e 41 i gattini dentro la scatola, vediamo di descrivere i semplici calcoli che devono essere fatti per conoscere "a priori" la sistemazione più conveniente. Una spiegazione estremamente utile per trasportare al meglio degli oggetti rotondi...

Il problema di fondo può essere descritto in poche parole: Dato un rettangolo con certe dimensioni b ≥ a, trovare il modo più conveniente per inserire al suo interno il maggior numero di cerchi di raggio unitario, basandosi sulle due configurazioni affrontate per fare posto al gatto rimasto fuori.  Si capisce subito che la problematica è molto importante per inscatolare oggetti circolari (o cilindrici) oltre che rappresentare un simpatico gioco geometrico.

Scegliamo due possibilità di inserimento dei cerchi (come abbiamo visto nel caso dei 41 gatti): o utilizzare un sistema a maglie quadrate o uno a maglie esagonali. La Fig. 1 mostra le due possibilità...

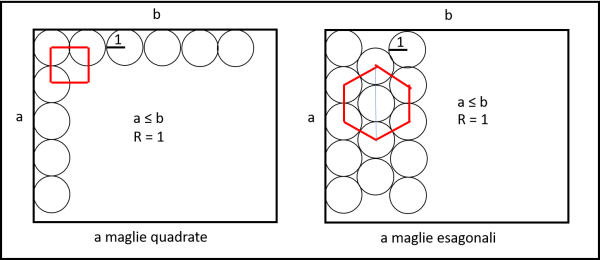
Nel caso dei gatti funziona meglio il secondo metodo, dato che ci permette di inserire anche il gatto numero 41. Tuttavia, vogliamo arrivare alla sistemazione ottimale nel caso più generale possibile.

E' sempre vero che conviene la distribuzione a maglie esagonali? Assolutamente no e tutto dipende, ovviamente, dalle dimensioni del rettangolo. Cerchiamo, perciò, di determinare a priori il metodo da usare, una volta fissati i lati a e b.

Quante righe e quante colonne

1. Maglie quadrate

E' il caso decisamente più facile. Si cominciano a inserire i cerchi a partire dall'angolo in alto a sinistra con i loro centri sempre allineati. Ci si deve fermare, ovviamente, quando sia in verso orizzontale che in senso verticale non ci sia più spazio per un altro cerchio. E', perciò, molto facile indicare il numero di cerchi che possono essere inseriti in funzione delle lunghezze a e b.

Quante colonne possono essere inserite? Presto detto: [b/2]. La doppia parentesi quadra sta a significare che prendiamo solo la parte intera del numero inserito. La divisione per 2 tiene conto che i cerchi hanno raggio  R uguale a 1 e, di conseguenza, ognuno di essi occupa uno spazio pari al diametro, uguale a 2.

Discorso analogo vale anche per le righe, il cui numero è [a/2].

Per sapere quanti cerchi possono essere contenuti del rettangolo basta pensare che sono possibili [b/2] colonne di [a/2] cerchi ciascuna. In conclusione abbiamo:

Numero di cerchi contenuti nella disposizione a maglia quadrata =

N_Q = [b/2] · [a/2] 

2. Maglie esagonali

Qui la faccenda è un po' più complicata. L'inizio è lo stesso di prima e la prima colonna rimane immutata. La seconda, invece, inizia più in basso, ma i cerchi riescono a inserirsi tra i cerchi della colonna precedente, guadagnando un po' di spazio. Quale sarà, allora, lo spazio a disposizione della seconda colonna? Per eccesso di chiarezza ingrandiamo la maglia esagonale nella Fig. 2 e soffermiamoci sul cerchio centrale e su due di quelli della colonna precedente. In rosso è stato marcato il lato sinistro dell'esagono di Fig. 1.

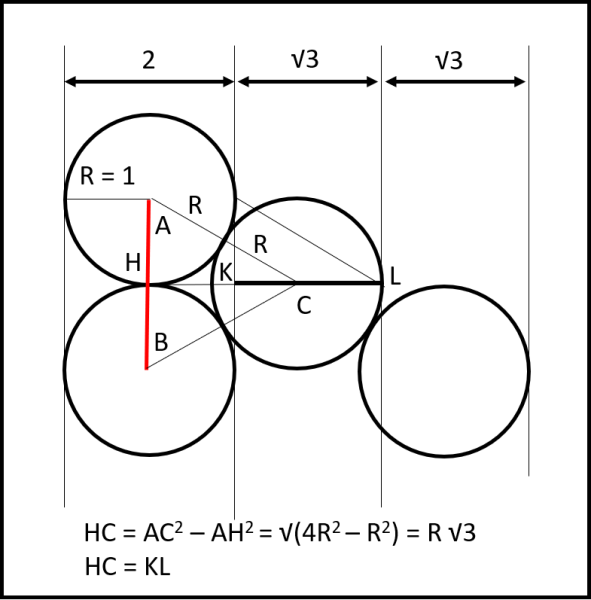
Applicando il teorema di Pitagora al triangolo AHC, che è metà del triangolo equilatero ABC, avente per lato il doppio del raggio, si ha:

HC = AC2 – AH2 = √(4R2 – R2) = R √3 = √3                  (ricordiamo che R = 1)

Ma

HC = KL      (basta spostare il triangolo verso destra di una lunghezza CL uguale al raggio R)

Ne segue che la seconda colonna (e anche la terza, la quarta, ecc,) occupa uno spazio pari a √3.

In numero di colonne diventa allora uguale a quante volte nel lato b riescono a stare il 2 (prima colonna) e √3 per tutte le altre. In parole matematiche:

Numero colonne della disposizione esagonale = 1 + [(b - 2)/√3]               .... (1)

A b abbiamo tolto 2 unità perché vengono occupate dalla prima colonna di cerchi. Poi dividiamo per √3 per sapere quante colonne possono stare di larghezza √3. Ovviamente, di questa divisione dobbiamo prendere solo la parte intera.

Passiamo, adesso, a considerare il numero di righe. I cerchi non hanno i centri allineati e quindi il calcolo è leggermente più complicato. Resta indubbio il fatto che la prima colonna contiene  lo stesso numero di cerchi del caso precedente (a maglia quadrata), ossia [a/2]. Il dubbio resta, però, sul numero di cerchi presenti nella seconda colonna (e poi nella quarte, nella sesta, ecc.). Per poter decidere dobbiamo calcolare la differenza tra la lunghezza a e la lunghezza occupata dai cerchi contenuti nella prima colonna. La lunghezza di un singolo cerchio è uguale a 2 e quindi la lunghezza totale occupata dai cerchi deve essere 2[a/2], dato che [a/2] è proprio il numero dei cerchi della prima colonna di diametro uguale a 2.

Consideriamo allora la differenza:

a - 2[a/2]

Abbiamo di fronte due possibilità (vedi Fig. 3):

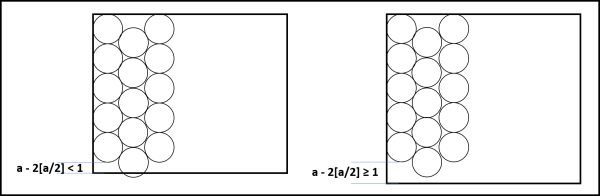
(I) a - 2[a/2] < 1

Siamo nella parte sinistra della Fig. 3. Lo spazio tra l'ultimo cerchio della prima colonna e il bordo inferiore del rettangolo è minore di 1, ossia minore del raggio R. In queste condizioni, l'ultimo cerchio della seconda colonna non può essere inserito e nella seconda colonna ci staranno, di conseguenza, solo [a/2] - 1 cerchi, ricordando che [a/2] è il numero di cerchi della prima colonna.

(II) a - 2[a/2] ≥ 1

Come si vede bene nella parte destra della Fig. 3, in questo caso il numero di cerchi risulta uguale a quello della prima colonna, ossia è uguale a [a/2]

Nel secondo caso si può già dare il risultato finale, ossia  il numero di cerchi contenuti nel rettangolo, ricordando la (1):

Numero di cerchi contenuti nella distribuzione a maglia esagonale con a - 2[a/2] ≥ 1 =

N_E+ = (1 + [(b - 2)/√3]) · [a/2]

Per comodità, chiamiamo n_b la quantità 1 + [(b - 2)/√3], trovata precedentemente, e che rappresenta il numero di colonne

N_E+= n_b · [a/2]

Nel caso (I) si deve  controllare ancora se il numero n_b è  pari o dispari.

Se n_b è pari, vuole dire che una metà delle colonne contengono [a/2] cerchi e l'altra metà [a/2] - 1, come riportato precedentemente all'inizio del caso (I). In termini matematici:

Numero di cerchi contenuti nella distribuzione a maglia esagonale con a - 2[a/2] < 1 e n_b pari =

N_Ep- = n_b/2 · ([a/2]) + n_b/2 · ([a/2] - 1)

Se n_b è dispari, vuol dire che le colonne che contengono [a/2] cerchi  sono una in più di quelle che contengono solo [a/2] - 1 cerchi. Traducendo anche questo risultato in termini matematici si ha:

Numero di cerchi contenuti nella distribuzione a maglia esagonale con a - 2[a/2] < 1 e n_b dispari =

N_Ed- = (n_b+ 1)/2 · ([a/2]) + (n_b - 1)/2 · ([a/2] - 1)

Riassumiamo quanto è stato trovato nella Tab. 1.

Diventa, adesso, molto semplice calcolare "a priori" quale sistemazione sia la più conveniente.

Applichiamo la Tab, 1 al caso dei nostri gattini (a = 10 e b = 16) e otteniamo proprio che la maglia quadrata porta a 40, mentre quella esagonale a 41 (Fig. 4).

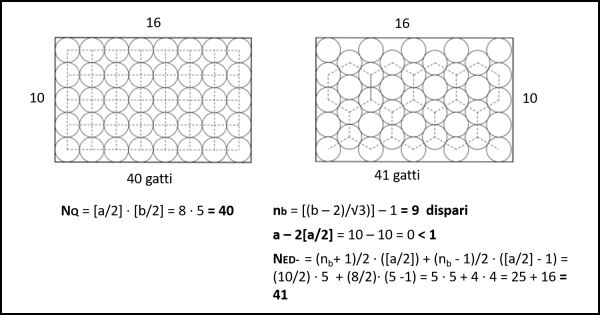
Aumentiamo i gatti e le dimensioni della scatola

Basterebbe fare un po' di prove e ci accorgeremmo che, all'aumentare delle dimensioni della scatola, la sistemazione esagonale tende a essere la più conveniente. Cerchiamo di capire perché... Per farlo usiamo una strategia leggermente diversa. Chiediamoci, innanzitutto: "Quali sono le dimensioni del più piccolo rettangolo che contenga h colonne di k cerchi (gatti) ciascuno di raggio unitario?".

Nel caso delle maglie quadrate il rettangolo ha dimensioni 2k · 2h.  Il rapporto tra l'area totale dei cerchi contenuti nel rettangolo e la sua area è:

A_C/ A_R = k h π/(2h · 2k) = π/4

Qualsiasi siano h e k il rapporto è costante.

Nel caso delle maglie esagonali il rettangolo ha dimensioni diverse, ossia ha il lato minore è pari a 2k + 1, mentre quello maggiore ha dimensioni pari a 2 + (h - 1)√3, come si vede in Fig. 5

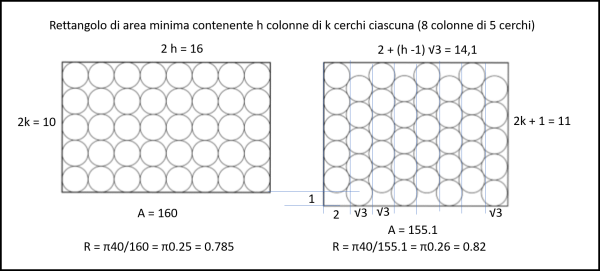
ossia :

A_C/ A_R= k h π/((2k + 1)(2 + (h - 1)√3))

Il rapporto è, in questo caso, funzione del numero di cerchi inseriti (h e k)

Studiamo ancora meglio questo risultato...

Nel primo caso il rapporto costante π/4 ci dice che questo rapporto è proprio uguale a quello esistente tra l'area di un cerchio e l'area del quadrato ad esso circoscritto. Nel secondo caso, invece, questo rapporto varia, ma per h e k sempre più grandi possiamo trascurare l'1, il 2 e il -1 del denominatore e, al limite, il rapporto tende  a:

A_C/ A_R = kh π/(2kh√3) = π/(2√3) 

Questo rapporto è quello esistente tra l'area di un cerchio e l'area dell'esagono ad esso circoscritto.  Questo rapporto è più grande di quello ottenuto a maglie quadrate e ciò significa che al crescere del numero di cerchi (e quindi delle dimensioni del rettangolo) la soluzione più conveniente è quella a maglie esagonali.

Vediamo in un grafico un caso particolare (facilmente generalizzabile) in cui poniamo h = 2k. In tale modo ogni area rettangolare può essere espressa in funzione della sola k. Nel caso delle maglie quadrate, il rapporto tra l'area totale dei cerchi e quella del rettangolo minimo che li contiene è, come detto, sempre costante ed è uguale a π/ 4 = 0.785. Nel caso delle maglie esagonali l'area del rettangolo è data da ((2k + 1)(2 + (2k - 1)√3))  ed è facile calcolare il rapporto tra l'area totale dei cerchi e lei, al variare di k. Il risultato ce lo mostra la Fig. 6.

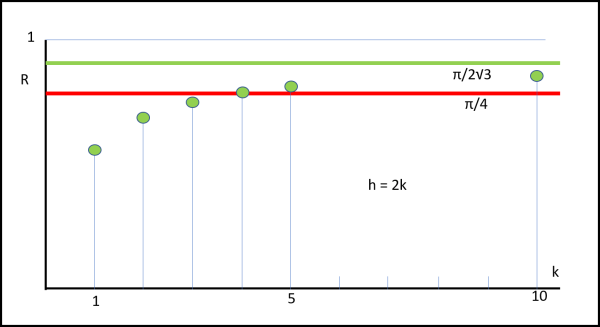
Per valori molto piccoli di k la soluzione più conveniente è quella a maglie quadrate, ma a partire da k = 5 è la soluzione a maglie esagonali che rende di più. Si vede bene come l'area totale dei cerchi tenda al valore di 0.91 che è quello corrispondente al rapporto tra cerchio ed esagono circoscritto.

Ci siamo divertiti con un po' di calcoli, ma adesso siamo sicuri di sapere scegliere a priori che scatola usare se dovessimo fare un ... trasloco.