Eccovi la mia soluzione (del quiz che trovate QUI) che vuole essere un esercizio di fisica (poca) e tanta matematica (in particolare trigonometria). Come già detto, si può probabilmente sveltire il procedimento, ma non è certamente sbagliato.

Prima strategia

Si può subito trovare il valore minimo della velocità del mostro per essere sicuri che Pippo si salvi. Basta che inizi a remare in direzione opposta al mostro in linea retta. Deve percorrere una distanza R a una velocità v. Affinché il mostro non lo raggiunga è sufficiente che la sua velocità gli permetta di percorrere un semicerchio di raggio R in più tempo rispetto al semi-attraversamento diretto di Pippo. Chiamiamo K il rapporto tra le velocità del mostro e di Pippo.

Il tempo che impiega Pippo è dato da:

t_P = R/v_P

Quello che impiega il mostro è dato da:

t_M = πR/v_M                     …. (1)

Perché perda il mostro, basta che sia:

t_M > t_P

πR/v_M > R/v_P

K = vM /vP < π

La salvezza è assicurata a patto che la velocità del mostro sia minore di π volte quella di Pippo. Vediamo la manovra in Fig. 1.

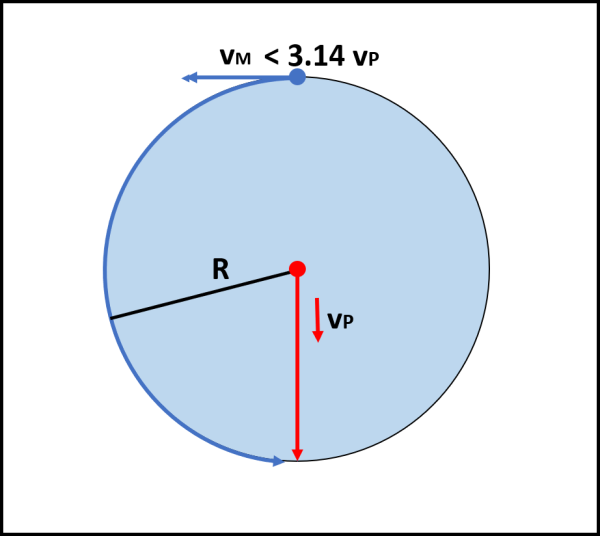
Questo caso, ovviamente ha poco interesse. Per cui supponiamo che K > π.

Seconda strategia

Ovviamente, la strategia più banale, descritta prima, non dà alcuna possibilità di salvezza a Pippo. In qualsiasi direzione lui tenti di dirigersi, il mostro arriverebbe sempre prima di lui. Di certo utilizzare linee curve non farebbe che peggiorare la situazione, dato che non farebbe  altro che allungare il tempo che Pippo impiegherebbe per raggiungere la sponda

Sembrerebbe, a questo punto, che Pippo sia destinato a finire tra i denti del mostro. Però, però… una strategia c’è!

Pippo oltre che ad andare in linea retta può anche descrivere dei cerchi nell’acqua, la cui velocità tangenziale in ogni punto sarebbe sempre uguale a v_P. Basta ricordarsi brevemente del moto circolare uniforme. Utilizziamo la Fig. 2.

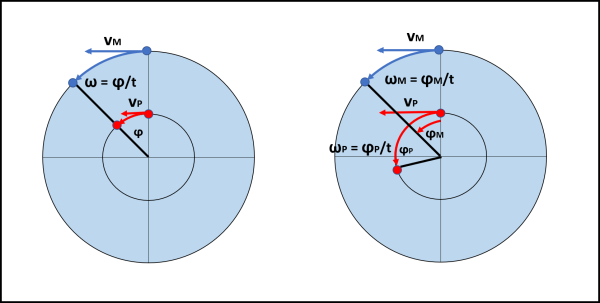
A sinistra abbiamo il mostro e Pippo che si muovono solidalmente su cerchi di raggio diverso. Se rimangono sempre allineati, vuol dire che la loro velocità angolare ω è uguale, ossia descrivono angoli uguali in tempi uguali. Ciò che conta per noi è invece la velocità tangenziale ossia quanta strada (o acqua) percorrono in tempi uguali. Nella parte sinistra è ovvio che per stare dietro al mostro (o viceversa) Pippo percorre un arco di cerchio nettamente minore. Il che vuol dire che la sua velocità tangenziale è minore di quella del mostro. In altre parole, basterebbe una velocità di Pippo anche solo leggermente più grande per far sì che Pippo guadagni in velocità angolare, come mostra la parte destra della figura. Addirittura in essa abbiamo posto le due velocità tangenziali uguali. Ci vuole ben poco affinché Pippo distanzi il Mostro fino a trovarsi a 180° da lui. Questo è però un caso estremo. Esiste però un cerchio che Pippo può percorrere, con una velocità tangenziale minore di quella del mostro, che gli permetta di guadagnare angolarmente rispetto al mostro. Questo cerchio dipende, ovviamente, dalla velocità del mostro.

Quantifichiamo meglio il problema…

Se Pippo iniziasse a remare lungo una circonferenza di raggio r_S attorno al centro del lago, come mostra la parte sinistra di Fig. 2, con la sua velocità ridotta manterrebbe la stessa velocità angolare del mostro.

ω_P = v_P/r_S

Quale sarebbe il raggio r_S tale da permettergli ancora di muoversi angolarmente come il mostro? Il che vuole anche dire che remando in cerchio al suo interno Pippo riuscirebbe a distanziare angolarmente il mostro.

Il mostro avrebbe sempre una velocità angolare pari a:

ω_M = ω_M/R

Affinché sia

ω_P > ω_M

deve essere

v_P/r_S > v_M/R

r_S < R/K

Restando all’interno di un cerchio di raggio r_S (che chiamiamo cerchio di salvezza) Pippo riuscirebbe ad assumere la posizione più favorevole rispetto al mostro, ossia quella che vede il terribile predatore in posizione opposta rispetto al centro del cerchio (Fig. 3). A Pippo basterebbe girare, spiraleggiando, per riuscire nel suo intento. Ma sarebbe più che sufficiente muoversi lungo una circonferenza di raggio R/2K per arrivare nel punto voluto.

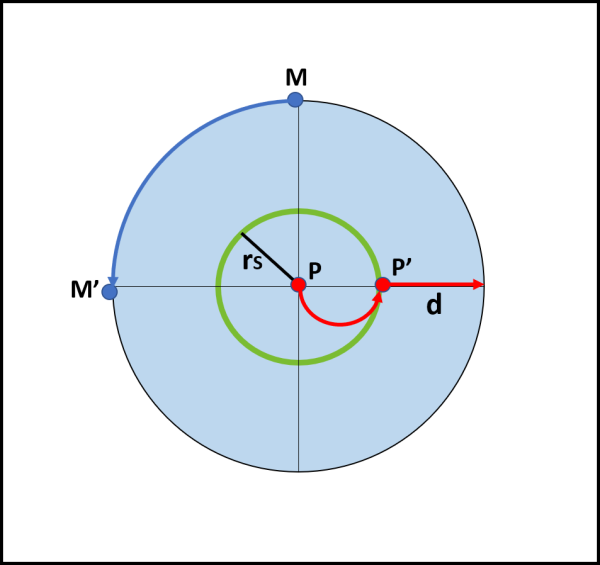
Raggiunta questa posizione, rimarrebbe a Pippo solo l’attraversamento di un tratto di lago d, che è dato da:

d = R - r_S

Per potersi salvare, Pippo deve riuscire a remare lungo d in un tempo minore del tempo che il mostro impiega a fare esattamente un semicerchio di raggio R.

Quanto tempo impiega Pippo a percorrere d?

d = R – R/K = R(1 – 1/K)

t_P = R(1 – 1/K)/v_P

quanto tempo impiega invece il mostro? Questo lo sappiamo già dalla (1)

t_M = πR/v_M

Pippo si salva se t_P < t_M

R(1 – 1/K)/v_P < πR/v_M

(1 – 1/K)/v_P < πR/v_M

(K – 1) K/K < π

K < 1 + π = 4.1416

Abbiamo trovato la velocità massima del mostro per permettere ancora a Pippo di salvarsi!

Ricapitoliamo la strategia:

Pippo si muove  lungo una circonferenza di raggio R/2K, come mostrato in Fig. 3. In tal modo Pippo percorre mezza circonferenza di raggio R/2K e il mostro solo un quarto di quella di raggio R. La posizione ottimale per la fuga rettilinea lungo d è raggiunta, a patto che sia K < 4.1416.

Bene, sembrerebbe di aver concluso… ma ne siamo proprio sicuri? Forse, forse… qualcosa si guadagnerebbe ancora se Pippo, arrivato nel punto esatto sul cerchio di salvezza, scegliesse un'altra traiettoria invece della d minore.

Terza strategia

E’ vero che Pippo allungherebbe il percorso, ma è altrettanto vero che lo stesso dovrebbe fare il mostro. Studiamo questa nuova possibilità. Escludiamo di battuta un cambiamento di direzione del mostro, dato che non sarebbe vantaggiosa per lui, perché nel frattempo Pippo avrebbe coperto un tratto più che sufficiente per scappare. Ne segue che una volta partito, il mostro non cambia direzione di corsa e Pippo decide immediatamente da che parte andare.

Consideriamo la Fig. 4...

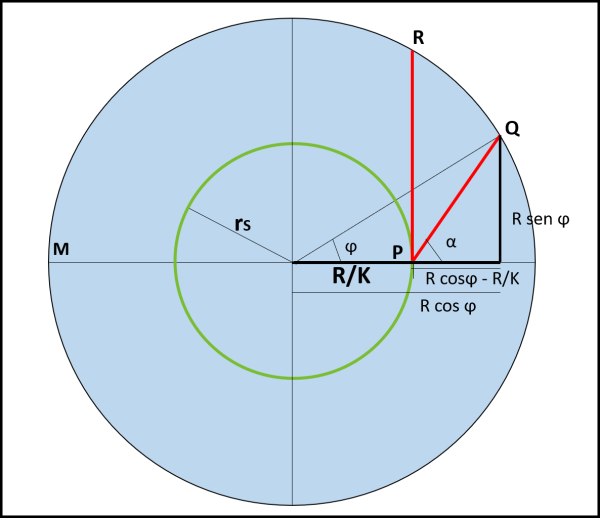
Come abbiamo visto in precedenza il raggio del cerchio di salvezza è pari a R/K. La nuova strategia inizia nel momento in cui Pippo riesce (e lo può sempre fare, come abbiamo dimostrato) a portarsi in posizione opposta al mostro rispetto al centro del lago. Consideriamo, adesso, un qualsiasi tragitto rettilineo d che vada da questo punto P alla sponda. Ovviamente, escludiamo il caso in cui d attraversi di nuovo il cerchio di salvezza, dato che, nel nuovo punto di contatto, Pippo si troverebbe in una posizione non ottimale con il mostro e dovrebbe nuovamente acquistare la posizione diametralmente opposta. Non può neanche andare in verso favorevole al mostro, dato che non farebbe che aiutarlo nella sua cattura. Ne segue che d può variare dal già studiato tratto orizzontale (di minore lunghezza) a quello tangente al cerchio di salvezza.

Chiamiamo φ l’angolo tra il tratto orizzontale e quello che potrebbe permettergli ancora di fuggire. Non è quindi la lunghezza di d che influisce sul risultato, quanto una relazione tra K e φ che permetta a Pippo di raggiungere la sponda in un punto Q in minor tempo di quello impiegato dal mostro per arrivare in quello stesso punto Q.

In parole matematiche

t_M > t_P

La distanza che deve percorrere il mostro è data da:

(π + φ)R                    .... (2)                (con gli angoli espressi in radianti)

Mentre quella che deve percorrere Pippo è d

Ne segue:

(π + φ)R/vM > d/vP

(π + φ)R/K  > d

Affidiamoci al caso limite, ponendo uguale al posto del simbolo minore

d = (π + φ)R/K        .... (3)

In questa relazione abbiamo tre incognite per cui dobbiamo cercare di eliminarne una (d) per ottenere la relazione tra K e φ.

Ma d può anche essere ricavato geometricamente dalla Fig. 4:

d² = R² sin² φ + (R cos φ – R/K)²

Dalla (3) si ottiene:

R² sin² φ + (R cos φ – R/K)² = (π + φ)² R²/K²

Che è la relazione cercata.

Scriviamola un po’ meglio, cercando di isolare K …

R² sin² φ + R² cos² φ + R²/K² – 2R² cos φ/K = (π + φ)² R²/K²

R² + R²/K² – 2R² cos φ/K = (π + φ)² R²/K²

1 + 1/K² – 2cos φ/K = (π + φ)²/K²

K² + 1 – 2K cos φ= (π + φ)²

K² – 2K cos φ + 1 - (π + φ)² = 0                  .... (4)

Risolvendola, si ottiene:

K = cos φ +/- √(cos²φ -1 + (π +φ)²)

O, ricordando che  sin²φ = 1 – cos²φ

K = cos φ +/- √((π + φ)² - sin²φ)

Prendendo la soluzione positiva (π + ϕ è sempre maggiore di sin φ) si ha:

K = cos φ + √((π + φ)² - sin²φ)              .... (5)

Non ci resta, adesso, che trovare il valore massimo di K in funzione dell’angolo φ. In tal modo conosceremo  la velocità che non deve superare il mostro per permettere la fuga di Pippo e, di conseguenza, quale traiettoria rettilinea d deve fare Pippo per ottenere tale condizione limite.

Un lavoro un po’ noioso, ma non certo difficile…

dK/dφ =  - sin φ + ( 2(π +φ) – 2 sin φ cos φ)/(2√((π +φ)² - sin²φ))) = - sinφ + ((π + φ) –  sin φ cos φ)/(√((π + φ)² - sin²φ))) = 0

sin φ √((π +φ)² - sin²φ)) = (π + φ) – sinφ cos φ

sin ²φ ((π + φ)² - sin²φ)) = (π + φ)² + sin²φ cos²φ - 2(π + φ) sin φ cos φ

(π + φ)² + sin²φ cos²φ - 2(π + φ) sinφ cos φ - sin ²φ ((π + φ)² - sin²φ)) = 0

(π +φ)² + sin²φ cos²φ - 2(π + φ) sin φ cos φ - sin ²φ (π + φ)² + sin⁴φ = 0

(π + φ)² (1 - sin ²φ) + sin²φ cos²φ - 2(π + φ) sin φ cos φ + sin⁴φ= 0

(π + φ)² cos²φ + sin²φ cos²φ - 2(π +φ) sin φ cos φ + sin⁴φ = 0

(π + φ)²/tan²φ+ cos²φ - 2(π + φ)/tan φ + sin²φ = 0

(π + φ)²/tan²φ - 2(π + φ)/tan φ + 1= 0

Ma questo è un quadrato perfetto !

((π + φ)/tan φ – 1)² = 0

(π + φ)/tan φ – 1 = 0

(π + φ)/tan φ= 1

(π + φ) = tan φ

Questa equazione non è semplice, ma si può risolvere sia graficamente (vedi Fig. 5) oppure per approssimazioni successive (metodo Newton-Rapshon) o con programmi già predisposti sul web.

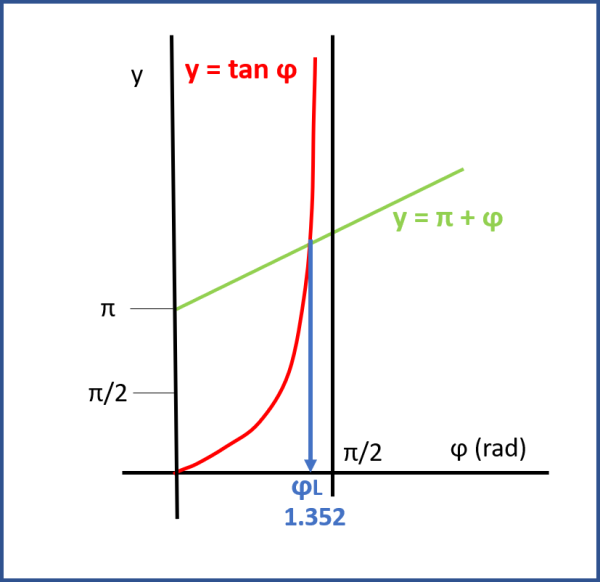
Il valore di φ capace di azzerare la derivata di K  è quindi:

φ= 1.3518 rad = 77.45°

Adesso bisogna inserire questo valore nell’espressione di K (5) e trovare il valore massimo della velocità del mostro

K = 4.6033

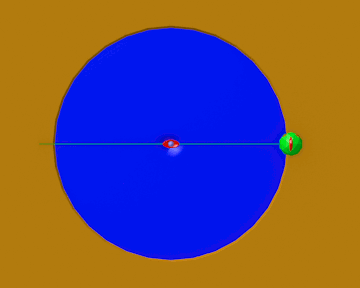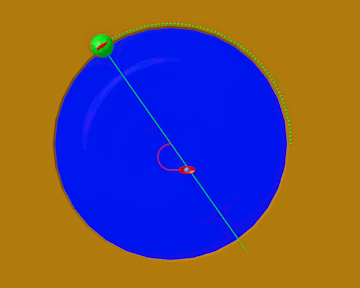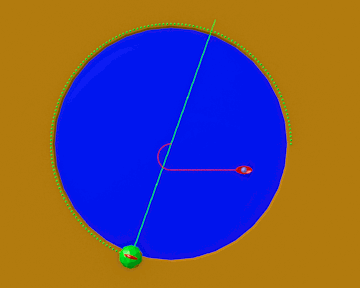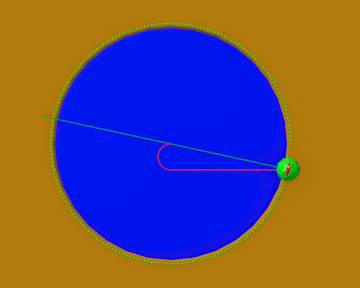
Il problema è risolto, ma sarebbe meglio calcolare l’angolo α, dato che è quello che deve seguire Pippo durante la sua traversata d. Usiamo sempre la Fig. 4.

d sin α = R sin φ

sin α = R sin φ/d

ma

d = (π + φ) R/K = sin φ R/(K cos φ)

sin α = R sin φ K cos φ/R sin φ

sin α = K cos φ

Nel caso della massima velocità del mostro ancora in grado di permettere la fuga, abbiamo

K cos φ = 4.6033 ∙ 0.2173 = 1.000

sin α = 1.000

ossia l’angolo α deve essere di 90°.

La Fig. 6, gentile regalo di Fabrizio, mostra l’intera strategia di Pippo per fuggire al mostro con la sua massima velocità.

Tutto bene quello che finisce bene, ma Pippo ha giurato di non andare più a pescare nel lago… anzi di non andare proprio più a pescare!

Il QUIZ lo trovate QUI

P.S.1: è facile che in tutti i passaggi abbia sbagliato qualcosa o ci sia una parentesi in meno o in più... se ve ne accorgete ditemelo subito!

P.S.2: Qualsiasi altra soluzione, non legata alla psicologia del mostro, è ben accetta!