Soluzione del quiz: UN QUADRILATERO SBILENCO E UNA SFERA **

16/02/20

Soluzione del quiz: UN QUADRILATERO SBILENCO E UNA SFERA **

Categorie: Matematica Tags: Scritto da: Umberto Cibien Commenti:0

Per chi non è a conoscenza, il quiz lo trovate QUI

Intanto grazie a tutti i partecipanti, e  invito a rileggere (se non lo avete già già fatto) le loro soluzioni  .

Quella da me proposta si basa sulle proprietà del baricentro. Si potrebbe scrivere in modo molto stringato, ma cerco di spiegarla in modo che anche in non esperti in certe proprietà vettoriali del baricentro possano comprenderla. La fisica qui non c'entra niente; lo stesso si avrebbe definendo una certa entità con operazioni da svolgere su vettori con moduli proporzionali a determinati numeri ( numeri detti anche scalari).

La prima cosa da osservare(e che era già stata detta nei commenti) è che ogni vertice del quadrilatero è equidistante dai due punti di tangenza alla sfera.

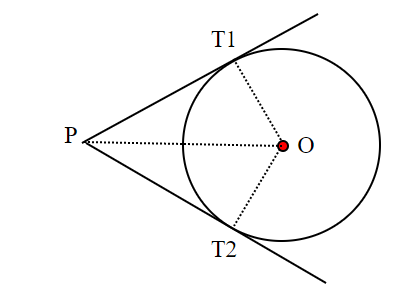
tangenti

abbiamo infatti a che fare con due triangoli rettangoli e isosceli (un lato è in comune, mente l'altro è il raggio. Quindi PT1=PT2.

Immaginiamo poi di "pesare" ogni vertice del quadrilatero con una massa proporzionale all'inverso della distanza dal punto di tangenza.  Si può scegliere un unica massa per ogni vertice appunto perchè le distanze dai due punti di tangenza sono le stesse.

Agendo in tal modo, il baricentro dei singoli lati viene viene a trovarsi  proprio nel punto di tangenza. Pensate per esempio ad un altalena con due ragazzi di peso diverso, appoggiata su un cuneo; affinchè stia in equilibrio bisogna proprio scegliere le masse in modo inversamente proporzionali alle distanze dei bordi dal cuneo. Ricordo poi altre due cose, di cui darò più sotto  una piccola dimostrazione .

  1. il baricentro di due punti è interno al segmento che li unisce. (pensate sempre all'altalena; le tavola nella situazione di equilibrio deve essere appoggiato al cuneo, questo è addirittura banale)
  2. Se abbiamo quattro punti, per calcolare il baricentro possiamo calcolare  il baricentro a due a due, poi calcolare il baricentro fra i due baricentri trovati. Questo è  forse meno intuitivo.

b

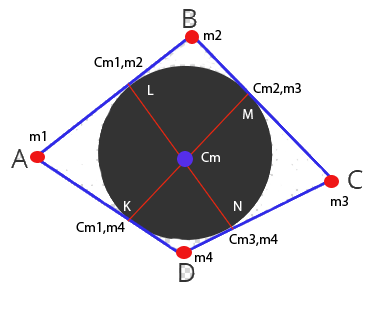
Ma allora il quiz è già risolto; consideriamo due punti opposti di tangenza, L ed N . L è il baricentro di   m1,m2 , mentre N è il baricentro di  m3,m4. Il baricentro di LN per la 1) deve trovarsi sul segmento che li unisce, ed inoltre per la 2) coincide con il baricentro di m1,m2,m3,m4. Consideriamo gli altri due punti  opposti, M,K; anche in questo caso il loro  baricentro  deve trovarsi sul segmento che li unisce, e coincide con il baricentro di m1,m2,m3,m4 per la 2). Ma allora , il baricentro totale del sistema m1,m2.m3,m4 deve trovarsi sull'intersezione fra i due segmenti, LN, MK. Ma questo vuol dire che i due segmenti si intersecano, quindi tutti e quattro i punti estremi dei segmenti si trovano nel piano definito da questi due. In parole  povere, dobbiamo individuare il baricentro del quadrilatero in due modi diversi per giungere alle nostre conclusioni.

Una piccola appendice; la definizione di baricentro e alcune proprietà che ne individuano la posizione.

Parliamo in modo strettamente  formale; il significato e le proprietà del baricentro   sono già state trattate in modo molto esaustivo dal Prof. Vincenzo in vari punti di questo sito. Basta cliccare sul tag   per trovarli.

Se ci troviamo nello spazio, per definire il baricentro abbiamo bisogno di un sistema di riferimento x,y,z. La formula che lo definisce in modo vettoriale è la seguente, se indichiamo con OG il vettore posizione del baricentro (O è l'origine degli assi):

OG=\frac{1}{M}\sum_{s=1}^{n}m_{s}OP_{s}

dove m_{s} sono le masse degli s punti, OPs il vettore che li individua nel riferimento di origine O, M la massa totale del sistema. Questa è una scrittura compatta; di solito si danno le tre coordinate, x_{g}=\frac{1}{M}\sum_{s=1}^{n}m_{s}x_{s} , y_{g}=\frac{1}{M}\sum_{s=1}^{n}m_{s}y_{s}, z_{g}=\frac{1}{M}\sum_{s=1}^{n}m_{s}z_{s}.

Il baricentro non dipende dal sistema di coordinate prescelto; per quanto riguarda la 1),

il baricentro di due punti è interno al segmento che li unisce , basta scegliere un sistema di riferimento in modo che, se A,B sono gli estremi del segmento, A coincida con l'origine, e B sia un punto sull'asse x preso sulla parte positiva. Essendo Yg=Zg=0, Xg ha solo la coordinata x diversa da zero, e inoltre più piccola di quella di A,  essendox_{G}=\frac{0\cdot m_{1}+x_{a}*m_{2}}{m_{1}+m_{2}}<x_{A}

Per quanto riguarda il punto 2), esso è valido chiaramente anche se i punti sono in numero qualsiasi. Quindi lo dimostriamo nel caso generale:

se un sistema di massa M è suddivisibile in due sottosistemi di masse rispettive: M1 e M2 e di baricentri G1 e G2 allora il baricentro del sistema complessivo è il baricentro dei baricentri dei due sottosistemi, cioè:

OG=\frac{M_{1}\cdot OG_{1}+M_{2}\cdot OG_{2}}{M_{1}+M_{2}}

se n sono i punti totali, spezziamo i due sistemi indicando con s=1,2,...p i punti del primo sistema, s=p+1,...,n i punti del secondo.

siano poi OG_{1}=\frac{1}{M_{1}}\sum_{s=1}^{p}m_{s}OP_{s} , OG_{2}=\frac{1}{M_{2}}\sum_{s=p+1}^{n}m_{s}OP_{s} i due baricentri. Allora:

\frac{M_{1}\cdot OG_{1}+M_{2}\cdot OG_{2}}{M_{1}+M_{2}}=\frac{1}{M}(\sum_{s=1}^{p}m_{s}OP_{s}+\sum_{s=p+1}^{p}m_{s}OP_{n})=\frac{1}{M}\sum_{s=1}^{n}m_{s}OP_{s}=OG\frac{M_{1}\cdot OG_{1}+M_{2}\cdot OG_{2}}{M_{1}+M_{2}}=\frac{1}{M}(\sum_{s=1}^{p}m_{s}OP_{s}+\sum_{s=p+1}^{p}m_{s}OP_{n})=\frac{1}{M}\sum_{s=1}^{n}m_{s}OP_{s}=OG

e siamo a posto.

 

Articoli correlati

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.