Questo articolo ci mostra come l'applicazione del teorema di Tolomeo (di cui abbiamo iniziato a parlare QUI) porta alla determinazione di due tra le più utilizzate formule di trigonometria.

Le formule che vogliamo ricavare sono quella relativa al seno della somma di due angoli e al teorema di Carnot o del coseno.

Il seno della somma

Ricordiamo la formula della somma del seno:

sen(α + β) = sen α cos β + cos α sen β

Consideriamo un quadrilatero qualsiasi iscritto in un cerchio tale che una sua diagonale coincida con un diametro, come mostrato in Fig. 2

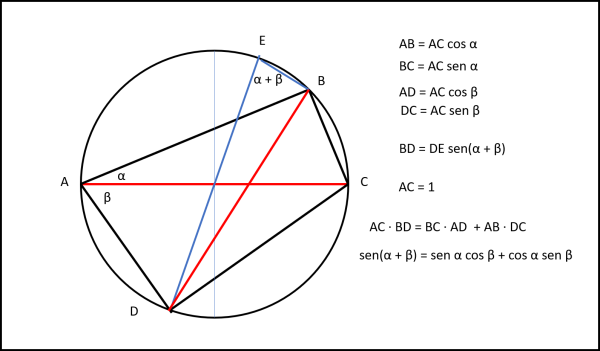
AC è un diametro del cerchio, per cui i due triangoli ABC e ADC sono entrambi rettangoli. Ne segue che:

AB = AC cos α

BC = AC sen α

AD = AC cos β

DC = AC sen β

Tracciamo il diametro DE

Il triangolo DBE è anch'esso rettangolo e ha anche un angolo pari ad (α + β) dato che è un angolo alla circonferenza dell'arco DB. Possiamo allora scrivere:

BD = DE sen(α + β)

Non ci resta che applicare il Teorema di Tolomeo al quadrilatero ABCD:

AC ∙ BD = BC ∙ AD  + AB ∙ DC

Ponendo AC = 1, otteniamo:

sen(α + β) = sen α cos β + cos α sen β

che è proprio la formula cercata e, dalla quale, si possono ricavare tutte le altre dello stesso tipo.

Si pensa che Tolomeo avesse già in testa i fondamenti della trigonometria.

Il Teorema di Carnot o del coseno

Disegniamo, in Fig. 3, un triangolo ABD qualsiasi e il cerchio ad esso circoscritto. Dal vertice B tracciamo la parallela ad AD fino a incontrare il cerchio in C. Il quadrilatero ABCD è un trapezio isoscele (potete dimostrarlo molto facilmente come esercizio).

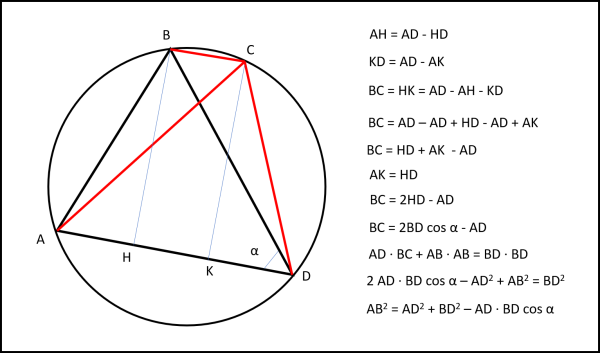
Essendo un trapezio isoscele i due lati non paralleli (AB e CD) , così come le due diagonali, sono uguali tra loro.

Ricaviamo il valore della base minore BC, trafficando un po' con i vari segmenti:

AH = AD - HD

KD = AD - AK

BC = HK = AD - AH - KD

BC = AD – AD + HD - AD + AK

BC = HD + AK  - AD

Ma

AK = HD

Per cui:

BC = 2HD - AD

Consideriamo il triangolo rettangolo BHD. Possiamo scrivere:

HD = BD cos α

Sostituendo:

BC = 2BD cos α - AD

A questo punto basta applicare il Teorema di Tolomeo al trapezio ABCD:

AD ∙ BC + AB ∙ AB = BD ∙ BD

e sostituire a BC il valore appena trovato:

2 AD ∙ BD cos α – AD² + AB² = BD²

AB² = AD² + BD² – AD ∙ BD cos α  

Che è proprio il teorema di Carnot applicato al triangolo ABD.

Notiamo come questo teorema non si altro che l'estensione del Teorema di Pitagora a un triangolo qualsiasi... se α  fosse retto, otterremmo proprio il celebre Teorema dato che il suo coseno diventerebbe zero.

 

QUI tutti gli articoli dedicati al Teorema di Tolomeo