La geometria, anche quella più semplice, può diventare un vero spettacolo. Soprattutto se c'è di mezzo Tolomeo, grandissimo scienziato, troppo spesso associato solo alla sua visione geocentrica dell'Universo.

Spesso e volentieri si associa Tolomeo alla sua visione dell'Universo, in cui la Terra stava decisamente al centro e i pianeti eseguivano strani balletti per  riuscire a confermare le osservazioni. Sappiamo anche quanto la visione tolemaica abbia rappresentato per secoli e secoli un dogma assoluto per la chiesa e come sia stato utilizzato per reprimere ogni tentativo di crescita culturale fino ad arrivare ai casi eclatanti e celebri di Giordano Bruno e di Galileo Galilei. Ciò che era una visione essenzialmente geometrica è stata trasformata in una verità assoluta con conseguenti atti criminali e nefasti nella storia del medioevo e anche oltre. Guai a pensare e a proporre visioni alternative, troppo logiche e indipendenti e, quindi, avanti con le stragi degli eretici, con l'inquisizione e, addirittura, con l'odierna riabilitazione molto parziale del genio galileiano e il continuo rifiuto di pentimento nei confronti di Giordano Bruno.

Oggi, a causa delle ricadute religiose ed etiche sopra descritte, lo stesso Tolomeo è diventato quasi uno dei "cattivi" dei film western, sconfitto finalmente dai "buoni" Copernico e Galileo.

Eppure Tolomeo è stato uno dei massimi  scienziati dell'antichità, non è certo colpa sua se il suo metodo, sicuramente geniale anche se errato, era più che sufficiente per confermare le osservazioni di quei tempi e per essere preso come verità assoluta e non modificabile da una chiesa per aveva interessi non certo scientifici... (tra parentesi, non ci ricorda un po' la verità attuale sul Global Warming?). I suoi contributi eccezionali vanno dalla stessa astronomia alla geografia, dall'ottica alla geometria. Ecco, proprio sulla geometria vorrei ampliare il discorso e mettere in evidenza un teorema che già abbiamo imparato a conoscere (e a dimostrare) ma che è spesso poco conosciuto, malgrado abbia in sé  le radici per risultati conosciuti oggi con altri nomi nel campo della trigonometria e non solo.

In poche parole, vorrei trattenermi per varie puntate sul Teorema di Tolomeo e sulle sue ricadute. Un teorema di una generalità enorme che sarebbe giusto ottenesse il  giusto riconoscimento nelle scuole. Per iniziare, un bellissimo e ghiotto antipasto: nientepopodimeno che il teorema di Pitagora! Quest'ultimo è forse il più conosciuto tra i teoremi di geometria, ma ben pochi sanno (forse) che è solo e soltanto un caso particolare del Teorema di Tolomeo. Esso deriva, infatti, molto banalmente da una sua semplificazione. Cominciamo con questo, allora, e poi ci dedicheremo a due celebri teoremi trigonometrici.

Infine, per chi ama i giochi di prestigio della geometria, cercheremo di dimostrarlo in un modo veramente geniale (non l'ho certo ideato io), estendendo una relazione che ha quasi del ridicolo:

dato un segmento AB di una retta e preso un punto intermedio C, possiamo concludere che AC + CB = AB

Non ci crederete, ma questo diventa proprio l'enunciato del teorema di Tolomeo. Non sarà cosa immediata, ma lo descriveremo con molta calma e accuratezza, imparando molti altri giochi geometrici. Chi ha detto che non ci si può divertire con la matematica e la geometria anche di livello elementare?

Bando alle ciance, ricordiamo l'enunciato più classico del Teorema di Tolomeo.

Dati quattro punti qualsiasi su una circonferenza si ottiene, ovviamente, un quadrilatero. Bene, Tolomeo dice che:

La somma dei prodotti dei lati opposti del quadrilatero è uguale al prodotto delle sue diagonali

Considerando la Fig. 1 (a sinistra), possiamo subito scriverlo in termini matematici:

AD ⋅ BC + AB · CD = AC · BD

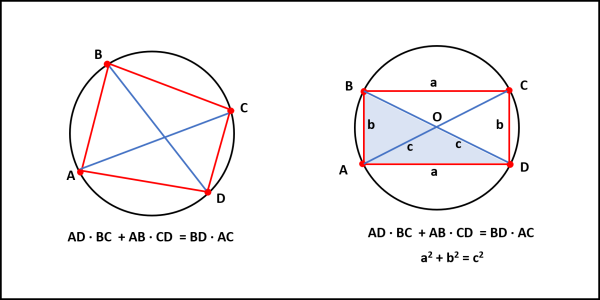
Proviamo a prendere un quadrilatero molto speciale: un rettangolo. Esso è sicuramente inscrivibile in un cerchio dato che le sue diagonali si incontrano nel suo centro e ne rappresentano due diametri (Fig. 1, a destra). Inoltre, in un rettangolo i lati opposti sono uguali. Chiamiamoli a e b , mentre chiamiamo c le diagonali. Applichiamo il teorema di Tolomeo e otteniamo:

a · a + b · b = c · c

a² + b² = c²

Che non è altro che il teorema di Pitagora dato che gli angoli del rettangolo sono tutti e quattro retti.

Fantastico no? Pitagora deriva da un caso particolare del Teorema di Tolomeo. E siamo solo all'inizio...

QUI tutti gli articoli dedicati al Teorema di Tolomeo