Questo articolo, oltre a dare la soluzione più rapida al problema posto qualche giorno fa, ci mette di fronte a una divertente soluzione seguita da un paio di matematici cinesi che sono riusciti a scalare l'Everest per andare da un villaggio a un altro, uniti da una breve e comoda superstrada... In altre parole: come complicare le cose semplici... Non perdetevelo!

Fabrizio ha risolto il quiz in modo brillante e ben diversamente dai cinesi di cui parlavo. In realtà, si può ottenere lo stesso risultato ancora più rapidamente se si ricordano due teoremi legati alle corde di un cerchio.

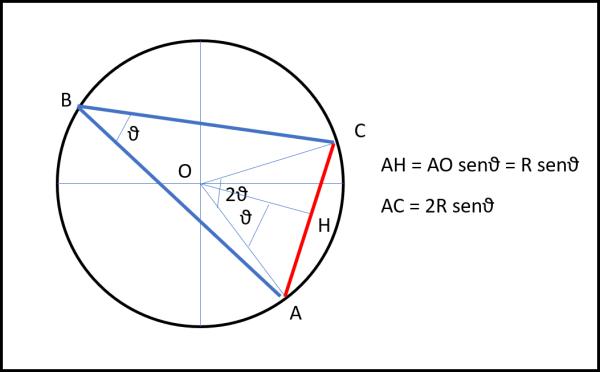
Il primo (teorema trigonometrico della corda) è veramente banale, ricordando che l'angolo al centro di un arco di circonferenza è uguale al doppio dell'angolo alla circonferenza dello stesso arco. Basta considerare la Fig. 1 e si ha subito la lunghezza della corda in funzione del raggio R e dell'angolo alla circonferenza θ.

Il triangolo OAC è ovviamente isoscele e si può scrivere immediatamente che

AH = AO sen θ = R sen θ

ossia

AC = 2R sen θ

Qualcuno potrebbe subito dire: "Molto bello, ma noi non conosciamo il raggio del cerchio R...". Nessun problema, il raggio fa la sua comparsa, ma sparisce velocemente...

Passiamo al secondo teorema, quello sicuramente meno conosciuto anche se molto, molto antico e che, come tale, non fa uso di trigonometria. Esso prende nome di Teorema di Tolomeo e si riferisce a un qualsiasi quadrilatero inscrivibile in un cerchio. Disegniamo la Fig. 2.

Il teorema dice che la somma dei prodotti dei lati opposti è uguale al prodotto delle diagonali. Possiamo anche dimostrarlo abbastanza facilmente (se lo ha fatto Tolomeo...), ma prima risolviamo il nostro "quiz".

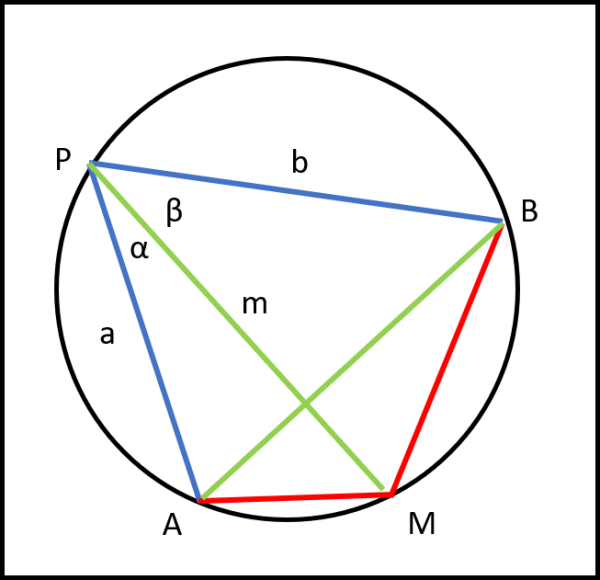
La Fig. 2 non è altro che la Fig 4  dell'articolo precedente e applichiamole i due teoremi.

Dal primo abbiamo subito:

AM = 2R sen α

MB = 2R sen β

AB = 2R sen(α + β)

Dal secondo:

PM ∙ AB = AM ∙ PB + PA ∙ MB

2R m sen(α+ β) = 2Rb sen α + 2Ra sen β

Come già accennato, 2R può tranquillamente essere eliminato e si ottiene:

m  sen(α+ β) = b sen α + a sen β

e, infine:

m  = (b sen α + a sen β)/sen(α+ β)

Ovviamente, questa formula generale può essere utilizzata anche per il caso α = β = θ, trattato nell'articolo precedente:

m = (b sen θ + a sen θ)/sen 2θ = (a + b) senθ/sen 2θ = (a + b) senθ/(2 senθ cosθ) = (a + b)/(2 cos θ)

dove abbiamo usato la formula trigonometrica dell'addizione degli archi:

sen 2θ = sen (θ + θ) = sen θ cos θ + cos θ sen θ = 2 sen θ cos θ.

Dimostrazione del teorema di Tolomeo

Consideriamo la Fig. 3. 

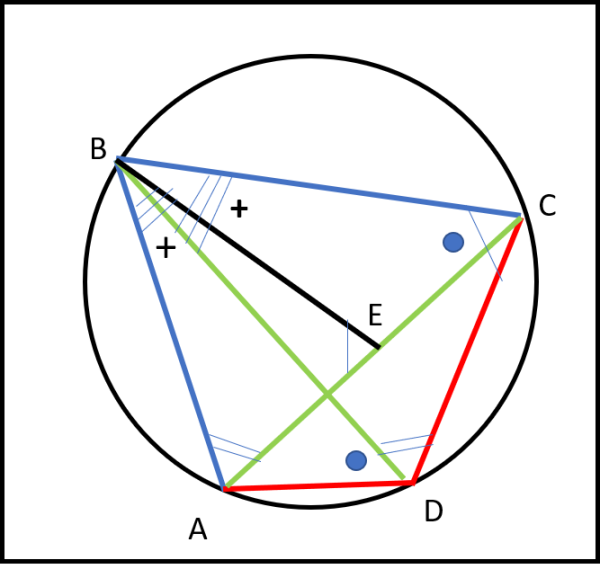
Lungo la diagonale AC identifichiamo il punto E tale che l'angolo AEB sia uguale all'angolo DCB. Ne segue che i triangoli BAE e BDC sono simili. Infatti, l'angolo in E e quello in C sono uguali per costruzione, mentre quello in A e quello in D sono uguali in quanto angoli alla circonferenza dello stesso arco BC. Possiamo perciò scrivere:

AE/CD = AB/BD

o, ancora:

CD · AB = AE · BD             .... (1)

I triangoli ABD e EBC sono anch'essi simili in quanto gli angoli in B sono uguali. Infatti:

ABE = DBC  (dalla similitudine dei triangoli BAE e BDC)

ABE - DBE = DBC - DBE (abbiamo sottratto lo stesso angolo sia a sinistra che a destra)

ABD = EBC

Gli angoli in D e in C sono uguali in quanto angoli alla circonferenza dello stesso arco BA. 

Ne segue, allora, che:

EC/BC = AD/BD

o, ancora:

BC · AD = EC · BD              .... (2)

Sommando la (1) e la (2)

CD · AB  + BC · AD = AE · BD  + EC · BD    

CD · AB  + BC · AD = (AE + EC) · BD = AC · BD

C.D.D.

Finalmente, risolto il problema (restiamo sempre in attesa di qualche commento da parte degli amanti della musica...), veniamo alla parte più divertente. Io reputo il popolo cinese tra quelli con maggiore cultura alle spalle e capaci di qualsiasi scoperta, ma, a volte, riescono a complicare le cose semplici. Questo è proprio il caso ...

Il video che segue, tra qualche carattere cinese e qualche carattere latino, riesce a trovare la formula finale, ben più complicata della nostra... e con tanta fatica trigonometrica (quasi venti minuti di formule)!

Un altro cinese, però, si accorge che la formula potrebbe essere compattata e dà luogo a una bellissima sfilata di formule trigonometriche (circa 10 minuti) che, alla fine, portano alla nostra soluzione.

E pensare che bastava conoscere Tolomeo...

P.S.: la soluzione del caso più semplice (corda bisettrice) l'avevo recuperata da un altro video, anch'esso, però, ignaro del teorema di Tolomeo.

Commento finale (per Frank soprattutto): questo è un caso semplice, ma indicativo che dimostra come, per risolvere problemi odierni e molto utili in campi anche diversi della scienza, è sempre molto importante conoscere molto bene i lavori degli antichi (anche se avevano una visione non proprio esatta del Sistema Solare...). Filosofia della Scienza ?

Il quiz lo trovate QUI