In questo articolo vedremo come trasportare concetti applicati ai vettori ordinari di R^n , quali  norma (lunghezza) prodotto scalare, trasformazioni lineari, matrici , scomposizioni tramite una base, le proiezioni su tale base (e un concetto nuovo, che vedremo in seguito, gli autovalori e non  dimentichiamoci di Pitagora!)  ad uno spazio in cui i vettori non sono proprio vettori ma altresì funzioni, e il loro prodotto scalare definito tramite un integrale, ossia in modo molto diverso da quello usuale che noi conosciamo. Arriveremo poi ad una interessante applicazione di questi spazi (detti di Hilbert) alla fisica. Chi ha studiato elettronica , come qualcuno in questo sito, immagina già  dove andremo a parare. Ma non solo, anche in un settore molto "prezioso" della fisica teorica.

Sfruttando un po' dei concetti, formali e non formali, esposti negli ultimi articoli della sfera di Poincarè, in particolare quelli sugli spazi metrici e sui prodotti scalari, siamo (forse) in grado di affrontare un argomento di fondamentale importanza non solo in matematica, ma anche nella fisica " moderna ". Riporto qui la parte iniziale dell'articolo che trovate qui, e in cui sono espressi dei concetti e delle definizioni di importanza fondamentale per gli spazi di Hilbert, che d'ora in poi denoteremo con la sigla S.H. Non è necessario rileggere l'articolo, riporto qui il materiale che serve.

Le metriche negli spazi vettoriali, topologici e nelle varietà.

Cos'è una metrica? Lo abbiamo visto in modo molto generale qui, dove ci si riferiva ad un insieme qualsiasi. Ma in questo contesto, quello degli spazi vettoriali,possiamo parlare di coordinate. Infatti, dove abbiamo a che fare con delle coordinate possiamo definire una distanza partendo da un prodotto scalare (funzione che a due vettori associa uno scalare).

La  definizione di distanza.

Ricordiamo un attimo la definizione di distanza ovvero le proprietà a cui deve  soddisfare d:X x X--->R in un insieme X qualsiasi:

1)d(x,y)

2) d(x,y)=0 se (e soltanto se) x=y

3) d(x,y)=d(y,x) simmetria

4) d(x, y) + d(y, z) ≥ d(x, z) che continuiamo a chiamare diseguaglianza triangolare.

C'è un modo di operare per definire la distanza quando si ha a che fare con spazi con coordinate, (ovvero spazi in cui sia definibile una base ), ed è quella di definire un prodotto , detto scalare, di cui abbiamo tutti sicuramente sentito parlare, e di cui si è parlato più volte in questo sito, però in modo un po' diverso. Ma cominciamo dall'inizio.

Intermezzo: la base di uno spazio vettoriale

Dobbiamo per un attimo  lavorare in  (per adesso in ).  è uno spazio di vettori; ogni punto P di  (o , più in generale, di ) individua un vettore che parte dall'origine O e la cui punta corrisponde al punto P .

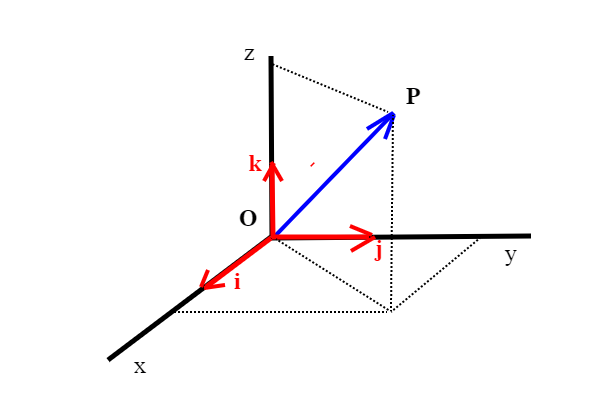
Definiamo in due parole cos'è una base in uno spazio di vettori; sappiamo che , ad esempio in un piano, possiamo scomporre un vettore in due vettori usando la regola del parallelogramma, quindi lungo due direzioni fissate. Chiaramente potremmo farlo anche con tre vettori, scomponendo uno dei due in altri due vettori. Ma noi siamo interessati al numero minimo di  direzioni sufficienti a scomporre tale vettore. Si parla anche di dimensione dello spazio in questione. Nel caso del piano la dimensione è due, nel caso dello spazio euclideo la dimensione è tre. Detto in modo più formale, dato uno spazio di vettori (che possiamo ben immaginare cosa sia) chiamiamo base un insieme di vettori ciascuno dei quali sia non nullo, e che generi tramite combinazioni dette "lineari"*, tutti i  vettori di tale spazio. Per esprimere un vettore tramite una base nel piano, abbiamo bisogno di due direzioni e di due numeri, detti coordinate.Per esprimere un vettore tramite una base nello spazio, abbiamo bisogno di tre direzioni e di tre numeri, detti coordinate.  i,j,k  nella figura è una base dello spazio tridimensionale;

*(esempio di combinazione lineare; dati i vettori  a,b,c e gli scalari x,y,z una  combinazione lineare dei tre vettori è il vettore d= xa + yb +zc)

Calcolare il prodotto scalare usando le coordinate di un vettore.

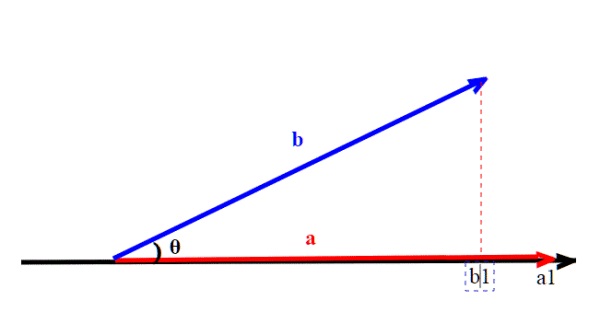
La definizione più nota   di prodotto scalare è la seguente; se indichiamo con |a|, |b| i moduli dei vettori di cui fare il prodotto, e  l'angolo fra di essi, sappiamo che il prodotto scalare (, è dato da :

. Considerato il fatto che ci troviamo in un piano, e avendo a disposizione le coordinate , (assumendo come asse delle x  quello contenente il vettore a) possiamo semplicemente scrivere :

Infatti b1 rappresenta proprio la proiezione di b su a, nonché la coordinata rispetto all'asse x. Ma estendiamo questo discorso alle altre dimensioni:

Per il generico spazio di dimensione n si Ha:

o scritto in modo più compatto, usando il simbolo di sommatoria:

quindi, per n=2 :

per n=3

Notiamo che  il prodotto scalare è simmetrico ()  .

Ma perchè è così importante il prodotto scalare?  Esso ci permette  di definire delle proprietà geometriche importanti, quali la distanza o l'angolo fra due vettori. Vediamo come definire la distanza: introduciamo prima la norma di un vettore (che altro non è che la lunghezza del vettore),in tal modo:

; il radicando è infatti sempre positivo, essendo , ovvero una somma di quadrati.

Per definire poi la distanza fra due punti, prendiamo il vettore(differenza) che li unisce; per trovare la distanza fra i punti individuati dalle punte delle frecce dei vettori a,b, prendiamo la norma della differenza fra i due vettori:

è possibile verificare che la distanza così definita soddisfa le proprietà 1) 2) 3) 4) scritte sopra.

Mettiamoci ora in , e vediamo che  ogni vettore è rappresentabile tramite i vettori ortogonali i,j opportunamente combinati linearmente:

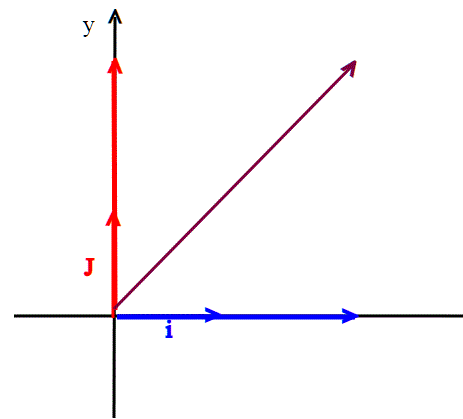
se identifichiamo ogni vettore con una coppia di numeri reali, coordinate delle punte dei vettori, il prodotto scalare risulta una applicazione:

;

ora, se il prodotto scalare è dato dalla formula sopra (per n=2)   ci proponiamo di trovare una matrice, con determinate proprietà, che assumerà una grande importanza nel seguito del discorso. Essa ci permetterà di scrivere in modo compatto le operazioni di questo tipo sui vettori. Se ricordate o qualcuno vi ha mai spiegato quali operazioni si possono fare con una matrice, allora sapete cos'è il prodotto righe per  colonne. Se non lo sapete, allora potete immaginarlo dalla definizione.

Vogliamo trovare una matrice M,  per esprimere il prodotto scalare in forma , per l'appunto , matriciale. Siano a,b due vettori. Possiamo scriverli sia come riga che come colonna.Indichiamo  con  il vettore riga,

 il vettore colonna . Il prodotto scalare vogliamo sia espresso da:

 dove M è la nostra matrice incognita.

Eseguiamo tale prodotto (righe per colonne):

affinché il termine di destra sia uguale al nostro prodotto scalare,, è sufficiente che sia:

che riscriviamo in forma matriciale:

questa è la matrice del prodotto scalare canonico usuale in . Analogamente, in  abbiamo:

Ricordando ciò che abbiamo visto sopra riguardo alla distanza , possiamo concludere che tale distanza è individuata da una matrice M, detta anche tensore metrico. E qui volevamo arrivare; visto così il termine tensore non sembra che spaventi più di tanto. Ma se ne fa un grande uso nella fisica teorica.

Un concetto importante ma di cui mi sono dimenticato:

Autovettori e autovalori

Consideriamo una funzione F fra due spazi vettoriali, V.W:

F: V--->W

un autovettore di una funzione F tra spazi vettoriali è un vettore non nullo la cui immagine è il vettore stesso moltiplicato per un numero (ossia uno scalare) detto autovalore. Se la funzione è lineare, gli autovettori aventi in comune lo stesso autovalore, insieme con il vettore nullo, formano uno spazio vettoriale, detto autospazio.

Riepilogando..

Per definire gli S.H. è fondamentale avere ben chiaro in mente cosa siano:

1. Gli spazi vettoriali
2. La base di uno spazio vettoriale
3. La nozione di distanza e di norma di un vettore, e in definitiva la definizione di spazio metrico.
4. La nozione di prodotto scalare e di ortogonalità. (due vettori sono ortogonali se il loro prodotto scalare è nullo).

Una volta noto il concetto di ortogonalità fra vettori, siamo in grado di definire alcune semplici cose:

Spazio ortogonale. Sia X un sottoinsieme non vuoto di H, spazio vettoriale dotato di un prodotto scalare.
Si chiama spazio ortogonale a X l’insieme
X⊥ = {u ∈ H|u ⊥ x ∀x ∈ X}. Si verifica che X⊥ è un (sotto) spazio vettoriale di H.

Base ortonormale in uno spazio finito dimensionale.
Se H è uno spazio finito dimensionale con prodotto interno, l'insieme  ortonormale U si dice base ortonormale se i vettori di U formano una base di H.

Anche se detto sopra, richiamo ancora la definizione di distanza tramite prodotto scalare.

Distanza generata da un prodotto interno.

; dati i vettori a,b la loro distanza si calcola tramite il prodotto scalare.

Per definire dal punto di vista matematico-formale uno S.H.  ci manca una definizione importante riguardante gli spazi metrici; quella di completezza. Ma cominciamo dall'inizio. Chiamiamo (H,d) il nostro spazio vettoriale munito di una distanza. In esso possiamo parlare di successioni e di convergenza, come si fa in R, insieme dei numeri reali. Al posto del valore assoluto, useremo semplicemente la distanza.

N.B. D'ora in poi indicheremo il prodotto scalare tra u, v che di solito indicavamo con il punto, "v.u"  con una notazione un pò più universale,〈u ,v〉

Per arrivare alla definizione di S.H. bisogna fare un ulteriore ipotesi sulla "completezza"; questo va fatto usando le successioni. A titolo di esempio, Lo spazio R dei numeri reali è completo, mentre invece quello dei razionali Q non lo è; ciò si intuisce  dal fatto che R rappresenta un'estensione dei numeri razionali, atta a riempire certe lacune. Per analizzare la completezza, si usa il presente strumento:

La Successione di Cauchy. Una successione (xn) in H si dice di Cauchy in (H,d) se ∀ ε > 0, ∃n¯ ∈ N tale che :

d(xn, xm) < ε ∀n, m > n¯.

Sappiamo poi che una una successione (xn) è convergente in (H,d) se esiste x ∈ H tale che d(x, xn) → 0 per n → ∞. Questo lo abbiamo visto più volte in questo sito, riguardo ai limiti delle successioni.

Ogni successione convergente è di Cauchy; Non è detto, al contrario, che una successione di Cauchy debba necessariamente convergere né che, se convergente, l'elemento al quale converge appartenga allo spazio in questione.

Prendiamo come esempio la successione:

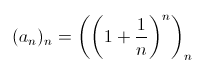
possiamo considerarla come una successione in Q o in R; la successione converge in R, infatti il suo limite:

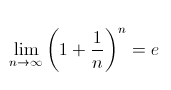
è proprio e, il numero di Nepero. In Q invece non converge, essendo e un numero irrazionale. A questo punto possiamo intuire cosa voglia dire il termine completezza.

Definizione di spazio di Hilbert

Sia H  uno spazio vettoriale con prodotto interno e sia d la metrica indotta dal prodotto scalare . Si dice che H è uno spazio di Hilbert (oppure che è completo) se ogni successione di Cauchy in (H,d) è convergente in (H,d).

Per adesso non pensate al senso di queste definizioni!  Sono necessarie per avere a disposizione delle proprietà che ci permetteranno di raggiungere certi risultati. Insomma, ci serviranno  a posteriori.

Gli spazi euclidei R ⁿ, C ⁿ

sono completi rispetto alla distanza indotta dai loro prodotti interni. Perciò  sono spazi di Hilbert. (credetemi sulla parola!)

Non avremmo fatto tutta questa fatica, per parlare di spazi che già conosciamo. Ma gli S.H. diventano importanti quando la loro dimensione è infinita, e i loro elementi non sono i vettori ordinari dello spazio euclideo.

Spazi di dimensione infinita. Uno spazio V si dice avere dimensione infinita quando non ha dimensione finita, cioè quando, per ogni n ∈ N e per ogni n-pla di vettori v1, ..., vn in V, risulta Span(v1, ..., vn) <> V . Cosa vuol dire Span ecc.,ecc? Semplicemente tutto ciò che viene generato dalle combinazioni lineari dei vettori v1,...vn. In pratica non esiste un insieme finito di vettori che generi V.

Sussiste il seguente risultato, di cui non daremo dimostrazione:

Se H ha dimensione infinita, allora esiste in H una base ortonormale numerabile **

Consideriamo ora come esempio l'insieme delle funzioni a valori  complessi. Lo spazio delle Ψ è formato da elementi che non sono i soliti vettori, ma ne hanno le stesse proprietà algebriche (essenzialmente le proprietà delle operazioni di somma e moltiplicazione per un numero). Un tale spazio astratto (non costituito da vettori ordinari) è detto spazio funzionale perché i suoi elementi sono appunto funzioni. D’ora in poi potremmo chiamare  le funzioni  Ψ anche semplicemente vettori.
Sullo spazio delle Ψ è definito un prodotto interno che (ne omettiamo la dimostrazione) ha le stesse proprietà del prodotto interno (o prodotto scalare) definito sui vettori ordinari. Esattamente, il prodotto interno fra i vettori Ψ1 e Ψ2 è definito da:

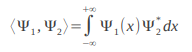
(l'integrale che usiamo  non è quello solito che conosciamo, ma quello di Lebesgue; non c'è niente da preoccuparsi, consente solo di esistere per una gamma più vasta  di funzioni. per il resto, ha le stesse proprietà degli integrali che conosciamo)

dove l’asterisco presente su Ψ2  indica il complesso coniugato. Il prodotto interno così definito presenta le note proprietà. In teoria dovremmo dimostrarle, ma derivano sostanzialmente dalle proprietà degli integrali. Questo è uno spazio di Hilbert, ossia completo, e prende il nome di L² , in onore a Lebesgue.

E’ possibile definire anche la norma (lunghezza) di un vettore come si fa usualmente avendo a  che fare come al solito con un prodotto scalare:

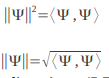
E'  possibile scomporre una funzione (vettore) Ψ nelle sue componenti rispetto ad una base ortonormale? La risposta è  affermativa, ed è data dal teorema **. Inoltre la base ortonormale è numerabile, quindi la funzione può essere espressa come somma di una serie. IL teorema va applicato , come abbiamo visto, agli spazi di dimensione infinita.
Per capire che lo spazio vettoriale delle Ψ è a infinite dimensioni, facciamo l’esempio più semplice dei polinomi di
grado n . Essi costituiscono uno spazio vettoriale a n+1 dimensioni perché per definire un generico polinomio di grado n , ci vogliono n+1 numeri indipendenti (per esempio, se n=2 , i polinomi a0+a1 x+a2 x2 sono individuabili biunivocamente da terne (a0 ,a1 ,a2) , quindi costituiscono uno spazio vettoriale tridimensionale). Detto questo, che dimensione avrà allora lo spazio vettoriale dei polinomi di qualunque grado? Evidentemente infinita, perché fissato un n qualunque, che quindi si avrebbe una dimensione n+1 finita, resterebbero fuori i polinomi di grado >n . Se lo spazio vettoriale dei polinomi di grado qualunque è a infinite dimensioni, a maggior ragione lo sarà lo spazio delle Ψ che è formato da funzioni più generali dei polinomi. Sia allora {Ψk} , con k=1,2,… , una base ortonormale dello spazio delle Ψ , cioè tale per cui: 〈Ψj,Ψk〉=δ jk ,  con j , k=1,2,… , dove δ jk è la delta di Kronecker:
δ jk={ 1 se j=k,  0 se j≠k Un generico vettore Ψ è allora scomponibile rispetto alla suddetta base nel seguente modo:

(le componenti ak si calcolano infatti facendo il prodotto scalare con ciascun  vettore della base ortonormale).

Lo sviluppo si chiama sviluppo in serie di Fourier. Calcoleremo più in dettaglio tali coefficienti usando una particolare base ortonormale. Per ora ci fermiamo qui; al prossima volta approfondiremo le nostre conoscenze sugli spazi di Hilbert e ci occuperemo della trasposizione degli spazi di Hilbert ad applicazioni molto note della fisica.