Equazioni della spirale logaritmica ***

Data l'equazione polare della spirale logaritmica, non è difficile passare alla corrispondente rappresentazione parametrica. Meno immediato è il cammino inverso: da parametrica a polare. Ma percorrendo questo sentiero si può meglio comprendere il significato geometrico dei parametri che stabiliscono la forma della curva.

Nei testi si trova normalmente l'equazione polare della spirale logaritmica, proprio a causa della sua nascita attraverso la funzione logaritmo.

Infatti, scrivere la sua forma più comune:

r = a e^kθ

significa anche scrivere:

ln(r/a) = ln(e^kθ) = kθ

θ = (1/k) ln(r/a)

in cui si vede bene il rapporto logaritmico che vi è tra l'angolo θ e il raggio, ovviamente variabile).

Da queste equazioni si ricavano immediatamente le equazioni parametriche:

x = r cos θ

y = r sen θ

con r funzione dell'angolo θ .

Praticamente introvabile è invece il percorso inverso, ossia partire da equazioni parametriche qualsiasi e ottenere l'equazione polare. Stuzzicato dal povero Pippo alle prese con migliaia di automobiline, trovate di seguito un mio tentativo andato a buon fine...

Trasformazione da coordinate parametriche della spirale logaritmica a coordinate polari

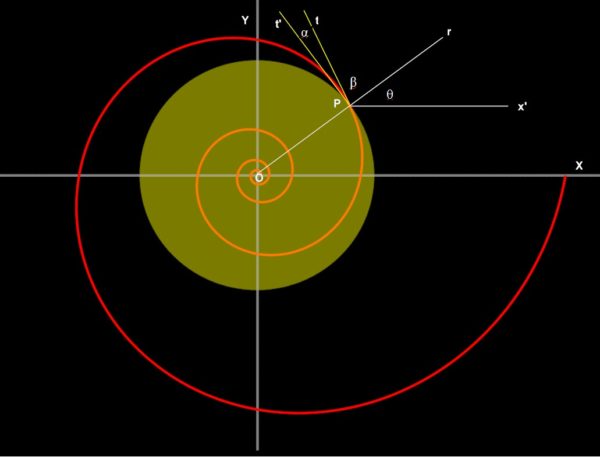
Equazione in coordinate cartesiane della Spirale Logaritmica

$x(\theta) =r(\theta )cos(\theta )$

$y(\theta) =r(\theta )sen(\theta )$

Considero un punto P , intersezione della retta r (raggio OP ) e della curva della spirale logaritmica.

In quel punto P traccio la retta t , tangente alla spirale.

Indico con $\theta$ l'angolo tra r e l'asse orizzontale e con $\beta$ l'angolo fra r e la tangente t .

Il coefficiente angolare della retta t vale $tan (\theta +\beta )$ e lo posso esprimere come rapporto tra le derivate parziali della spirale nel punto P

$tan(\beta+\theta) =\frac{dy}{dx} = \frac{dy}{d\theta } * \frac{d\theta }{dx}$ esplicitando le due derivate di x e y rispetto all'angolo $\theta$ otteniamo

$tan(\beta+\theta ) =\frac{r' sen\theta\ + rcos\theta }{r'cos\theta -rsen\theta } =$

$=\frac{r'sen\theta {cos\theta }/{cos\theta } + rcos\theta }{r'cos\theta -rsen\theta cos\theta /cos\theta }$ $=\frac{r'tan\theta{cos\theta } + rcos\theta }{r'cos\theta -rtan\theta cos\theta }$ $=\frac{rcos\theta (r'tan\theta/r +1)}{r'cos\theta( 1-rtan\theta/r') }$ =

$=\frac{rcos\theta (tan\theta +r/r')}{r cos\theta( 1-rtan\theta/r') }$ $=\frac{tan\theta +r/r'}{1-tan\theta r/r'}$ = $tan(\theta +\beta )$ da cui ricavo:

$tan(\theta )+\frac{r}{r'}=tan(\theta +\beta )-tan(\theta +\beta)tan\theta \frac{r}{r'}$

$tan\theta -tan(\theta +\beta ) =-\frac{r}{r'}(tan(\theta +\beta ) + 1)$

$\frac{tan(\theta +\beta)-tan\theta}{1+tan(\theta +\beta )tan(\theta )}=\frac{r}{r'}$

Ricordando le formule che legano il seno e il coseno della somma di due angoli con i seni e i coseni dei due angoli (e ricordando che la tangente è uguale al seno diviso per il coseno), ci accorgiamo che il termine a sinistra non è altro che lo sviluppo della tangente della differenza tra i due angoli $(\theta +\beta)$ e $\beta$ ossia precisamente $tan\beta$ .