La soluzione del quiz di Pippo e del solito Nobody. Benché sembri impossibile, a prima vista, anche al buio, il nostro eroe sarebbe capace di catturare non una ma infinite automobiline che si dirigono ognuna in una direzione diversa  verso le pareti con velocità costante. Non ci riesce ricordando Archimede, ma ci riesce passando alla "spira mirabilis" di Bernoulli. La soluzione è stata soprattutto elaborata e scritta da Maurizio che ama le spirali più che il suo amico Pautasso i marroni!

"Riuscire ad essere nel posto giusto al momento giusto produce lo stesso risultato di essere in più posti nello stesso istante, cosa notoriamente impossibile.  Non potendo essere presente contemporaneamente su ciascun punto di una circonferenza che si dilata, per intercettare gli infiniti raggi della sua espansione, li fronteggerò ad uno ad uno, istante dopo istante, spostandomi su una opportuna curva, attorno alla circonferenza. Sarà come se quella curva avesse fermato il tempo"

(Pippo)

 

Se volete provare a risolvere il quiz prima di leggere la soluzione, lo trovate QUI.

 

Nel momento in cui la luce si spegne Pippo sa che l'automobilina inizia a spostarsi alla velocità di 78 cm/s in una direzione che sarà immutabile.

Lui è notevolmente più veloce, può muoversi a 214 cm/s costantemente, anche su una linea curva.

Mentre Nobody gli mostrava, ridacchiando sguaiatamente, la minuscola auto telecomandata, ha avuto modo di valutare la distanza tra lui e il centro del locale, dove è piazzato il veicolo, giusto 10,5 metri.

Se l'auto venisse direttamente verso di lui, andandole incontro la  potrebbe bloccare facilmente. Si incontrerebbero, in un ben preciso punto P', determinabile immediatamente.

Infatti, l'auto ha percorso OP' con velocità Va, impiegando un certo tempo, mentre Pippo, in quel medesimo tempo ha percorso PP' a velocità Vp.

a pari tempo:         OP': Va = PP' : Vp

equivalente a        (OP-PP') : Va = PP':Vp

ed essendo             PP' = Vp OP = (Va + Vp) PP'

si ricava                  PP' = OP Vp/(Va+Vp) = 10,5 * 214/ 292 = 7,7 m

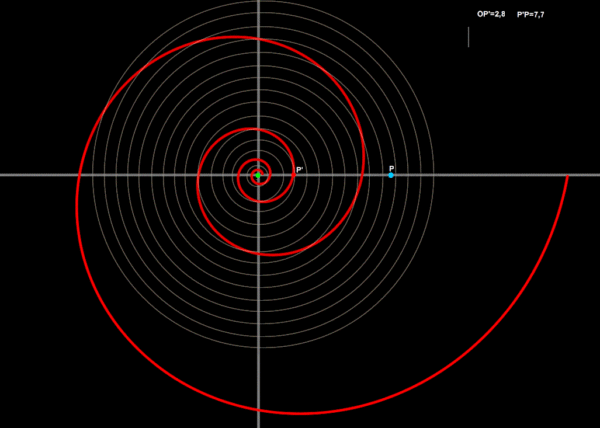
Percorsi questi 7,7 metri, Pippo ha due possibilità: o si ritrova tra le mani l'auto, oppure non trova nulla. In questo caso sa con certezza che la distanza dell'auto dal centro O, in quel preciso istante, è pari alla differenza 10,5 - 7,7 = 2,8 metri.

Quello che non sa ancora è in quale punto della circonferenza di centro in O e di raggio 2,8 m è situato il pericoloso giocattolo, con sopra le chiavi per aprire la porta e poter uscire.

Se potesse trovarsi contemporaneamente in ogni punto della circonferenza intercetterebbe l'auto, ma per raggiungere un qualsiasi punto, anche il più vicino, occorre un certo tempo e in questo tempo l'auto si è già spostata.

Gli resta solo la possibilità di portarsi sul raggio più vicino, puntando contemporaneamente ad un cerchio più esterno di quello su cui si trovano in quel preciso momento tutte le possibili automobili e lui stesso.

Se non avrà successo, dovrà riprovare, puntando alla intersezione tra un raggio successivo e una circonferenza di raggio maggiore ( perché intanto l'auto si è ulteriormente allontanata dal centro).

E continuare in questo modo, ruotando attorno ad O e allargandosi, fino ad intercettare l'auto.

Se si potesse fare  una radiografia dei pensieri di Pippo in questo momento vedremmo questa immagine  (non dimenticate che il ragazzo ha cominciato molto precocemente a sviluppare il suo senso matematico ed è naturale che "pensi" su carta a quadretti ) :

Ma come sapere verso quale punto preciso dirigersi di volta in volta?

 

Orbite concentriche e loro attraversamento

Osserviamo attentamente  questa figura

 

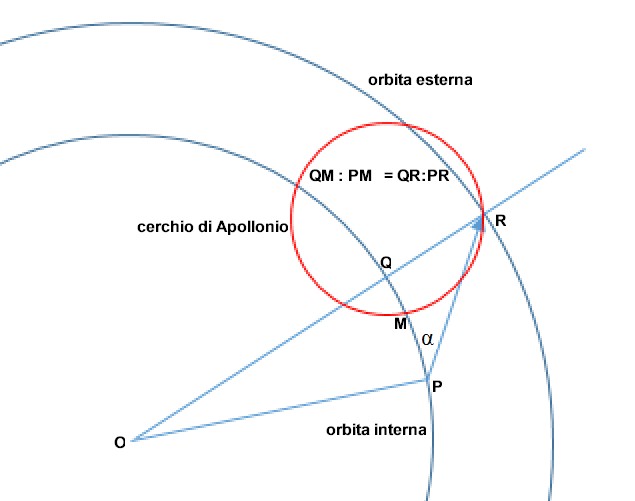
Usiamo la parola orbita per definire ciascun cerchio concentrico come quello che passa per P, in cui supponiamo si trovi Pippo

La direzione OP sia il riferimento per le angolazioni dei raggi successivi che hanno tutti  centro O.

Esploriamo il raggio che forma con il riferimento un angolo  piccolo a piacere e ipotizziamo  che l'auto si trovi su di esso, in movimento radiale  con velocità Va.  Pippo la può facilmente raggiungere, spostandosi da P con la sua velocità Vp > Va,  staccandosi dell'orbita interna e andando a "tagliare la strada all'auto".  Ma la direzione da tenere, con velocità costante va determinata con precisione.

Per sapere dove puntare basterebbe costruire con gli elementi noti il cerchio (rosso) di Apollonio  (già incontrato QUI) che nella figura  passa per il punto intermedio  (M)  tra Pippo   (P)  e l'auto  (Q) , con la solita ripartizione delle distanze, proporzionali alle rispettive velocità:  Vp e Va.

Essendo noto tale rapporto e la direzione dell'auto, si determina univocamente il punto di intercettazione (R) che individuerà la nuova orbita esterna.

Il percorso di Pippo sarà la ipotenusa di un triangolo rettangolo che ha un cateto radiale (QR =direzione auto) e uno tangenziale ( QP ) all'orbita occupata, quella definita "interna".

Il rapporto tra le due componenti è la tangente dell'angolo alfa di distacco dall'orbita attuale per andare al punto di incontro.

Possiamo calcolare tan(alfa) , facendo riferimento alle velocità.

Anche se stiamo ragionando solo su una ipotesi (siamo al buio) l'angolo che abbiamo calcolato è quello che ci garantisce di giungere (su una scala infinitesima) al punto giusto nel momento giusto. Se l'auto fosse davvero su quella direttrice, verrebbe ineluttabilmente catturata. Se non è su quella direttrice occorrerà reiterare la procedura per il passo (infinitesimo) successivo. Insomma è la geometria “intrinseca” del sistema, dettata dal rapporto delle velocità, che determina la strategia e la meccanica dello spostamento.

Se l'angolo fosse più piccolo di alfa, Pippo, con la sua velocità Vp, passerebbe in anticipo sull'auto, viceversa con un angolo più grande passerebbe in ritardo. Solo con quell'angolo arriva al momento esatto del transito dell'auto.

La successione degli spostamenti disegna una curva a forma di spirale ad angolo costante, una spirale “equiangolare”.

 

Il punto P si trova sulla retta r .  Il raggio della spirale è dato dalla distanza OP  ed è uguale al raggio della orbita attualmente occupata.

L'angolo compreso tra la retta t  tangente alla spirale e la retta t', tangente all'orbita, è l'angolo di "distacco" alfa e di "accrescimento del raggio" che caratterizza, mantenendosi costante in ogni punto, la forma della spirale.

La differenza tra questa spirale e quella di Archimede è che in quest'ultima ad incrementi uguali dell'angolo di rotazione corrispondono uguali incrementi del raggio. Questo significa che ad ogni giro completo la crescita del raggio è sempre la stessa. Ora domandiamoci di quanto aumenta la lunghezza di una spirale di Archimede  ad ogni giro. Il rapporto tra lo sviluppo di una singola spira e lo sviluppo della spira successiva è costante. Di conseguenza l'aumento di lunghezza tra una spira e la successiva risulterà ogni volta diverso, in particolare crescente.

Il rapporto tra la crescita radiale ( costante)  e lunghezza della spira (crescente) sarà un valore decrescente ad ogni giro, e questo rapporto è legato all'angolo di distacco della spirale, quello che abbiamo chiamato alfa.

In conclusione la spirale di Archimede non è una spirale equiangola, ad ogni incremento di rotazione cala il suo angolo alfa.

Solo modulando opportunamente la velocità,  Pippo riuscirebbe ad arrivare puntuale all'incontro con l'automobilina. Ma abbiamo il vincolo che  la sua velocità non può essere variabile.

Per mantenere l'angolo alfa costante la misura radiale della spirale deve crescere con lo stesso fattore moltiplicativo della base.

Il passo della spirale di Archimede è dato dalla differenza costante tra le misure dei raggi a inizio e fine di un giro. Il passo della spirale equiangola è invece  dato dal rapporto costante tra i raggi a inizio e fine giro.

Percorrendo la spirale di Archimede a velocità costante si perde subito il sincronismo con la dinamica di crescita dei raggi, sincronismo che invece si conserva con la spirale equiangola. Per convincersene basta pensare di sovrapporre le due spirali, come vediamo qui sotto: La pigrizia con cui si sviluppa la spirale di Archimede ( nera)  è evidente e fatale per la sua efficacia nel raggiungere il punto giusto al momento giusto Più cresce il raggio e più la Spirale di Archimede assomiglia ad un cerchio, mentre la spirale logaritmica per la  sua  intrinseca "autosomiglianza"  non cambia fisionomia.

Quindi la spirale di Archimede non è “adatta” allo scopo.

Se non ne siete del tutto convinti proviamo a impostare il ragionamento in questo altro modo...

Immaginiamo pure che le automobiline siano in numero anche infinito (o, perlomeno, molto grande). Ognuna di loro parte nello stesso momento da un punto che scegliamo come origine. Iniziamo col considerare la macchina che va proprio in direzione di Pippo. Lei viaggia con una certa velocità Va, mentre Pippo va verso di lei, ossia verso il punto in cui ha visto per l’ultima volta le automobiline (consideriamole pure molto piccole dato che devono stare tutte nella stessa posizione iniziale) con la sua velocità Vp, Pippo incontrerà sicuramente l’automobilina “suicida” dopo un certo tempo T.

Ne segue che la somma dello spazio percorso da Pippo e di quello percorso dall’automobilina deve essere uguale alla distanza D iniziale tra Pippo e l’auto.

D = VaT + VpT

Sono tutte quantità note tranne T che può essere facilmente calcolato

T = D/(Va+Vp)

Noto T è anche nota la distanza del punto d’incontro rispetto all’origine (ossia lo spazio percorso dalla prima automobilina).

Ro = Va T

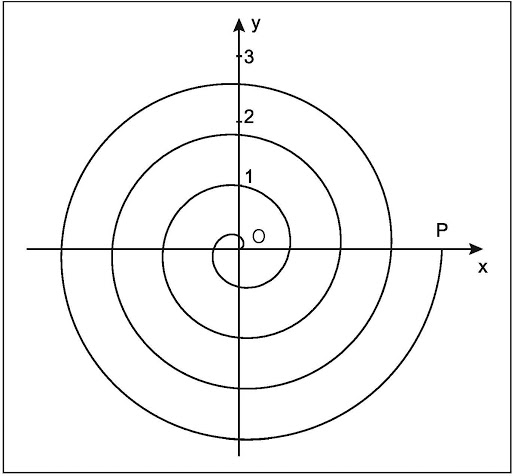
Pippo cattura la prima automobilina, ma intanto le altre stanno proseguendo il loro cammino verso le pareti. Nessun problema. Pippo sa benissimo che esiste una curva che, a partire da Ro, si allarga sempre più al variare dell’angolo ϑ (misurato rispetto alla congiungente origine-Pippo iniziale) che varia col tempo. Poco importa quale sia la direzione sia antioraria che oraria.

Questa curva “potrebbe” essere la spirale di Archimede. Sappiamo che questa particolare spirale si allarga mantenendo però costante la distanza tra le sue spire. Ossia ha un’equazione del tipo:

r = p ϑ + Ro

Quanto teta = 0, r = Ro, quando teta = 2π, r = p 2π + Ro

In altre parole, quando Pippo ritorna sull’asse x, si è allontanato rispetto a Ro della distanza:

r = p 2π + Ro - Ro = 2 p π

p è una costante, che sarà sempre la stessa al secondo, al terzo, al quarto giro di Pippo. E’ vero che lui continua a scandagliare tutta la stanza allargandosi sempre un po’ (e di quanto si allarga ce lo dice la costante p), ma le automobiline non stanno ferme. Prendiamo ad esempio quella che si è mossa in verso opposto alla prima.

Il percorso che ha compiuto è pari a r₂ = 2 Va T₂ = 2 Ro

Il percorso che deve compiere Pippo per arrivare esattamente in quel punto al tempo T₂ deve essere uguale alla lunghezza della spirale di Archimede percorsa con velocità Vp. Tuttavia, ciò che vogliamo è che Pippo raggiunga anche la seconda automobilina nel punto giusto e al momento giusto. Ossia nello stesso T₂ deve giungere in r₂. Ma come posso scrivere il suo r₂?

r₂= p π + Ro

uguagliando otteniamo:

2Ro = pπ + Ro

Ossia la costante p risulta essere:

p = Ro/π

Bene… se la velocità è abbastanza alta potrebbe anche farcela, ma… cosa succederebbe per la prima automobilina, quella che ha già catturato, ma che avrebbe anche potuto lasciarsi per ultima?

Lei ha percorso quattro volte Ro, mentre per arrivare con la spirale di Archimede in tempo per catturarla deve valere la relazione:

p 2π + Ro = 4 Ro

Proviamo a ricavare p …

p = 3Ro/2

eh no! Se utilizzasse la spirale di Archimede Pippo dovrebbe avere p costante e invece abbiamo visto che per raggiungere le due automobili deve cambiare p.

D’altra parte se Pippo usasse la spirale di Archimede per prendere la seconda automobilina il suo p sarebbe Ro/π

Se completasse il giro con quella costante arriverebbe a

R₃ = 2Roπ/π + Ro = 3Ro. Buum! Al suo ritorno sull’asse delle x positivo la macchina avrebbe già percorso 4Ro. Anche se Pippo avesse catturato la prima e la seconda non riuscirebbe sicuramente a catturare quella partita verso una direzione inclinata di anche solo un dϑ piccolo a piacere

Diamo i numeri (del problema)

Dopo questa verifica torniamo alla spirale equiangola e a come rappresentare le coordinate dei suoi punti.

le sue equazioni parametriche sono le seguenti:

Esse ci dicono semplicemente che il raggio r varia in funzione dell'angolo di rotazione teta e le due coordinate cartesiane x e y sono la proiezione del suo estremo sugli assi.

Questa coppia di equazioni può essere trasformata in una equivalente equazione polare, mettendo in evidenza la struttura esponenziale dell' accrescimento progressivo del raggio, in funzione della sua rotazione.

Questa diversa rappresentazione contiene parametri che sono direttamente riconducibili alla misura del raggio iniziale  (a)  e alla tangente dell'angolo di accrescimento (k).

Dalla forma esponenziale che dà il raggio in funzione dell'angolo (teta) e dei due parametri a e k , si può  infine passare alla espressione esplicita di teta:

 θ = 1/k ln(r/a)

Si tratta ovviamente di una funzione logaritmica e questo spiega il motivo per cui la spirale equiangola è detta logaritmica.

Tralasciando i passaggi analitici, ma volendo prevedere le coordinate di intercettazione e l'istante in cui essa si verifica, possiamo operare direttamente sulle equazioni parametriche.

Ripetiamo ancora una volta cosa rappresentano i parametri a e k.

Con il simbolo a si intende la misura del raggio della spirale nel punto iniziale, nel nostro caso la distanza tra il centro della stanza A e la posizione P' in cui si Pippo dopo avere percorso la distanza PP' nel tempo T trascorso dallo spegnimento della luce

Se ricordate questa distanza, AP', misura 2,8 m

Con il simbolo k si intende il valore della tangente dell'angolo di accrescimento alfa

questo valore è espresso dalla relazione tra le velocità Va e Vp

             numericamente: k = 0,391         ( alfa = 21,4°)

Le coordinate del punto di incontro si ottengono  dalle equazioni della spirale in cui è stato inserito il valore di angolo teta della traiettoria dell’auto = tetauto.

il passo della spirale è dato da      e ^0.391·2π = 11,65         ed è un fattore moltiplicativo

L'unico dato che resta non disponibile è proprio la direzione dell'auto (tetauto) ma siamo in grado di disegnare tutto l'arco di spirale, semplicemente facendolo variare da 0 a 2, e trovare le coordinate Xi, Yi, di un qualsiasi punto di intercettazione.

il tempo di intercettazione, dall'istante di spegnimento della luce, si ricava dal rapporto T = d/Va tra la distanza

             percorsa dalla auto, e la sua velocità Va.

 

Fidarsi non è bene e non fidarsi è sicuramente meglio

Raccolte le chiavi,  Pippo prosegue la corsa fino a completare il giro attorno ad O , senza fermarsi né rallentare. Per farvelo vedere proprio "dal vero" abbiamo rapinato questa illuminante animazione dal commento di Fabrizio al quiz.  Dice praticamente tutto.

 

 

Perché  Pippo, dopo avere recuperato le chiavi, non si dirige immediatamente verso la porta?

Il motivo è semplice ed anche un po' raccapricciante.

Il diabolico Nobody potrebbe avere concepito un veicolo composito, in grado di scindersi in due o più parti. Se così fosse, le auto in movimento, con direzioni diverse, sarebbero almeno due. L'intercettazione di un'auto non ferma le altre. Se Pippo non completasse il giro per accertarsi che non vi sia questo rischio ed eventualmente eseguire le altre catture, una ipotetica “seconda auto” potrebbe proseguire la sua corsa verso il muro e, impattandolo, innescherebbe l'esplosione.

A Pippo non la si fa...

P.S.: dicono che, quando Archimede ha saputo del fatto, sia rimasto da solo nella sua stanza, furente, inveendo contro non si sa che cosa. Sembra anche che abbia trovato un po' di pace quando è arrivato Apollonio a tirargli su il morale. Non tutte le spirali riescono con il... BUCO giusto!