Categorie: Arte e letteratura Matematica Storia della Scienza
Tags: architettura armonia linguaggio monaci cistercensi numeri
Scritto da: Vincenzo Zappalà
Commenti:9
I numeri... cistercensi **
Questo articolo è stato inserito nelle sezioni d'archivio "Matematica e geometria", "Storia della Scienza" e "Arte e Letteratura"
Sempre di linguaggio parliamo, ma questa volta di quello "numerico". Ne scopriamo uno adottato con grande inventiva dai monaci cistercensi, capaci di creare non solo meravigliosi monumenti, ma anche simboli molto arguti!
I monasteri con le loro regole più o meno severe hanno sicuramente contribuito allo sviluppo della cultura attraverso il medioevo. Molti manoscritti antichi sono pervenuti fino a noi proprio grazie al lavoro incessante di scrittura e di catalogazione dei monaci. Non parliamo poi degli splendidi edifici monastici che ci hanno consegnato capolavori di architettura, scultura e pittura straordinari. Ovviamente, le scelte e le regole non sempre erano "perfette" per la cultura in genere, ma bisogna dare a Cesare quello che è di Cesare...
Particolare risalto assume la figura di San Benedetto da Norcia, che dopo un inizio eremitico fondò il suo ordine, spesso sintetizzato nella frase celeberrima: "Ora et labora" (Prega e lavora). Ho avuto la fortuna, quest'anno, di visitare il Sacro Speco vicino a Subiaco, dove Benedetto passò alcuni anni di vita eremitica e vi posso assicurare che è ancora uno scrigno di bellezza, armonia e arditezza.

La scarsità di turisti ha anche messo in particolare luce le caratteristiche fondamentali dell'ordine: semplicità, silenzio, ammirazione e lavoro.
Proprio alle regole di San Benedetto si collega l'ordine dei Cistercensi, fondato alla fine dell'anno mille. Le chiese, i chiostri, le sale capitolari sono esempi fantastici di armonia "povera", dove il contributo di statue e immagini è ridotto al minimo ed è proprio la semplicità, il rigore e lo slancio dei moduli architettonici a imprimere un segno del tutto particolare, in un periodo in cui il gotico stava imponendosi sempre più impreziosito da sculture, vetrate multicolori e ornamenti molto elaborati.
Quasi tutti gli edifici cistercensi, che erano stati eretti in tutta Europa, sono andati distrutti a seguito della Rivoluzione Francese, ma l'Italia ne conserva ancora qualche esempio meraviglioso. Tra queste fatemi citare i tre capolavori più suggestivi e meglio conservati: le Abbazie di Casamari e Fossanova, nel Lazio, e lo spettacolare rudere di San Galgano in Toscana.



Gli interni delle chiese impressionano per la nitidezza delle line che sembrano portare direttamente verso l'alto. A questo riguardo merita assistere al tramonto presso San Galgano fino alla comparsa delle stelle. La chiesa è completamente scoperchiata e assistere alle prime luci dell'Universo, seguendo la direzione di quelle colonne, bellissime nella loro semplicità, è come seguire una linea diretta che unisce la vita terrena all'Universo. Un momento di purissima preghiera "laica".

Lo schema ricorrente degli edifici cistercensi è improntato anch'esso a poche regole geometriche, basate sul quadrato e sul triangolo, come mostra lo schema che riporto di seguito.
In ogni caso, per tornare allo scopo principale di questo articolo, i cistercensi accentuano ancora di più la regola di Benedetto e fanno del silenzio, della meditazione e del lavoro dei campi i punti essenziali della loro vita. Sembra che per comunicare tra di loro usassero segni, una specie di linguaggio dei muti. Ma, scoperta abbastanza recente e ancora in fase di studio, è il sistema di numerazione che usavano.
I numeri non gli servivano per fare calcoli matematici, ma per ricordare e segnalare date particolari, per numerare pagine e manoscritti, per indicare luoghi e cento altri indicatori pratici. Ormai era stato praticamente abbandonato il sistema numerico romano e i numeri arabi avevano fatto il loro ingresso prepotente in tutta Europa: semplici, limitati, capaci di permettere operazioni più o meno complicate. La base 10 era diventata la norma per tutto l'occidente.
Ebbene, i cistercensi si erano creati un sistema numerico tutto particolare, anch'esso a base decimale, ma basato su segni all'apparenza senza alcun ordine, che permettevano di poter codificare e comunicare tra loro in un linguaggio cifrato ed esclusivo. Non potevano superare il numero 9999, ossia le quattro cifre, più che sufficiente, però, per indicare le date, i libri, le pagine e molto altro. Bene, vogliamo impararlo anche noi? Chissà che non venga utile per potere scambiarsi indicazioni numeriche in un mondo che ci sta portando verso abissi difficili da immaginare.
Proviamo a scrivere il numero 1234 in numeri romani:
MCCXXXIV
Un po'lungo e complicato, sicuramente!
Scriviamolo in numeri arabi:
1234
Beh... sicuramente più compatto, ma sempre e comunque composto da quattro simboli.
Vediamo, invece, come l'avrebbero scritto i cistercensi:
Meraviglioso, un solo simbolo! L'ideale, sicuramente, per le loro motivazioni che non prevedevano calcoli, ma solo date, pagine e cose del genere, limitandosi solo a numeri di 4 cifre.
Entriamo, allora, nel loro mondo "simbolico"...
Iniziamo con i primi dieci numeri, dallo zero al nove. Poi sarà facile eseguire le combinazioni per esprimere le decine, le centinaia e le migliaia.
Lo zero è un segmento verticale, il segno più semplice. A questo segmento vengono aggiunti dei semplici segni geometrici per costruire i nove numeri successivi. Vediamoli nella Fig. 1 :
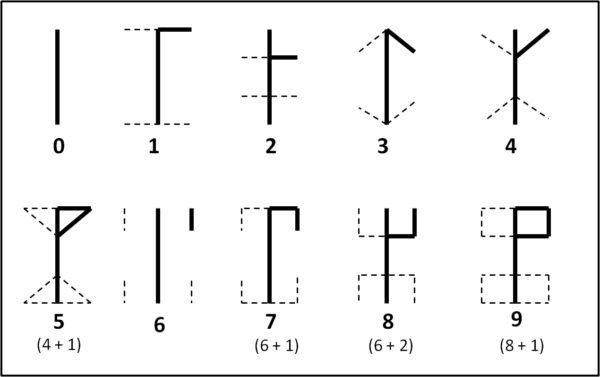
Analizziamola con attenzione... In grassetto sono disegnati i simboli "standard". Alcuni di loro sono proprio le combinazioni di due simboli (il 5 è il simbolo del 4 con la sovrapposizione del simbolo dell'1; il simbolo del 7 è la sovrapposizione del simbolo del 6 al simbolo dell'1; ecc.), ma si può anche notare che per ognuno di essi (tranne ovviamente lo zero) sono stati tracciate alcune linee a tratteggio. Potremmo dire che esse danno luogo a simboli alternativi del tutto equivalenti. Prendiamo, ad esempio, il numero 3, ma potremmo ripeterlo per chiunque altro: se il piccolo segmento inclinato posto in alto verso destra fosse trasportato in alto averso sinistra, oppure in basso verso destra o verso sinistra, la sua caratteristica rimarrebbe comunque sempre la stessa, NON confondibile con altri simboli numerici. In realtà, le posizioni assunte dai segmenti che si aggiungono a quello base dello zero (segmento lungo verticale) significano molto, pur rimanendo sempre legate a un solo numero.
Spieghiamolo meglio attraverso la Fig. 2:
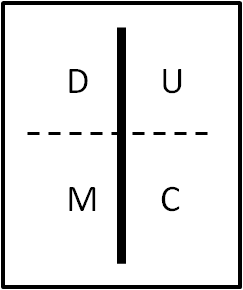
Consideriamo lo zero e tracciamo idealmente una linea orizzontale tratteggiata che venga a dividere il nostro spazio a disposizione in quattro parti. Bene, ad ognuna di queste quattro parti viene associata l'unità, la decina, il centinaio e il migliaio (U,D,C,M). L'ordine è quello che è stato scritto nei quattro riquadri.
A questo punto ogni numero con i suoi piccoli tratti caratteristici che si sono rappresentati nella figura 1, può dar luogo alle unità, alle decine, alle centinaia e alle migliaia, a seconda del riquadro in cui venga inserito, variando conseguentemente l'orientamento dei segmenti caratteristici di quel dato numero. Meglio la Fig. 3 (parte alta) piuttosto che tante parole.
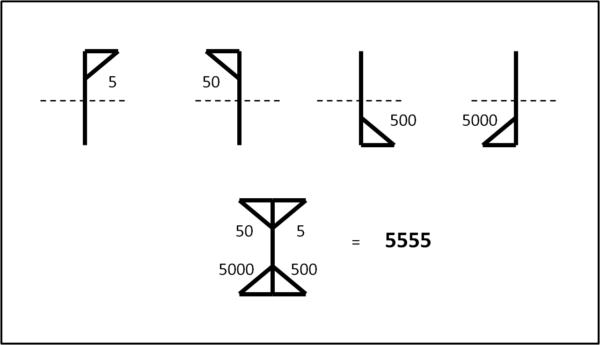
Ne consegue che diventa facilissimo scrivere sia il 5, che il 50, che il 500, che il 5000, così come, ad esempio, il 5555 (parte bassa della Fig. 3). Non si rischiano confusioni con altri numeri, date le caratteristiche dei trattini aggiuntivi, qualunque sia la loro posizione od orientamento.
Scriviamo in Fig. 4 il numero iniziale, ossia il 1234 e vediamone la costruzione.
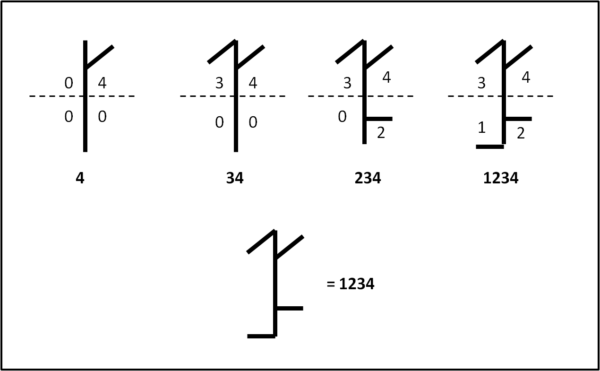
Cominciamo con il riquadro delle unità (in alto a destra) dove inseriamo il numero corrispondente, ossia 4. Poi passiamo alle decine (in alto a sinistra) dove inseriamo il 3; scendiamo al livello inferiore e a destra inseriamo le centinaia, ossia il numero 2 e, infine, nel riquadro rimasto, inseriamo le migliaia, ossia il numero 1. Se in un certo riquadro non appare nessun segmento aggiuntivo vuol dire che assume il valore 0. In pratica, per arrivare a 1234, siamo passati da 4 a 34 a 234 e, infine a 1234.
A questo punto, diventa facilissimo rappresentare qualsiasi numero da o a 9999. Nella Fig. 5, che segue, ad esempio, c'è il mio anno di nascita...
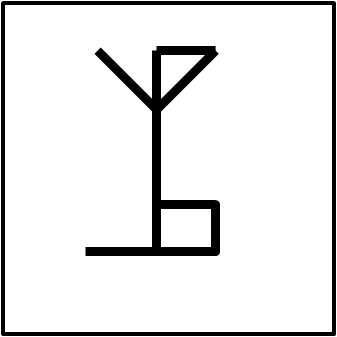
Adesso potete divertirvi a scrivere qualsiasi numero di quattro cifre (o anche meno) vogliate... e rimarrà un segreto tra noi (e i cistercensi...).
Bibliografia:
David A King, The Ciphers of the Monks – A forgotten number notation of the Middle Ages, Stuttgart: Steiner, 200








9 commenti
Geniale :-)
Chissà se avevano anche l'esigenza di apporre segni aggiuntivi per indicare il sotto o il sopra della cifra.
scusa Giuseppe, non ho capito cosa intendi con sopra e sotto... il sotto dell'ideale sezione divisa in quattro è sempre quella in basso...
Ah! Mi scuso per la mia poca chiarezza. Avevo in mente il verso.
Ho immaginato che un monaco si dirige ansiosamente verso un suo confratello dalle doti profetiche e chiede: “Non tenerci sulle spine, fratello, in che anno nascerà quell'uomo da te profetizzato che parlerà a tutti delle stelle ed assillerà le genti con enigmi di matematica sapienza e favellerà di vino?”.
Il confratello profeta gli riponde che la data si trova nella sua cella. Il primo monaco entra nella cella e vede la Fig. 5 scritta su foglio bianco...
O altre situazioni:
Un monaco chiede all’altro: Quanto ti devo?....
oppure i monaci organizzano una lotteria con quei numeri...
ecc...
Giusto mi chiedevo se esistessero situazioni pratiche nelle quali c'era bisogno di specificare il verso.
sei troppo simpatico Giuseppe!
Adesso ho capito... boh, forse mettevano una freccia?
1234 siamo sicuri che il 3 sia giusto?
Ciao Danilo,
visto che il prof non può risponderti subito perché rientrerà fra qualche giorno, ho provato a cercare l’errore che ci segnali, ma non l’ho trovato.
Ci dici qual è, per favore?
sono Danilo,
ho controllato e nessun errore o meglio, l' errore è stato mio.
mi scuso e , nel caso, cancellate il mio intervento senza problemi.
Nessun problema, Danilo, capita a tutti di sbagliare e, come ben sanno i lettori più assidui, anche a noi capita spesso