Categorie: Matematica
Tags: Brahmagupta Erone quadrilatero quadrilatero inscritto circonferenza
Scritto da: Vincenzo Zappalà
Commenti:0
Brahmagupta: Erone si fa in.... quattro (prima parte) ****
Questo articolo è inserito in Matematica e Geometria
Non spaventatevi dei quattro asterischi... Essi non sono dovuti a calcoli complessi o a nozioni che sono bagaglio di pochi. Tutta la dimostrazione del problema si basa su una geometria veramente semplice così come è elementare quel po' di matematica che la condisce. Il vero problema è scovare le giuste relazioni tra le grandezze in gioco. Un modo divertente per dare il giusto rilievo a un grande matematico indiano, Brahmagupta. Il nostro Leandro, vero mago matematico, conosceva la formula e, magari, potrebbe anche trovare un metodo alternativo di dimostrazione
Parliamo spesso e volentieri di Pitagora, Archimede e via dicendo, ma ben poco dei grandi matematici indiani. La considero una grossa lacuna e cercherò di rimediare. Cominciamo con il grande Brahmagupta (598 – 668 d.C.). Conviene leggere la sua storia scientifica su Wikipedia italiano e ancor meglio su quello inglese, dove i suoi contributi in vari campi della Scienza sono descritti in modo nettamente più esteso.
Importantissima è la cosiddetta "Formula di Brahmagupta" relativa al calcolo dell'area di un quadrilatero qualsiasi iscritto in una circonferenza (detto anche quadrilatero ciclico). Una formula che ci ricorda da vicino quella di Erone, relativa al triangolo. Anzi, quella di Erone è un caso particolare (molto ben conosciuto) del caso più generale di Brahmagupta (ben poco -e ingiustamente- conosciuta e insegnata).
Essa dice:
Area (ABCD) = K = √((s -a)(s - b)(s - c)(s -d))
dove a, b, c e d sono i quattro lati del quadrilatero ciclico ABCD e s è il suo semiperimetro. Risulta ovvio che se il quadrilatero si riduce a un triangolo (a, b, c) abbiamo d = 0 e la formula precedente diventa la ben più celebre formula di Erone. Ne consegue che la formula di Erone non è altro che un suo caso particolare.
La formula di B. può essere ricavata in almeno due modi ed è stata affrontata da molti matematici posteriori. Tuttavia, i due metodi usano la trigonometria oppure danno come acquisita la conoscenza della formula di Erone. La faccenda non mi dava soddisfazione e ho cercato di trovare una dimostrazione basata solo sulla geometria, dato che il grande matematico indiano non poteva ancora utilizzare la trigonometria e ben difficilmente avrebbe usato una formula particolare (sempre che la conoscesse) per ottenere quella generale. Quale sarà mai stata la sua dimostrazione? Non credo che lo sapremo mai, ma il metodo trovato appare brillante e fantasioso anche se abbastanza lungo e complesso. Vale la pena descriverlo, rendendo comprensibili tutti i passaggi, alcuni dei quali veramente divertenti. Chi ama la geometria è servito!
Dividiamo la dimostrazione in vari "blocchi", ciascuno dei quali permette di avvicinarsi al grande finale.
(A) Consideriamo un quadrilatero ciclico ABCD di lati a, b, c e d e prolunghiamo i lati b e d fino a incontrarsi nel punto V. Costruiamo anche le due circonferenze tangenti ai lati a e c e ai prolungamenti dei lati b e d (Fig. 1).
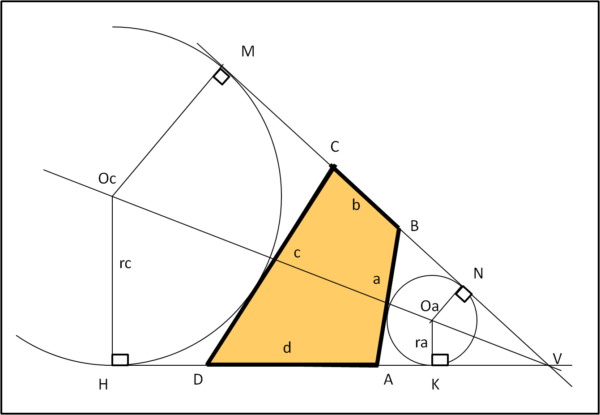
I triangoli OcMV e OcHV sono congruenti (triangoli rettangoli con due lati congruenti). Ne segue che MV = HV e, di conseguenza, sono congruenti i lati MN e HK, che chiamiamo s (vedremo poi perché). Ma, allora, i due quadrilateri MNOaOc (verde) e OaOcHK (giallo) sono congruenti, avendo tre lati e i due angoli tra essi compresi congruenti. (Fig. 2).
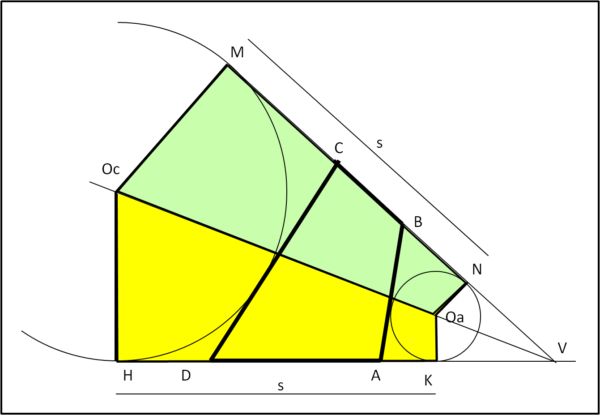
A questo punto possiamo "ribaltare" il quadrilatero verde attorno all'asse x, perpendicolare a OcOa (Fig. 3), ottenendo il rettangolo N'M'HK.
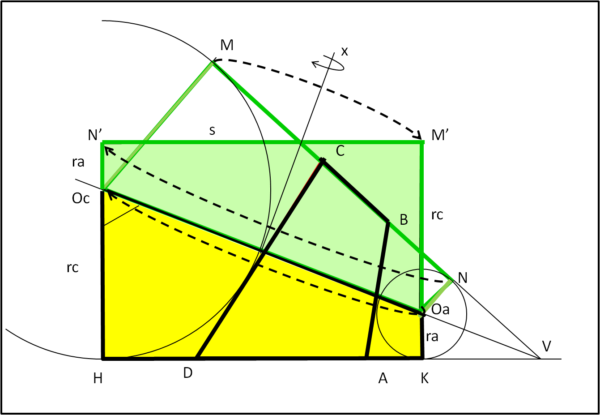
Ne segue che la somma delle aree de due quadrilateri (verde e giallo), uguali tra loro, è uguale all'area del rettangolo N'M'HK e, quindi, vale:
A(N'M'HK) = A(2MNOaOc) = (ra + rc) s .... (1)
(B) A questo punto spieghiamo perché abbiamo chiamato s i lati KH e MN. Lo mostra molto bene la Fig. 4.
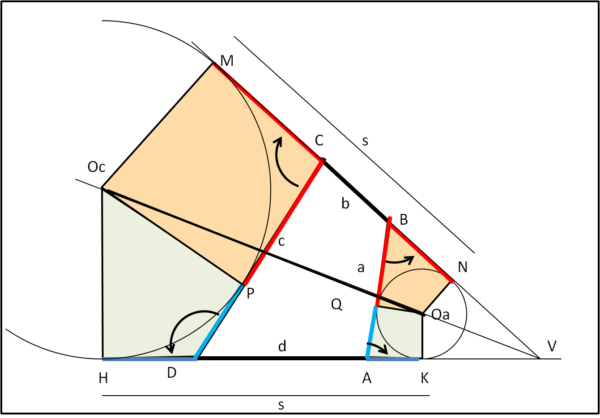
I segmenti rossi e quelli azzurri sono tra loro congruenti (tangenti tracciate da un punto esterno a una circonferenza). Ne segue subito che:
MN = MC + BN + b = PC + QB + b
e, analogamente:
HK = PD + QA + d
Sommando le due espressioni:
MN + HK = PC + PD + b + d + QB + QA
MN + HK = c + b + d + a = p (perimetro quadrilatero di partenza)
Ma...
MN = HK
2MN = 2HK = p
da cui
MN = HK = p/2 = s
I lati MN e HK , congruenti tra loro, sono proprio il semiperimetro del quadrilatero di partenza.
Ribadiamo, perciò, la (1), ossia che la somma delle aree dei quadrilateri (tra loro congruenti) verde e giallo di Fig. 2 è uguale al prodotto tra il semiperimetro del quadrilatero di partenza (s) e la somma dei raggi (ra e rc) delle due circonferenza di centro Oa e Oc.
(C) Possiamo anche concludere che l'area K del quadrilatero di partenza è uguale alla somma delle aree dei quadrilateri verde e giallo di Fig. 2 meno le aree dei quadrilateri rosa e azzurri di Fig. 4. Ma quanto valgono queste ultime aree? ed ecco un ulteriore brillante azione...
Inseriamo la Fig.5.
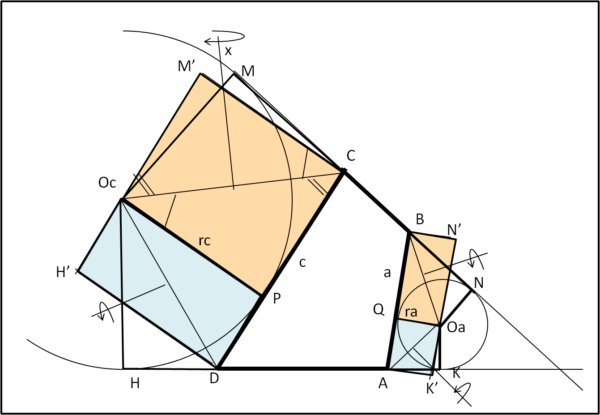
Descriviamo solo il caso del quadrilatero OcMCP (uguale discorso vale, però, per gli altri tre). Dividiamolo a metà con la congiungente OcC. Il triangolo superiore OcMC è congruente con quello inferiore OcCP (tre lati congruenti). Ribaltiamo quello superiore ruotandolo attorno all'asse x. Otteniamo un nuovo quadrilatero OcM'CP. Gli angoli in M' e in P sono retti, gli angoli in C e Oc sono congruenti per costruzione, dato che uguali alla somma di angoli uguali. La loro somma, però, deve essere uguale a 180° (la somma dei quattro angoli di un quadrilatero è 360°, di cui 180° sono relativi alla somma dei due angoli retti). Essendo uguali tra loro, ognuno deve valere 90°. Il nuovo quadrilatero OcM'CP (che ha la stessa area di OcMCP) è, quindi, un rettangolo la cui area è, di conseguenza:
A(OcMCP) = CP rc
Analoga conclusione si trae per il quadrilatero azzurro in basso (OcPHD). La sua area vale:
A(OcPHD) = DP rc
La loro somma è quindi la stessa dell'area del rettangolo di base rc e altezza (CD + DP) = c:
rc CD = rc (CP + DP) = rc c
Passando ai quadrilateri azzurro e rosa della parte di destra, si ottiene, nello stesso modo, che la somma delle aree dei due quadrilateri risulta essere
ra a
L'area K del quadrilatero di partenza vale quindi, ricordando la (1):
K = s(ra + rc) - ra a - rc c = ra(s - a) + rc(s - c)
Per comodità di scrittura indichiamo con sa la differenza (s - a) e con sc la differenza (s - c). Otteniamo:
K = ra sa + rc sc .... (2)
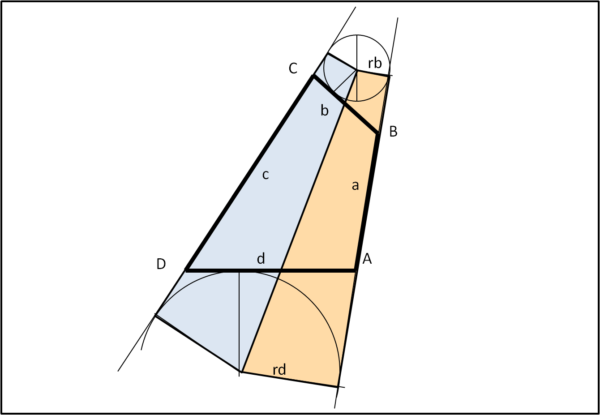
(D) Possiamo adesso lavorare con le circonferenze tangenti ai lati b e d e ripetere tutto il procedimento fatto fino ad ora. Alla fine si ottiene:
K = rb sb + rd sd .... (3)
Inserisco a questo riguardo la Fig. 6 e vi invito a svolgere i calcoli da soli, ripartendo dal punto (A), per controllare che abbiate compreso esattamente la procedura seguita...
La dimostrazione è tutt'altro che finita e occorrono due azioni semplici, ma assai brillanti. Interrompiamo per adesso la faccenda dando tempo di assimilare bene quanto fatto
P.S.: Ovviamente, in attesa della prosecuzione della dimostrazione, siete liberi di agire da soli...





