Oggi, 23 novembre ^(*), è la giornata mondiale dedicata a Fibonacci e ci uniamo alle celebrazioni riproponendo la tesina che la nostra Valentina scrisse nel 2018 per il suo esame di maturità. Nel frattempo la "maghetta" ha conseguito la laurea triennale in matematica e sta proseguendo il suo percorso magistrale. Brava Vale, continua così!

(*) E' stato scelto il 23 novembre perché, usando la notazione statunitense (mese-giorno-anno), questa data si scrive 11/23 e 1,1,2,3 costituiscono i primi termini della successione di Fibonacci.

 

Questo articolo è stato inserito in

"Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo e in "Antichi Greci, che passione!"

 

Spesso è sorprendente come certi concetti matematici apparentemente astratti abbiano così tante manifestazioni nel mondo reale! Tra i più sorprendenti c'è senz'altro il numero aureo, al quale ho dedicato la tesina del mio esame di maturità, concentrandomi sulle applicazioni in campo artistico, dopo averne spiegato a grandi linee le caratteristiche matematiche e geometriche.

Buona lettura!

 

A SPASSO TRA MATEMATICA E ARTE IN COMPAGNIA DEL NUMERO AUREO

“La geometria possiede due grandi tesori: uno è il teorema di Pitagora, l’altro è la divisione di una linea secondo il rapporto estremo e medio. Possiamo paragonare il primo ad una certa quantità d’oro, e definire il secondo una pietra preziosa”  (Giovanni Keplero 1571-1630)

 

1. INTRODUZIONE

Chi era Leonardo Pisano Bigollo Bonacci (Pisa 1175 – 1235 circa)? Più noto con lo pseudonimo di FIBONACCI (ovvero filius Bonacci), non ha scoperto niente di estremamente utile per l’uomo, né ha contribuito alla conoscenza di ciò che ci circonda, ma è considerato uno dei più grandi matematici di tutti i tempi e ha il grande merito di aver fatto conoscere in Europa i numeri indo-arabici, che utilizziamo oggi. Era figlio di un mercante e, accompagnando suo padre nei suoi viaggi di lavoro, ebbe modo di frequentare la scuola di conto di un maestro musulmano. Nel suo famoso “Liber Abaci” (pubblicato nel 1202) egli afferma “le nove cifre degli indiani sono queste 9,8,7,6,5,4,3,2,1. Con queste nove cifre e con questo simbolo 0, che in arabo si chiama Zephir, si può scrivere qualsiasi numero”.

Ma non è tutto… in un’epoca “buia” per l’intelletto umano come quella in cui lui ha vissuto, la sua mente era tanto illuminata da riuscire a cogliere una straordinaria regolarità in una serie di numeri costruita molto semplicemente:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377………………

Che legame hanno tra loro? Facilissimo: ognuno è la somma dei due precedenti.

1+1=2, 1+2=3, 2+3=5, 3+5=8 e così via…

Fin qui sembra solo un gioco da bambini, e non si comprende il motivo della grande notorietà di questa successione. Per farlo, è necessario fare un passo indietro nel tempo, anzi… molti passi indietro ma, prima di iniziare il viaggio, è bene soffermarci su alcuni concetti geometrici e matematici.

 

2. COS'E' LA SEZIONE AUREA

In matematica, due quantità a e b si dicono in rapporto aureo se la maggiore è medio proporzionale tra la minore e la somma delle due

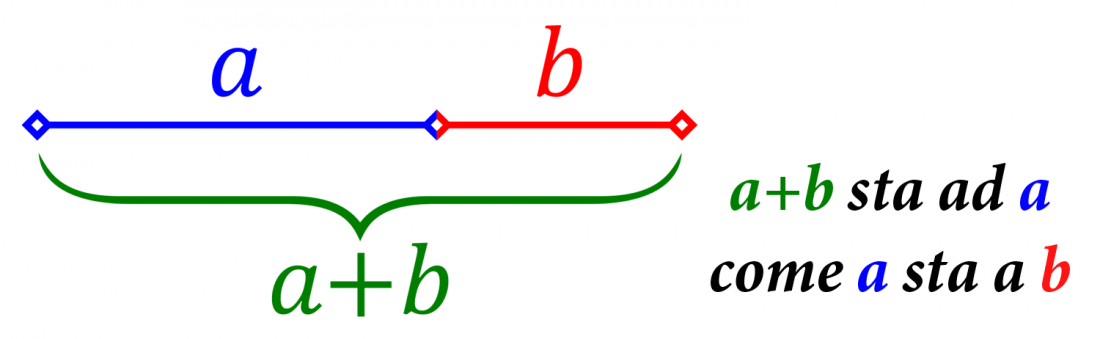
Se a >b, in simboli si scrive:

Il rapporto tra le due grandezze viene detto SEZIONE AUREA, si indica con la lettera ϕ (phi) e, se la sostituiamo al rapporto a/b:

Moltiplicando per  ϕ  e riordinando i termini, otteniamo l’equazione

La cui unica soluzione positiva è

La sezione aurea ϕ è un numero irrazionale, ovvero un numero che non può essere espresso come intero o come quoziente di interi. È, inoltre, l’unico numero reale positivo il cui reciproco è dato da se stesso meno 1, vale a dire

da cui segue che

ovvero ϕ e il suo reciproco hanno la stessa parte decimale

 

3. COME COSTRUIRE LA SEZIONE AUREA

Come trovare due segmenti che stanno in rapporto aureo? La costruzione è semplice: bastano una riga e un compasso.

Con essi si costruisca un quadrato di lato qualunque e, puntando il compasso nel punto medio di uno dei lati si tracci un arco di cerchio che parta da un estremo del lato opposto e incontri il prolungamento del lato in cui si è puntato il compasso: abbiamo tutti i riferimenti per costruire un rettangolo con base e altezza in rapporto aureo.

Per esempio, partendo da un quadrato di lato 1

 

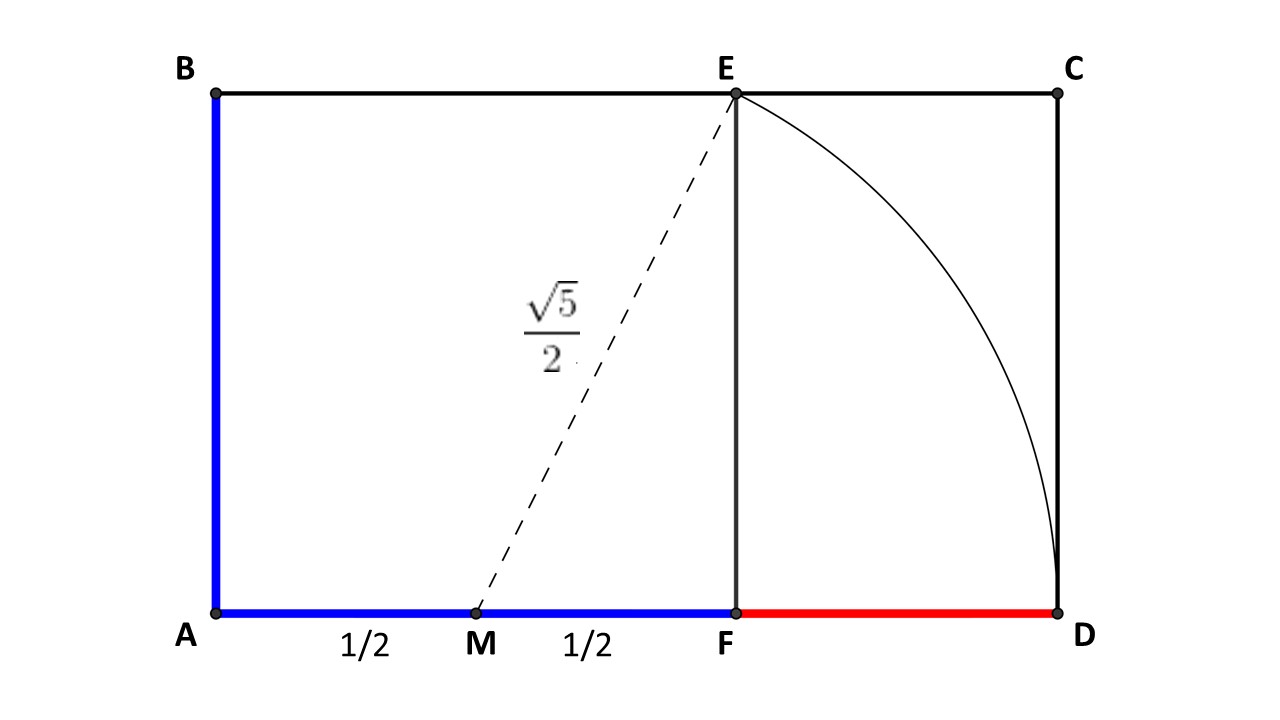
La base AD e l’altezza CD del rettangolo ABCD sono in rapporto aureo!

Ogni rettangolo la cui base e altezza sono in rapporto aureo tra loro, viene detto rettangolo aureo, dunque ABCD è aureo, ma anche CDEF lo è, infatti

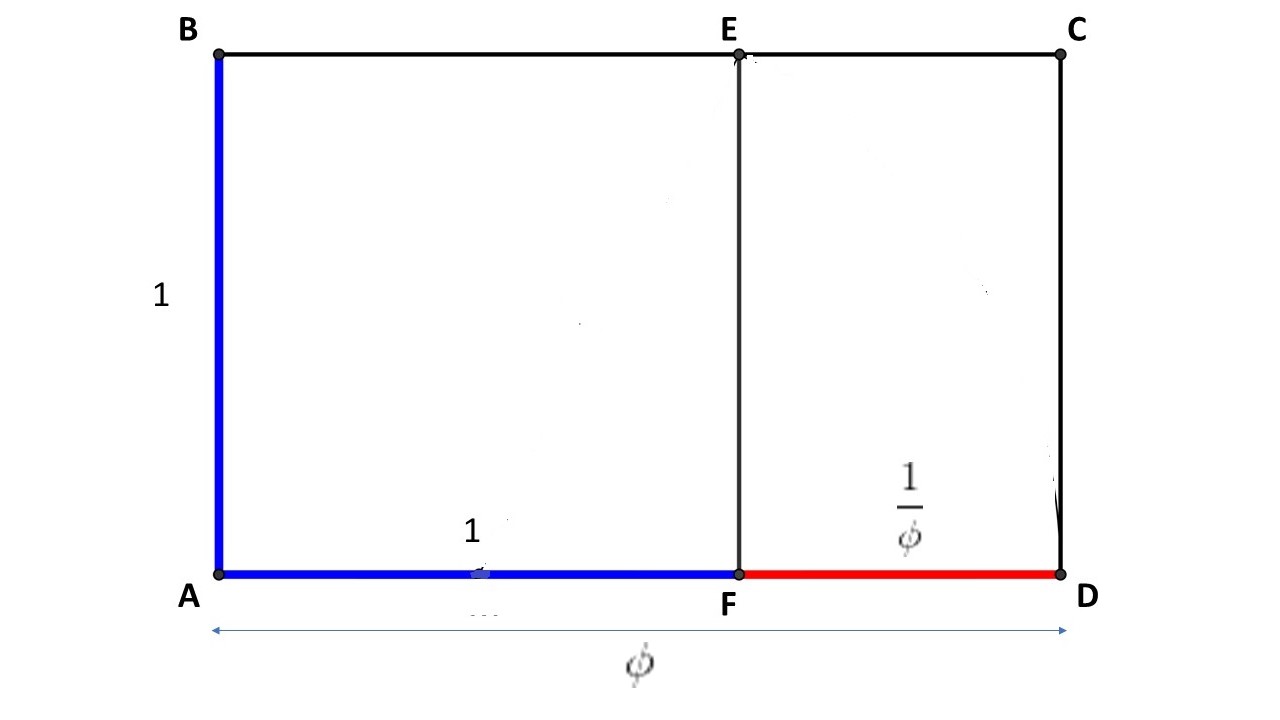
E questo è solo l’inizio di una serie infinita di rettangoli aurei

 

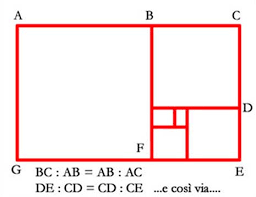
4. LA SPIRALE DI FIBONACCI-LUCAS

A questo punto, tracciando un quarto di cerchio in ogni quadrato, compare una tanto strana quanto armoniosa curva: la SPIRALE DI FIBONACCI-LUCAS

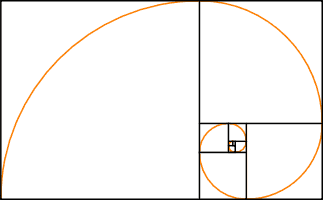
Il fatto che il nome di Fibonacci sia associato a questa spirale, ci fa intuire che essa abbia qualcosa a che fare con la successione di cui abbiamo parlato all’inizio. Affronteremo l’argomento tra poco; intanto ci chiediamo se sia legata alla sezione aurea.

La risposta non può che essere affermativa! Non è un caso, infatti, che essa appaia anche in altre figure legate alla sezione aurea:

nel TRIANGOLO AUREO (triangolo isoscele avente il lato in rapporto aureo con la base)

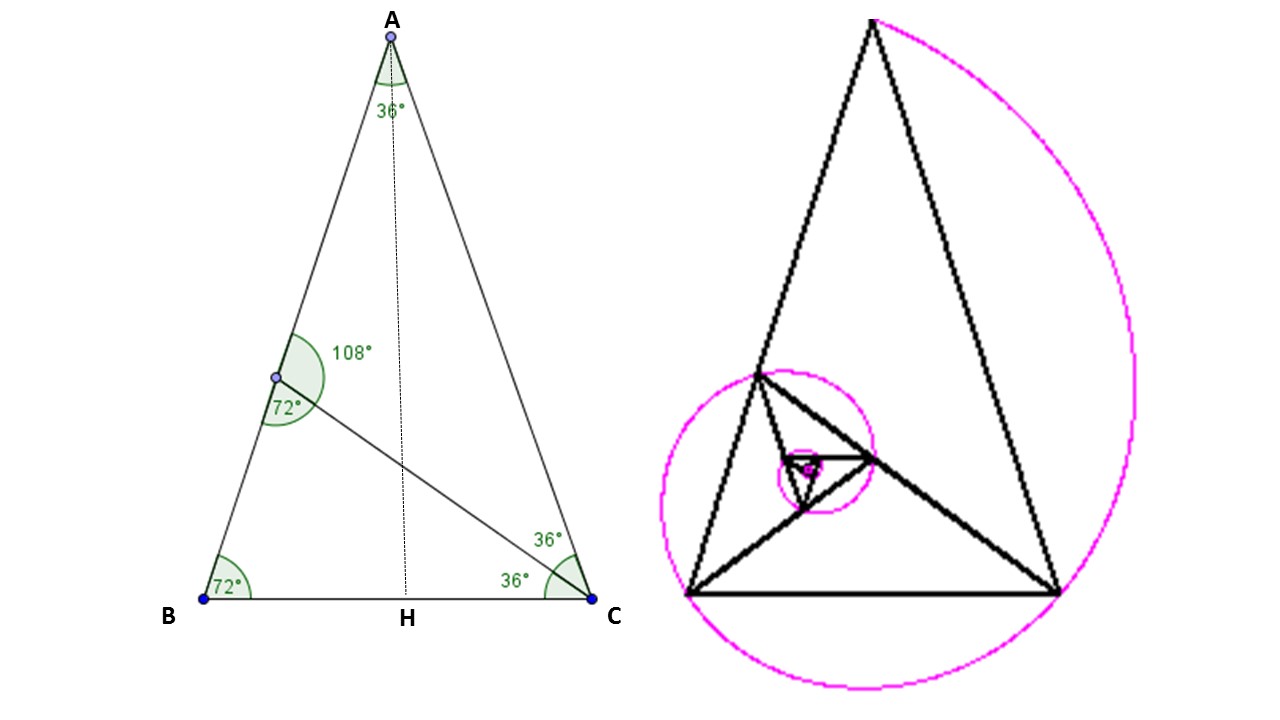
2α = 72°

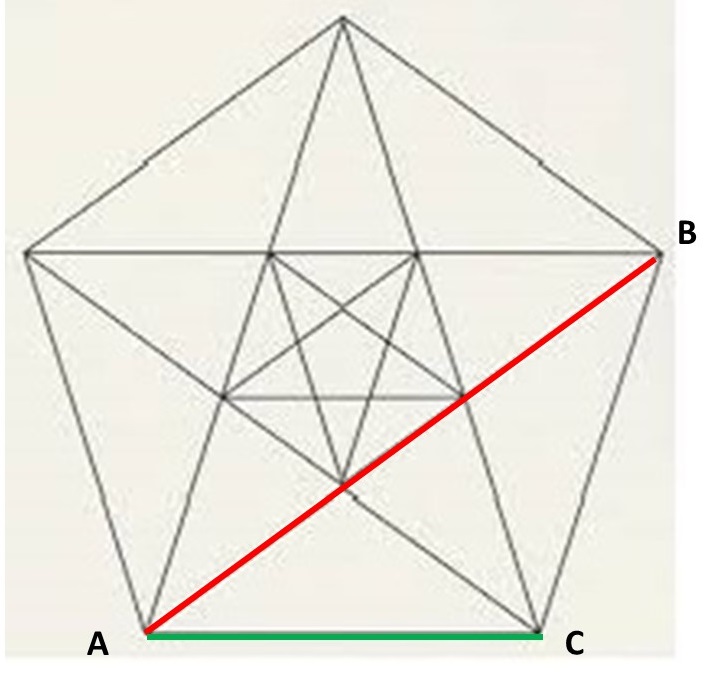
e nel PENTAGONO REGOLARE, che incorpora molti triangoli aurei, vediamo perché…

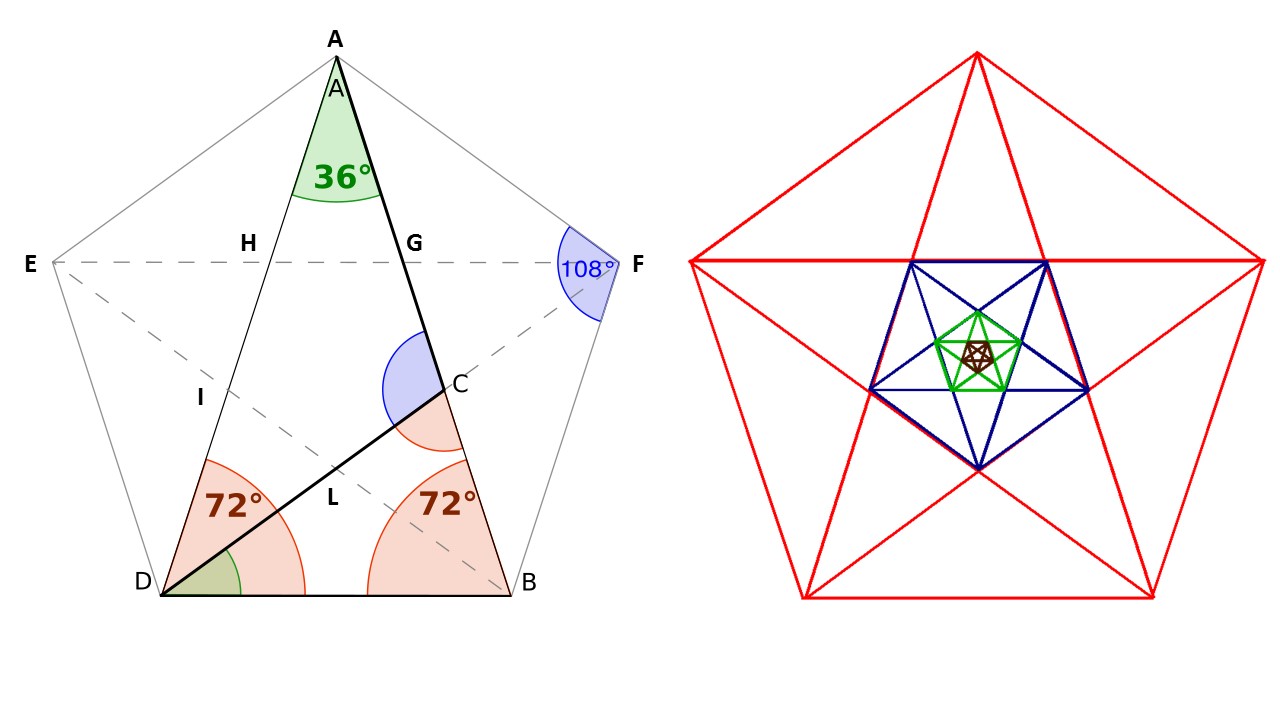
ABD è un triangolo aureo, infatti:

quindi anche il triangolo AGH è aureo, in quanto simile (ha tutti gli angoli uguali) a ABD. Lo stesso dicasi per CFG che è simile a DEF, e così via per tutti gli altri.

Possiamo, inoltre, notare che il pentagono CGHIL ha tutti gli angoli di 108°, quindi anch’esso è aureo e, tracciando le sue diagonali, otteniamo altri triangoli aurei e un altro pentagono regolare. È evidente che possiamo continuare questo procedimento indefinitamente.

E, disponendo una serie di pentagoni regolari in modo che il vertice di ciascuno divida il lato di un altro secondo la sezione aurea, qualcosa di molto simile alla spirale di Fibonacci è pronto a fare la sua comparsa!

 

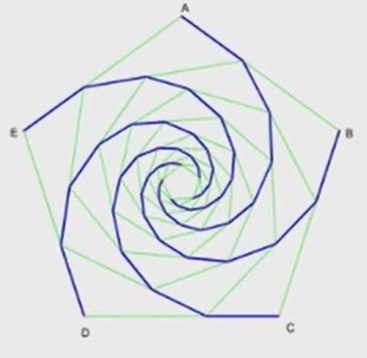
5. IL LEGAME TRA LA SEZIONE AUREA E LA SUCCESSIONE DI FIBONACCI

Tutto ciò non può essere frutto del caso né della magia, infatti c’è un solido legame matematico tra la sezione aurea e la spirale di Fibonacci. Vediamolo…

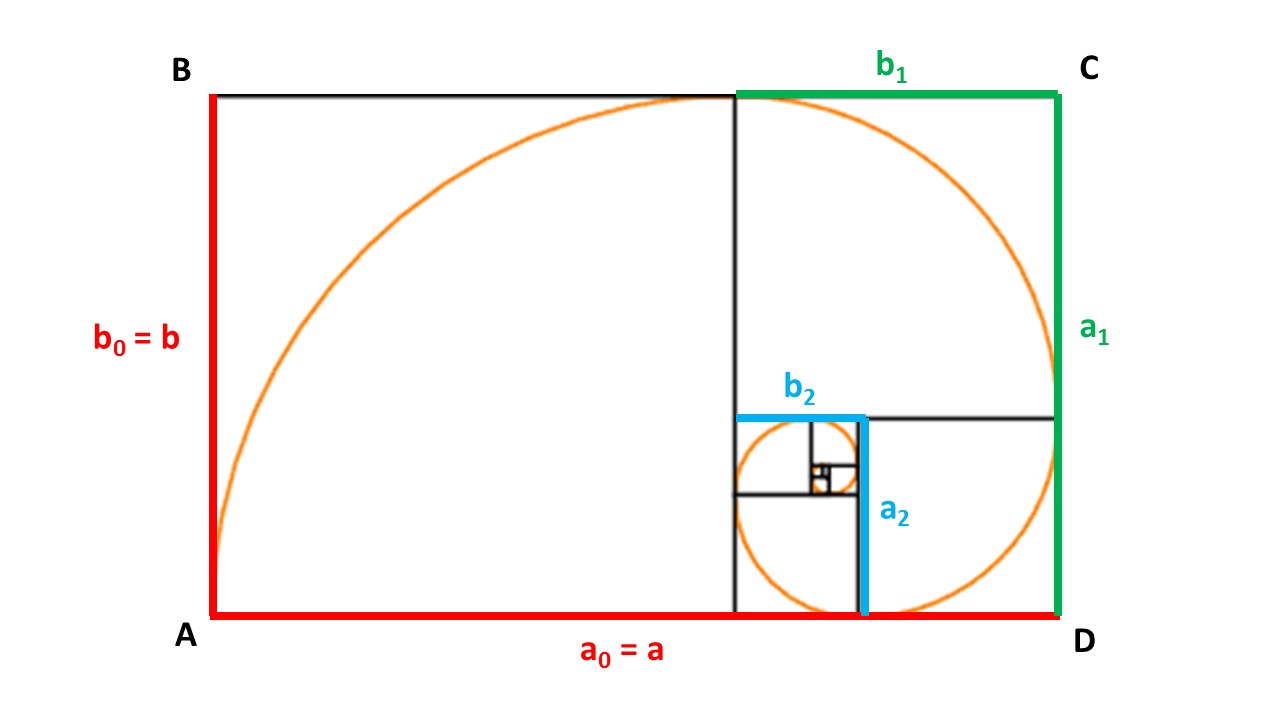
Sia ABCD un rettangolo aureo con lati a₀ = a e b₀ = b (a>b). Per questo rettangolo e per tutti i rettangoli aurei inscritti, varrà la seguente relazione:

Dove b_i e a_i sono rispettivamente l’altezza e la base dell’i-esimo rettangolo.

Proviamo a calcolare ogni altezza b_i in funzione del lato a:

I numeri cerchiati in rosso fanno parte della successione di Fibonacci, quelli in verde formano la successione di Lucas che è imparentata con quella di Fibonacci: inizia con 1 e 3, dopodiché ogni numero è la somma dei due che lo precedono.

 

6. L’ORIGINE DELLA SUCCESSIONE DI FIBONACCI

A questo punto, chiarito il legame tra la sezione aurea e la serie di Fibonacci, resta da capire come una serie numerica così particolare sia venuta in mente al figlio di un mercante, vissuto nel XIII secolo. Come molte altre importanti scoperte nella storia del pensiero scientifico, l’occasione arriva per puro caso: questa volta è arrivata a Pisa nel 1223… Leonardo Pisano figlio di Bonacci, per sua e nostra fortuna, si trova al posto giusto nel momento giusto. Durante un torneo tra abacisti e algoritmisti viene proposto il seguente quesito:

“un tale mise una coppia di conigli in un luogo completamente circondato da un muro, per scoprire quante coppie di conigli discendessero da questa in un anno; per natura le coppie di conigli generano ogni mese un’altra coppia e cominciano a procreare a partire dal secondo mese dalla nascita”.

La conoscenza dei numeri indo-arabici fu fondamentale per Fibonacci per arrivare velocemente alla soluzione. Tanto velocemente che qualcuno sospettò che il torneo fosse truccato.

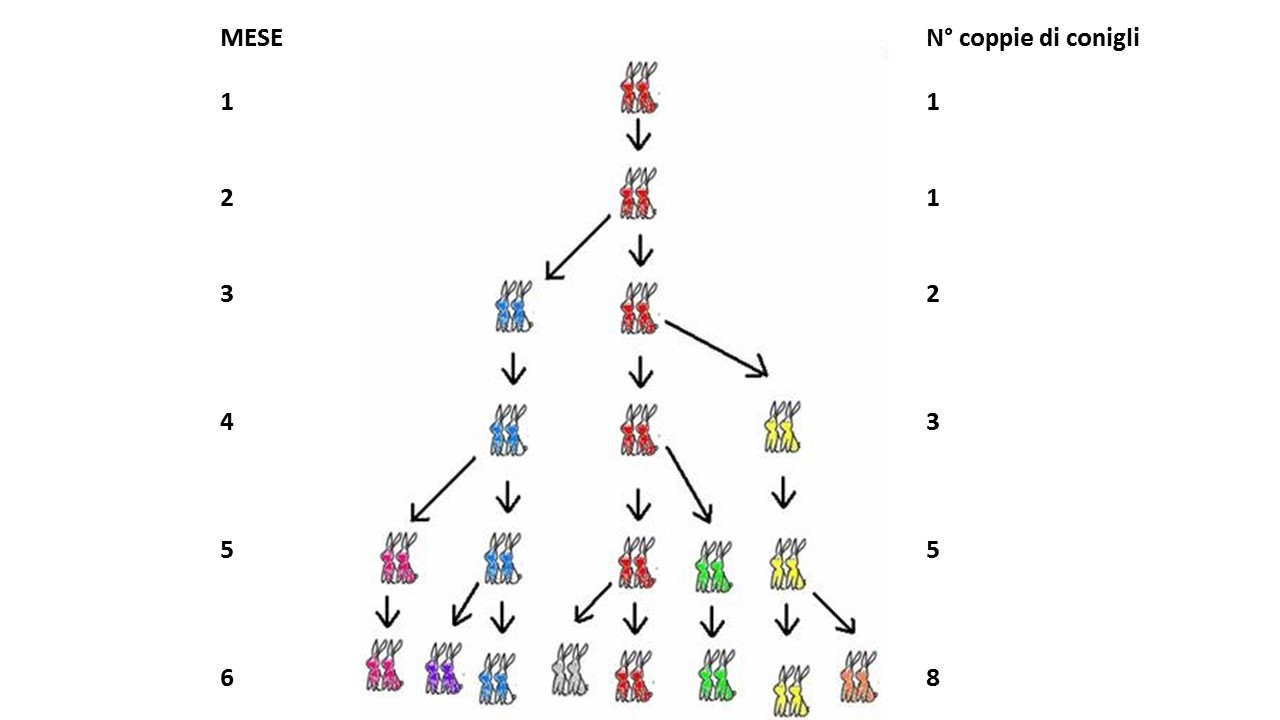
Le coppie di conigli (ipotizzando che rimangano tutti in vita) aumentano secondo la serie di Fibonacci. Perché?

La risposta è semplice: ad un dato mese, i conigli fertili nel recinto sono tutti i conigli nati almeno un mese prima, ovvero tutti i conigli presenti nel recinto un mese prima. Allora se indichiamo con F_n il numero di conigli presenti al mese n e con F_n-1 il numero di quelli presenti il mese precedente, al mese n+1 saranno nati esattamente F_n-1 nuovi conigli e dunque nel recinto ci saranno F_n + F_n-1 conigli, cioè:

F_n+1 = F_n + F_n-1

il numero dei conigli ad un dato mese è la somma del numero dei conigli presenti nei due mesi precedenti.

 

7. RAPPRESENTAZIONE GEOMETRICA DEI NUMERI DI FIBONACCI

Come ϕ, anche i numeri di Fibonacci hanno una rappresentazione geometrica interessante e facile da realizzare: cominciando con un quadrato di lato 1, si può generare una successione di quadrati i cui lati sono numeri di Fibonacci successivi. Questo procedimento si può ripetere indefinitamente.

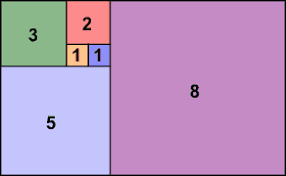
A questo punto, tracciando un quarto di cerchio in ogni quadrato, otteniamo una spirale che si avvicina molto a quella aurea:

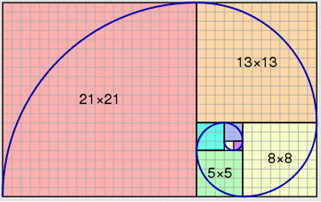
Sarà un caso? Ovviamente no e possiamo dimostrarlo facendo i rapporti tra a lunghezza di lati consecutivi, ovvero:

Non ci vuole molto perché i rapporti inizino visibilmente a convergere verso 1,618 che costituisce una buona approssimazione del valore della sezione aurea

E, continuando a calcolare i rapporti di numeri di Fibonacci consecutivi, il valore si avvicinerà sempre di più a ϕ, quindi possiamo dedurne che

Quindi i numeri di Fibonacci ci danno una stima della Sezione Aurea!

In termini matematici, significa che la serie di Fibonacci è una sequenza di razionali che converge al numero irrazionale ϕ. E’ per questo motivo che, quando prendiamo i quadrati di Fibonacci, compare la spirale legata a ϕ. Infatti i rettangoli inscritti sono “quasi” rettangoli aurei, avendo i lati in un rapporto molto vicino alla sezione aurea.

 

8. UN PO’ DI STORIA

 

A questo punto siamo pronti per compiere quel viaggio nel tempo a cui si accennava all’inizio: programmiamo la macchina del tempo per il VI secolo a.C. per incontrare Pitagora e i seguaci della sua Scuola. Fu, infatti, la Sezione Aurea il primo numero irrazionale in cui essi si imbatterono e, convinti com’erano che tutte le forme geometriche potessero essere descritte in termini di numeri interi, fu per loro una beffa scoprire, che proprio il loro simbolo (il pentagono stellato) conteneva un rapporto che non poteva essere espresso come frazione di numeri interi.

 

 

 

        

 

 

Dovettero passare altri tre secoli, però, per avere una definizione rigorosa di quello che, in seguito, avrebbe preso il nome di “rapporto aureo”. Ci pensò Euclide nel III sec. a.C., che scrisse: “Si può dire che una linea retta sia stata divisa secondo la proporzione estrema media quando l’intera linea sta alla parte maggiore così come la maggiore sta alla minore”.

 

 

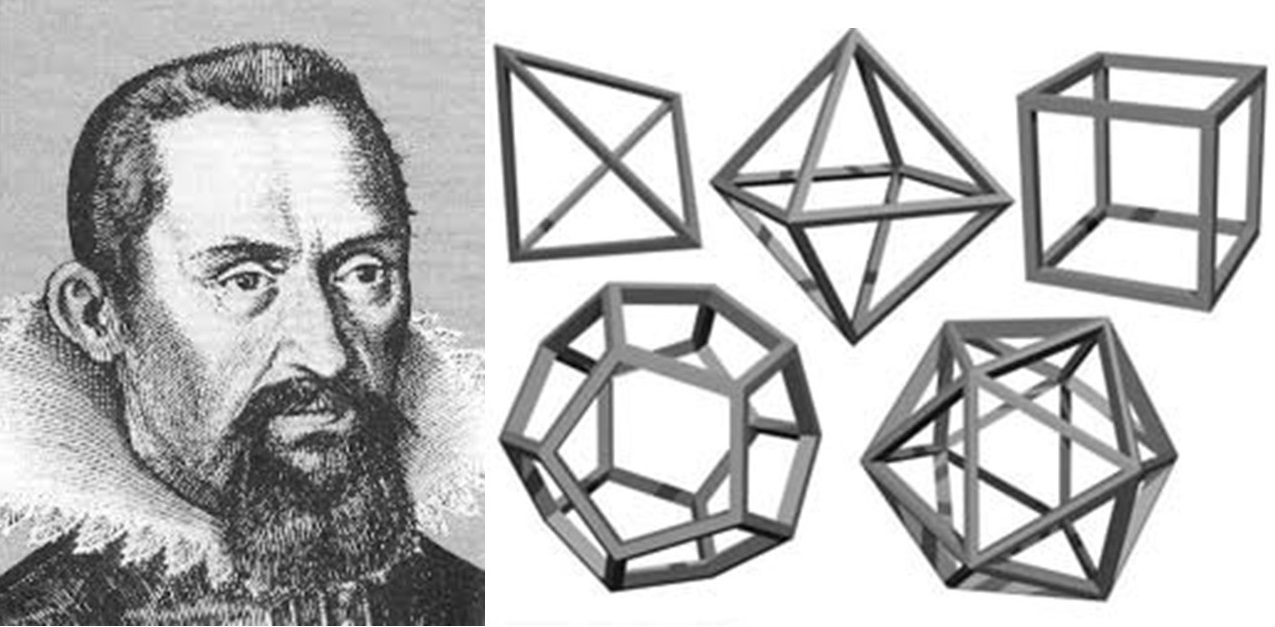
E ne dovettero passare altri diciannove prima che Keplero, alla ricerca dello strumento matematico di cui si era servito l’Onnipotente per progettare l’universo, agli albori del XVII secolo, scoprisse il rapporto tra ϕ e i numeri di Fibonacci. Egli, infatti, aveva ideato un modello cosmologico in cui ogni pianeta si muoveva in una sfera circoscritta o inscritta in un poliedro platonico (cubo, dodecaedro, tetraedo, icosaedro, ottaedro) e osservò che essi “non si possono formare senza questa proporzione che gli odierni studiosi di geometria chiamano divina. Questa è congegnata in modo tale che i due termini minori di una serie nascente presi insieme formano il terzo, e gli ultimi due addizionati il termine successivo, e così via indefinitamente… credo che da questa proporzione geometrica abbia preso spunto il Creatore quando introdusse la produzione del simile dal simile che prosegue anch’essa indefinitamente”.

 

9. LA SEZIONE AUREA NELLA STORIA DELL’ARTE

Chi ha il merito di avere procurato notorietà al rapporto aureo fra i non matematici è Fra’ Luca Pacioli che, nel 1509, nel suo “De divina proportione” (illustrato da Leonardo da Vinci) tradusse dal latino il trattato sui poliedri di Piero della Francesca, il più prolifico tra gli artisti rinascimentali per quanto riguarda la matematica. Egli, infatti, oltre ad opere pittoriche di mirabile bellezza estetica, ci ha lasciato tre opere matematiche (altre sono andate perdute), scritte quando ormai l’età avanzata non gli consentiva più di dipingere: “La prospettiva pittorica”, il “Breve libro sui cinque solidi regolari” e il “Trattato d’abaco”.

 

 

Nonostante l’accusa di plagio mossagli dal Vasari per non avere dato il giusto risalto alla sua fonte, a Fra’ Luca Pacioli va riconosciuto il grande merito di aver dato impulso all’ampia circolazione delle idee di Piero della Francesca e dei suoi procedimenti matematici che, in assenza di tale opera, avrebbero rischiato di rimanere sconosciuti. È grazie a Pacioli, infatti, che la “proporzione estrema media” acquisisce il più affascinante e accattivante nome di “divina proporzione” e diventa familiare anche a pittori, scultori e architetti.

Ma siamo già nel XVI secolo, pertanto questa affermazione appare in contrasto con la presunta presenza delle divine proporzioni in moltissime opere d’arte, a partire dall’antichità. È sufficiente, infatti, digitare “arte e numero aureo” su un qualunque motore di ricerca, per trovare molte immagini di opere che, ad una prima analisi, sembrano davvero essere piene di proporzioni auree. Ma è davvero così? Secondo Mario Livio, astrofisico di fama internazionale che ha voluto approfondire la questione, non è tutto aureo ciò che luccica! Infatti se, da un lato, è certamente facile individuare rettangoli aurei in molte opere d’arte, dall’altro le incertezze sulle misure rendono spesso tale interpretazione un mero gioco di prestigio numerico.

Tra le opere più illustri sospettate di essere state progettate intorno a proporzioni auree, si annoverano capolavori come il Partenone, il tempio della Cariatidi, la Venere di Milo, Monna Lisa e altre famose opere di Leonardo da Vinci. E, osservando queste immagini, sembra proprio che sia così:

Ma, se si riflette sul fatto che basta variare di pochissimo le misure di questi rettangoli per fare saltare le loro proporzioni auree, è evidente che, sulla loro effettiva presenza, si può dire tutto e il contrario di tutto.

Analizziamo, per esempio, queste tre Madonne che, per puro caso, si trovano oggi esposte nella stessa sala della Galleria degli Uffizi

 In molti libri si afferma che sia i dipinti nella loro interezza che i gruppi delle figure centrali siano perfettamente inscrivibili in rettangoli aurei.

In realtà, a parte le incertezze di misura dovute alle linee piuttosto spesse, i rapporti altezza/larghezza sono rispettivamente pari a 1,59 – 1,55 – 1,73 metri. Valori solo vicini, quindi a ϕ. Oltretutto, a parte l’inconscia attrazione estetica che può avere esercitato il rapporto aureo nei confronti degli autori, non c’è motivo storico per ritenere che esso sia stato usato in modo intenzionale, tenendo anche conto del fatto che tali opere precedono di oltre due secoli la pubblicazione dell’opera di Fra’ Pacioli.

Più credibile è l’ipotesi circa la presenza di rettangoli aurei in alcune celebri opere di Leonardo da Vinci, vista la sua frequentazione con Luca Pacioli (che nel 1496 fu invitato alla corte di Ludovico il Moro a Milano, probabilmente su sollecitazione dello stesso Leonardo, affinché insegnasse la dottrina dei numeri), ma certezze non ce ne sono in quanto l’analisi delle opere non toglie ogni dubbio; né possiamo dimenticare il fatto che molte opere sono precedenti all’incontro tra Leonardo e Pacioli.

 

 

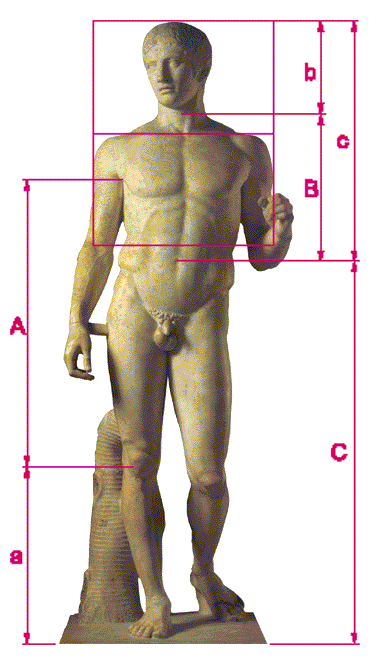
 È, tuttavia, innegabile che la particolare passione degli antichi greci per l’armonia geometrica si sia concretizzata nella realizzazione di opere la cui bellezza “nasce dall’esatta proporzione non degli elementi, ma di tutte le parti tra di loro”, come affermava Policleto, cultore della matematica pitagorica, vissuto nel V secolo a.C., autore del celebre “Canone”, il trattato che elencava le norme e le proporzioni da seguire per riprodurre l’anatomia umana nel marmo e che ha costituito un punto di riferimento fondamentale per molte generazioni future di scultori e bronzisti. La sua opera più celebre, il Doriforo, costituisce la sintesi dei suoi insegnamenti, oltre ad essere un lampante esempio di utilizzo delle proporzioni auree.

Quindi, se da un lato è prudente e condivisibile non voler far diventare la sezione aurea il prezzemolo dell’arte classica, dall’altro sarebbe ingiusto pensare che non vi sia presente o lo sia saltuariamente e per puro caso. E se le incertezze di misura possono sollevare ragionevoli dubbi, non si può ignorare che la ricerca di armonia geometrica costituisca il faro dell’arte greca e si concretizzi in opere dalle proporzioni che, anche quando non sono perfettamente auree, certamente vi si avvicinano molto.

Per avere la certezza di un uso consapevole e non approssimativo del rapporto aureo nelle opere d’arte, è necessario arrivare al termine del XIX secolo. Ma, contrariamente a quanto molti pensano, non è detto che sia Georges Seurat il primo ad adottarlo. Infatti la sua “La Parade du cirque” che viene portata come esempio in tal senso, presenta delle interruzioni della dimensione orizzontale che si avvicinano soltanto al rapporto aureo, mentre non ve n’è traccia nella sua dimensione verticale.

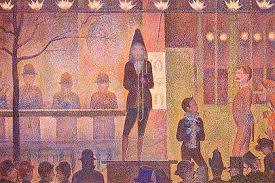
Il primo importante artista a impiegare ϕ nelle sue opere fu probabilmente Paul Sérusier (1864-1927) che, tuttavia, sembra avere avuto, nei confronti del rapporto aureo un interesse più filosofico che pratico. Possiamo, infatti, trovare una storia di questo rapporto e del presunto legame tra esso e la piramide di Cheope e l’arte greca nel manuale di pittura da pubblicato dal titolo “L’ABC de la peinture”. Non tralasciò, comunque, di utilizzare la divina proporzione in alcune opere.

L’eredità di Sérusier fu raccolta dai cubisti il cui stile, basato sulla scomposizione formale delle figure per trasferire sul piano la struttura degli oggetti tridimensionali, ben si prestava a valorizzare concetti geometrici come quello di rapporto aureo. L’interesse dei cubisti nei suoi confronti, alimentato dal desiderio di approfondire i legami tra scienza, arte e filosofia, si manifestò in modo plateale nel titolo stesso dato ad una mostra che ebbe luogo a Parigi nell’ottobre del 1912: “Section d’Or”. In realtà nessuna delle opere presenti alla mostra utilizzava la sezione aurea, ma in seguito essa fu davvero utilizzata da artisti come lo spagnolo Juan Gris (1887 – 1927) e lo scultore lituano Jacques Lipchitz (1891 -1973). Tra l’altro, essi collaborarono anche alla realizzazione di una scultura – Arlequin - basata sul triangolo aureo.

Juan Gris spesso procede secondo un sistema di rettangoli o triangoli legati da fattori di proporzionalità. Ne Il lavabo la composizione è articolata su una rete di rettangoli aurei.

Anche Jaques Villon (1875 - 1963) si preoccupa di dare una sottostante struttura geometrica alle sue opere e poi interviene spostando e spezzando leggermente le linee.

Questo metodo è evidente nella sua opera “Soldati in marcia”  in cui traspare l'impianto geometrico costituito da linee diagonali;  le più significative tra queste si incontrano e formano angoli di 36° permettendo quindi di considerare triangoli isosceli in cui  lato e lato di base stanno  tra loro secondo il rapporto aureo. Le armi dei soldati si allineano secondo queste inclinazioni.

Tra gli artisti italiani che utilizzarono le proporzioni auree nelle proprie opere, troviamo il futurista Gino Severini (1883 – 1966) il cui obiettivo era “creare, per mezzo della pittura, un oggetto con la stessa perfezione artigianale con cui un maestro ebanista crea un mobile”. Un mirabile esempio di tale ricerca di perfezione geometrica, soddisfatta ricorrendo al rapporto aureo, lo troviamo nel dipinto “La Maternità”

Uno dei maggiori sostenitori dell'applicazione della sezione aurea all’arte e all’architettura fu Charles-Edouard Jeanneret, meglio conosciuto come Le Corbusier (1887 – 1965)

La ricerca di Le Corbusier  di una proporzione standardizzata trovò la sua massima espressione nell’introduzione di un nuovo sistema proporzionale chiamato “Modulor”, consistente in un insieme di misure per fornire alla scala umana una misura di armonia, universalmente applicabile all'architettura e alla meccanica, idea simile a quella di Protagora (filosofo greco del V secolo a.C.) secondo il quale l’uomo è la misura di tutte le cose.

In pratica, il Modulor rappresenta un uomo alto circa 183cm e con un braccio alzato (altezza totale = 226 cm)inserito in un quadrato.

• il rapporto tra la statura dell'uomo (183cm) e la distanza dall'ombelico al suolo (113cm) è pari a Φ
• l'altezza totale (226cm), compreso il braccio alzato, è divisa dal livello del polso dell'altro braccio secondo il rapporto aureo (140cm e 86cm)
• i due rapporti 113/70 e 140/86 erano ulteriormente suddivisi in dimensioni minori secondo la serie di Fibonacci (essendo ciascun numero uguale alla somma dei precedenti

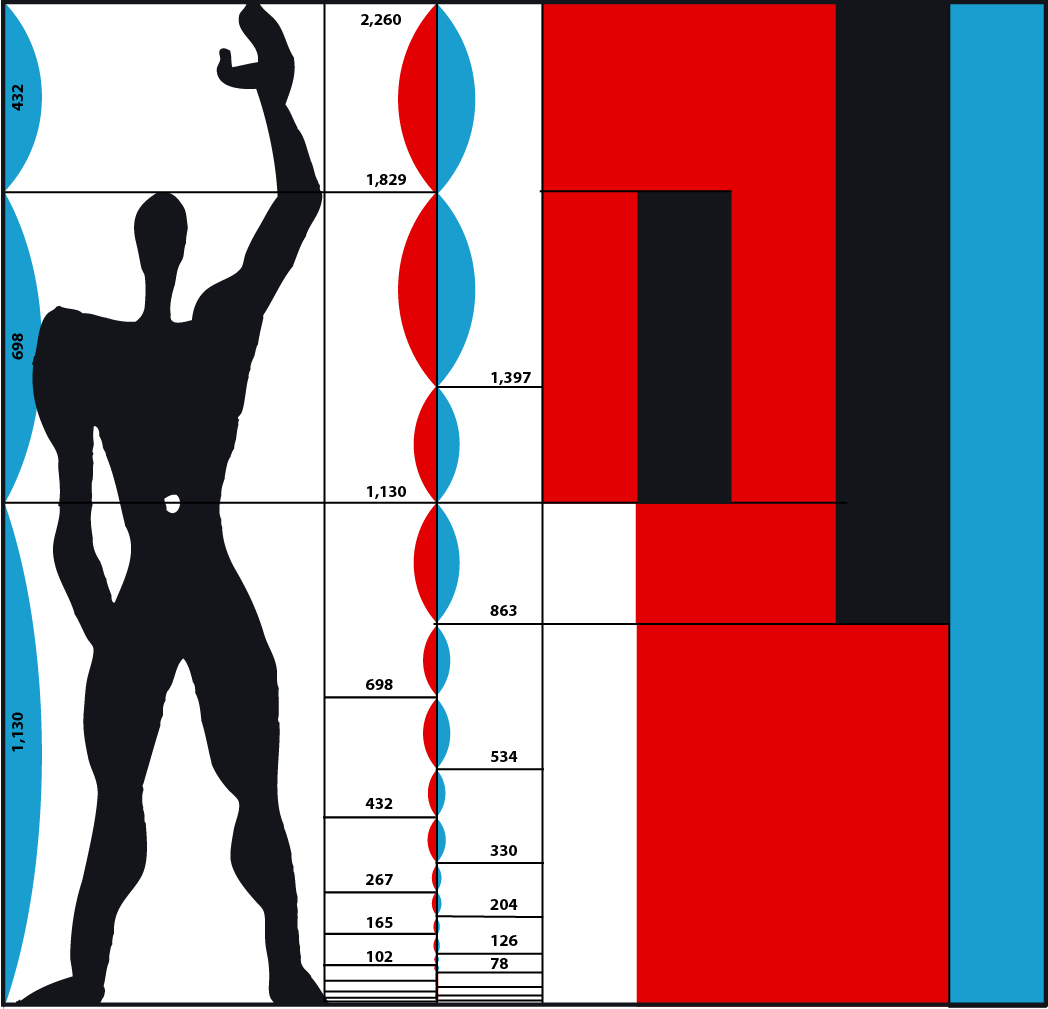
Nella versione finale del Modulor furono quindi introdotte due scale dimensionali basate sulla successione di Fibonacci, le 'serie rossa e blu'.  Secondo Le Corbusier, questo Modulor apportava   dimensioni armoniose a tutto, dagli armadietti alle maniglie delle porte, dai palazzi agli spazi urbani. Le proporzioni del Modulor vennero utilizzate in molti suoi progetti, per esempio quello di Villa Stein a Garches (Francia).

Chiudiamo questa carrellata di opere d’arte con questa “Ultima cena” del pittore surrealista Salvador Dalì, racchiusa in un rettangolo aureo, con il grande dodecaedro che la sovrasta e che richiama, con le sue facce pentagonali, la sezione aurea.

Armonia, bellezza, regolarità e un pizzico di mistero rendono così affascinante il numero aureo e tutto ciò che gli ruota intorno, soprattutto per la sua propensione a comparire quando meno ce lo si aspetta. E l’universo si diverte spesso ad usarlo, dall’infinitamente piccolo all’infinitamente grande…

“Quella del mistero è la più straordinaria esperienza che ci sia dato di vivere. E’ l’emozione fondamentale situata al centro della vera arte e della vera scienza”

(Albert Einstein)

 

E di mistero i numeri ne hanno da vendere, è per questo che sono così affascinata dai loro “giochi” che sembrano uscire dal cappello di un prestigiatore!

Infatti mi diverto a cercare delle regolarità in certe loro relazioni e, quando ne trovo una, spero di essere stata la prima ad essersene accorta… di solito, purtroppo, non è così: spesso devo prendere atto che qualcuno ha già intuito e dimostrato una certa relazione secoli prima di me.

Come quando mi sono accorta che la somma dei primi n numeri interi elevati al cubo è uguale al quadrato della loro somma… peccato che ci avesse già pensato un certo Nicomaco di Gerasa, matematico e pensatore greco vissuto a cavallo tra il I e II secolo d.C.!

Comunque, che siano o meno originali, certi giochini sono estremanente divertenti e non mi stancano mai.

Un numero particolarmente interessante e ricco di sorprese è l’undici, infatti ci sono vari modi per capire al volo se un numero, anche molto grande, è divisibile per esso.

E che dire del fatto che, se prendo un numero qualunque, lo inverto e sottraggo uno dei numeri dall’altro, ottengo sempre un multiplo di 9? Provare per credere…

Ancora più sorprendente la relazione che ho trovato nell’ambito del Triangolo di Tartaglia, per trovare un termine successivo ad uno dato, senza costruire tutto il triangolo. E questa potrebbe essere originale… per ora, almeno, non sono riuscita a trovarne traccia cercando in internet, speriamo che sia la volta buona!

Ma in matematica, si sa, non basta intuire una relazione e provare che essa è valida su un certo insieme di numeri: per essere certi che abbia un valore universale è necessario darne una dimostrazione di carattere generale. Il che può non essere semplice, specialmente se richiede conoscenze di livello universitario.

Ma questa è un'altra storia che spero di raccontarvi un'altra volta...

Valentina, 4 luglio 2018

                                 

************************************************************************************

Bibliografia

• Mario Livio “La sezione Aurea – Storia di un numero e di un mistero che dura da tremila anni” ed. BUR Rizzoli
• Cricco Di Teodoro “Il Cricco Di Teodoro Itinerario nell’arte” ed. Zanichelli - volumi 3,4 e 5

 

Sitografia

• Young Doctors for Science https://www.youtube.com/watch?v=abagpn8ROOo
• http://www.infinitoteatrodelcosmo.it/2016/06/20/fibonacci-e-luniverso/
• https://www.studentville.it/appunti/mappa-concettuale-canone-di-policleto/
• http://online.scuola.zanichelli.it/sammaronedisegno/files/2010/03/Zanichelli_Sammarone_Sezione_Aurea.pdf