Questo articolo è inserito in Cinematica

 

Potrebbe sembrare che, rispetto alla dinamica, la cinematica sia una parte della meccanica decisamente meno importante. Eppure, è bastata per far compiere un balzo enorme alla Scienza. Ovviamente, con l'aggiunta della mente di Galileo Galilei...

Un esempio estremamente interessante è, infatti, il moto sul piano inclinato. Esso ha permesso a Galileo Galilei di "rallentare" un corpo in caduta libera riuscendo a rendere un esperimento praticamente impossibile (caduta di un grave) misurabile con gli orologi del suo tempo. Aprendo, in tal modo, la porta a Newton.

Disegniamo la ben nota Fig. 1 dove è rappresentato un piano, inclinato di un angolo a rispetto al piano orizzontale.

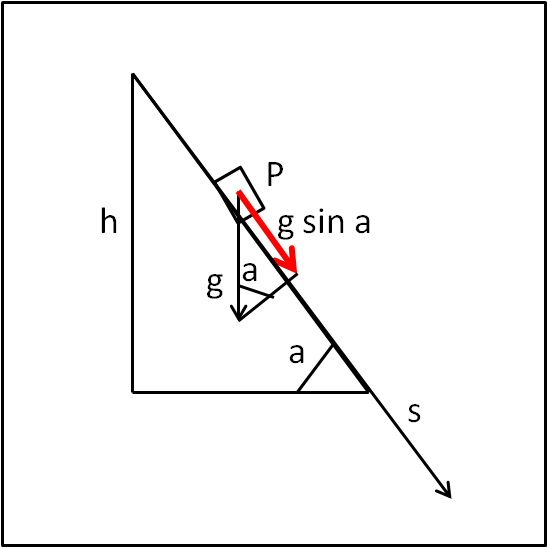
Poniamo il nostro punto P (o cubetto o quello che preferite) nella posizione più alta ed escludiamo qualsiasi attrito. Lasciamo andare P al suo destino. Cosa capita? beh, facile a dirsi: esso è soggetto solo all'accelerazione g diretta verso il basso. Tuttavia, il piano inclinato rappresenta un ostacolo alla sua caduta e solo parte dell'accelerazione agisce sul moto di P. Basta scomporre il vettore g nelle sue due componenti g cos a e g sin a, una diretta perpendicolarmente al piano inclinato e una diretta lungo il piano inclinato.

La prima componente non influisce sul moto (in pratica, fa solo stare P sulla superficie del piano inclinato). La seconda, invece, agisce proprio lungo la direzione di quest'ultimo e la possiamo considerare come asse s. Quasi magicamente, il nostro moto è diventato un moto rettilineo uniformemente accelerato, perfettamente descrivibile dalla cinematica che già conosciamo. Lo potremmo anche pensare come un moto in caduta libera, dove però, l'accelerazione g si è trasformata in g sin a. A questo punto sono applicabili tutte le formule che già conosciamo e che legano tra loro spazio, tempo, velocità e accelerazione.

Lo spazio percorso è dato da:

s = (g sin a) t²/2

Vale però anche la relazione

sin a = h/s

Possiamo perciò scrivere:

s = g h t²/2s

t² = 2 s² /hg

t = s √(2/(hg))

moltiplicando numeratore e denominatore dentro la radice per h, otteniamo

t = s √(2h/(h²g))

t = (s/h)√(2h/g)                  .... (1)

Se avessimo fatto cadere il punto P da un'altezza s = h (caduta libera) avremmo ottenuto

s = h = 1/2gt²

ossia

t_CL = √(2h/g)

Ciò vuol dire che il tempo t è s/h volte più lungo di quello t_CL in caduta libera, dato che s>h

Niente di inaspettato, ovviamente, dato che il piano è poco inclinato rispetto a una caduta libera (a = 90) e il tempo cresce.

Sembrerebbe poter anche dire che il punto P viaggia meno velocemente... E, invece, no!

Sia vf la velocità finale

vf = g (sin a) t = gt(h/s)

ma il tempo t finale è dato dalla (1)

t = (s/h)√(2h/g)

per cui, la velocità finale diventa:

vf = gh (s/h)√(2h/g)/s = √(2hg)

Questa formula è veramente fondamentale, dato che NON DIPENDE dalla lunghezza del piano inclinato, ma solo dall'altezza h. In altre parole è la stessa velocità finale che avrebbe un punto che cade da un altezza h, nella caduta libera. Infatti:

v_CL = gt = g√(2h/g) = √(2hg)

Appare veramente geniale l'idea di Galileo! Egli infatti poteva misurare un tempo anche molto lungo con gli orologi di quei tempi e avrebbe ottenuto la stessa velocità finale di un corpo in caduta libera, che sarebbe giunto al suolo in un tempo troppo breve per essere misurato.

Il piano inclinato e la sua semplice cinematica ha radicalmente cambiato la storia della Scienza.

Questo articolo è forse troppo semplice, ma chissà mai che non chiarisca le idee a qualche "principiante".