Categorie: Fisica classica Terra
Tags: Con la testa tra le nuvole equazione di Kelvin nucleazione eterogenea nucleazione omogenea
Scritto da: Fabrizio
Commenti:1
Con la testa tra le nuvole - parte 3
Tutti gli articoli della serie "Con la testa tra le nuvole" sono disponibili QUI
Nell’articolo precedente abbiamo esaminato l’effetto della tensione superficiale sulla crescita delle goccioline. La crescita delle goccioline è ostacolata dal lavoro necessario per estendere la superficie esterna delle goccioline. Il nostro criterio per valutare l’effetto sul processo di crescita delle goccioline è stato l’andamento dell’energia libera di Gibbs, G. Il processo di crescita della gocciolina per condensazione può procedere se G decresce con la crescita della gocciolina.
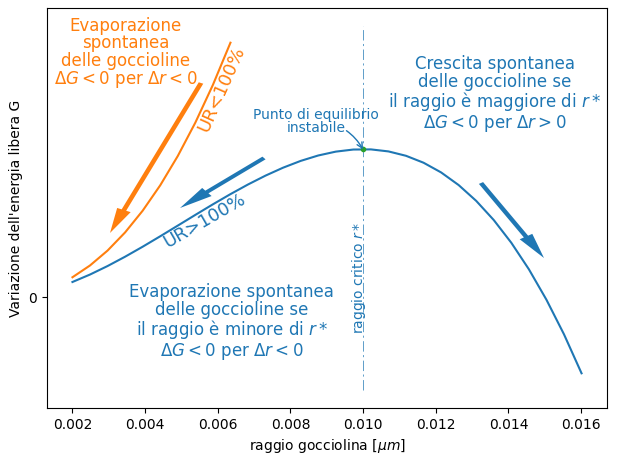
Abbiamo visto che l’andamento di G in funzione del raggio della gocciolina dipende dall’umidità relativa (UR) dell’ambiente. Per UR <100%, vapore non saturo, G decresce con la riduzione del raggio delle goccioline. Quindi le goccioline tendono ad evaporare. Per UR>100%, l’andamento di G in funzione del raggio ha un massimo. Si tratta di un punto di equilibrio instabile caratterizzato dall’umidità relativa della curva e dal raggio della gocciolina. Il raggio nel quale si trova il punto di equilibrio l’ho chiamato r* . Per raggi maggiori di r* , G decresce all’aumentare del raggio. Quindi le goccioline possono crescere spontaneamente se riescono a superare il punto di equilibrio, cioè a raggiungere un raggio maggiore di r*..
| In questo articolo esamineremo il grafico della equazione che indica i valori della umidità relativa e del raggio dei punti di equilibrio (equazione di Kelvin). Dall’esame del grafico potremo individuare dove si collocano i valori di r* per le umidità relative che si trovano usualmente nelle nuvole. Cercheremo di farci una idea della possibilità che goccioline di acqua pura possano raggiunge un raggio superiore a questi valori di r* e quindi avere la possibilità di proseguire la loro crescita. |
Nel grafico precedente si possono aggiungere altre curve per altri valori di umidità relativa, come nel grafico qui sotto. Ciascuna curva con UR>100% avrà un punto di equilibrio caratterizzato dall’umidità relativa della curva e dal raggio della gocciolina, r*, nel quale è posizionato.
La posizione dei punti di equilibrio riassume tutto il ragionamento fatto finora.
Le goccioline di raggio minore di r* tendono ad evaporare, mentre le goccioline con raggio maggiore di r* tendono a crescere per condensazione.
Il valore di r* dipende dal valore dell’umidità relativa.
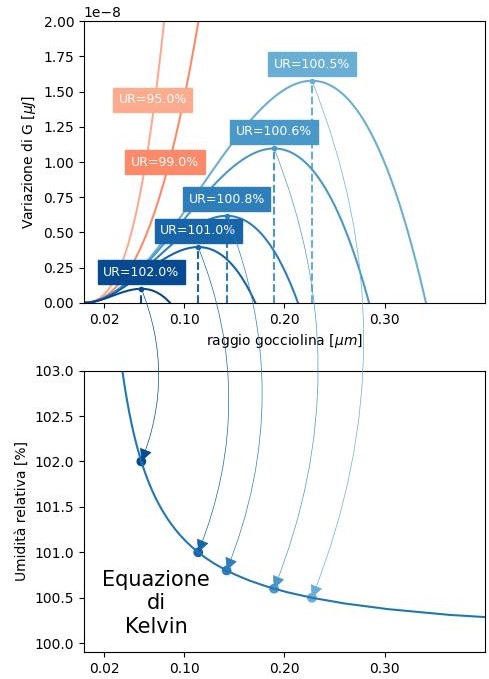
Conviene riportare in un unica curva la relazione tra valori di r* e umidità relativa dei punti di equilibrio. Si tratta della informazione più significativa ottenuta dalle curve del grafico qui affianco.
Per ciascuna curva, cioè per ciascuna umidità relativa, individuo r*. Quindi riporto i due valori in un nuovo grafico che ha nelle ascisse il raggio delle goccioline e nelle ordinate l’umidità relativa. Unendo i punti ottenuti ottengo una nuova curva che raccoglie l’informazione più significativa dell’insieme delle curve precedenti.
L’operazione illustrata graficamente sopra può essere fatta matematicamente.
Si tratta individuare i punti di massimo della funzione con la quale si ricava G noti il raggio, l’umidità relativa e la temperatura. Il massimo di questa funzione si trova dove si annullano le derivate. Poiché ci interessano i raggi critici, occorre derivare questa funzione rispetto al raggio ed uguagliare a zero il risultato.
L’equazione che si ottiene è chiamata equazione di Kelvin e corrisponde al grafico precedente. L’equazione indica quali sono i valori di r* e di umidità relativa dei punti di equilibrio ad una certa temperatura.
Nel grafico sotto riporto nuovamente l’andamento della equazione di Kelvin per fare qualche ulteriore considerazione. Ho aggiunto un secondo asse orizzontale che indica approssimativamente il numero di molecole d’acqua che contiene una gocciolina di quel raggio.
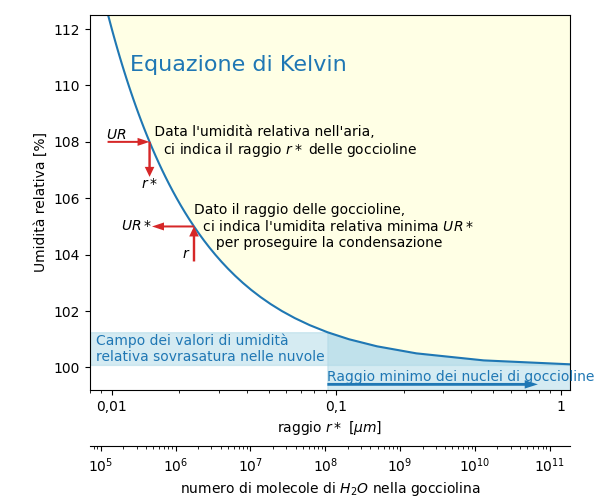
Le piccole frecce rosse indicano due possibili utilizzi della curva.
La relazione ci permette di individuare quale è l’umidità relativa minima, UR* , necessaria per far proseguire la condensazione su una gocciolina di un certo raggio, r. I punti che si trovano nell’area evidenziata in giallo rappresentano i valori di raggio della gocciolina e umidità relativa per i quali può proseguire la condensazione.
Da notare che l’interpretazione di questo grafico è diversa da quelli visti in precedenza. Si tratta di un grafico dei punti di equilibrio. Non abbiamo più l’energia libera sulle ordinate.
Possiamo anche utilizzare la relazione per individuare su quali goccioline può procedere la condensazione data una certa umidità relativa maggiore del 100%. Vale a dire quale è il valore di r* per una certa umidità relativa. Ricordiamo che r* è il raggio minimo delle goccioline sulle quali può proseguire la condensazioni per quel livello di umidità relativa.
Quest’ultima possibilità ci è utile per confrontarci con i valori di umidità relativa misurati.
Dal confronto possiamo capire se il tipo di condensazione che abbiamo esaminato può procedere spontaneamente e condurre alla formazione delle nubi.
I valori massimi di umidità relativa che si trovano nelle nuvole sono di poche unità percentuali sopra la saturazione. I valori tipici di umidità relativa sono tra 100,1% e 101%. La zona del grafico che rappresenta questi valori di umidità relativa ed i relativi valori di r* è evidenziata in azzurro.
I valori di r*, raggio che consente alle goccioline di non evaporare con questi valori di umidità relativa, sono superiori a 0,1 μm. Vale a dire che per avviare la condensazione le goccioline devono già contenere almeno centinaia di milioni di molecole d’acqua. Nuclei di così tante molecole di acqua non si creano in natura in quantità tale da permettere la formazione delle nubi.
Lo strumento teorico utilizzato dai fisici per provare questa affermazione è la teoria cinetica. La teoria cinetica permette di calcolare la frequenza con la quale si possono formare aggregati di molecole d’acqua di raggio maggiore di r* del punto di equilibrio per un dato valore di umidità relativa. L’applicazione della teoria cinetica ci dice che per i valori di umidità relativa presenti nelle nuvole, la frequenza con la quale si formano aggregati di molecole d’acqua con raggio maggior di r* è estremamente bassa, praticamente nulla.
L’acqua pura da sola non ce la fa a formare le nubi nelle condizioni presenti normalmente nell’atmosfera.
Poiché le nubi si formano, ci deve essere qualche altro meccanismo che permette di superare questo ostacolo. Vengono in aiuto all’acqua le numerose piccole particelle sospese nell’aria. In particolare quelle “amiche” dell’acqua, idrofile, ancora meglio se solubili nell’acqua. Ad esempio le particelle di cloruro di sodio, ma non sono le sole. La presenza di altre sostanze oltre all’acqua nella creazione dei nuclei per la condensazione fa denominare questo processo nucleazione eterogenea. Il processo con la sola presenza dell’acqua pura che abbiamo esaminato finora è invece chiamato nucleazione omogenea.
Nel prossimo articolo vedremo come la nucleazione eterogenea riesce a far superare l’ostacolo .






1 commento
Mi viene già da ridere al pensiero che dovrai arrivare a parlare delle scie "chimiche" che ci propinano i jet