Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Il Sole è un Super Kepler che ha una sua “rotta” prefissata, non può cambiarla, ma riesce a osservare tutti i sistemi dei suoi pianeti. Oltretutto, seguendo la famosa traiettoria circolare attorno a loro, avrà sempre due punti in cui vedrà il piano dei satelliti di taglio (i famosi nodi).

Spostiamo baracca e burattini

Quello che abbiamo imparato in giro per lo Spazio, possiamo adesso applicarlo pari pari all’interno del Sistema Solare, utilizzando il Sole come telescopio spaziale. Ci occupiamo di Giove e dei suoi quattro satelliti medicei se non altro perché sono tutti ben visibili, ma il discorso cambierebbe ben poco se andassimo su Saturno o su Urano o su Nettuno (e perché no sulla Terra e la Luna). Ciò che cambia sono le caratteristiche geometriche del sistema che vogliamo studiare. In particolare, come abbiamo visto nei due articoli precedenti, il diametro del pianeta e la distanza dei satelliti dal loro “comandante”. In altra parole, dobbiamo sostituire la stella con il pianeta scelto e i suoi pianeti con i satelliti. Tutto qua. Le operazioni da fare le sappiamo molto bene e ce le hanno spiegate le Fig. 4-8 della volta scorsa. Basta aggiornarle.

La situazione che ci troviamo di fronte è quella della Fig. 9. Al centro c’è Giove e attorno a lui rivolvono quattro satelliti a distanza crescente. In questo caso vogliamo studiare le eclissi (o transiti o occultazioni, poco importa il nome) di tutti e quattro i satelliti. Ne segue che dobbiamo ricavare quattro angoli limite, uno per ogni satellite, dato che se non cambia il raggio di Giove, cambia però la distanza tra satellite e pianeta. La formula la conosciamo bene (ed è l’unica che ho introdotto e che introdurrò). Utilizziamo, ovviamente, il sistema di riferimento che già abbiamo usato con successo, ossia quello che vede come piano “fondamentale” l’equatore di Giove che possiamo ancora una volta considerare il piano in cui rivolvono tutti e quattro i suoi satelliti. Di conseguenza avremo come coordinate le declinazioni e ascensioni rette. Possiamo chiamarle tranquillamente “giovicentriche”. In altra parole, analizziamo la faccenda da Giove, come abbiamo fatto per le stelle.

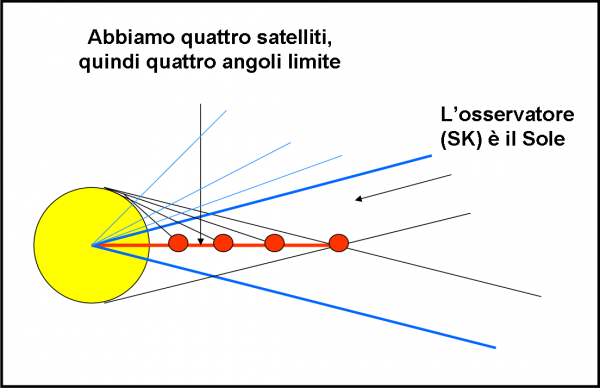
A differenza di Kepler e di Super Kepler, questa volta conosciamo tutti i parametri che possono interessarci: il raggio del pianeta e la distanza dal pianeta. Ci vuole, quindi, un attimo per calcolare la declinazione limite che permette ancora di osservare dal Sole il transito di un satellite davanti a Giove. Come già detto, ne dobbiamo calcolare quattro, dato che quattro sono i satelliti, ossia Io, Europa, Ganimede e Callisto. I risultati del banale calcolo richiesto dalla formuletta che esiste tra raggio, distanza e angolo massimo, sono riportati nella parte alta della Fig. 10.

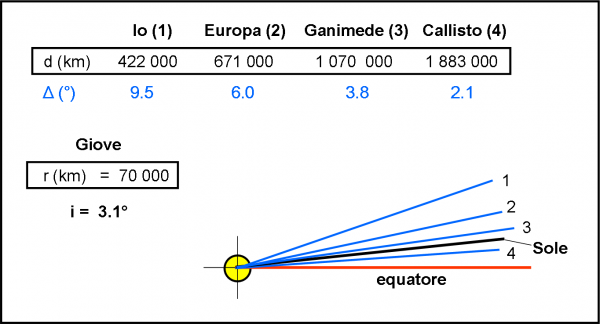
Come vedete, si hanno angoli via via più piccoli a mano a mano che il satellite si allontana. Beh… risultato più che ovvio ricordando la formula o anche solo guardando la Fig. 9.  Con questi dati in mano possiamo facilmente disegnare una figura come la Fig. 6 o 7 o 8, in cui, al centro della sfera celeste, c’è Giove con il suo piano equatoriale e in azzurro i “paralleli” che hanno come declinazione quella limite, relativa a ogni satellite.

Un momento, un momento… abbiamo tutto pronto, ma ci manca ancora l’osservatore, ossia il Super Kepler da inserire con la sua orbita nella stessa figura. No, non me ne ero dimenticato. Come già detto precedentemente la parte di Super Kepler la fa il Sole. D’altra parte è proprio perfetto per lo scopo, dato che si muove rispetto a  Giove proprio su un piano che ha una certa inclinazione i rispetto all’equatore gioviano. In realtà, avviene il contrario, ma , dato che l’orbita e circolare e avviene sempre su uno unico piano, possiamo benissimo ribaltare la situazione mettendo Giove al centro (lo facciamo sempre anche tra la Terra e il Sole…). Nella Fig. 10, non ci resta allora che inserire la linea nera che è la direzione del Sole visto da Giove al momento della sua massima declinazione (a 90° dai nodi delle due orbite), ossia quando vale proprio  i, inclinazione tra orbita del Sole (Super Kepler) e piano equatoriale di Giove.

Questo angolo vale 3.1° e, se confrontato con gli angolo limite dei quattro satelliti, ci dice già una cosa importantissima. Qualsiasi sia la posizione del Sole, esso ha una declinazione sempre inferiore alla declinazione massima dei primi tre satelliti. In altre parole siamo nelle condizioni della Fig. 7. In qualsiasi momento il Sole può vedere transitare i tre satelliti davanti a Giove. Ovviamente, li vede solo quando essi sono nella giusta posizione lungo la loro orbita (ma questo valeva anche per la stella e Super Kepler). Diversa è la situazione di Callisto. Il suo angolo limite di vista è molto piccolo, solo 2.1°, più piccolo dell’inclinazione i dell’orbita di Giove rispetto all’equatore, ossia della declinazione massima del Sole (3.1°).

Questo fatto ci dice che per Callisto vale la Fig. 8, ossia non sempre il Sole vede il transito di Callisto davanti a Giove. Accidenti, ma è così grave? Assolutamente no. La differenza tra i due angoli è  molto piccola e basta che il Sole si sposti un poco verso i nodi N e N’ e la sua declinazione diventa più piccola di quella relativa alla visibilità di Callisto. Tutte queste parole, le ho riassunte nella Fig. 11, dove vi sono i  paralleli azzurri dei quattro satelliti e il percorso nero del Sole (SK). Come si vede molto bene, basta che il Sole si trovi prima di S₁ e i transiti sono assicurati anche per  Callisto. Per gli altri tre non esistono problemi, come già detto precedentemente.

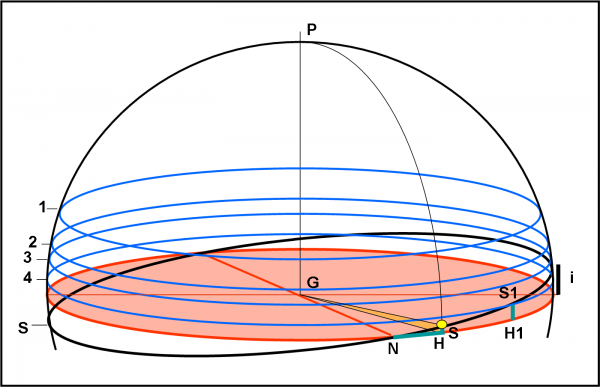
Bene, la Fig. 11 permette, se disegnata con tutta la precisione possibile, di risolvere istante per istante le condizioni di transito dei satelliti davanti a Giove. Ovviamente, tenendo  anche conto della loro rivoluzione attorno al pianeta. Fortunatamente, oggi, si conoscono perfettamente tutti i parametri in  gioco e, quindi, la previsione di questi fenomeni è un lavoro di routine che può fare benissimo il “servo” computer e i programmini che costruiscono le figure di volta in volta. L’importante, però, è che noi siamo riusciti a capire perfettamente cosa succede e perché. Non vi è dietro nessun mistero dinamico o meccanismo complicatissimo. Assolutamente no. Ci sono solo calcoli noiosi e ripetitivi che qualsiasi computer può fare. Anzi, il computer può anche tenere conto di piccole imperfezioni del nostro semplice modello.

Ad esempio, l’orbita di Giove non è perfettamente circolare così come non lo sono nemmeno quelle dei satelliti attorno a lui. Inoltre, ogni orbita ha un’inclinazione leggermente diversa e non esattamente coincidente con l’equatore del pianeta. Piccolezze che non toccano il concetto base. Leggere variazioni da inserire nelle formule da dare in pasto al calcolatore. Non vale la pena perdersi dietro a queste sciocchezze (almeno… per il nostro scopo).

Ricapitoliamo la situazione, ripetendoci ancora una volta. La situazione esistente tra satelliti, Giove e Sole, nel momento in cui quest’ultimo tocca S_1, è riportata nella Fig. 12 (parte alta). Ovviamente, per definizione, la direzione di S₁ forma proprio l’angolo limite di Callisto con il piano equatoriale (la linea azzurra di (4) coincide con la direzione del Sole). Vogliamo vedere cosa succede se ci spostassimo di 90°, ossia ci portassimo nel piano perpendicolare a quello della figura? Facilissimo: basta disegnare delle ellissi il cui semiasse maggiore è proprio il semiasse dell’orbita satellitaria, mentre il semiasse minore è dato dalla distanza dall’equatore delle intersezioni delle righe sottili (parallele alla direzione del Sole) proiettate sul piano AA’. Normalmente ciò che si vede è Giove al centro e i quattro satelliti nelle posizioni verdi (parte bassa della figura). Basta, però, aspettare e uno alla volta i satelliti transiteranno davanti a Giove, occupando le posizioni rosse. Sarebbe bello vederli tutti e quattro allineati come in figura? Sì, bello e … impossibile. Sia perché bisognerebbe avere una fortuna incredibile, che il tempo di vita del Sistema Solare non ci permetterebbe, ma -soprattutto- perché, come sappiamo bene, i primi tre satelliti di Giove sono in risonanza tra di loro (andate a rileggervi l’articolo sulle risonanze planetarie) e ripetono continuamente le stesse configurazioni, che non ammettono quella della figura…

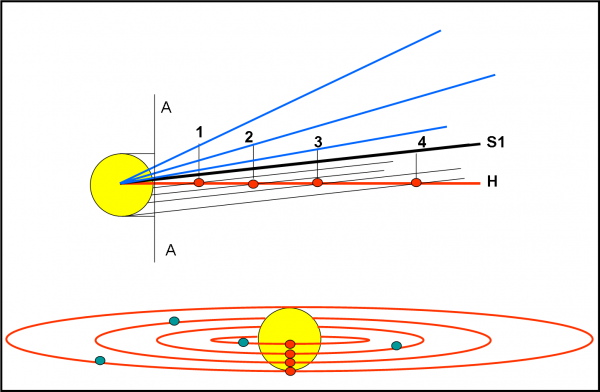
Non ho mai parlato di altre situazioni altrettanto (o quasi) interessanti. Parlo della scomparsa dei satelliti dietro a Giove. Se avete capito quanto detto finora, queste configurazioni sono estremamente banali e le lascio tranquillamente a voi…

Prima di procedere, volevo farvi notare un dato di fatto. Una figura come la parte bassa di Fig. 12 si può disegnare con foglio e matita in modo abbastanza accurato. Basta sapere la declinazione giovicentrica del Sole (ossia la declinazione eliocentrica di Giove, cambiata di segno… ridicolo!) e le dimensioni delle orbite dei satelliti. Lo schiacciamento delle ellissi la ricavate dalla parte alta, cambiando la declinazione di Giove. Veramente un gioco da ragazzi… altro che celestia o cose del genere. Potete ottenere le stesse figure da soli, con una precisione “grafica” del tutto comparabile. Quando leggete che certi programmi fanno cose mirabolanti, che sono superiori alle nostre capacità, non credeteci! Sono solo modi per mettere la polvere sotto al tappeto e non aver voglia di ragionare un poco con la propria testa…

Ben diverso è, invece, voler sapere al decimo di secondo (o anche meno) l’inizio o la fine di un transito e la perfetta geometria. In quei casi non c’è foglio e matita (ma nemmeno celestia) che tengano. Dobbiamo far lavorare il nostro schiavetto computer o andare a cercare i dati nelle tabelle già predisposte e che si trovano un po’ ovunque sul web. Se poi, volete veramente sapere cosa c’è dietro ai dati che servono al computer vi invito a dare un’occhiata QUI. Ma questo “trattato” non lo usano nemmeno celestia & co. In esso sono riportati circa 700 coefficienti correttivi che servono a definire la posizione dei quattro  satelliti rispetto ad un sistema di riferimento giovicentrico (quello che usiamo noi). Dopo la manipolazione di ben quattro matrici di rotazione, si perviene alla conoscenza delle loro posizioni viste dalla Terra e quindi al calcolo delle occultazioni/eclissi reciproche. Le posizioni sono geocentriche in quanto sono irrisori i cambiamenti temporali del fenomeno, anche per osservazioni dalla superficie terrestre, come in realtà avvengono. Gli algoritmi sono pertanto utilizzabili per qualsiasi osservatore in ogni parte del mondo. Inoltre, se si vuole andare oltre, bisogna anche tenere conto degli effetti relativistici che la massa di Giove introduce sulla luce dei satelliti che viaggia verso di noi. Meno male che ci sono gli schiavetti…

Prima di concludere questo terzo capitolo (che non è certo l’ultimo), un dovuto pensiero a Giorgia che ama molto questo tipo di articoli e si mette subito al lavoro… Se volessimo disegnare la situazione nel punto N (o N’) della traiettoria apparente del Sole, quello che vedremmo è rappresentato nella Fig. 13. Il piano equatoriale diventa una retta e i satelliti si muovono su di essa, avanti e indietro. Nasce così (teoricamente) la configurazione che ho dedicato a Giorgia (Giorgia Configuration), dato che l’aveva già preannunciata nel suo commento. Quattro per uno e uno per quattro, proprio come i moschettieri!

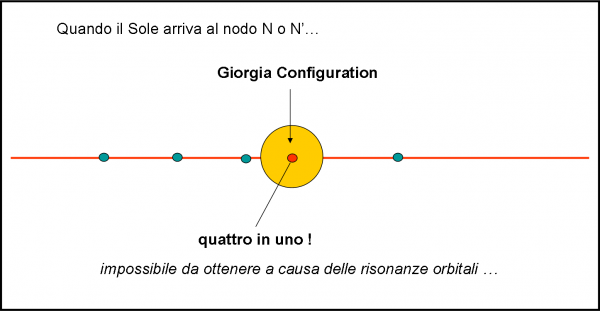
Fermiamoci qui prima di fare ancora un passetto verso il microcosmo, sostituendo Giove con i suoi satelliti, e andando a vedere cosa sono capaci di fare tra di loro. Il Super Kepler è sempre lo stesso, ossia il Sole.