Categorie: Fisica classica Relatività
Tags: primo principio della dinamica principio d'inerzia relatività galileiana sistemi inerziali
Scritto da: Vincenzo Zappalà
Commenti:3
Relatività galileiana. 2: semplifichiamo… *
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
L’esempio che ho fatto, in cui si inseriva una forza (la gravità), può avere creato un po’ di confusione. Mi permetto, allora, di semplificare ulteriormente il concetto di sistema inerziale e di primo principio della dinamica.
Il concetto importante che volevo far passare era soltanto che: “Un corpo che non subisce forze mantiene il suo stato di quiete o di moto rettilineo uniforme”. Esso è il principio d’inerzia stabilito da Galileo Galilei, che è anche chiamato primo principio della dinamica. In parole semplici, la pallina nella mano di Simplicio, che si muove di velocità vC insieme alla carrozza, anche se lasciata libera, DEVE mantenere il suo stato e quindi continuare a viaggiare alla velocità vC, ossia non muoversi rispetto a ciò che la circonda.
Ne segue che l’applicazione di una forza (gravità) non può cambiare il risultato rispetto a quello dell’esperimento eseguito a carrozza ferma. Più in generale, nessuno è in grado di giudicare se si trova in movimento a velocità costante o se è fermo, dato che nel suo sistema di riferimento nulla cambia. Ne segue che la pallina NON può cambiare percorso rispetto a Simplicio, anche se la carrozza si muove a velocità costante QUALSIASI. Ecco perché Salviati si è meravigliato. Vederla cadere ai piedi di Simplicio è assurdo.
In altre parole, sistemi di riferimento che si muovono uno rispetto all’altro con velocità costante, sono detti INERZIALI, dato che in essi vale il principio d’inerzia. Ossia, per passare da uno all’altro, devo solo cambiare la velocità, ma questo fatto non cambia le leggi fisiche.
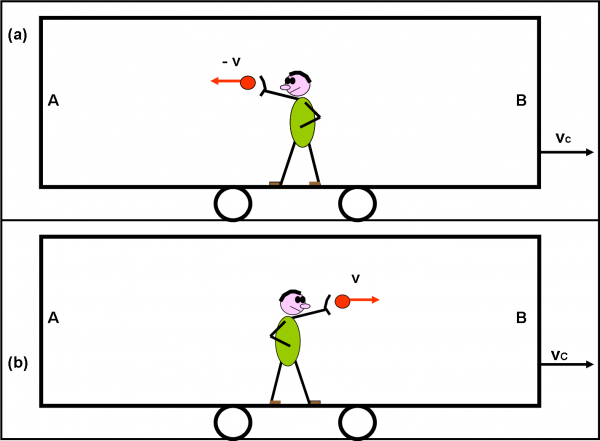
Consideriamo nuovamente la nostra carrozza, ma escludiamo del tutto la gravità. Simplicio è al centro della carrozza, equidistante dalle due pareti A e B. L’esperimento è il seguente: Simplicio lancia la pallina prima verso A e poi verso B con la stessa velocità v (imprime una forza, ma essa sparisce immediatamente quando la pallina si stacca dalla mano e si muove a velocità costante).
Divertitevi a dimostrare con qualche grafico (le formule sarebbero semplicissime, ma ci arriviamo dopo) che la pallina impiega lo stesso tempo a raggiungere la parete A e quella B, qualsiasi sia la velocità della carrozza. Il modulo della v (costante), dopo il lancio, rimane lo stesso in entrambe le direzioni, ma cambia il verso, ovviamente. E’ un giochino banale e forse inutile, ma permette di visualizzare il principio d’inerzia e l’indipendenza dell’esperimento dalla velocità della carrozza vC. Inoltre, permette già di vedere la netta differenza con quanto ci aspetterà nella relatività di Einstein. In poche parole, stiamo già parlando di relatività, ma quella galileiana, senza la quale Einstein non avrebbe potuto fare il passo in avanti.
So che sono fenomeni banali nella vita quotidiana, ma cercare di inquadrarli in un contesto rigorosamente “fisico” è essenziale per entrare col piede giusto nella relatività speciale. Fidatevi…
Ovviamente, anche Salviati, che è fuori dalla carrozza, vede accadere la stessa cosa: la pallina raggiunge le due pareti impiegando lo STESSO tempo. Potrebbe anche sembrare strano, ma invece è proprio così…
La figura mostra le due fasi dell’esperimento: in (a) la pallina è lanciata verso A con velocità v, mentre in (b) la pallina è lanciata verso B con velocità –v. Dimostrate graficamente che i tempi impiegati per raggiungere le due pareti sono identici, così come le distanze tra pallina e parete, nei due casi, istante per istante. Disegnate le vostre figure sia nel sistema di riferimento di Simplicio (immediato) che in quello di Salviati (un po’ più complicato). Ovviamente, nel secondo caso le pareti si muovono, come tutta la carrozza, a velocità vC e questa può essere qualsiasi (il sistema rimane inerziale). Riflettete bene sui risultati che ottenete graficamente. Un paio di giorni per rifletterci sopra e poi aggiungo le figure finali nello stesso articoletto… I più bravi mi perdonino…
QUI tutti gli articoli sulla Relatività Galileiana






3 commenti
Provo a cimentarmi nell'impresa, sperando di non dire troppe sciocchezze.
Ho costruito delle gif animate, per mostrare cosa vede Simplicio e cosa vede Salviati, usando una sequenza di immagini, ognuna delle quali realizzata per rappresentare la posizione dei vari oggetti nel vagone, in istanti di tempo successivi, poiché a mio avviso tale sistema permette di rappresentare almeno due dimensioni spaziali (X ed Y) ed il tempo come sovrapposizione di istanti.
Le gif mostrano tre casi diversi, visti da Simplicio (nel vagone) e visti da Salviati (sui binari).
Nel primo caso, la pallina viene prima spinta verso la direzione di moto, con una velocità identica a quella del treno, nel secondo caso viene spinta in direzione opposta con velocità uguale e contraria a quella del treno, infine la pallina viene lasciata cadere verso il pavimento.
Dato che il vagone ama il moto rettilineo uniforme, ciò che accade in questa prima gif e che vede Simplicio è esattamente la stessa cosa che accadrebbe se il vagone fosse fermo.
http://www.astrobin.com/full/105411/E/
In altre parole, indipendentemente dalla velocità del treno, il movimento della pallina verso uno dei due bordi dipende solo dal moto impresso alla pallina quando viene lanciata e lo stesso vale anche per il moto dovuto alla forza di gravità.
Senza imprimere alcun moto alla pallina, questa continuerebbe a muoversi alla stessa velocità costante del vagone.
Se la pallina viene lanciata dal centro del vagone verso un bordo, piuttosto che un altro, alla stessa velocità, coprirà l'eguale distanza nel medesimo tempo.
Simplicio, dopo aver lanciato la palla nelle due direzioni, si accorge che per compiere i 10 metri che separano la posizione centrale dai bordi del vagone, ci mette un secondo.
Simplicio conclude quindi che la palla viaggia alla velocità di 10m/sec..... proprio la stessa velocità del treno.
Fin qui, però, non vi è nulla di strano, le cose cambiano, se a vedere la stessa scena è Salviati, fermo sui binari, come mostra questa gif animata:
http://www.astrobin.com/full/105411/F/
Nel primo caso, Salviati vede la pallina che si allontana da lui, ad una velocità doppia di quella del vagone e di tutto ciò che contiene (compreso Simplicio).
Per lui dunque la pallina viaggia a 20m/sec.
Nel secondo caso, quando la pallina viene tirata in direzione contraria a quella di marcia del vagone, questa sembra addirittura ferma.
In questo caso per Salviati il vagone si allontana da lui con la stessa velocità con cui la pallina si avvicina a lui, per cui la sua distanza non varia.
Ora la pallina ha velocità zero.
Come è possibile che la stessa pallina, misuri velocità diverse?
Certo che Salviati e Simplicio non riescono proprio ad andar d'accordo!
Simplicio sia nel primo che nel secondo caso, misura la velocità, come un rapporto tra la distanza tra centro e bordi del vagone ed il tempo impiegato per compiere tale tragitto.
Quando tira la pallina questa si allontana da lui, che è al centro del vagone, e impiega 1 secondo per compiere 10 metri e raggiungere il bordo.
Salviati nel primo caso vede la pallina percorrere 20m al secondo ed il vagone 10m al secondo.
La pallina dista del bordo del vagone proprio 10 metri.
Dopo 1 secondo il vagone ha percorso 10 metri e la pallina 20 metri, ma la pallina distava dal bordo proprio 10 metri, per cui in quel secondo ha raggiunto il bordo, ossia per compiere il tragitto centro bordo ha impiegato proprio 1 secondo.
Nel secondo caso, Salviati vede la pallina ferma davanti a lui, mentre il vagone e tutto il resto fuggono in avanti.
Ovviamente non vi è nulla di magico, semplicemente la velocità impressa alla pallina è la stessa del vagone, ma ha direzione contraria.
Per Salviati la pallina è ferma, è il bordo del vagone che la raggiunge fino a travolgerla.
La pallina dopo 1 secondo, non si è mossa, ma il bordo (sinistro) del vagone che viaggia a 10 m/sec ha raggiunto la posizione della pallina (distanza bordo centro = 10 metri).
Di nuovo per coprire la distanza di 10 metri, che separano il bordo dal centro, la pallina ha impiegato 1 secondo, poco importo che per Salviati è stato il bordo a raggiungere la pallina, il risultato non cambia.
Nel terzo caso, Salviati vede la pallina cadere non perpendicolarmente al pavimento, ma con una direzione obliqua. D'altronde, la gravità imprime alla pallina una direzione di moto perpendicolare rispetto alla direzione di moto del vagone.
Quanto obliqua dipende dal rapporto tra la velocità del vagone e la velocità di caduta della pallina.
Se queste sono uguali la traiettoria avrà un angolo di 45° .
Certo che Salviati e Simplicio dovranno trovare un modo per mettersi d'accordo su come misurare la velocità.
E' plausibile questa descrizione?
Paolo
Perfetto Paolo.
come vedi, la conclusione può essere una sola: le velocità si sommano e si sottraggono in modo che la legge fisica non cambi nei due sistemi di riferimento (cambia la descrizione visiva, ma non la matematica che le descrive). Galileo su questa base ha enunciato la sua relatività che è durata fino all'avvento di Einstein. E Einstein ha detto grazie al signor Lorentz che gli ha fornito le giuste trasformazioni su un piatto d'argento... Bravo, come sempre.
Un accenno alla descrizione visiva. Se sono alla stazione e vedo passare un treno in cui un uomo fa il gioco della pallina, sono talmente abituato al fenomeno che non dirò mai che la pallina sta ferma e la parete si avvicina a lei, ma penserò che è stata tirata dall'uomo... Ormai la relatività galileiana è entrata nella realtà di tutti i giorni e, inoltre, dovrei avere una linea esterna di riferimento che difficilmente è a portata di mano se mi focalizzo su una certa azione.
Va bene... direi che posso inserire la mia figura (un po' più generale della tua). Poi enunceremo la relatività galileiana e le sue trasformazioni.
Aggiungo solo una piccola informazione, per costruire la seconda gif ho usato esattamente le stesse immagini della prima gif, solo che ho traslato queste immagini sull'asse x. Ogni immagine è stata spostata in avanti di un ipotetico identico quadratino sull'asse X (spostamento dovuto all'incremento di distanza tra vagone ed osservatore fermo sui binari, man mano che scorre il tempo..... ossia la velocità del vagone rispetto all'osservatore fermo).
Paolo