Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento

Spesso le cose banali vengono trascurate. Capitano così frequentemente nella realtà di tutti i giorni che la mente non ritiene opportuno dedicarle del tempo. Questo fatto fa apparire quasi ridicola la conclusione fondamentale di Galileo Galilei riguardo all’invarianza delle leggi fisiche in sistemi inerziali, ossia in quelli che differiscono solo per la loro velocità costante.

Simplicio che lancia la pallina con la carrozza sia ferma che in movimento non può accorgersi in alcun modo (se non guardasse fuori dal finestrino e se non ci fossero scossoni) del movimento effettuato a velocità costante: l’evento si verifica esattamente nello stesso modo.

Anche Salviati, che sta sempre fermo al di fuori della carrozza, pur descrivendo in modo diverso ciò che capita all’interno, arriva allo stesso identico risultato di Simplicio. Tutto ciò può essere scritto attraverso delle semplicissime trasformazioni di coordinate che sono nientemeno che le trasformazioni di Galileo che definiscono la sua relatività. Un concetto rivoluzionario se non altro perché espresso attraverso formule matematiche ineccepibili, anche se già intuito fin dall’antichità. La conseguenza più importante porta al concetto di somma di velocità, proprio il nocciolo della relatività di Einstein. Le trasformazioni di Galileo devono essere confrontate con quelle di Lorentz. Hanno entrambe lo stesso enorme valore fisico, non dimentichiamolo mai!

Inoltre, i grafici che sto per fare e che descrivono in modo elementare ciò che succede con carrozza ferma e con carrozza in movimento, ci portano direttamente nello spazio-tempo, ambiente naturale non solo per la relatività speciale ma anche per la MQ e per la QED.

Invito anche i più preparati a non “snobbare” quanto sto per fare, dato che è l’unica chiave per aprire la porta della fisica moderna. Galileo se lo merita!

Il teatro spaziale del nostro esperimento è la Fig. 1, ossia la carrozza, che assumiamo essere lunga 24 metri. La pallina si trova esattamente al centro e, quindi, dista 12 metri da entrambe le pareti A e B.

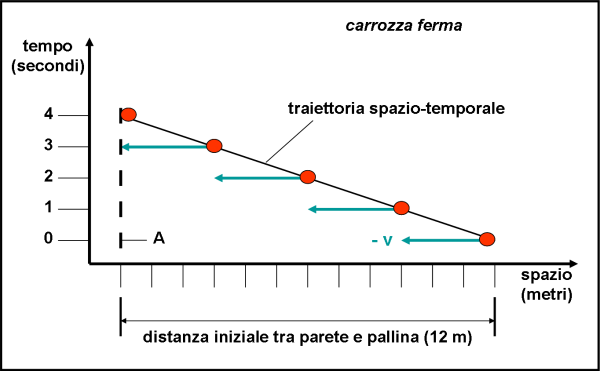
La Fig. 2 è, invece, un diagramma spazio-temporale. Esso ha in ordinata il tempo e in ascissa lo spazio. Come unità di tempo abbiamo scelto il secondo e come unità di spazio il metro. La pallina viene lanciata verso la parete A con una velocità uguale a 3 m/sec. Ciò vuol dire che ogni secondo la pallina si sposta di tre metri verso la parete A. Ho inserito il segno meno alla velocità, dato che essa va in verso opposto a quello positivo dello spazio (questa è una convenzione e niente più). Nel primo secondo la pallina si avvicina di tre metri alla parete A, nel secondo secondo di altri tre metri, nel terzo di altri tre e, infine, allo scadere del quarto, tocca la parete. Quanto tempo ha impiegato per arrivare a destinazione? Presto detto: 4 secondi. Ovviamente, lo potevamo già immaginare, dato che la distanza è di 12 metri e la pallina si muove di tre metri al secondo: 3 metri/secondo x 4 secondi = 12 metri. Vi prego… non ridete!

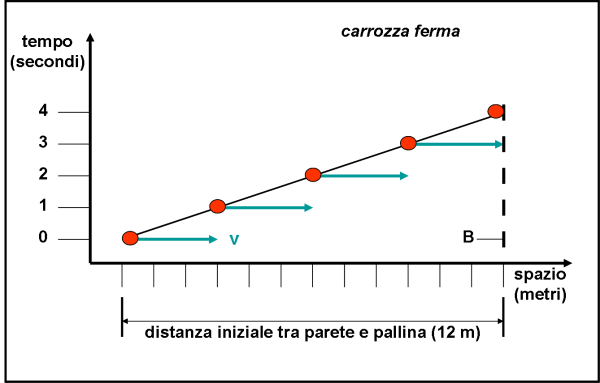
La Fig. 3 è identica alla Fig. 2, solo che questa volta Simplicio lancia la pallina dalla parte opposta, verso la parete B con una velocità uguale e contraria (lo spostamento va nel verso positivo dello spazio). Non c’è bisogno di spiegare il risultato. Come è più che ovvio la pallina toccherà B dopo 4 secondi e avrà percorso nuovamente 12 metri. D’altra parte, il modulo della velocità è costante.

Cosa vede Salviati? La stessa identica cosa di Simplicio, dato che la carrozza è ferma come è fermo lui al di fuori di essa. Non vi è nessuna velocità relativa tra di loro. Il sistema di riferimento è lo stesso per entrambi.

Mettiamo in moto la carrozza, ad esempio con una velocità (positiva) v_C di un metro al secondo. In poche parole, ogni secondo si sposta di un metro. Se guardiamo le cose dall’interno di essa, ossia attraverso gli occhi di Simplicio, non devo assolutamente fare nessuna nuova figura. Tutto ciò che è all’interno della carrozza (Simplicio, pareti e pallina nella sua mano, si muovono alla stessa velocità v_C di 1 m/sec). Simplicio non nota nessun movimento. Se non ci fosse la gravità, anche la pallina lasciata libera da Simplicio resterebbe immobile, perché anche lei deve mantenere la velocità che aveva quando era tenuta da Simplicio, proprio per il principio d’inerzia. Simplicio, perciò, non può rendersi conto del movimento che accomuna tutto ciò che sta dentro alla carrozza. Può benissimo trascurarlo e considerare ciò che capita solo rispetto al sistema di riferimento della carrozza.

Se lancia la pallina con velocità v la vede muovere verso le pareti A e B con la velocità di 3 m/sec. Per lui non è cambiato assolutamente niente. Ciò che è cambiato è solo e soltanto il sistema di riferimento utilizzato da Simplicio, ma lui non può saperlo, dato che ne fa parte. Infatti, il nuovo sistema di riferimento si muove rispetto a quello precedente di 1 m/sec, in modo costante, per cui è un sistema inerziale. Ripetiamo: non è possibile accorgersi di aver cambiato sistema inerziale, se si ci muove con lui.

Molto più interessante è ciò che vede Salviati. Lui, stando fermo nel sistema di riferimento solidale con il terreno, vede muoversi la carrozza e tutto ciò che contiene con velocità uguale a 1 m/sec. Disegniamo i diagrammi spazio-temporali osservati da Salviati. Che movimento esegue la pallina lanciata da Simplicio verso la parete A con velocità – v? (Fig. 4).

Essa è costretta a muoversi in due modi: di un metro al secondo verso destra e di tre metri al secondo verso sinistra, ossia verso la parete A. All’istante 0 la distanza tra pallina e parete A è di 12 metri. Che percorso compie nel primo secondo? Si sposta di un metro verso destra e di due verso sinistra, ossia, dato che 3 - 1 = 2, si sposta di due metri verso sinistra. Questa velocità è quella che vede Salviati ed è disegnata in rosso. Nel frattempo, però, Salviati vede anche la parete A spostarsi di un metro verso destra a causa della velocità della carrozza v_C. La distanza tra la posizione della pallina all’istante 1 e la parete A è esattamente UGUALE a quella che aveva misurato con la carrozza ferma, ossia 9 metri (12 - 2 - 1). Il procedimento non cambia all’istante 2: ai 9 metri vanno nuovamente tolti 3 metri. Dopo 4 secondi vede che la pallina tocca la parete A. In poche parole, la pallina, anche con la carrozza in movimento, ha impiegato quattro secondi per raggiungere la parete A e la distanza tra pallina e parete è diminuita costantemente di tre metri al secondo. La legge del moto è identica a quella descritta da Simplicio, che si sente fermo all’interno della carrozza, ed è identica a quella descritta con la carrozza realmente ferma.

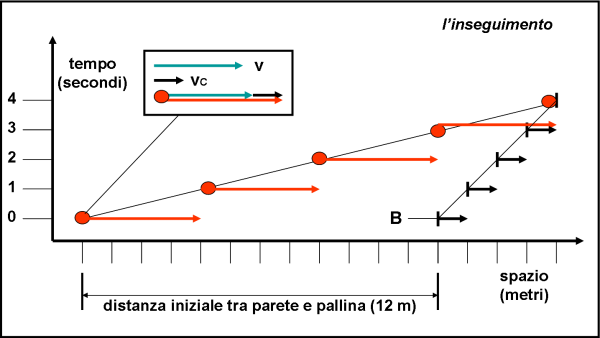
La situazione non cambia se Simplicio lancia la pallina verso la parete B, come descritto nella Fig. 5. Questa volta la velocità della pallina si somma alla velocità della carrozza. Ne risulta una velocità di 4 metri al secondo, ossia dopo un secondo la pallina si è avvicinata alla parete B di 4 metri. Tuttavia, dopo un secondo, anche la parete B si è spostata di un metro verso destra per effetto di v_C. Non ci meravigliamo di certo se all’istante 1 la distanza tra pallina e parete è nuovamente di 9 metri (12 – 4 + 1) e che dopo quattro secondi la pallina tocca la parete. Anche in questo caso il tempo impiegato è stato di 4 secondi e la distanza è diminuita di tre metri al secondo.

Che cosa abbiamo fatto per ottenere questo banale e ovvio risultato? Abbiamo solo e soltanto sommato (o sottratto) delle velocità passando da un sistema di riferimento a un altro. Nulla è cambiato nella legge del moto. Non ci resta che ottenere questo risultato molto empirico attraverso qualche semplice formuletta che descriva la trasformazione di coordinate necessaria allo scopo.

Essa è la trasformazione galileiana che è stata valida fino alle leggi di Maxwell e che ha spinto Lorentz ha introdurre una nuova trasformazione. La trasformazione di Galileo, però, rimane sempre valida se le velocità in gioco sono nettamente inferiori a quella della luce. Sono, perciò, più che sufficienti a mandare la sonda Rosetta fino alla cometa o i robottini su Marte.

Bene, abbiamo scherzato, ma dalla prossima puntata faremo sul serio…

QUI tutti gli articoli sulla Relatività Galileiana