Categorie: Fisica classica Matematica
Tags: determinanti matrici prodotto vettorile
Scritto da: Vincenzo Zappalà
Commenti:6
Momento angolare & Co. 3bis: vettori all’aMATRICIana ****
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo
Quante volte abbiamo usato delle tabelle per riassumere certi dati, mantenendo un certo ordine? La matematica non è da meno e usa una tabella particolarmente utile per una miriade di situazioni, non ultima la risoluzione di un sistema di equazioni. Noi non vogliamo entrare nei dettagli di questa enorme e importante branca della geometria analitica e dell’analisi matematica, ma la introduciamo solo per utilizzarla in alcuni casi molto particolari, come quello del calcolo delle componenti di un prodotto vettoriale.
Definiamo matrice una tabella di m ∙ n numeri (o elementi in genere) disposti su m righe e n colonne. La matrice si indica come nella parte alta di Fig. 1. Non è altro che un insieme di elementi a, b, c, … disposti per righe e colonne e delimitati da due parentesi curve. La matrice è una raccolta di dati e non un operazione in sé. Si possono, però, trasformare, moltiplicare, dividere, ecc. In particolare, si può calcolare il loro determinante, solo nel caso che la matrice sia quadrata (m = n), per ovvie ragioni matematiche come vedremo sviluppandolo.
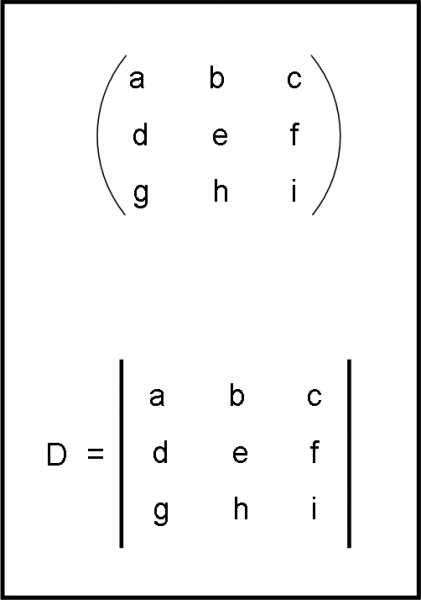
Il determinante è un certo numero o grandezza, in genere, sia scalare che vettoriale, che corrisponde a una certa matrice e che può essere calcolato seguendo certe regole. Esso si indica come la matrice, ma l’insieme degli elementi vengono delimitati da due righe verticali, come si vede nella Fig. 1, in basso. Lo possiamo chiamare Det oppure anche solo D. Riassumendo: se la matrice è una tabella, il determinante è invece una certa quantità calcolabile.
Il calcolo dei determinanti di certe matrici permette di risolvere velocemente i sistemi di m equazioni in m incognite. Noi ne usiamo uno molto particolare che ci permette di calcolare rapidissimamente il vettore prodotto vettoriale, espresso attraverso le coordinate lungo tre assi cartesiani. In particolare ne useremo uno che ha sia elementi vettoriali che numerici. Anzi… lo lascerò costruire e risolvere proprio ai più preparati di voi…
Limitiamoci ai determinanti con tre righe e tre colonne, quindi con 3 ∙3 = 9 elementi. Da loro seguono, automaticamente, quelli più semplice di 2 ∙2 = 4 elementi.
Cominciamo con quello di tre righe e tre colonne, come rappresentato in Fig. 2. Vediamo come si calcola. Consideriamo la prima riga, ossia quella formata dagli elementi a, b e c (vi dico subito che si potrebbe prendere anche un’altra riga o un’altra colonna, ma limitiamoci a questa soluzione).
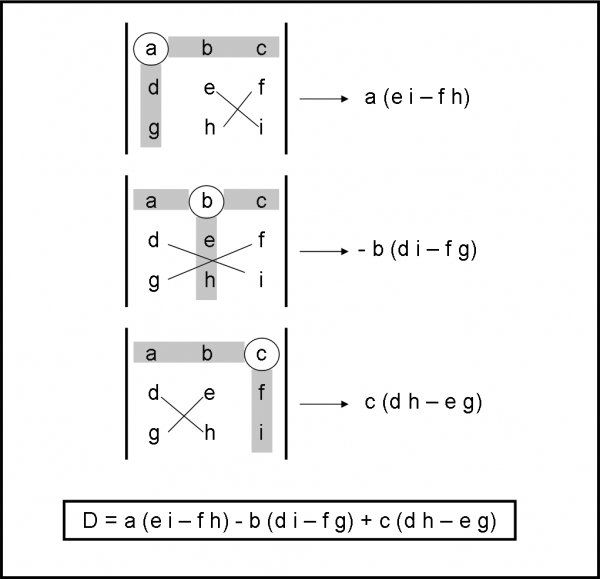
Iniziamo dal primo elemento (a). Cancelliamo, come se non ci fossero, gli elementi che stanno sulla sua riga e sulla sua colonna. Rimangono quattro elementi (e, f, h e i). Moltiplichiamoli a due a due lungo le diagonali e sottraiamo la seconda coppia dalla prima, cioè eseguiamo la seguente operazione:
e i – f h
Questa quantità la moltiplichiamo per a, ossia:
a(e i – f h)
Poi ci spostiamo sul secondo elemento (b) e eliminiamo, di nuovo, la sua colonna e la sua riga. Ci rimangono quattro elementi (d, f, g, i). Moltiplichiamoli, come prima, a due a due seguendo le diagonali e facciamo la differenza tra le due coppie, ossia:
d i – f g
Questa differenza la moltiplichiamo per b e ne cambiamo il segno, ossia:
- b(d i –f g)
Non posso spiegarvi perché dobbiamo cambiare il segno del secondo termine… ma fidatevi che deve essere fatto. Solo e soltanto al secondo termine, mi raccomando…
Passiamo al terzo e ultime elemento (c). Dopo aver cancellato la sua riga e la sua colonna, eseguiamo le solite operazioni su ciò che rimane (d, e, g, h), ottenendo:
d h – e g
e, infine, la solita moltiplicazione per c:
c(d h – e g).
Per calcolare il determinante non ci resta che sommare le tre espressioni (1), (2) e (3), così ottenute, ossia:
D = a(e i – f h) - b(d i –f g) + c(d h – e g)
Sembra una faccenda complicata, ma si impara facilmente. Ci sono molti modi per calcolare i determinanti, ma questo è quello più semplice e rapido nel caso di una matrice (sempre quadrata, ovviamente) con tre righe e tre colonne. Per matrici più grandi (non c’è limite ai termini che si possono mettere in tabella) si passa a metodi più generali e complicati. Tuttavia, alla fisica classica che lavora nello spazio a tre dimensioni, possono -normalmente- bastare tre righe e tre colonne. Lavorando nel piano basta una matrice 2 ∙2.
Applichiamo il metodo appena imparato a un determinante di una matrice di questo tipo, come mostra la Fig. 3. Le cose diventano di una semplicità disarmante…
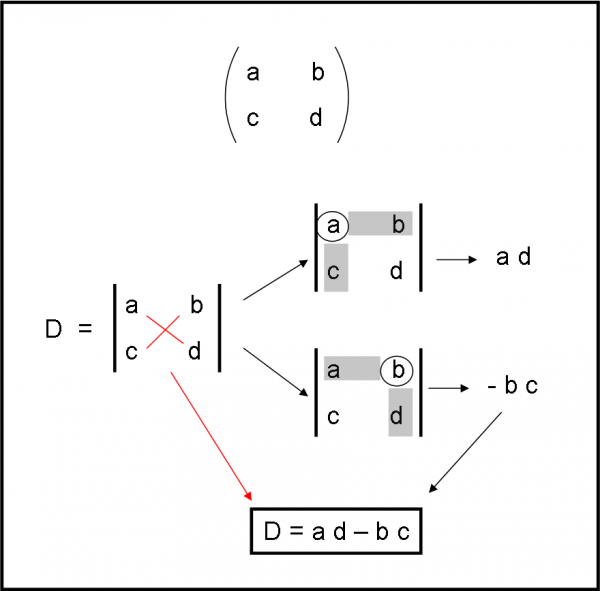
Se prendiamo il primo termine (a) e eliminiamo la sua riga e colonna non ci rimane che un unico elemento: d. Tutto ciò che si può fare e moltiplicare a per d e metterlo da parte:
a d …. (4)
Passando a b, ci rimane solo c e quindi il tutto si riduce a
- b c …. (5) ricordando di cambiare il segno di questo termine, essendo il secondo.
Il determinante sarà uguale alla somma di (4) e (5), ossia:
a d – b c.
Tanta fatica per avere ottenuto esattamente ciò che facevamo per i tre quadratini 2 ∙ 2 del determinante di tre righe e di tre colonne. Insomma, bastava moltiplicare in diagonale e fare la differenza. Beh… abbiamo imparato che il caso 2 ∙2 si risolve immediatamente moltiplicando a due a due in diagonale ed eseguendo la differenza.
Se volessimo fare i raffinati, potremmo indicare qualsiasi determinante 2 ∙ 2 come se fosse un determinante 3 ∙ 3. Basterebbe mettere qualche zero al posto giusto… ma lo vedremo presto.
In realtà, perché sto dando i… numeri in questo modo? Solo per sveltire il calcolo delle componenti del prodotto vettoriale.
In quel caso abbiamo un determinante 3 ∙ 3 molto interessante. Sulla prima riga mettiamo i tre versori i, j e k. In ogni colonna sotto di loro inseriamo le rispettive componenti dei due vettori v e u. Qualcosa come quello di Fig. 4. Sì, in questo caso è un determinante molto particolare, di tipo vettoriale e numerico, proprio come abbiamo accennato all’inizio dell’articolo.
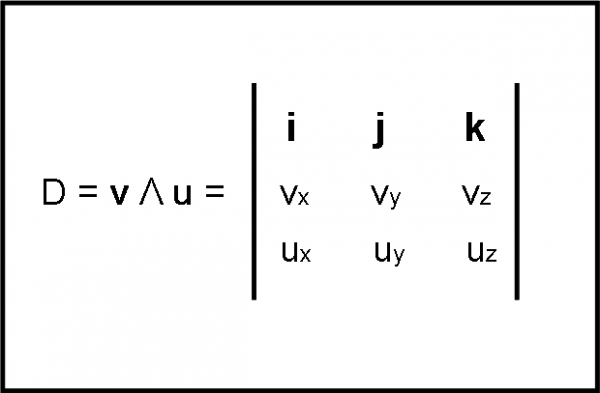
Provate a risolverlo seguendo quanto indicato precedentemente e otterrete la formula (14) del terzo articolo sul momento angolare!
Come scrivereste il determinante per ottenere la relazione più semplice (13)? Dove mettereste gli zeri? Mi raccomando… non a caso, ma secondo una logica abbastanza banale. Quali sono le loro componenti secondo il versore k (ossia l’asse z) nel caso che i due vettori siano esattamente nel piano x,y? Elementare direi…
Aggiungerò il determinante dopo avervi lasciato un po’ di tempo per provarci… Come conferma dell’esattezza del vostro tentativo avete la relazione (13).
Capito il meccanismo e presa dimestichezza, potrete calcolare tutti i prodotti vettoriali che vorrete, cambiando l’ordine dei vettori o mettendoli in direzioni particolari rispetto agli assi cartesiani o molto altro ancora…
Buon divertimento!






6 commenti
Pensavo che si parlava di spaghetti e invece vettore, momento angolare.. Arg.
e invece vettore, momento angolare.. Arg. 
Caro Enzo, ma che simpatiche che sono queste matrici, le ho appena incontrate e già mi piacciono.
Dopo lo scorso articolo mi ero chiesto cosa accomunava il risultato ottenuto per poterlo ricostruire in altro modo, ed ora eccomi accontentato!
Ho provato ad applicare il metodo che descrivi in questo splendido articolo, ottenendo i risultati della scorso articolo.
Innanzitutto ho individuato le matrici.
http://www.astrobin.com/full/105411/T/
Da quanto ricavato si ottiene che
v Λ u = i (VyUz -VzUy) -J (VxUz -VzUx) k (VxUy -VyUx)
ora:
-J (VxUz -VzUx) può essere scritta anche come:
+j (-VxUz +VzUx) ossia + j (VzUx-VxUz)
per cui si ottiene lo stesso risultato della (14)
v Λ u = i (VyUz -VzUy) + j (VzUx-VxUz) +k (VxUy -VyUx)
Le componenti (Vz e Uz) secondo il versore k (ossia l’asse z) nel caso che i due vettori siano esattamente nel piano x,y, valgono 0.
Per cui:
v Λ u = i (Vy 0 -0 Uy) + j (0 Ux- Vx 0) +k (VxUy -VyUx)
v Λ u = i (0) + j (0) +k (VxUy -VyUx)
v Λ u =k (VxUy -VyUx)
Lo stesso risultato della (13).
Paolo
caro Paolo, : un sistema ottimo per compattare un procedimento che può sembrare dispersivo. Sapessi quante cose si fanno con loro per trasformare i sistemi di riferimento, per risolvere sistemi enormi, e cento altre cose.
: un sistema ottimo per compattare un procedimento che può sembrare dispersivo. Sapessi quante cose si fanno con loro per trasformare i sistemi di riferimento, per risolvere sistemi enormi, e cento altre cose.
ero sicuro che ti sarebbero piaciute
Non diciamolo a nessuno... ma ho inserito questa appendice soprattutto per te...
Ovviamente, quello che hai descritto è giusto...
Vorrei commentare questo commento...
ci tengo in particolar modo a evidenziare i successi di Paolo non tanto per elogiarlo (ormai sa che è particolarmente bravo) quanto per l'esempio che dà riguardo all'applicazione della logica nella comprensione della matematica e quindi anche della fisica. Paolo non è uno specialista o un ricercatore. Ha sicuramente una visione logica "speciale", ma affronta tutta la matematica solo con lei, senza grosse basi alle spalle. Questo dimostra che, con un po' di applicazione e con tanto ragionamento, si ottengono risultati esaltanti e una fredda serie di formule acquista un valore quasi artistico. E' proprio giusto parlare di "estetica" della matematica... e Paolo lo dimostra dalle emozioni che prova!
Carissimi, siete proprio un gruppo di persone speciali... Vorrei fare di più, ma temo che la smania di fare troppo, comporti un decadimento delle mie umili capacità di divulgazione. Meglio poco ma bene (nei limiti della mia zucca!).
Un abbraccio a tutti (sopratutto alle ... ragazze!!!!)

ma quindi il determinante cos'e' di preciso? uno specie di risultato generato da una regola con cui si possono far interagire tra loro i valori di una matrice? un po' come il mcm e il mcd trai i numeri?
Caro Enzo, vorrei provare a fare una piccola riflessione sul metodo usato, non so se questo risponde in parte anche ad Alexander.
A mio avviso questo metodo serve per velocizzare i calcoli, nel caso in esame: il prodotto di due vettori in relazione ai versori dei tre assi cartesiani.
Guardando la tabella di figura 4 ciò che noto è che ogni colonna verticale contiene il versore e le relative componenti dei due vettori sull'asse cartesiano di riferimento.
In sintesi al versore i (asse x) corrisponde Vx e Ux, al versore J (asse y) Vy e Uy ed al versore K (asse z) Vz e Uz.
Cosa succede quando si eseguono le operazioni per determinare le matrici?
Si cancella la colonna corrispondente al versore di riferimento, in pratica se si prende in considerazione il versore i, si considerano Vx e Ux con valore zero, così è possibile semplificare l'operazione riducendo il confronto alla rappresentazione vettoriale su due assi (y e z), invece che tre (x; y e z).
Contemporaneamente è bene rammentare che il prodotto tra versori J Λ K = i e KΛ J = -i, per cui il prodotto vettoriale Vy J Λ Uz K e Vz k Λ UyJ diventa VyUz i e - VzUy i, ossia il versore risultante è i con segno positivo e con segno negativo (in base all'ordine dei vettori).
Lo stesso identico ragionamento si può fare prendendo come riferimento il versore K.
L'uso della tabella consente di sveltire tutte queste operazioni.
Ho anche cercato di capire perché è necessario cambiare di segno il secondo termine (riferimento versore J).
La risposta che mi son dato riguarda l'ordine dei versori nell'esecuzione del prodotto vettoriale (quale vettore esegue l'operazione prodotto sull'altro).
Basta vedere cosa si ottiene usando l'ordine della tabella:
Prima operazione
J Λ K = i
Seconda operazione
KΛ J = -i (segno negativo)
Prima operazione
i Λ K= -J (segno negativo)
Seconda operazione
K Λ i = J
Prima operazione
i Λ J = K
Seconda operazione
J Λ i = -K (segno negativo)
Come è facile notare il secondo termine presenta un segno negativo quando si esegue la prima operazione, al contrario degli altri due termini dove il segno negativo compare nella seconda operazione.
Cosa significa questo?
Il prodotto vettoriale diventa Vxi UzK = VxUz -J = -J VxUz e Vzi UxK = VzUx J
Per cui:
-J VxUz +VzUx J o meglio -J (VxUz -VzUx)
o, anche J (-VxUz +VzUx), J(VzUx-VxUz)
Penso che questo sia il motivo per cui il secondo termine cambia di segno... sbaglio?
Non cambiando di segno il secondo termine, si incorre nel medesimo errore grafico che avevo commesso
http://www.astrobin.com/full/78662/B/
Che peraltro produceva un errore nel calcolo del prodotto v Λ u (ho messo tra parentesi l'errore), come qui riportato:
v Λ u = vx uy K (+ vx uz J) - vy ux K + vy uz i (- vz ux J) - vz uy i
v Λ u = (vx uy - vy ux )K +( vx uz- vzux)J +( vy uz - vz uy)i calcolo errato
In realtà è stato proprio questo errore a suggerirmi perché cambiare segno al secondo termine
Paolo
cari Alex e Paolo,
dal caso particolare e un po' speciale dei versori non è facile risalire allo spirito iniziale delle matrici. D'accordo sul fatto che esse sono rappresentazioni compatte di una serie di dati. Ma, in realtà, esse riportano le informazioni che si trovano in sistemi di m equazioni in n incognite . Lo scopo principale è quello di trovare le soluzioni facendo rapporti di determinanti particolari associati alla matrice. I determinanti non sono altro che numeri associati a una certa matrice e permettono di semplificare un certo insieme di operazioni. Un altro scopo fondamentale è quello che sulle matrici si possono operare trasformazioni in modo immediato e i nuovi determinanti permettono di calcolare immediatamente le trasformazioni eseguite. Si usano tanto in geometria analitica proprio perché fanno trasferire da un sistema a un altro e via dicendo.
In realtà, nel caso dei vettori e dei versori, si sta risolvendo un sistema di tre per tre: tre vettori e tre incognite (tre perché il versore finale viene fuori da un'operazione...).
Scusate, ma a parole non è facile allargare il discorso. Non facciamo solo l'errore di partire da un caso molto particolare per cercare di comprendere il significato più generale. Sarebbe molto più giusto fare il contrario... Chissà mai che un giorno non decida di parlare di sistemi di equazioni e di risolverli con le matrici...
In ogni modo, parlando localmente la spiegazione di Paolo è ovviamente valida!