Categorie: Relatività
Tags: costanza velocità della luce De Sitter relatività speciale stelle fantasma velocità della luce
Scritto da: Vincenzo Zappalà
Commenti:7
La relatività speciale disegnata da Minkowski. 5: le stelle fantasma e la velocità della luce **
Questo articolo è stato inserito nell'approfondimento dedicato alla velocità della luce che tratta l'argomento in modo organico
La teoria della relatività formulata da Einstein estende, in qualche modo, la relatività galileiana, confermando che non solo le leggi della meccanica sono le stesse in tutti i sistemi inerziali, ma anche quelle dell’elettromagnetismo. Impone, però, un altro postulato che si riferisce alla costanza della velocità della luce.
In tal modo riesce a spiegare l’apparente incongruenza tra elettromagnetismo e fisica classica newtoniana. Sono argomenti che analizzeremo a fondo. Tuttavia, prima di iniziare nella descrizione delle ripercussioni della relatività ristretta è meglio dimostrare la costanza della velocità della luce. In altre parole, confermare che la velocità della luce non segue la relatività galileiana e rimane la stessa in tutti i sistemi inerziali.
Vi ricordate che avevamo proprio dimostrato il contrario parlando di somma delle velocità nella trasformazione galileiana, utilizzando anche alcune linee di Universo nel suo spazio-tempo. Lo spostamento, nell’unità di tempo, era relativo al sistema inerziale considerato. Se un certo corpo si muove con una certa velocità in un sistema di riferimento, anch’esso in movimento rispetto a noi, la sua velocità, misurata nel nostro sistema, è la somma di quella rispetto al sistema in movimento e di quella dello stesso sistema rispetto a noi. Insomma, la ben nota regola della somma delle velocità.
Tutto ciò potrebbe andare bene anche per Einstein, a parte il fatto che la velocità della luce non soddisfa a questa regola: essa rimane costante (nel vuoto) in tutti i sistemi di riferimento. Il che vuole anche dire che la somma della velocità della luce c e di qualsiasi altra velocità porta sempre allo stesso risultato, ossia sempre alla stessa velocità c. In altre parole, la velocità della luce non si somma ad altre velocità.
Questo postulato non distrugge la relatività galileiana, che continua a valere per velocità nettamente inferiori a quella della luce, ma, ovviamente, perde di significato per quei fenomeni, come l’elettromagnetismo, in cui “certe” particelle raggiungono velocità simili a quelle della luce.
Non esistono i fantasmi
Cerchiamo di dimostrare la costanza della velocità della luce con osservazioni astronomiche, introducendo il paradosso delle stelle fantasma di De Sitter, enunciato nel 1913, sicuramente la più geniale e semplice intuizione a riguardo. De Sitter, una grande mente raramente ricordata, si è basato su una dimostrazione per assurdo. Ossia, ha accetta la possibilità di sommare la velocità della luce ad altre velocità e ha verificato che l’ipotesi porta a un assurdo osservativo.
Senza bisogno di strane apparecchiature, né di lavorare con numeri infinitesimi, egli ha dimostrato, come ipotizzato da Einstein, che la velocità della luce non può sommarsi ad altre velocità: è quella che è, in qualsiasi sistema di riferimento ed è il valore massimo raggiungibile. Egli ha guardato direttamente all’Universo e a oggetti che si possono vedere un po’ dappertutto, a qualsiasi distanza e con caratteristiche sempre diverse. Tra tanti esempi reali, con osservazioni astronomiche “mirate”, dovevano esserci sicuramente quelli che servivano a lui.
Stiamo parlando dei sistemi binari stellari. Il “problemino” cinematico è quello illustrato nella Fig. 12.
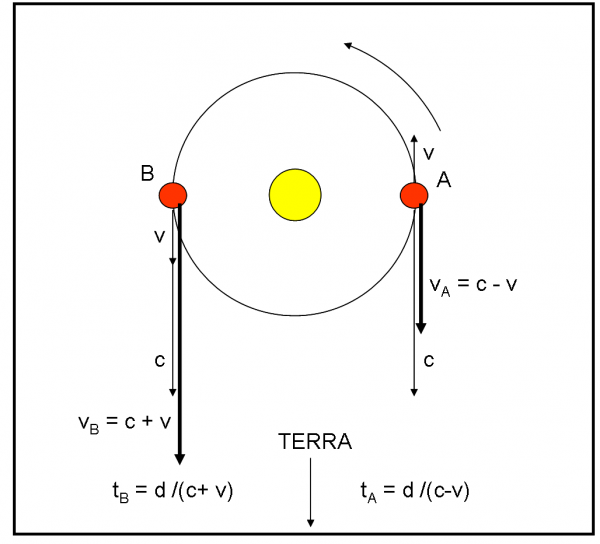
La stellina rossa rivolve attorno alla compagna gialla con un certo periodo di rivoluzione P. Consideriamo la sua posizione in A. Essa sta allontanandosi dalla Terra con velocità v. In meccanica classica, la luce che viene inviata verso di noi è determinata vettorialmente dalla velocità c della luce, a cui deve essere sottratta quella dell’astro che viaggia in senso opposto. Così, almeno, ci dice Galileo.
Quanto tempo impiega per arrivare sulla Terra la luce di A? Indichiamo con tA questo tempo e con d la distanza della stella binaria da noi. Ricordando che la velocità è uno spazio diviso per un tempo, abbiamo:
tA = d/(c – v)
Dopo mezzo periodo di rivoluzione (P/2), la stellina rossa si viene a trovare in B. In quelle condizioni, essa si muove verso di noi con velocità v. La velocità della luce e la velocità orbitale si sommano. Quanto tempo impiega ad arrivare sulla Terra la luce di B? Sia esso tB, dato da:
tB = d/(c + v)
Si vede subito che la luce partita da A viaggia più piano della luce partita da B. Ne consegue che impiega più tempo per giungere a noi (tA > tB). E’ facile calcolare la differenza tra i tempi di percorrenza della distanza d da parte della luce di A e di quella di B. Essa è data da:
tA - tB = d(1/(c - v) - 1/(c + v)) = d((c + v – c + v)/((c –v)(c + v))) = 2 d v/(c2 – v2) … (1)
Potrebbe capitare che la luce partita da A arrivi all’osservatore nello stesso istante di quella partita da B ?
Quella di A parte per prima, ma viaggia più lentamente e, quindi, potrebbe benissimo accadere. Basta che la differenza di tempo scritta in (1) sia proprio uguale alla metà del periodo di rivoluzione. Se questo fosse vero, la luce di A arriverebbe con una differenza di tempo rispetto a quella di B proprio uguale al tempo in cui la stellina rossa ha percorso metà della sua orbita. Cosa vorrebbe dire tutto ciò
Facile! L’osservatore sulla Terra dovrebbe vedere nello stesso istante la stellina sia nella posizione A che nella posizione B.
E’ una situazione impossibile da ottenere praticamente? Nemmeno per sogno. Basta che:
2 d v/(c2 – v2) = P/2.
Tra le tantissime stelle doppie osservabili ce ne sono molte che soddisfano a questa relazione. Ricordiamoci che essa dipende sia dalla velocità di rivoluzione v, sia dalla distanza d da noi, sia dal periodo P.
De Sitter ne ha identificato un certo numero, ma in nessun caso è stato possibile vedere sdoppiarsi la stellina. Essa rimane un vero “fantasma”!
L’unico modo per spiegare la mancanza degli “spettri” (quelli veri, tipo castelli inglesi…) è che:
c + v = c - v = c
Proprio come enuncia la teoria della relatività speciale.
Bello, veramente bello, e geniale!






7 commenti
Concordo con te circa la genialità di De Sitter.
dimostrazione elegante!!
Mi pare, Enzo, che sia una versione ... light dell'esperienza di Michelson e Morley (1881-1887). Loro mostrarono la necessità della contrazione spaziale per rendere il risultato dell'esperimento congruente con l'invarianza della velocità della luce.
Non mi picchiare: NON ti chiedo di spiegare quell'esperimento, cerco solo di avere un punto di contatto tra i due diversi approcci.
Più veloci della luce Enzo, chissà... i corpi materiali, ossia gli oggetti che possiedono massa, possono raggiungere al massimo la velocità della luce, e fin quì non ci piove,ma non tutte le cose possiedono massa. I fotoni, ad esempio, cioè le particelle che costituiscono la luce ma anche altre radiazioni elettromagnetiche come raggi X, raggi gamma e onde radio, non possiedono massa; quindi queste “particelle” possono viaggiare più veloci della luce? Purtroppo no; tutte le particelle che non possiedono massa o, per meglio dire, che hanno massa a riposo nulla, possono viaggiare solo ed esclusivamente alla velocità della luce(*). Quindi non più veloci di così, ma neppure meno veloci. Le particelle che non possiedono massa a volte vengono chiamate luxoni, cioè "oggetti che viaggiano alla velocità della luce”.
Questo vuol dire che non esiste proprio nulla che possa superare la velocità della luce? Forse una possibilità esiste, benché molto remota. La teoria della relatività ristretta, infatti, non esclude in modo categorico l'esistenza di particelle superluminali (cioè più veloci della luce), ma si tratta di particelle virtuali che scaturiscono dalle equazioni che descrivono la teoria, quando in esse si inseriscono i numeri immaginari. A queste particelle è stato dato il nome di tachioni che significa "oggetti che si muovono rapidamente" (dall'aggettivo greco takhýs che significa «veloce»). I tachioni dovrebbero poter viaggiare solo ed esclusivamente a velocità superiori a quelle della luce, quindi, in questo caso, mai di meno. Tutta la materia che possiede massa, come abbiamo visto, viaggia invece sempre a velocità più basse di quella della luce quindi rientra in una categoria di "corpi" che potremmo chiamare bradioni, cioè "oggetti che si muovono lentamente" (dall’aggettivo greco bradus che significa «lento»). Secondo la teoria di Einstein, pertanto, non è possibile infrangere la barriera della luce, né da una parte, né dall’altra. La velocità della luce rappresenterebbe quindi una specie di spartiacque fra i bradioni più lenti della luce e i tachioni più veloci della luce. I bradioni possono raggiungere al massimo la velocità della luce, in realtà essi possono arrivare solo a sfiorare questa velocità limite. Le equazioni di Einstein prevedono infatti che un corpo materiale aumenti la sua massa con l'aumentare della velocità fino al punto di diventare di massa infinita qualora raggiungesse la velocità della luce. Ora, poiché per spingere un corpo di massa infinita servirebbe una forza altrettanto infinita e poiché per creare una forza di intensità infinita sarebbe necessaria una quantità di energia infinita (che nell'Universo non esiste), ecco che nessun corpo materiale potrà mai raggiungere la velocità della luce. Simmetricamente i tachioni, che viaggiano in un altro "mondo", non potranno decelerare fino a raggiungere la velocità della luce perché in questo caso servirebbe una forza di intensità infinita per frenarli. Questi tachioni per il momento nessuno li ha visti e verosimilmente nessuno li vedrà mai, ma se si dovesse entrare in contatto con essi si scoprirebbe che si tratta di particelle le quali non solo non possono andare più lente della luce, ma che addirittura la loro velocità aumenta al diminuire dell'energia posseduta, al punto che se la loro energia si riducesse a zero (o quasi), la velocità diverrebbe infinita (o quasi). Essi, come detto, si ottengono quando nelle equazioni che descrivono la teoria relativistica di Einstein si inseriscono i numeri immaginari, che a loro volta sono numeri che non esistono nel campo dei numeri reali, così come non esiste la radice quadrata di un numero negativo.
La radice quadrata di un numero, come tutti sanno, fornisce un altro numero che, se elevato al quadrato, dà per risultato il numero che sta sotto radice. La radice quadrata di quattro, ad esempio, è due perché due al quadrato fa quattro. Ma, nessun numero elevato al quadrato dà come risultato un numero negativo, quindi, ad esempio, la radice quadrata di meno quattro non esiste. Tuttavia, se scomponiamo la radice quadrata di questo numero negativo in due fattori, e precisamente nella radice quadrata di meno uno e nella radice quadrata di quattro e chiamiamo la radice quadrata di meno uno «
(cioè numero immaginario), allora la radice quadrata di meno quattro darebbe per risultato 2
I tachioni sarebbero quindi oggetti di massa immaginaria e pertanto con proprietà opposte a quelli di massa ordinaria con i quali siamo abituati ad operare. Se ad esempio ad un tachione si imprime una spinta esso, invece di accelerare, rallenta. Quindi, se ad esso venisse impressa una spinta infinitamente forte, la sua velocità diminuirebbe fino a quella della luce; se invece si indebolisse il tachione sottraendogli energia esso accelererebbe fino a raggiungere velocità infinita.Abbiamo visto che i tachioni sono il risultato di un trucco matematico e pertanto probabilmente sono anch'essi un trucco, tuttavia gli scienziati li cercano ugualmente, anche se con poche speranze di trovarli. Ma ammettiamo pure che un giorno lontano si riescano ad individuare i tachioni: in che modo potremmo utilizzarli per muoverci più veloci della luce? Sicuramente non sarà possibile fermarne uno, caricarci sopra un passeggero e farlo ripartire alla volta della galassia di Andromeda. E allora?
Ebbene, esiste forse un modo per utilizzarli quali trasportatori di corpi materiali. Tutti sanno che è possibile trasformare materia in energia e viceversa, secondo una legge che scaturisce anch'essa dalla teoria della relatività. Espressa sotto forma di equazione matematica, è la seguente: E=m·c², dove E è l'energia e m la massa; c² è una costante il cui valore, elevatissimo, corrisponde al quadrato della velocità della luce. Questa legge stabilisce che ci vuole una grandissima quantità di energia per ottenere una piccolissima quantità di materia.
In effetti l'uomo è in grado, attualmente, di trasformare particelle subatomiche, come elettroni e protoni, in energia, cioè in fotoni, come pure è in grado di fare l’operazione contraria e cioè trasformare fotoni in particelle di piccola massa. Non è in grado, tuttavia, di trasformare un grosso oggetto materiale in energia, né di utilizzare enormi quantità di energia per ottenere oggetti di grosse dimensioni. Sta di fatto che coloro che lavorano più con la fantasia che con la concretezza delle cose immaginano che un giorno si potrà raggiungere questo obiettivo e, se si riuscirà a trasformare oggetti materiali in fotoni, sarà forse anche possibile trasformare oggetti materiali in tachioni.
In quest'ultimo caso il gioco sarebbe fatto. Si potrebbe allora prendere una cosa qualsiasi (anche un uomo), trasformarla in energia, cioè in luce tachionica, e spedirla a grande velocità nello spazio, per esempio con destinazione Andromeda, che verrebbe raggiunta in pochi minuti. Quindi, giunta sul luogo, la luce tachionica potrebbe a sua volta essere trasformata in materia. A parole tutto sembra semplice, ma la scienza non è fatta di sole parole. Quello che abbiamo detto, per il momento, lo si può vedere nei film di fantascienza (come già avviene) o leggere nei romanzi, ma non si può ottenere nella realtà.Da un punto di vista pratico, anche qualora i tachioni esistessero veramente, non abbiamo comunque la più pallida idea di come fare per trasformarli in materia e viceversa. E' certo invece che per essere efficace la trasformazione dovrebbe avvenire tutta contemporaneamente, cioè esattamente nello stesso istante su tutta la massa dell’oggetto da trasformare in energia pura, cosa questa non facile da realizzare. Basterebbe la differenza di qualche microsecondo per veder partire i tachioni di una parte dell'oggetto e rimanere sul posto l'altra parte con le conseguenze che si possono facilmente immaginare.Secondo gli esperti se i tachioni esistessero realmente, dovrebbe esistere anche un ambiente particolare entro il quale farli viaggiare, perché quello in cui si muovono i bradioni non sarebbe adatto. Per far volare i tachioni - dicono i fisici - sarebbe necessario uno spazio a quattro dimensioni così come, per veder volare gli aerei, è necessario uno spazio a tre dimensioni (due non bastano, mentre sono sufficienti per far viaggiare le automobili). Lo spazio a quattro dimensioni viene chiamato «iperspazio». Per capire di cosa si tratta ricorriamo ad un esempio. Immaginiamoci un veicolo (non più grande di un punto) che possa muoversi lungo un'unica linea e che non possa uscire da questa corsia obbligata. Questo veicolo sarebbe come un treno che può andare da una stazione all'altra, ma non può mai uscire dai binari (salvo incidenti). La linea viene definita uno spazio unidimensionale perché su di esso è possibile determinare la posizione di un oggetto con un solo numero. Nel caso del treno, ad esempio, basterebbe dire che si trova a 240 km dalla stazione A per conoscere esattamente la sua posizione.Immaginiamo ora che il nostro treno, per andare dalla città A alla città B debba compiere un viaggio tortuoso e che A e B siano in realtà molto vicine fra di loro tanto che se si potesse lasciare la linea ferrata, da A si raggiungerebbe B in 10 minuti. Abbandonare la linea ferrata vuol dire passare da uno spazio unidimensionale ad uno bidimensionale.
Uno spazio bidimensionale è, ad esempio, la superficie della Terra: si tratta cioè di uno spazio nel quale la posizione di un punto è determinata da due numeri. Per fissare la posizione di un punto sulla superficie terrestre servono infatti latitudine e longitudine. Su un piano si può viaggiare più liberamente e raggiungere la destinazione più velocemente di quanto non avvenga se ci si muove lungo una linea unidimensionale.Ora, se ci si sposta nell'aria, quindi attraverso uno spazio tridimensionale, si possono raggiungere velocità molto più elevate. Un aereo può viaggiare a più di 1.000 km/h e un razzo a più di 10.000 km/h. Passando quindi da un viaggio bidimensionale ad uno tridimensionale la destinazione viene raggiunta ancora più rapidamente.Forse, salendo di un altro gradino, le velocità potrebbero aumentare ulteriormente fino a diventare quasi infinite. Lo spazio a quattro dimensioni (non a tre più il tempo, come suggerisce la relatività ristretta di Einstein, ma a quattro tutte spaziali, più eventualmente quella temporale), quello che viene chiamato iperspazio, per ora esiste solo nella testa di alcune persone dotate di molta fantasia. I matematici comunque lo studiano e ne descrivono anche le proprietà geometriche, ma si tratta solo di uno studio teorico, matematico appunto.I tachioni e l'iperspazio in realtà non esistono e quindi non esiste nemmeno la possibilità di viaggiare più velocemente della luce. Accontentiamoci, per ora, di tentare di raggiungere la massima velocità possibile, cioè quella della luce, che già rappresenterebbe un bel traguardo.
Grandioso De Sitter, praticamente l'uovo di Colombo...