Categorie: Fisica classica
Tags: accelerazione gravità cinematica equazioni del moto meccanica classica moto uniformemente accelerato quiz
Scritto da: Vincenzo Zappalà
Commenti:3
SOLUZIONE dell’incontro in aria e qualche spiegazione cinematica elementare **
Per facilitare coloro che desiderano avere la soluzione del quiz, senza viaggiare su e giù tra i commenti (dove vi sono molte soluzioni esatte), la riporto passo dopo passo. Dato che Giorgia merita questo e altro per lo splendido lavoro che fa per il nostro blog, inserisco anche i passaggi fondamentali per ricavare le equazioni del moto.
Iniziamo con qualche richiamo sulle equazioni del moto e su come possono essere ricavate in modo geometrico. Per chi ha il libro sulla “Fisica addormentata nel bosco” è una ripetizione, per gli altri uno stimolo in più per acquistarlo… Può essere molto utile per una visione generale e semplificata della meccanica classica (e poi mi faccio un po’ di pubblicità…).
Ricaviamo le equazioni del moto rettilineo.
Innanzitutto, quello più semplice, ossia il moto rettilineo uniforme, ossia quello a velocità costante.
Esso nasce direttamente dalla definizione di velocità, che non è altro che lo spazio percorso nell’unità di tempo. Dato che essa è una costante, rappresenta, come ben sappiamo, il coefficiente angolare di della retta s = vt. Questa è anche l’equazione del moto, che diventa s = s0 + vt quando la retta non passa per l’origine. Tuttavia, è sempre possibile scegliere l’origine nel punto di partenza, per cui possiamo scrivere l’equazione nella forma più semplice.
s = vt
Adesso, usiamo un “trucchetto” geometrico che ci servirà tra poco. Consideriamo un sistema di coordinate in cui in ascissa vi è il tempo e in ordinata la velocità, che cosa otteniamo? Una retta parallela all’asse x. Dato un certo tempo t e una certa velocità (costante) v, cosa rappresenta il prodotto vt ? Solo e soltanto l’area del rettangolo grigio della Fig. 1. Possiamo, quindi, concludere che lo spazio percorso non è altro che l’area di un rettangolo che ha per base il tempo t e per altezza la velocità v.
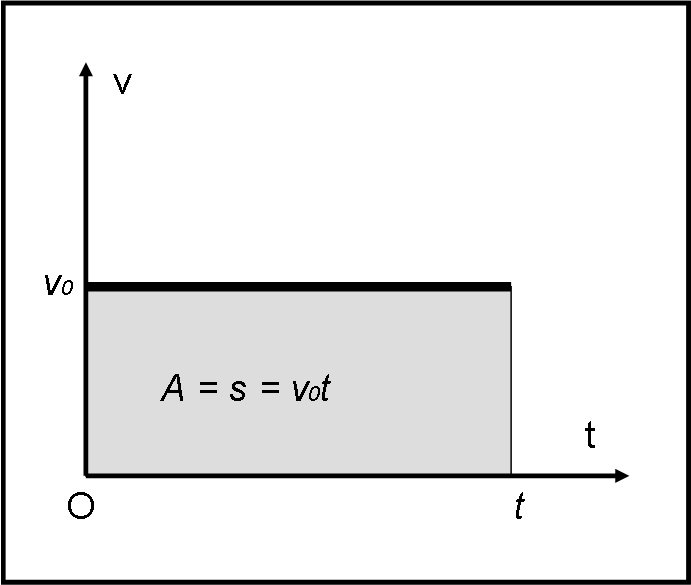
Immaginiamo, adesso, che la velocità non sia più una costante, ma vari in funzione del tempo. Tuttavia la facciamo variare in modo costante, ossia in modo che essa descriva una retta in funzione del tempo. Questa imposizione vuole dire che l’accelerazione è costante, ossia che
v = v0 + at …. (1)
La stessa cosa che avevamo usato prima per il moto uniforme, non più applicata allo spostamento, ma alla velocità. Essa rappresenta una retta nel sistema di coordinate che ha il tempo come ascissa e la velocità come ordinata. Il coefficiente angolare (costante) è adesso l’accelerazione a. v0 è, ovviamente, la velocità iniziale.
Possiamo tranquillamente disegnare la Fig. 2. La velocità è adesso una retta inclinata.
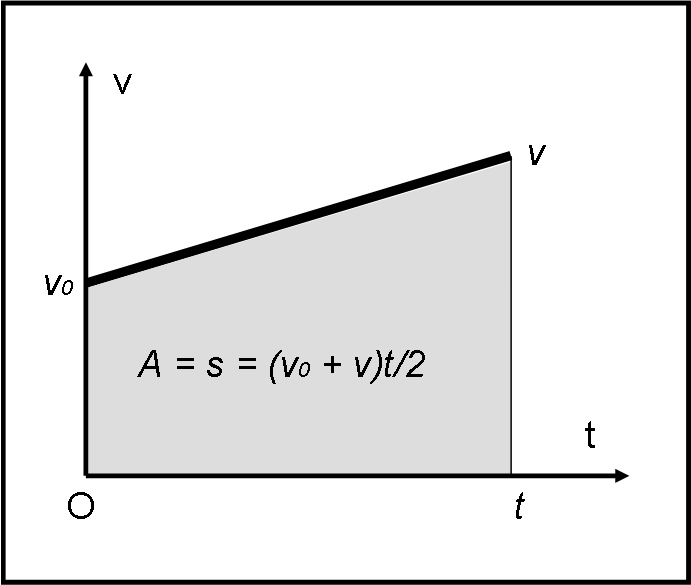
Tuttavia, anche in questo caso lo spazio percorso DEVE essere uguale all’area della figura geometrica descritta dalla velocità. Nel caso precedente era un rettangolo, dato che v era costante. Adesso è invece un trapezio rettangolo, dato che la velocità è una retta inclinata. Si ottiene, allora (area del trapezio):
s = (v0 + v)t/2 = v0t/2 + vt/2
Tuttavia, sappiamo anche da (1) che v = v0 + at e, quindi, sostituendo:
s = v0t/2 + (v0 + at)t/2 = v0t/2 + v0t/2 + at2/2
s = v0t + at2/2 …. (2)
Che è proprio l’equazione del moto uniformemente accelerato, ossia quello della caduta dei gravi.
Adesso, giochiamo un po’ con le formule (1) e (2), in modo di trasformarle in altre formule che ci possono venire utili a seconda dei dati che conosciamo e quelli che dobbiamo ricavare.
v = v0 + at …. (1)
s = v0t + at2/2 …. (2)
La prima lega tra loro velocità, tempo e accelerazione. La seconda lega spazio, accelerazione e tempo (la velocità compare solo come valore iniziale). A volte il tempo può dare fastidio e, allora, perché non cercare di eliminarlo e ricavare una formula che lega solo spazio, velocità e accelerazione? Detto e fatto.
Dalla (1) ricaviamo il tempo t, ossia:
t = (v – v0)/a
E poi lo inseriamo nella (2), ottenendo:
s = v0(v – v0)/a + a(v – v0)2/2a2 = (vv0 – v02)/a + (v2 + v02 - 2vv0)/2a
2as = 2vv0 – 2v02 + v2 + v02 - 2vv0 = v2 – v02
E, infine:
v2 = v02 + 2as ….(3)
Una relazione poco usata, ma che può venire molto utile. Abbiamo faticato un po’ a ricavarla, ma adesso possiamo usarla per qualsiasi valore di s, v0 e a.
Per finire in bellezza, ne ricaviamo anche un’altra che fa scomparire l’accelerazione nel caso del moto uniformemente accelerato. Sembra un assurdo e invece a volte può essere utile.
Partiamo nuovamente da (1) e ricaviamo at:
at = v – v0
e poi la sostituiamo nella (2):
s = v0t + (v – v0)t/2 = v0t + vt/2 – v0t/2 = v0t/2 + vt/2
s = (v0 + v)t/2 …. (4)
NOTA BENE: Trovandoci nel caso di accelerazione e/o velocità costanti siamo riusciti a scrivere le equazioni del moto attraverso semplici considerazioni geometriche (si poteva anche ragionare in puri termini di matematica elementare). In generale, però, avere l’ accelerazione e la velocità di un moto qualsiasi vuol dire avere le derivate prima e seconda dello spostamento rispetto al tempo. Per passare allo spostamento è necessario eseguire l’operazione opposta della derivata, ossia l’integrale. Questo procedimento si può usare, ovviamente, anche nel caso elementare che abbiamo trattato noi (sarebbe molto più “elegante”). In realtà, però, lo abbiamo fatto… dato che l’operazione di integrazione non è altro che una somma o -se preferite- il calcolo di un’area (la somma di tanti tratti infinitesimi porta all’area che ha per linea delimitante una curva qualsiasi). Nel caso del rettangolo e del trapezio sappiamo calcolare l’area senza problemi. Ben diversa sarebbe la situazione se la traiettoria fosse ben più complicata …
Bene, adesso possiamo risolvere il nostro problema cinematico. Riporto in Fig. 3 lo schema del problemino.
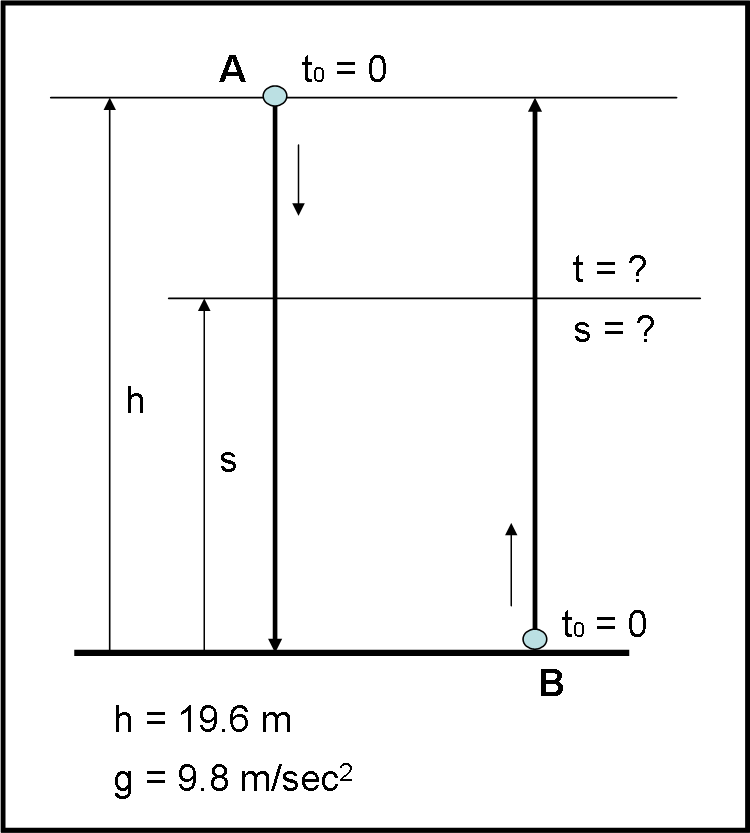
L’accelerazione che compare è quella di gravità che possiamo considerare costante, ossia a = g = 9.8 m/sec2. Scriviamo le equazioni del moto (2) per le due palline.
Quella che parte dall’alto ha v0 = 0. Essa raggiunge il punto d’incontro s dopo aver percorso il tratto h – s.
L’equazione diventa:
h – s = ½ gt2 …. (5)
Per la pallina che parte dal basso si ha:
s = v0t – ½ gt2 …. (6)
dove il segno meno è stato messo in quanto il moto si svolge in verso opposto all’accelerazione di gravità che tende a far cadere la pallina. Vi è una lotta tra la velocità che le abbiamo impartito all’inizio (v0) e il rallentamento dovuto alla gravità che tende a farla tornare indietro.
La prima cosa che vogliamo trovare è proprio la velocità iniziale che dobbiamo impartire alla pallina per farla arrivare, malgrado la gravità, fino a un’altezza h. E’ comodissimo usare la relazione (3), che non contiene il tempo…
v2 = v02 + 2as
Nel punto più alto (h), la velocità v è uguale a 0 e, quindi:
0 = v02 - 2gh
Ossia:
v0 = (2gh)1/2 = (2 x 9.8 x 19.6)1/2 = 19.6 m/sec
Sommando (5) e (6), si ha subito:
h = v0t
da cui:
t = h/v0 = 19.6/19.6 = 1 sec (tempo d’incontro delle due palline)
Dalla (5) si ottiene, immediatamente, l’altezza s:
s = v0t – ½ gt2 = 19.6 x 1 – 9.8 x 12 x 1/2 = 14.7 m
Ovviamente, si possono eseguire molte varianti, ma il risultato si ottiene sempre con relativa felicità.
Penso di continuare con questi quiz di meccanica classica, sia perché mi permettono di non pensare troppo e di fare abbastanza in fretta, sia perché ho notato che hanno avuto un gran successo di … pubblico (anche se soprattutto “passivo”).






3 commenti
Vorrei tanto essere più "attiva", prof., ma mi manca proprio il tempo di applicarmi.
Però ti assicuro che leggo i quiz, cerco di capire i vari passaggi (giusto per tenere allenato il cervello) e, sopratutto, salvo e archivio per le future generazioni!
P.S.
Qualche giorno fa mia figlia che frequenta la seconda liceo, mi ha detto che il prof. di fisica prevede di arrivare in quinta a spiegare la MQ... "tranquilla" ho esclamato "...nessun problema!"
Figurati Daniela,
so benissimo che non si può dedicare più di tanto, ma pensiamo alle future generazioni... E' già tanto quello che riesci a fare!!!
anch'io sono un ospite passivo per il tempo ristretto dato il lavoro che svolgo...però leggo spesso i tuoi articoli enzo..
devo dirti grazie perchè sto imparando nuovamente la fisica...alle superiori me la cavavo anche se la prof non era una cima ma almeno in simpatia era eccezionale