Qualcuno penserà che determinare le coordinate T’ e x’ di un certo evento P sia un gioco veramente banale, dato che non dobbiamo fare altro che tracciare dall’evento le rette parallele all’asse x’ e all’asse T’. I punti in cui queste rette intersecano gli assi T’ e x’ sono le nuove coordinate. Sì, sì, tutto giusto… ma per misurare una coordinata bisogna conoscere l’unità di misura lungo quell’asse. E noi non la sappiamo ancora, dato che non può certo essere uguale a quella con cui si misurava l’asse T e/o l’asse x. La trasformazione di Lorentz non comprime soltanto gli assi verso la retta v = c (a 45°), ma DEVE anche cambiare l’unità di misura (le vecchie e nuove coordinate sono strettamente legate tra di loro). Abbiamo davanti due strade per arrivare a un concetto fondamentale del diagramma di Minkowski. Noi, per non farci mancare niente, le useremo tutte e due.

Stiamo molto attenti a ciò che andiamo a fare. Ogni passaggio sembra un’ovvia banalità, ma il risultato è invece del tutto inaspettato o -quantomeno- ci introduce in uno spaziotempo che non è più euclideo. Seguiamo, quindi, i passaggi senza “snobbarli” assolutamente, anche se cercheremo di essere ridondanti.

Torniamo al nostro sistema di riferimento ortogonale (x,y). In Fig. 5, prendiamo un punto P e cerchiamone le coordinate. Facilissimo. Tracciamo da P la retta parallela all’asse delle y fino a che non incontri l’asse delle x. Otteniamo un punto P_x. Utilizziamo l’unità di misura che avevamo già predisposto e confrontiamola con la distanza OP_x.

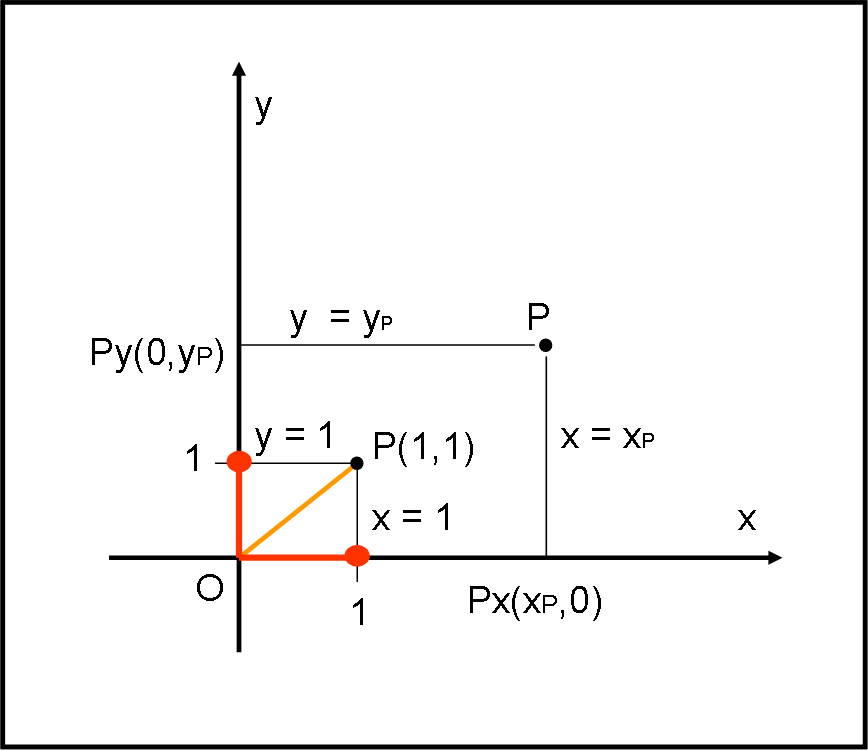
Questo procedimento ci fornisce l’ascissa  x_P del  punto P che coincide proprio con OP_x.Diciamo la stessa cosa con altre parole. Se chiamiamo x_P questa ascissa, la retta che abbiamo tracciato da P ha equazione:

x = x_P = cost

Essa descrive il luogo dei punti che hanno ascissa costante, qualsiasi sia il valore di y. L’intersezione con l’asse x è il punto P_x che ha coordinate (x_P,0). Se, il punto scelto avesse  coordinate P(1,y_P) la sua ascissa  fornirebbe l'unità di misura dell'asse x. Stesso procedimento per ricavare l’ordinata y e la sua unità di misura.

Risulta ovvio che il punto P(1,1) sta sulla retta a 45°…

No, non picchiatemi per la serie di frasi trite e ritrite che sembrano adatte per bambini delle elementari. Le ho scritte, perché, adesso, le useremo pari pari per determinare  l’unità di misura degli assi x’ e T’…

Disegniamo in Fig. 6, il nuovo sistema in movimento (x’,T’) nel piano definito da (x,T).

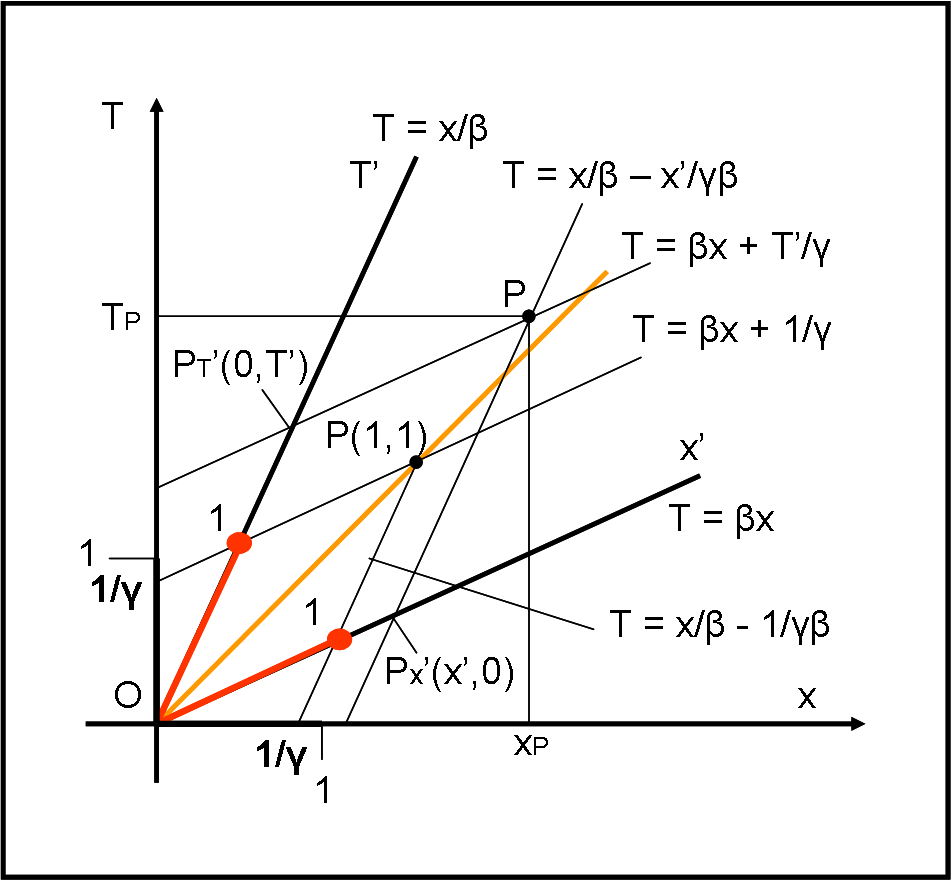
Per  averlo potuto disegnare, vuol dire che conosciamo (ossia abbiamo scelto) sia β che γ, che sono, quindi costanti per il sistema considerato. Consideriamo un evento P qualsiasi di coordinate (x,T). Cosa dobbiamo fare per trovare la coordinata T’ ? Lo sappiamo molto bene: tracciare da P la retta parallela all’asse x’ fino a che incontri l’asse T’ in P_T’. La “distanza” OP_T’ dovrebbe essere confrontata con l’unità di misura dell’asse T’, come fatto precedentemente per gli assi cartesiani x,y. Noi, però, non conosciamo l’unità di misura. Vediamo di determinarla.

Scriviamo l’equazione della retta parallela all’asse x’, passante per P. Essa si ricava dalla relazione di Lorentz:

T’ = γ(T – βx) = cost

Essa è analoga alla x = x_P = cost, scritta per il sistema (x,y), dove la costante è adesso la distanza OP_T’ .

Ricaviamo T:

T = βx + T’/γ             (con T’/γ = costante)

Questa è l’equazione di una retta passante per P descritta nel sistema di coordinate (x,y) che è quello che usiamo come riferimento. Come volevamo trovare, essa è una retta parallela all’asse x’, la cui equazione era (ricordate?):

T = βx

Per costruire l’unità di misura lungo T’ ci basta imporre che T’ = 1. L’equazione della retta diventa:

T = βx + 1/γ

A questo punto basta portare la retta fino a intersecare l’asse T, su cui abbiamo già impostato l’unità di misura. Questa retta è definita da x = 0 e quindi otteniamo:

T = 1/γ

Ma γ è una quantità nota e quindi è noto il valore di T. Questo valore è quindi misurabile facilmente sull’asse T. La strategia, allora, è molto chiara:

Dato un certo valore di γ (e quindi di v/c) è immediato segnare sull’asse T il punto che corrisponde all’unita di misura dell’asse T’. Per ottenere quest’ultimo basta tracciare dal punto (1/γ,0) la parallela all’asse x’. Dove essa incontra l’asse T’ si ha l’unità di misura dell’asse T’.

Sì, lo so, l’ho fatta lunga e potevo cavarmela con una semplice frase. Tuttavia, seguendo questo ragionamento elementare, penso che si riesca a comprendere perfettamente la deformazione dell’unità di misura.

La stessa identica cosa si può fare per determinare l’unità di misura sull’asse delle x’. Chi ha voglia, può cercare di ricavarla da solo. Di seguito, comunque, vi è la soluzione…

x’ = γ(x – βT) = cost

Ricavando nuovamente T (dobbiamo sempre scrivere una retta nel sistema T,x)

γx = γx – γβT

γβT = γx – x’

T = x/β – x’/γβ             (con x’/γβ = costante)

Questa è l’equazione di una retta passante per P descritta nel sistema di coordinate (x,T), che è quello che usiamo come riferimento. Come volevamo trovare, essa è una retta parallela all’asse T’, la cui equazione era (ricordate?):

T = x/β

Per costruire l’unità di misura lungo x’ ci basta imporre che x’ = 1. L’equazione della retta diventa:

T = x/β - 1/β γ

A questo punto basta portare la retta fino a intersecare l’asse x, su cui abbiamo già impostato l’unità di misura. Questa retta è definita da T = 0 e quindi otteniamo:

x/β - 1/β γ = 0

E ancora:

x = 1/γ

Ma γ è una quantità nota e quindi è noto il valore di x. Questo valore è quindi misurabile facilmente sull’asse x. La strategia, allora, è molto chiara:

Dato un certo valore di γ (e quindi di v/c) è immediato segnare sull’asse x il punto di ascissa 1/γ che corrisponde all’unita di misura dell’asse x’. Per ottenere quest’ultimo basta tracciare dal punto sull’asse x di ascissa 1/ γ la parallela all’asse T’. Dove essa incontra l’asse x’ si ha l’unità di misura sull’asse x’.

Come vedete si ha una deformazione uguale a quella ottenuta per l’unità di misura di T’ (ho voluto usare le stesse parole della parte precedente proprio per mostrare la similitudine).

Risulta ovvio che la retta che contiene il punto di coordinate T’ = 1 e x’ = 1 non può che essere  la retta percorsa dalla luce.

Tuttavia, vale la pena anticipare un altro concetto molto importante: lo spaziotempo che sta “sotto” la retta che indica la traiettoria della luce è uno spaziotempo molto particolare. Nessun evento che appartiene a questa parte di spaziotempo può avere una qualsiasi connessione causale con l’evento O, origine degli assi.  In poche parole, nessun evento può essere una conseguenza dell’evento O.

Non andiamo oltre, ma chi vuol pensare può già capire cosa intendo dire… lo spaziotempo di Minkowski non si limita solo a rappresentare la trasformazione di Lorentz, ma serve, soprattutto, a definire l’intero Universo relativistico (escludendo sempre l’azione della gravità). Quest’ultima frase non vi faccia pensare che sia un esercizio puramente matematico e non realistico. La relatività ristretta può essere applicata un po’ ovunque nell’Universo e viene soppiantata dalla relatività generale solo in prossimità di grandi masse.

La figura che abbiamo riportato precedentemente non si è curata di calcolare esattamente i rapporti tra l’unità nel sistema (x,T) e quella del sistema (x’,T’). Vale, però, il risultato generale che 1/γ < 1, sempre. Ma vale anche il risultato che l’unità rossa (su (x’,T’)) è più “lunga” dell’unita nera (su (x,T)), sempre. Per capire ancora meglio ciò che abbiamo ottenuto finora, la prossima volta costruiremo gli assi e le relative unità di misura per vari valori di β = v/c. Ne vedremo delle belle e lo spaziotempo apparirà -finalmente- come spazio non euclideo!