Categorie: Relatività
Tags: Minkowski relatività ristretta tempo proprio trasformazione di Lorentz unità di misura
Scritto da: Vincenzo Zappalà
Commenti:11
Il diagramma di Minkowski. 3: il cerchio si … apre **
L’esercizio da compiere è disegnare nel sistema S il sistema di coordinate S’(x’,T’) per una serie di velocità e determinare sugli assi x’ e T’ l’unità di misura corrispondente. Una pura e semplice applicazione di quanto descritto nell’articolo precedente.
Scegliamo cinque velocità v e vediamo come si opera nel diagramma di Minkowski utilizzando la trasformazione di Lorentz.
β = v/c = 0.2
S’ si sta muovendo rispetto a S con una velocità che è pari a 2/10 della velocità della luce
Disegniamo gli assi T’ e x’ attraverso gli angoli α e ϑ che gli assi formano con l’asse x.
tan α = 1/β = 5.0 à α = 79°
ϑ = 90 – α = 11°
Calcoliamo l’unità di misura su T’
γ = 1/(1 – β2)1/2 = 1.02
1/γ = 0.98
Questo valore rappresenta la T corrispondente al valore T’ = 1. In altre parole, per calcolare la “lunghezza” pari all’unità sull’asse T’ nel sistema S’, basta partire da un valore di T = 1/ γ sull’asse T e intersecare l’asse T’ con una retta parallela a x’. Il punto intersezione P’(0,1) permette di calcolare la distanza unitaria sull’asse T’, che corrisponde al segmento OP’. Distanza unitaria lungo un asse del tempo (misurata con un solo orologio) rappresenta il tempo proprio del sistema S’. Esso, infatti, indica il tempo trascorso (misurato in metri) perché l’orologio “fermo” rispetto a S’ descriva il tragitto OP’ lungo l’asse T’. In realtà, l’orologio non si muove, ma solo le sue … lancette!
Lo stesso procedimento può essere adottato per trovare l’unità di misura lungo l’asse x’. Si parte da x con il valore 1/γ e si interseca l’asse x’ con una retta parallela a T’. Il punto Q’(1,0) permette di calcolare la distanza unitaria sull’asse x’, che corrisponde al segmento OQ’.
Tracciando le rette vi accorgerete subito che è inutile rifare il calcolo per la x’. Basta, infatti prolungare la retta che passa da 1/γ e da P’ (parallela all’asse x’) fino a incontrare la retta a 45° (v = c). Da quel punto si traccia la parallela a T’ e il punto d’incontro con x’ determina il segmento OQ’ che rappresenta l’unità dell’asse x’ (distanza propria).
Quanto fatto è rappresentato nella Fig. 7
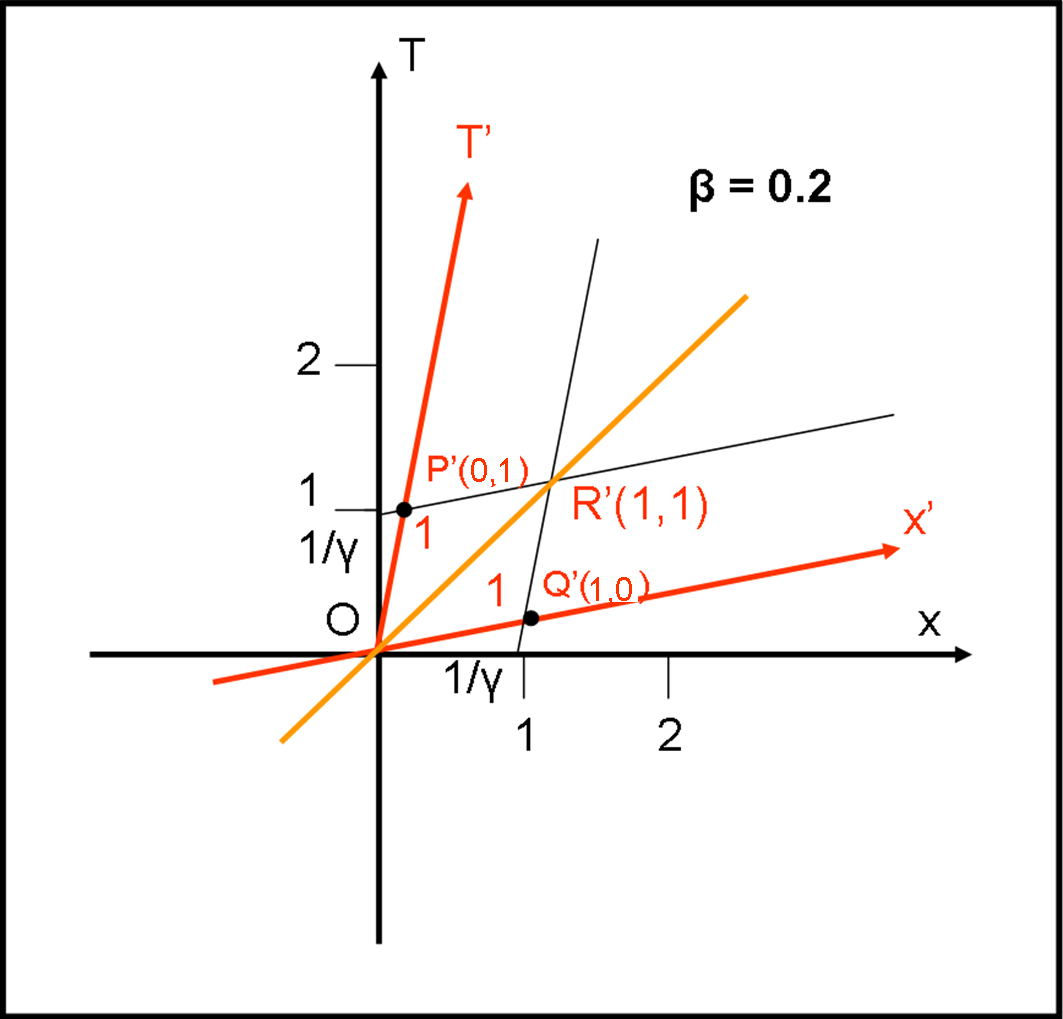
Attenzione! Non cerchiamo di confrontare le “misure” dei segmenti del piano di Minkowski come fossero segmenti euclidei. Ogni asse ha una sua unità di misura e le distanze non si conservano. Vedremo molto meglio questo concetto in seguito…
β = v/c = 0.4
tan α = 2.5
α = 68°
ϑ = 22°
1/γ = 0.92
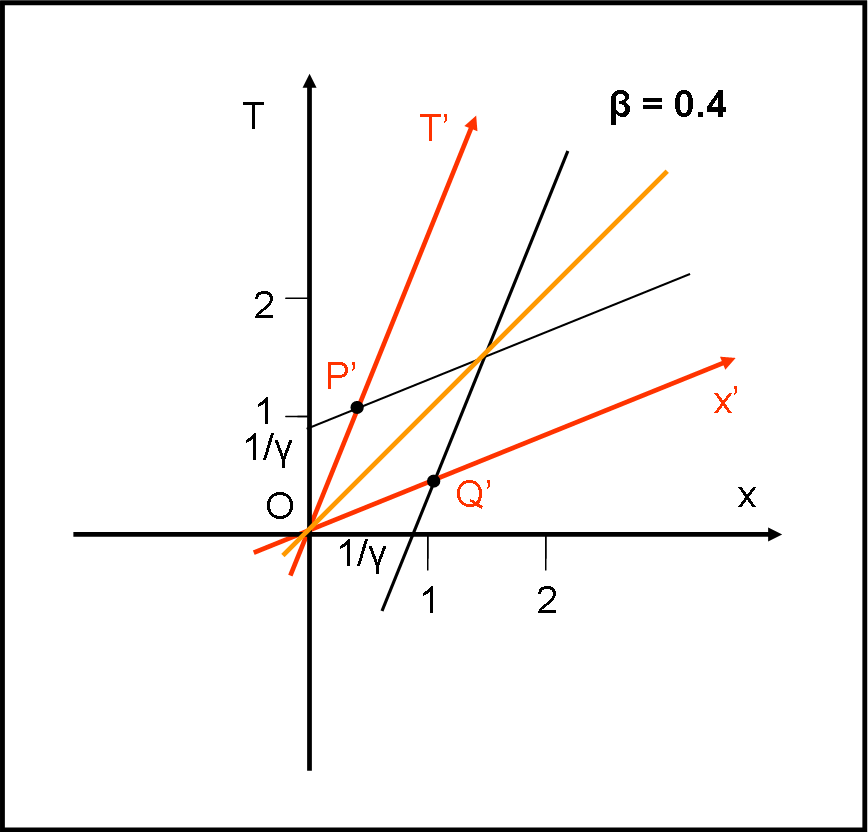
Si esegue un disegno (Fig. 
con le stesse modalità di prima e si ottengono le due nuove unità di misura che segniamo attraverso i due nuovi punti P’ e Q’. D’ora in poi non riportiamo più le figure ottenute caso e per caso, ma ci segniamo attentamente i due punti finali P’ e Q’.
β = v/c = 0.6
tan α = 1.67
α = 59°
ϑ = 31°
1/γ = 0.80
β = v/c = 0.8
tan α = 1.25
α = 51°
ϑ = 39°
1/γ = 0.60
β = v/c = 0.9
tan α = 1.11
α = 48°
ϑ = 42°
1/γ = 0.44
A questi cinque casi particolari, ne possiamo aggiungere due ancora più particolari.
β = v/c = 0.0
α = 90°
ϑ = 0°
1/γ = 1
β = v/c = 1.0
α = 45°
ϑ = 45°
1/γ = 0
Con tutte le conseguenze del caso… Per v/c = 0, le unità di misura sono proprio quelle dell’asse T e x. Per v/c = 1, gli assi T’ e x’ coincidono con la retta percorsa dalla luce e l’unità di misura diventa… infinita.
Siamo ormai vicinissimi alla conclusione di questo approccio “empirico”. Basta segnare nello spaziotempo (T,x) i vari Punti P’ e Q’ trovati, nella Fig. 9. I luoghi di questi punti (ossia quelli che descrivono le unità di misura per le varie velocità) non sono altro che due curve che hanno il vertice nei punti P’,Q’, P” e Q” (questi ultimi due ottenuti con valori negativi di T’ e x’ – notate come il “tempo” T’ sia ormai diventato una lunghezza a tutti gli effetti) e che hanno le due linee della luce come asintoti.
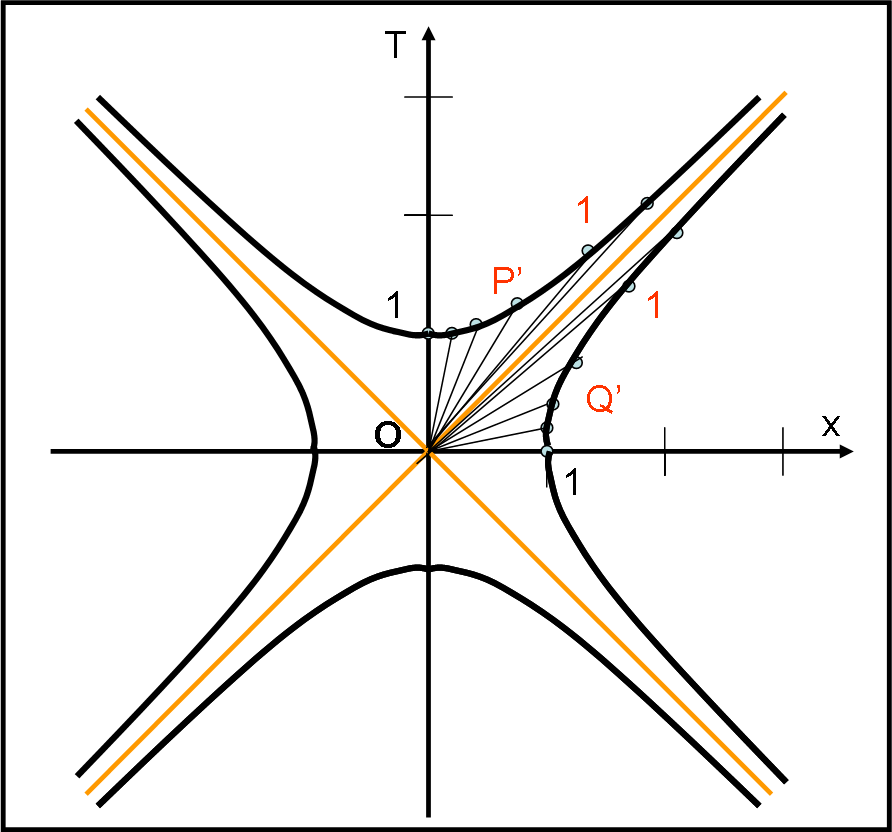
Non è difficile dimostrare che esse sono iperboli equilatere…
Ripetiamo lo strano risultato trovato: una distanza unitaria, che normalmente siamo abituati a definire come una costante, varia in funzione della velocità che si imposta e descrive una curva che è tutto meno che qualcosa che mantenga la distanza “classica”. Potrei dire, in modo un po’ misterioso, che il nostro “cerchio” si è aperto, diventando un’iperbole…
Ma questo lo vedremo più “seriamente” la prossima volta.
11 commenti
Caro Enzo, io avrei anche costruito i vari diagrammi per velocità diverse, però pensavo di aspettare a postare le figure, sperando che ciò possa servire da stimolo per altri che vogliono cimentarsi.
Non è necessario usare programmi particolari, volendo basta un foglio di carta millimetrata e/o un goniometro visto che Enzo ha indicato gli angoli per disegnare i grafici (poi con uno scanner il gioco è fatto).
Ho trovato un piccolo refuso, infatti per β = v/c = 0.8, l’angolo ϑ è di 39° e non 29° come indicato (90°-51° =39).
Inoltre nella figura 7 mi sembra che i punti P’ e Q’ riportino le coordinate invertite… provo a spiegarmi meglio: in genere nella parentesi si mette prima il valore di x e poi di y, quindi P’(1;0) io lo leggo come x’=1 e y’=0, ma a me sembra il contrario, o sbaglio?
Paolo
hai sicuramente ragione Paolo... appena posso correggo i refusi... ah la fretta!!!! Per il resto sono perfettamente d'accordo con te. Aspetta un attimo, tanto so benissimo che lo sai fare (l'avevi già spiegato la volta scorsa....)
Visto che nessuno interviene (peccato
), vi tocca accontentarvi delle figure che ho realizzato (comunque se qualcuno sta cercando di disegnarle, se posso dare un consiglio conviene leggere dopo il resto del post 
).
Ho realizzato qualche figura in più rispetto a quelle proposte negli esercizi, in pratica ho considerato valori di β da 0 ad 1, scaglionati ad intervalli di 0,1β.
Nelle figure ho riportato anche il valore degli angoli α ed θ (nel tentativo di mostrare come l'angolo tra x' ed x sia identico all'angolo tra T e T').
http://www.astrobin.com/full/34211/E/
http://www.astrobin.com/full/34211/F/
L'ultima figura mostra la posizione dei punti P'; Q' e R', in funzione dei diversi valori di β. In questa figura ho indicato anche il segmento che unisce P' all'asse T (rette parallele all'asse x') e Q' all'asse x (rette parallele all'asse T').
Una rappresentazione che ho trovato utile per sviluppare alcuni ragionamenti.
Oltre alle figure, anche per vedere meglio come il mutamento delle unità di misura in funzione di β non abbia un andamento lineare, ho realizzato due animazioni.
La prima mostra le figure di prima in sequenza.
http://www.astrobin.com/full/34211/G/
La seconda le posizioni dei punti P'; Q' e R' in sequenza:
http://www.astrobin.com/full/34211/H/
L'ultima figura mostra, nel primo grafico, come le curve tracciate prima per i punti P' e Q', se si considera anche il passato e le velocità negative, formino proprio un iperbole equilatera con le rette che rappresentano la luce come asintoti.
Nel secondo grafico (cono di luce), in cui ho indicato diverse velocità, ho cercato di dimostrare come qualunque evento si trovi nella zona tinteggiata di rosso non può in nessun modo entrare in contatto con O, poiché bisognerebbe superare la velocità della luce.
http://www.astrobin.com/full/34211/I/
Tutti questi grafici insieme ad un ragionamento sui punti di intersezione tra rette, mi hanno portato a determinare le corrispondenti coordinate x ed y (ossia nel sistema fermo) dei punti P', Q' e R'.
Riporto solo i risultati, senza descrivere il metodo che ho usato (per quello preferisco attendere i prossimi articoli di Enzo, dato che non sono certo che sia corretto e non vorrei finire solo per confondere le idee).
Coordinate dei tre punti nel sistema in movimento (x'; T'):
P' (0;1)
Q' (1;0)
R' (1;1)
Coordinate dei tre punti nel sistema fermo (x; T'):
P' (βγ; γ)
Q' (γ; βγ)
R' (1/(γ - βγ); 1/(γ – βγ) )
Ho controllato i risultati nei grafici e sembrano corrispondere.
In ultimo usando il teorema di Pitagora, penso di aver trovato anche come si determina la lunghezza dei segmenti O-P' ("distanza" misurata sull'asse T') ed O-Q' ("distanza" misurata sull'asse x').
O-P' = (βγ^2 + γ^2)^1/2
O-Q' =(γ^2 + βγ^2)^1/2
Ovviamente i due segmenti sono lunghi uguali.
In ultimo il segmento O-R' dovrebbe valere:
O-R' = (1/(γ – βγ)^2 + 1/(γ – βγ)^2)^1/2
O-R' = (2/(γ – βγ)^2)^1/2
O-R' = (2)^1/2 /(γ – βγ)
Attendo conferme su quanto penso di aver trovato.
Paolo
Gulp, come al solito troppe figure..
Paolo
Impressionante il concetto espresso con i diagrammi guardandoli mi viene in mente la curvatura dello spazio-tempo dei buchi neri solo il pensiero di addentrarmi nei segreti di questi mostri mi da i brividi.
caro Paolo,
ottima la rappresentazione... Per le conclusioni e qualche calcolo in più sulla "distanza" permettimi di andare avanti con molta calma... Preferisco non accelerare, dato che andremo a discutere sull'Universo intero... oltre che leggere direttamente dilatazione dei tempi e contrazione delle lunghezze.Puoi, comunque, già renderti conto dell'importanza unica della simultaneità: è lei che comanda in che zona di spaziotempo ci troviamo...
Ma, avanti con molta calma... Abbi pazienza e tieni il motore acceso!!!!
Caro Enzo, l’Universo rimane lì, per cui non c’è fretta.
Sai a volte mi capita (per curiosità) di provare a sviluppare alcuni ragionamenti, con la consapevolezza che questi possono contenere madornali errori, per cui ho scritto solo per me il metodo utilizzato, che mi serve per capire con i successivi articoli, dove si trovano gli errori e/o cosa funziona.
Quindi attendo volentieri i prossimi articoli.
Volevo invece chiederti, a proposito di simultaneità….
Ammettiamo che il sistema fermo (S) e quello in movimento (S’) abbiano sincronizzato ognuno i propri rispettivi orologi esclusivamente per il loro sistema di riferimento (come diceva l’alunno Einstein nel tuo articolo, almeno gli abitanti del villaggio, S fermo, qualche punto di riferimento certo lo devono pur avere), ora:
• Per il sistema “fermo” tutti gli eventi che giacciono sull’asse x al tempo T=0, sono simultanei, per cui se si fissa un tempo T qualsiasi, gli eventi simultanei giacciono sulla retta parallela all’asse x che taglia l’ordinata T al tempo fissato;
• Per il sistema in movimento tutti gli eventi che giacciono sull’asse x’ al tempo T’=0, sono simultanei, per cui se si fissa un tempo T’ qualsiasi, gli eventi simultanei giacciono sulla retta parallela all’asse x’ che taglia l’asse T’ al tempo fissato.
E’ corretta una simile “lettura” degli eventi simultanei, rispettivamente per S e per S’?
Paolo
caro Paolo,
il ragionamento è correttissimo!
Cavolo ma vi immaginate di vedere orologi che rallentano sempre e non perché hanno esaurito la carica elettrica ma perché più si avvicinano all'orizzonte degli eventi più lo spazio-tempo stesso rallenta incredibile ma così deve essere per spiegare la dilatazione spazio-temporale causata dalla forza di gravità.
Gli orologi rallentano anche senza la gravità. La gravità (relatività generale) rende il processo NON simmetrico, in quanto si deforma lo spaziotempo. Non confondiamo le due cose... Per adesso restiamo nella RR che è già abbastanza ostica...
Grazie mille Enzo
vedi io già avevo sbagliato strada menomale ci sei tu comunque molto interessanti le tue parole le terrò presente cercando di frenarmi per non svilupparmi in testa idee troppo strampalate. 