Categorie: Relatività
Tags: diagramma spazio-temporale evento lunghezza assoluta relatività galileiana relatività speciale tempo assoluto trasformazione di Galileo
Scritto da: Vincenzo Zappalà
Commenti:11
Relatività Ristretta Rivista. 2: per Galileo cambia lo spazio, ma non il tempo e le lunghezze
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
Finora abbiamo disegnato, spesso, due sistemi di riferimento in una posizione diversa, ad esempio uno sopra l’altro. Abituati come siamo alla rappresentazione secondo coordinate cartesiane, il fatto di spostarli verticalmente può creare qualche confusione, anche se “inconscia”. Ripetiamo, perciò, una banalità già detta a parole, ma non facilmente esprimibile con la grafica: lo spazio è stato ridotto a una sola linea, quella che coincide con l’asse x. Qualsiasi sistema di riferimento fa parte dello spazio e quindi qualsiasi sistema di riferimento si sovrappone a qualsiasi altro. Non è certo semplice disegnarli e confrontarli.
Stiamo, ovviamente, parlando solo di spazio, quello che abbiamo definito con tanti righelli tutti uguali, che ci permettono di misurare le distanze. Un sistema di riferimento è composto da infiniti punti e ognuno di loro può essere considerato un osservatore. Se un altro sistema si muove rispetto al primo, esistono sicuramente infiniti punti del secondo che coincidono istantaneamente con infiniti punti del primo. Proprio questa coincidenza permette agli osservatori di effettuare le misure sul secondo sistema, senza che l’informazione debba fare un percorso più o meno lungo. In altre parole, dato un punto P’ di un sistema di riferimento S’, in movimento rispetto a S, esiste sempre un punto O1 di S che coincide istantaneamente con P’. Dopo un certo periodo di tempo P’ si è spostato rispetto a S, ma vi è di nuovo un punto O2 che coincide con P’. Insomma, il punto P’ è un sorvegliato speciale e vi è sempre qualcuno che può osservarlo istante per istante.
Sto dicendo cose ovvie? Sì, lo so, ma capire esattamente il significato di osservatore può risultare importante quando si confrontano punti che si muovono a grande velocità…
Ribadiamo, perciò, che un osservatore di un sistema S non è altro che un punto qualsiasi solidale con S. La sua scelta dipende da chi e da cosa vogliamo osservare.
Tutto ciò avviene lungo la retta denominato spazio. Tuttavia, che cosa hanno di particolarmente interessante i punti P’ del sistema S’ per essere osservati? Innanzitutto, il fatto che P’ coincida con un certo osservatore O1 o O2 di S vuole dire che la posizione di P’ in un certo istante t1 o t2 è la stessa di O1 o O2, rispetto a un punto speciale O scelto come origine di S. Ricordiamo, infatti, che ogni punto di S ha una distanza da O perfettamente definita attraverso i righelli che sono stati inseriti lungo tutto il sistema. La Fig. 1 illustra la situazione.
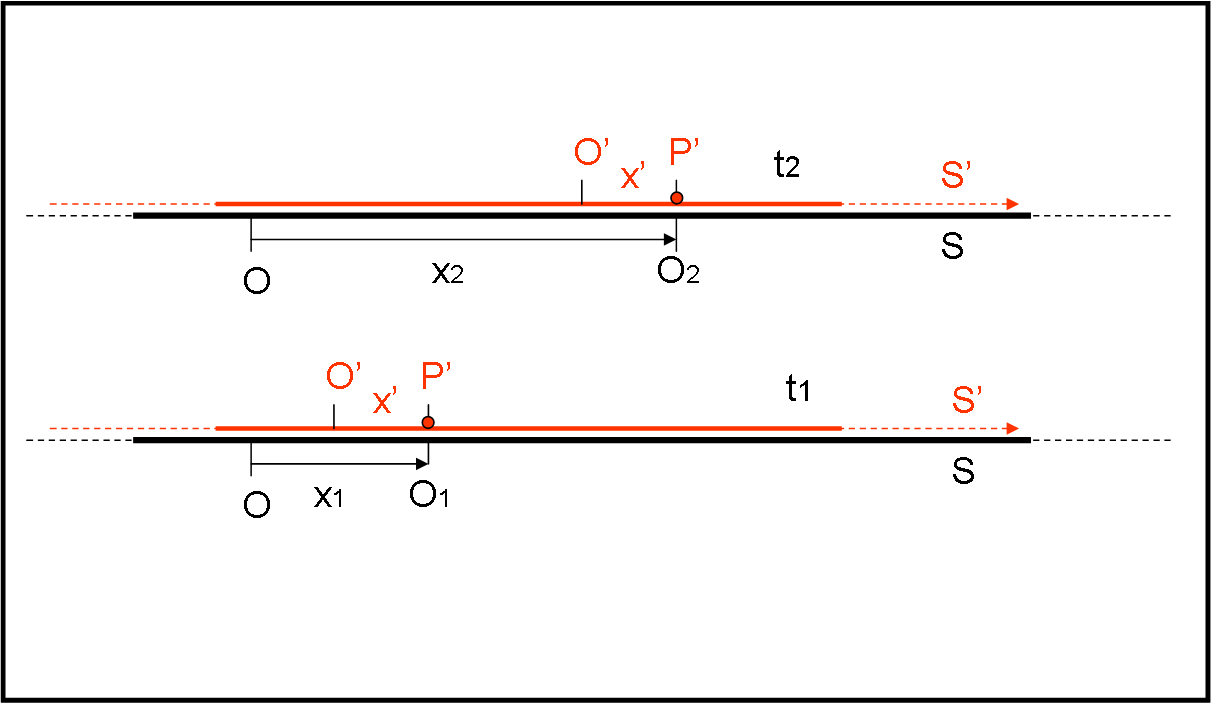
Ma anche S’ ha una sua origine O’ e i suoi bravi righelli che ne definiscono le distanze. L’osservazione di P’ permette perciò di confrontare la distanza x, rispetto a O, e quella x’ rispetto a O’.
Se poi consideriamo un'asta rigida di lunghezza L’ che si muove con S’, compresa tra P’ e Q’, il confronto con le distanze di P’ e Q’ nel sistema di S ci regala la lunghezza L dell’asta osservata (e misurata) da S. Anche questa frase sembrerebbe ovvia e banale: perché mai L’ dovrebbe essere diversa da L? L’ovvietà cade del tutto quando S’ si muove con velocità molto alta.
Ancora più importante dell’asta di S’, misurabile da S, risulta ciò di cui è dotato ogni punto di S e S’: un orologio perfetto! Anzi, è proprio l’orologio a permetterci di misurare la lunghezza L’ come viene vista da S. Gli orologi di tutti i punti di un sistema segnano sempre la stessa ora, ossia sono sincronizzati tra loro. Tuttavia, è particolarmente interessante vedere che ora segna l’orologio di P’ di S’, quando coincide con un punto O1 di S e viene osservato da quest’ultimo. Normalmente potremmo essere sicuri che segnino la stessa ora, ma , nuovamente, una velocità molto alta di S’ rispetto a S può creare grosse sorprese.
Insomma, un osservatore di S ha tante cose da osservare e da misurare, al pari di un viaggiatore di un treno, fermo alla stazione, affacciato al finestrino mentre guarda un altro treno che transita ad alta velocità sul binario adiacente.
Ovviamente, tutto quanto è stato detto, vale anche considerando S’ come fermo. Un viaggiatore del treno in corsa vede, infatti, scorrere davanti a lui tutto il treno fermo e può effettuare le stesse osservazioni e misure al pari del viaggiatore in attesa. Gli osservati diventano osservatori e viceversa!
Con l’aggiunta dell’ora segnata da un orologio, il punto di un sistema di riferimento si trasforma in evento. Esso indica non solo la sua posizione nello spazio, ma anche il momento in cui tale posizione è occupata. Uno stesso punto, benché fermo nel suo sistema spaziale, origina una serie continua di eventi, dato che cambia il tempo segnato dal suo orologio. L’introduzione del concetto di evento è di importanza fondamentale nello studio dell’Universo e della sua evoluzione.
Vediamolo sotto un altro punto di vista. Immaginiamo di essere una fata potentissima e di poter fermare l’orologio dei punti di S. Esiste ancora uno spazio ma è come se fosse congelato. Se la fata fermasse tutti gli orologi dell’Universo, tutto ciò che esiste si bloccherebbe e avremmo un intero Universo statico. Un Universo composto da punti e non da eventi. Quanto detto è di una banalità estrema, ma pensiamoci un po’ sopra e il significato diventa ben più profondo. Il tempo è una specie di motore: senza di lui niente potrebbe muoversi ed evolvere. Dato che il tempo scorre con continuità, l’Universo evolve continuamente trasformandosi in una serie infinita di eventi. Ma, per ogni istante t, potremmo dire che esiste un ben determinato Universo. Infiniti Universi separati dal minimo valore della differenza di tempo misurabile? Ve bene, va bene, torniamo a noi perché stiamo sconfinando nel mondo di Alice.
Consideriamo la Fig 2. A sinistra, in basso, abbiamo un certo sistema di riferimento il cui spazio è misurato dalle aste di lunghezza L. In tale spazio il punto P ha coordinata spaziale x0. Se il sistema è fermo (o -almeno- se si considera fermo) il punto P(x0) individua perfettamente un punto dello spazio. Tuttavia, l’orologio del punto continua girare e quindi l’evento E(x0, t) continua a mutare di “posizione” nello spazio-tempo. Non muta la coordinata spaziale, ma muta la coordinata temporale.
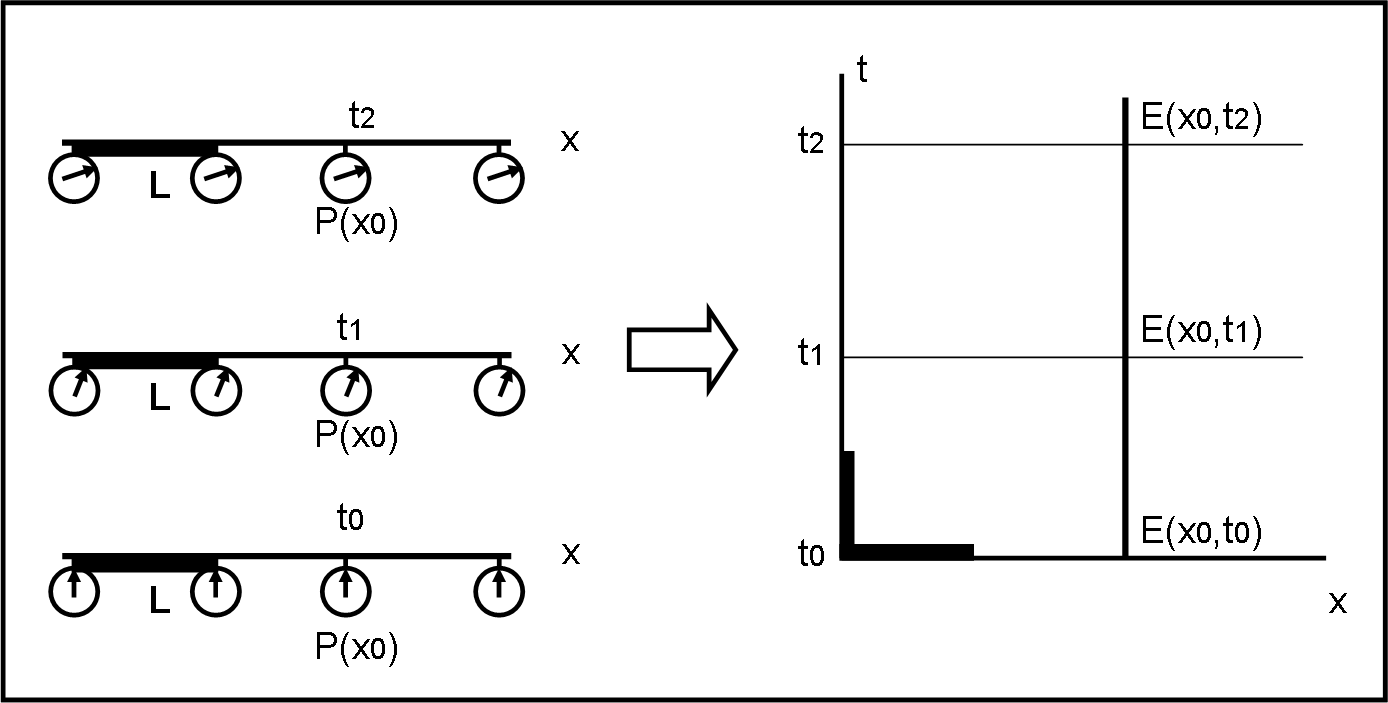
E’ venuta l’ora di semplificare la rappresentazione di sinistra ed eliminare gli orologi (almeno graficamente) e introdurre un nuovo asse che riporti più chiaramente la variazione del tempo. Ogni evento E di questo diagramma spazio-temporale è rappresentato da un punto P(x0) a cui viene associato un tempo t. Lo vediamo nella parte destra della figura. Se il punto P(x0) non si muove nello spazio, l’evento E(x0,t) si sposta lungo una retta verticale.
Dato che gli orologi di ogni punto dello spazio del sistema di riferimento segnano sempre lo stessa ora, risulta ovvio che ogni retta parallela all’asse dello spazio x indica un tempo uguale per tutti gli orologi. I due assi x e t possono perciò anche cambiare nome…
L’asse x e tutte le sue parallele rappresentano linee in cui gli orologi di un certo sistema di riferimento segnano lo stesso tempo, dato che sono stati sincronizzati perfettamente. Esse sono linee di simultaneità. Applicando questi concetti a un sistema unico la faccenda diventa oltremodo banale e perfino stupida. Ma è bene non trascurare il concetto, perché nella RR le cose non sono più così banali.
L’asse del tempo t corrisponde, invece, alla traiettoria degli eventi che non mutano la propria posizione spaziale e quindi sia lui che tutte le rette parallele possiamo anche chiamarle linee di immobilità spaziale (permettetemi questa licenza…).
Torniamo, adesso, indietro nel tempo (quello storico) e immaginiamo di accompagnare Galileo durante i suoi esperimenti. Lui si rende perfettamente conto che l’informazione luminosa non può essere istantanea, ma può permettersi di considerarla tale per almeno due motivi, uno pratico e uno concettuale. Anche se non fosse istantanea, gli strumenti a disposizione non permetterebbero di misurare la differenza tra partenza e arrivo; oltretutto, le distanze nel mondo reale sono talmente piccole che la differenza (quale che sia) può essere considerata nulla. Queste considerazioni gli permettono di enunciare qualcosa di apparentemente ovvio e banale: gli orologi di qualsiasi sistema di riferimento non solo misurano la stessa ora, ma qualsiasi orologio di qualsiasi sistema segna sempre la stessa ora anche se visto da un altro sistema di riferimento.
Questa è un’ipotesi fondamentale ed estremamente semplificativa. Tuttavia, la realtà misurabile ai tempi di Galileo sembrava essere perfettamente descrivibile attraverso questa approssimazione. Tutte queste parole si possono condensare con una uguaglianza importantissima:
t’ = t
Essa ci dice che il tempo che viene misurato in un sistema di riferimento S è assolutamente identico al tempo misurato in un altro sistema di riferimento S’, ma anche che il tempo di S’ osservato da S rimane inalterato (e viceversa). Ciò vuole anche dire che eventi che sono simultanei in un sistema di riferimento lo devono anche essere in un altro sistema di riferimento in moto inerziale rispetto al primo.
In poche parole tutti gli orologi di qualsiasi sistema di riferimento, sia fermi che in moto, segnano sempre la stessa ora, anche se visti da un altro sistema. Il tempo scorre in modo identico indipendentemente dalla velocità relativa tra i sistemi di riferimento. Ribadiamo ancora: due eventi simultanei in un sistema, lo sono anche se osservati da un altro sistema.
Questa conclusione maschera un fatto importantissimo che la RR non può accettare. Abbiamo detto che ogni punto di un sistema di riferimento ha un suo orologio che gli permette di misurare l’ora. Nello spazio-tempo di Galileo, la relazione t = t’ permette di non fare distinzione tra chi misura un certo tempo: sempre lo stesso orologio oppure orologi diversi. Nessun problema, tutti girano allo stesso identico modo.
Fatemi essere quasi ridicolo e vediamo come un sistema di riferimento fermo misura il tempo del sistema in movimento. Torniamo allo spazio, con i suoi orologi, in Fig. 3.
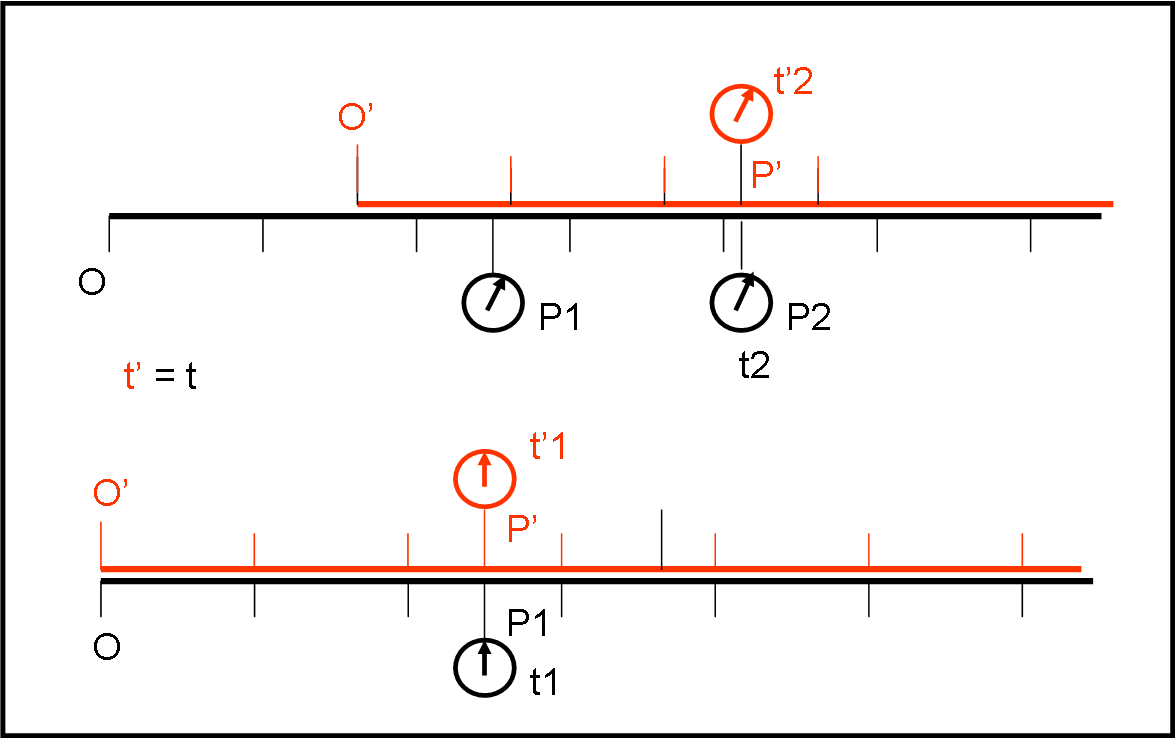
All’istante t1 (uguale a t’1 per definizione) i punti P’ e P1 coincidono spazialmente e segnano la stessa ora. Al tempo t2 > t1 vengono nuovamente confrontati gli orologi dei due sistemi di riferimento. Nel frattempo, però, il sistema S’ si è mosso spazialmente di una certa quantità. Il Punto P’, solidale con il sistema S’, si è quindi anch’esso spostato rispetto a S (considerato fermo). Il confronto tra i tempi viene eseguito tra l’orologio posto in P’ e quello di un punto P2 diverso da P1. Attenzione quindi: Nel sistema S’ la differenza di tempo viene misurata utilizzando un solo orologio, quello del punto P’, mentre nel sistema S è necessario utilizzare due orologi posti in P1 e in P2.
Per il sistema in movimento la differenza di tempi è t’2 (P’) – t’1 (P’), mentre per il sistema fermo la differenza di tempo è t2(P2) – t1(P1). Ovviamente, per Galileo non cambia niente dato che gli orologi in P1 e in P2 sono sincronizzati tra loro e con quello di P’. Per lui è come se la differenza di tempo fosse stato misurata da uno stesso orologio. Dato che t’ = t, vale anche t’1 = t1 e t’2 = t2. Le due differenze coincidono perfettamente. Noi, però, dobbiamo, invece, tener ben presente questa fondamentale differenza; i tempi di S’ sono misurati da un solo orologio, mentre i tempi di S’, osservato da S, sono misurati da due orologi posti in punti diversi.
Per adesso, comunque, possiamo dire che nella trasformazione galileiana, dove l’unica cosa che capita è uno scorrimento spaziale di un sistema rispetto a un altro, il tempo scorre sempre nello stesso modo in tutti i sistemi di riferimento e -soprattutto- gli orologi del sistema in movimento S’ segnano la stessa ora di quelli fermi di S, se osservati da S. In altre parole le linee di simultaneità rimangono le stesse per qualsiasi sistema.
Utilizziamo il nuovo diagramma spazio temporale di Fig. 4 e descriviamo il moto di E’ del sistema in moto S’ (evento, dato che definiamo un punto spaziale attraverso il tempo in cui viene osservato) nel sistema di riferimento S, considerato fermo. Ho parlato di “moto” dato che , malgrado E’ stia fermo nel suo sistema, esso deve muoversi spazialmente solidalmente con S’. Vediamo cosa capita, utilizzando il diagramma x,t. Ricordiamo un’altra cosa fondamentale: quando eseguiamo questa operazione vuol dire che tracciamo gli spostamenti spazio-temporali degli eventi di S’ nel sistema di riferimento di S. Il che vuol dire che se descrivessimo l’evento E’ di S’ nel suo sistema di riferimento lo vedremmo fermo nello spazio e muoversi solo seguendo il passare del tempo, così come avevamo descritto un evento del sistema S nella Fig. 2.
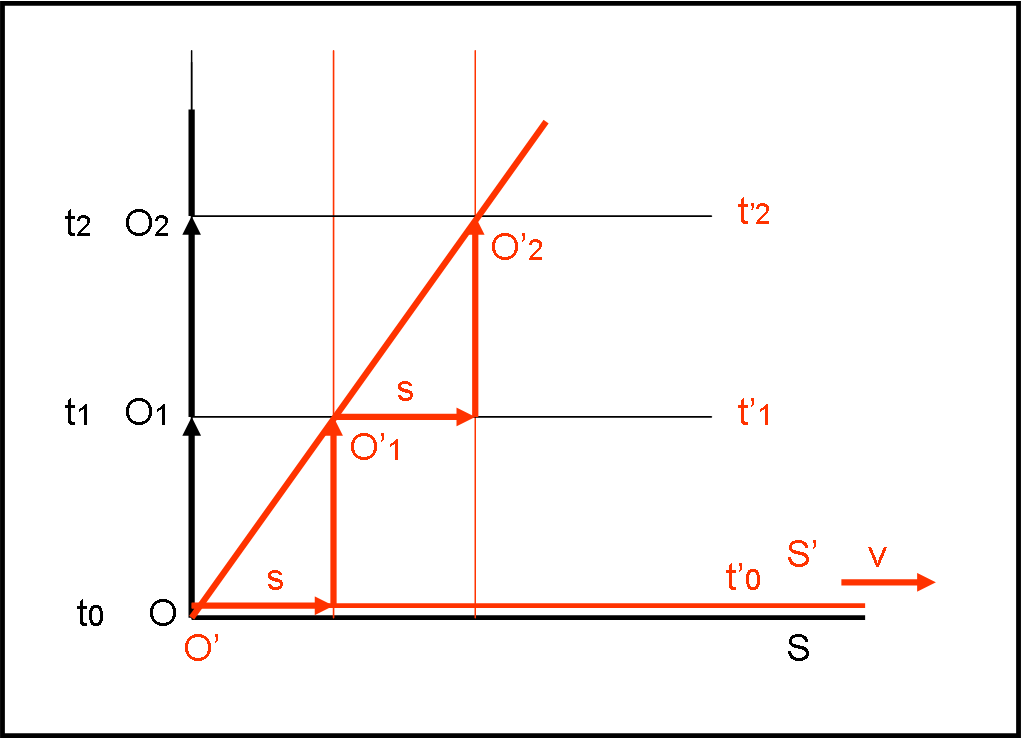
All’istante t0 i due sistemi coincidono. Prendiamo come eventi proprio quelli relativi al punto O’, tanto per semplificare le cose. Abbiamo che, per t = t0, O coincide con O’. All’istante t1, O’ si è spostato in O1’ lungo l’asse delle x di una quantità pari a s = v dt = v (t1 – t0) = v(t’1 – t’0) (non sto a ripetere il significato di velocità relativa). Tuttavia, nell’intervallo dt, sia O che O’ si sono anche “mossi” lungo la retta verticale che identifica il tempo t1 = t’1, arrivando in O1 e O’1. Andiamo avanti e consideriamo il sistema S’ a un tempo t2 = t’2. Solito spostamento lungo l’asse dello spazio e solito spostamento lungo l’asse del tempo. Possiamo concludere facilmente che il moto apparente di O’ rispetto al sistema S non è altro che la retta descritta da O’ (O’ - O’1 – O’2 - …). I “punti” di questa retta sono identificati dal rapporto tra la x e la t dell’evento e quindi hanno come coefficiente angolare proprio la velocità di spostamento spaziale di S’ rispetto a S.
Tuttavia, notiamo una fatto importantissimo: gli assi di riferimento dei due sistemi (x,t) e (x’,t’) rimangono gli stessi. Le linee di simultaneità restano quelle parallele a x = x’ e quelle di immobilità spaziale quelle parallele all’asse t = t’.
Se volessimo dimostrarlo “matematicamente”, la cosa sarebbe immediata. Innanzitutto abbiamo, per definizione, che:
t = t’
Inoltre, sappiamo che:
x’ = x – vt
Il nuovo asse x’ si trova ponendo t = t’ = 0
Ossia:
x’ = x
Mi raccomando, con confondiamo il sistema spaziale x,y a cui siamo abituati con il sistema spazio-temporale x,t che stiamo usando. x è lo spazio e t è il tempo. I punti di questo sistema sono diventati eventi.
Dimostriamo ora, in Fig. 5, che anche le lunghezze si mantengono se sono viste da un altro sistema di riferimento. Sia L’ la lunghezza dell’asta misurata nel sistema S’. Essa è data da x’2 – x’1.
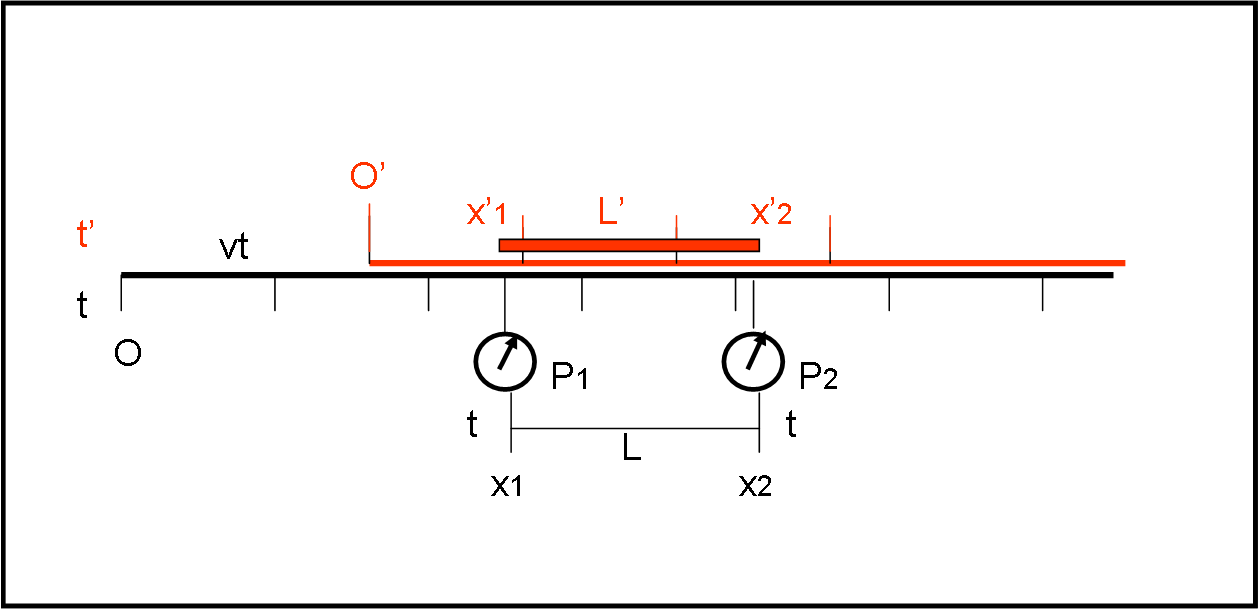
A un certo istante t esistono sicuramente due punti P1(x1) e P2(x2) di S che vedono passare i due estremi dell’asta rigida. Dato che il tempo è lo stesso per entrambi ed è anche lo stesso di S’, possiamo scrivere (utilizzando la trasformazione di Galileo) che:
x’1 = x1 - vt
x’2 = x2 - vt
Basta fare la differenza tra le due relazioni e si trova che
L’ = x’2 – x’1 = x2 – x1 = L
Le lunghezze galileiane si conservano anche se osservate da un altro sistema di riferimento.
Per misurare la lunghezza L’ non abbiamo avuto bisogno di orologi, dato che abbiamo sistemato tutte le aste rigide che volevamo nel sistema di riferimento. In S, invece, per misurare un’asta che appartiene a un altro sistema abbiamo, nuovamente, avuto bisogno di utilizzare due orologi.
La necessità di usare sempre due orologi per misurare sia tempi che distanze di un altro sistema diventerà uno dei punti essenziali della RR.
Tutto ciò che abbiamo dimostrato attraverso aste e orologi vari, si può verificare immediatamente attraverso un grafico spazio-temporale come quello della Fig. 4. Esso ci dice facilmente che si conservano sia le differenze di tempo che le lunghezze, dato che gli assi non vengono alterati. Questo tipo di diagramma è fondamentale per sintetizzare tutte le informazioni relative al passaggio da un sistema S a uno S' in movimento rispetto al primo. Esso permette anche di ricavare come un qualcosa di S' viene vista da S. Per il diagramma galileiano tutto risulta ovvio, ma l'utilità del diagramma diventa ancora più lampante quando le cose si complicano, come nel diagramma di Minkowski.
Concludiamo questo articolo dall’apparenza “stupida” e ripetitiva, dicendo che nella trasformazione galileiana gli orologi vanno sempre d’accordo sia se osservati da un sistema di riferimento sia se osservati da un altro sistema che si muove di moto uniforme. Il che ci fa anche dire che se un evento capita all’istante t in un sistema S, esso è simultaneo con tutti quelli che capitano in altri sistemi, anche in movimento, allo stesso tempo t . La linea di simultaneità è, quindi, qualsiasi retta parallela all’asse dello spazio x. Ossia essa è identificata da t = t’ = cost.
Ne consegue che gli intervalli di tempo si conservano passando da un sistema a un altro e osservando un sistema da un altro. Si conservano, però, anche le lunghezze.
Il tempo e la lunghezza sono assolute e valgono in ogni sistema. L’unica cosa che cambia è lo spostamento di un “qualcosa” rispetto a due sistemi in movimento. Se un certo sistema si muove di una quantità rispetto a un sistema S1, esso si muove di un’altra quantità rispetto a un altro sistema S2, in moto rispetto a S1. Cambia lo spazio percorso ed esso è decisamente relativo al sistema di riferimento usato. Ma ciò è stato spiegato con tutti i dettagli possibili nel capitolo sulla relatività galileiana.
Quanto detto in questo articolo sfiora le più ovvie delle ovvietà, ma è fondamentale soprattutto per comprendere appieno il significato di relatività di simultaneità, la vera base di tutta la RR. Per Galileo è assoluta, ma non per Einstein. Tutta colpa della velocità della luce e della sua lentezza…
Nel prossimo articolo di RRR vediamo di affrontarla senza alcuna pietà!






11 commenti
Ciao Enzo, premetto di non aver ancora letto questo articolo, ma va integrato al "Le basi della Relatività Ristretta o Speciale " oppure se si è compreso quello si può anche saltare?
caro SMA,
sì, è solo una ricerca di miglioramento esplicativo, ma non dice niente di più... Sto scrivendo questi spezzoni solo per cercare di aiutare chi ha ancora dei dubbi. In qualche modo, cerco di seguire le indicazioni che mi aveva dato Simone...
Penso di scriverne ancora uno sul concetto di simultaneità e poi vedere se arrivano nuove richieste di approfondimento. In caso contrario, continuerò con lo spazio di Minkowski...
Ti ringrazio, sei stato veramente fantastico.
Hai messo veramente i puntini sulle i.
Aspetto con impazienza il prossimo articolo sulla simultaneità.
P.S. Per contribuire alla causa ho comprato tutti e 4 i tuoi libri, dovrebbero arrivare a breve.
Ciao
doppio grazie Simone!!!!
Caro Enzo, questi articoli offrono sempre l’occasione di ripassare e/o comprendere meglio l’approccio con la RR.
Volevo segnalarti un piccolo refuso, sotto la figura 1 si fa riferimento all’asta rigida L’, posta tra P’ e Q’…… forse intendevi tra P’ e O’.
Consentimi solo una piccola considerazione a proposito della “linea di immobilità spaziale” (nell’ultimo articolo su Minkowski nei miei appunti l’avevo definita linea di simultaneità spaziale).
Tale linea, corrisponde a rette parallele all’asse T’ ed indica un “evento” fermo per il sistema S’ (così come le linee di simultaneità temporale sono quelle parallele all’asse x’).
Nella relatività Galileiana essendo T=T’, ciò che è fermo (nello spazio) per S’ lo è anche per S, ma quando si passa alla RR (ossia se le velocità tra S e S’ sono relativistiche), ciò che è spazialmente fermo per S’ (rette parallele all’asse T’) non lo è per S (rette parallele all’asse T) e viceversa.
Sbaglio?
Paolo
caro Paolo,
no, non è un refuso... ho considerato un punto Q' qualsiasi che si comporti come P', senza inserirlo nella figura. Però, hai ragione tu... tanto valeva considerare O' come estremo dell'asta.
La parte dopo mi lascia un po' interdetto (ma non vorrei aver capito male io). Ciò che è fermo nel sistema S' può benissimo muoversi nel sistema S. Ciò deriva dal fatto che S' si muove, traslando, lungo l'asse x. Infatti. x = x' + vt. Tutti i suoi punti si muovono di conserva rispetto a S. Tuttavia, anche se non si conserva lo spazio si conserva il tempo. Essere T = T' vuol solo dire che eventi che si manifestano in sistemi diversi (e che quindi cambiano la loro posizione relativa) mantengono comunque lo stesso tempo. Una retta parallela a x individua comunque per loro la simultaneità. Un punto di S' si muove solo lungo la linea del tempo rispetto al suo sistema (dato che è fermo), ma si muove anche lungo x rispetto a S. Ne viene fuori il moto descritto dalla trasformazione x = x' + vt o, analogamente) x = x' + vt'.
O intendevi qualcos'altro?
caro paolo,
quello che ho scritto è in pratica la Fig. 4.
Enzo hai ragione ad essere interdetto, avevo in testa un concetto ma ciò che ho espresso è un'altra cosa, ossia ho detto una sciocchezza .
.
Provo perciò a spiegarmi meglio.
Prendo in considerazione due “punti” spazialmente fissi del sistema S' in movimento.
Per S' questi due “punti” si muovono solo nel tempo, per cui la loro distanza non cambia.
Per S questi due punti si muovono entrambi di un certo spazio in un intervallo di tempo (ossia con una certa velocità costante).
Nel sistema Galieliano T=T', per cui le rette parallele all'asse T' sono le stesse parallele all'asse T.
L'asse delle ordinate T', visto da S, si muove in solido con il sistema S', per cui entrambi i punti di S' si allontanano alla medesima velocità e la loro distanza vista da S non cambia (x1= x'1 +vt ed x2=x'2 +vt).
Se S' si allontana da S a velocità relativistiche, l'asse T' ha un'inclinazione diversa dall'asse T, per cui le rette parallele a T sono diverse da quelle parallele a T'.
Ne segue che per S' la distanza tra i due punti non cambia (variando il tempo T', i due punti mantengono la stessa distanza, poiché i punti fermi per S' giacciono su due rette parallele a T').
Per S, invece, la distanza tra i due punti varia poiché per il sistema fermo S le rette parallele a T sono diverse da quelle parallele a T' .
In pratica i due eventi (termine più appropriato di punti) spazialmente fermi in S' si spostano nel tempo lungo due rette parallele a T', mentre il sistema fisso S legge il tempo con rette parallele all'asse T, quindi la distanza spaziale tra i due eventi, letta usando rette parallele all'asse T, risolta diversa, ossia la misura della distanza spaziale tra i due eventi non è la stessa di quella misurata da S' (contrazione lunghezze).
Lo stesso identico discorso si potrebbe fare prendendo in considerazione due eventi spazialmente fermi per S, poiché in tal caso la distanza tra questi due eventi misurata da S' con rette diverse da quelle parallele all'asse T, apparirebbe contratta (cambia solo il segno di v).
Forse così va meglio.
Paolo
direi proprio di sì Paolo!
 E soprattutto quando riusciremo a descrivere il paradosso dei gemelli sia dal punto di vista di chi viaggia che di chi sta fermo e verrà fuori che anche con la sola RR tutti e due arrivano a dire che chi viaggia invecchia di meno! Un esercizio veramente illuminante (che però ha bisogno prima della composizione relativistica della velocità...) che penso proprio ti entusiasmi!
E soprattutto quando riusciremo a descrivere il paradosso dei gemelli sia dal punto di vista di chi viaggia che di chi sta fermo e verrà fuori che anche con la sola RR tutti e due arrivano a dire che chi viaggia invecchia di meno! Un esercizio veramente illuminante (che però ha bisogno prima della composizione relativistica della velocità...) che penso proprio ti entusiasmi!
Vedrai come ti divertirai con Minkowski...
Se riesco a stare un po' tranquillo, spero di arrivarci in fretta...
In pratica la "linea di immobilità spaziale" sarebbe la cosiddetta "linea di Universo" di un oggetto fermo?
esattamente SMA. Ma l'ho chiamata io così, solo per cercare di introdurre meglio e più semplicemente l'argomento (parlare subito di linea di Universo, poteva forse creare un po' di spavento... a un livello così iniziale ed elementare).