Categorie: Relatività
Tags: cono di luce entanglement eventi futuro invariante relativistico Minkowski passato presente relatività ristretta relatività speciale Universo degli Eventi
Scritto da: Vincenzo Zappalà
Commenti:22
Il diagramma di Minkowski. 7: l’Universo degli Eventi **
Il diagramma di Minkowski dice molto di più di quanto siamo riusciti a descrivere finora. In qualche modo, ci siamo limitati a vedere graficamente come si possono ottenere le più importanti conseguenze della RR: dilatazione dei tempi e contrazione delle lunghezze. Siamo riusciti in tutto ciò introducendo una quantità fondamentale e assoluta: l’invariante spaziotemporale s2, che rimane sempre uguale a se stesso pur cambiando sistema di riferimento.
E’ proprio questa specie di “distanza” che ci ha permesso di tracciare facilmente le iperboli di calibrazione. Un ruolo altrettanto fondamentale nella descrizione grafica della RR viene giocata dal concetto di relatività della simultaneità. Essa è legata strettamente al numero di orologi che si devono usare. Se ne usiamo uno solo stiamo utilizzando il tempo proprio che coincide con l’invariante spaziotemporale. Non per niente, avevamo posto questo invariante uguale a 1 o a -1 per ottenere le curve di calibrazione che ci regalavano il luogo dei punti che al variare del sistema di riferimento indicavano l’unità di misura. Ci eravamo accorti che il tempo proprio è sempre visto scorrere più lentamente da un sistema considerato fermo, da cui seguiva, appunto, la dilatazione dei tempi.
Tutti questi concetti vanno compresi e incasellati bene nella propria mente per gustare al meglio la semplicità e le finezze dell’intera teoria e della sua applicazione geometrica nel diagramma di Minkowski. Un diagramma che assomiglia (per i più anziani) alle tasche di Eta Beta, amico alieno di Topolino, dalle cui piccole tasche usciva sempre di tutto e di più. Invito, perciò, tutti gli interessati a leggere e/o rileggere attentamente tutti i capitoli precedenti, cercando di eliminare ogni dubbio. Cercherò di mettere tutto assieme, includendo anche le parti aggiunte per ulteriore approfondimento e i quiz di preparazione.
La parte che conclude la seconda sezione della RR è, in realtà, la più semplice e intuitiva tra tutte, anche se ha già in sé le ricadute più importanti da un punto di vista fisico. Essa ci porta all’interno dell’Universo degli Eventi, dove ogni evento acquista la sua vera essenza nel contesto dell’intero universo, sia esso passato, presente e futuro. Ci illuderà anche, per un attimo, di poter viaggiare indietro nel tempo, ma sarà solo un attimo, perché ci accorgeremo subito che certe situazioni sono vietate dalla Natura e dalle leggi della RR.
Ancora simultaneità relativa
Come già ribadito, Il diagramma di Minkowski permette di comprendere in modo molto diretto tutti i fenomeni descritti in precedenza. Richiamiamo ancora una volta, ad esempio, come sia immediato il fatto che eventi simultanei in un dato riferimento non lo siano più in un diverso riferimento. Un concetto che deve essere compreso completamente e che si ricollega perfettamente al numero di orologi che si devono usare. Ricordiamo ancora che il tempo proprio è il tempo che si misura con un solo orologio, solidale con il moto del sistema di riferimento. Illustriamo, ancora, questi concetti nella Fig.re 1 e 2.
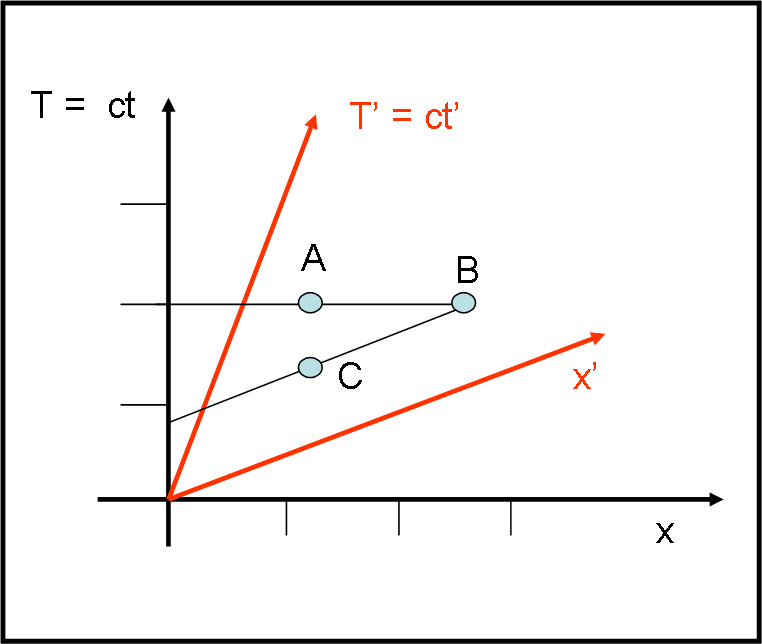
Nella Fig. 1 vediamo immediatamente che due eventi (A e B) simultanei nel sistema (x,T) non lo sono più nel sistema (x’, T’). D’altra parte, gli eventi C e B sono simultanei nel sistema (x’,T’), ma non lo sono più nel sistema (x,T).
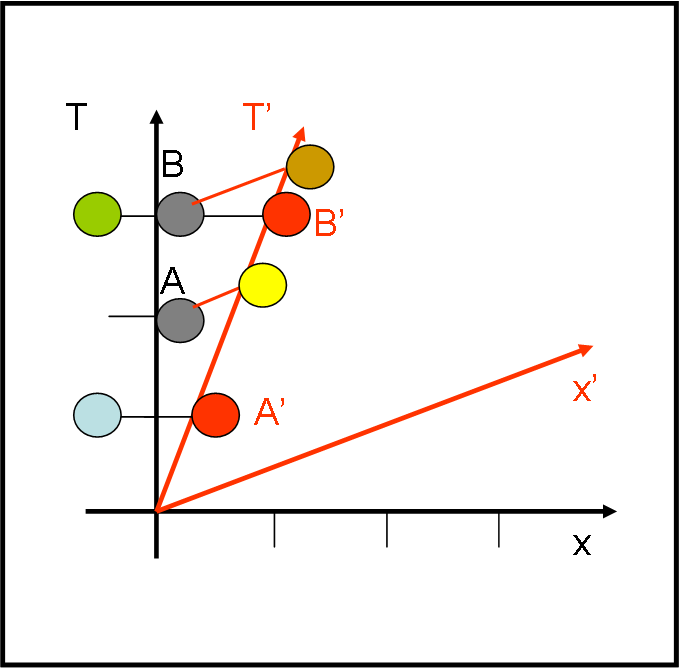
Nella Fig, 2 consideriamo il moto di un oggetto nel sistema (x’,T’). Esso utilizza solo l’orologio rosso per misurare il suo tempo (tempo proprio). Quando capitano gli eventi A’ e B’, il sistema (x,T) è costretto a misurarli con due orologi diversi (azzurro e verde). Analogamente, quando un oggetto si muove nel sistema (x,T), utilizza il solo orologio grigio per misurare il tempo dei vari eventi, come A e B. Il sistema (x’,T’) deve invece utilizzare due orologi (giallo e marrone).
Sono cose che abbiamo già visto e rivisto, ma vale la pena richiamarle ancora una volta, per essere pronti al nuovo salto concettuale.
L’Universo degli Eventi
Iniziamo attraverso un approccio “formale” che si riferisce soltanto all’invariante spaziotemporale. Riscriviamo ancora la formula che lo definisce:
s2 = T’2 = T2 – x2
Essa ci dice che l’invariante non è altro che il tempo proprio di un sistema che usa un solo orologio. Rappresentiamo quando detto nella Fig. 3.
Consideriamo la situazione in cui s2 > 0. Cosa vuol dire questa condizione? Introduciamo i valori assoluti delle due quantità T e x (abbiamo considerato l’inizio degli intervalli invarianti coincidente con l’origine degli assi; altrimenti avremmo dovuto considerare delle differenze di x e di T).
Affinché l’invariante sia positivo è necessario che:
|T| > |x|
E’ stato necessario introdurre il valore assoluto perché altrimenti avremmo potuto avere T positivo e x negativo e sarebbe stato, comunque, T > x, ma, eseguendo il quadrato avremmo potuto ottenere s2 = T2 – x2 < 0. Infatti, poniamo T = 3 e x = - 5. Avremmo:
32 – 52 = 9 – 25 = -16.
L’uso dei valori assoluti ci garantisce che se |T| > |x| deve anche essere T2 – x2 > 0. Tuttavia, se:
|T| > |x|
Segue che:
|x|/|T| < 1
Ossia:
v < 1 = c
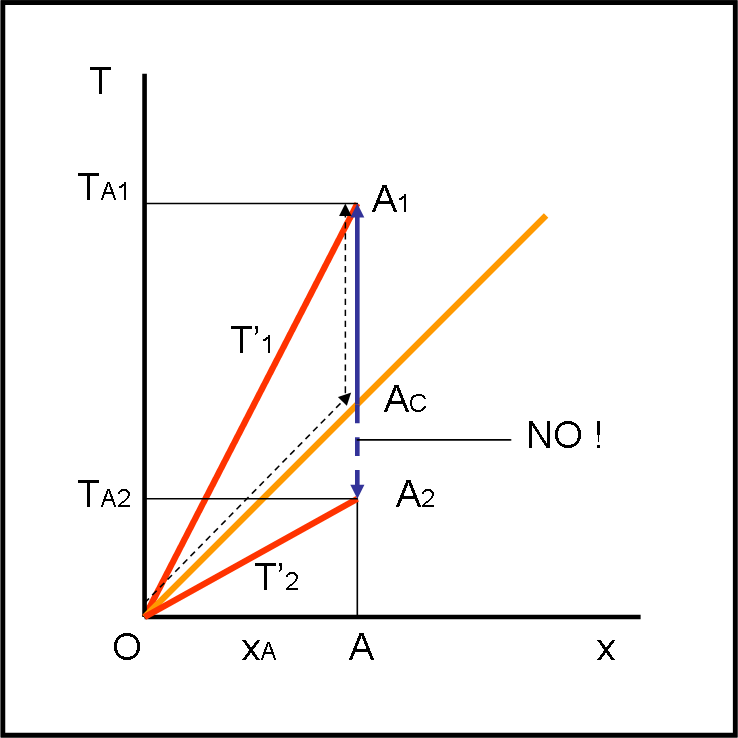
Siamo nelle condizione dell’evento A1 con T = TA1 e x = xA = xA1
Attenzione a quello che dico: “La distanza spaziale (xA1) tra i due eventi O e A1 è sufficientemente piccola perché l’informazione mandata da O possa sempre raggiungere A prima che A1 avvenga”.
Non spaventatevi, mi spiego meglio (anche se non sembra, ho detto una vera banalità…). E’ sempre possibile inviare un’informazione luminosa tale che tocchi la verticale, passante per A e A1, in AC, con AC che precede temporalmente l’evento A1.
Cosa succede, in pratica, per gli eventi di tipo A1 (ossia quelli per cui s2 > 0)? Possiamo inviare un segnale luminoso (ossia un’informazione) seguendo la retta che indica la velocità della luce fino a incontrare il punto A che si sta muovendo soltanto lungo il tempo (ossia è immobile spazialmente nella sua linea di universo). Lo incontra in AC. C’è ancora tutto il tempo che si vuole prima che avvenga l’evento A1. Siamo arrivati in anticipo e siamo sicuri che la nostra informazione luminosa raggiunga A prima che per A si verifichi l’evento A1.
Ho raccontato questa piccola “avventura” in un modo che difficilmente si incontra nei testi, sperando di rendere il concetto della zona in cui s2 è maggiore di zero ancora più chiara di quello che è. La situazione può essere espressa in modo molto più sintetico e formalmente corretto: per ogni evento di tipo A1 esiste sempre un sistema di riferimento tale che O e A1 siano eventi legati causalmente. In altra parole, per una certa velocità AMMISSIBILE (inferiore a c), O e A1 rappresentano due eventi “subiti” dallo stesso punto. O, se preferite , è sempre possibile legare i due eventi attraverso un solo “oggetto” che misuri il tempo con un solo orologio.
Possiamo facilmente limitare questa zona molto “reale”. Essa è ovviamente confinata dalla condizione:
|T| = |x|
Ossia
s2 = 0
e ancora:
|x|/|T| = c = 1
Questa è proprio la linea che descrive la traiettoria spaziotemporale della luce.
La parte di spaziotempo di Minkowski compreso tra le rette T = x e T = - x rappresenta il luogo di tutti gli eventi che possono essere connessi al punto O. In poche parole rappresentano il suo FUTURO assoluto. Tutte le linee che vanno da O verso eventi interni a questa zona rappresentano il possibile futuro di O. Queste linee sono le ben note LINEE DI UNIVERSO. Prolungando le rette della luce verso la parte inferiore otteniamo una zona simmetrica rispetto all’asse x. Questa zona rappresenta il PASSATO assoluto di O. In altre parole, ogni possibile evento del passato che può essere collegato ad O (all’istante T = x = 0).
Conviene riassumere quanto trovato finora. Dato un evento O e un evento A1 che appartenga alle zone appena definite, è sempre possibile trovare un sistema di riferimento inerziale in cui gli eventi O e A1 avvengono nello stesso luogo e sono distanziati solo nel tempo. Nella zona superiore l’evento A1 segue SEMPRE l’evento O, qualsiasi sia la sua posizione. La regione così individuata rappresenta il futuro di O. Nella zona inferiore l’evento A1 precede SEMPRE l’evento O e siamo nel passato di O.
Fermiamoci un attimo a riflettere. Non abbiamo fatto altro che introdurre il cono di luce di O. Tuttavia, ci siamo già accorti che il diagramma di Minkowski ha permesso di rappresentare in una sola figura TUTTO ciò che può aver causato O e che potrà essere causato da O.
Ritornando all’invariate spaziotemporale, possiamo chiamare ogni intervallo tra O e un qualsiasi altro evento contenuto nelle due zone appena descritte come intervalli di tipo tempo. Il nome deriva dal fatto che ogni intervallo di questo tipo può essere descritto da un solo punto con un solo orologio (esiste sempre un sistema di riferimento che abbia OA1 come asse T’).
Le due linee che corrispondono al valore zero dell’invariante sono le linee relative alla luce e gli intervalli che si misurano su di loro si chiamano intervalli di tipo luce.
La Fig. 3 ha, però, molto altro da dirci.
Consideriamo la situazione:
s2 < 0
Essa si ottiene quando:
|T| < |x|
Ossia quando:
|x|/|T| = v > 1 = c
Siamo nel caso dell’evento A2. La distanza spaziale tra A2 e O è talmente grande che nessuna informazione può raggiungere A2 prima che l’evento sia avvenuto. Per poterlo fare dovrebbe viaggiare più veloce della luce. Ne segue che l’informazione luminosa incrocia la verticale passante per A, DOPO che l’evento A2 è già avvenuto. Sembra di essere in un film di Antonioni: incomunicabilità, pura incomunicabilità!
Parlando in modo formale: per ogni evento di tipo A2 NON esiste mai un sistema di riferimento tale che O e A2 siano eventi legati causalmente. In altra parole, per una certa velocità AMMISSIBILE, O e A2 rappresentano due eventi del tutto scorrelati.
Tuttavia, è sempre possibile trovare un sistema di riferimento in cui i due eventi siano simultanei (ossia abbiano la stessa x’). Le parti a destra e a sinistra del cono di luce indicano eventi A2 che niente hanno a che fare con O da un punto di vista temporale, dato che l’informazione non riesce a raggiungerne uno partendo dall’altro. Tuttavia, esiste sempre un sistema di riferimento nel quale i due eventi avvengono nello stesso istante.
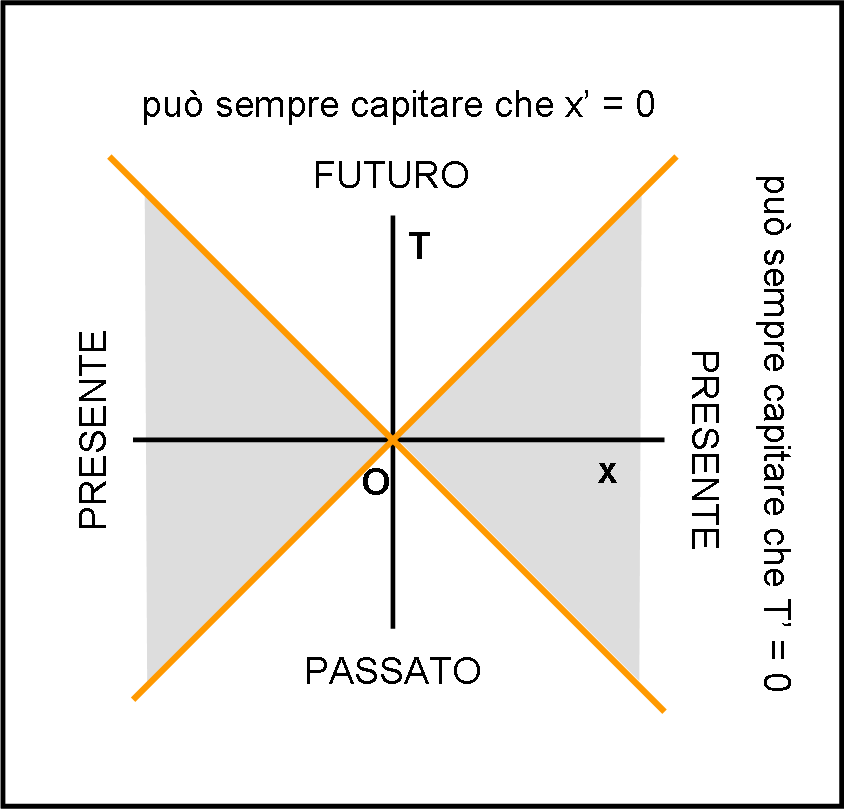
in parole ancora più povere, esse rappresentano il PRESENTE per un certo sistema di riferimento. Le due zone comprese tra le linee di linee (a destra e a sinistra esternamente al cono di luce) possono essere considerate il PRESENTE di O.
Riassumendo:
Per un qualunque punto A2 possiamo tracciare un asse x’ che passi dall’origine O, cioè possiamo trovare un sistema di riferimento inerziale in cui O e A2 avvengono nello stesso tempo e sono distanziati solo nello spazio. Possiamo, cioè, sempre trovare un riferimento inerziale in cui gli eventi O e A2 appaiono simultanei.
Gli intervalli invarianti di queste zone sono chiamate, ovviamente, intervalli di tipo spazio.
Anche la parte del diagramma che sembrava del tutto estranea alla realtà, assume una sua consistenza fisica e reale, dato che rappresenta tutto ciò che esiste nell’Universo e che mai potrà o può avere avuto contatti causali con O.
In Fig. 4 rappresentiamo, ancora una volta, i vari tipi di intervalli spaziotemporali e i relativi sistemi di riferimento.

In Fig. 5 riassumiamo l’Universo degli Eventi.
Giochiamo con Minkowski
Tutto l’Universo degli eventi è stato rappresentato nel fantastico diagramma di Minkowski, perfettamente in linea con le leggi della RR. I “giochi” e gli esercizi che si possono compiere con queste semplicissime nozioni, legate strettamente alla definizione dell’invariante spaziotemporale sono innumerevoli e vanno ben al di là della visione statica che appare. Nello stesso digramma si può rappresentare la cinematica, la dinamica e la fisica più generale della RR. Non sarà cosa così ovvia e intuitiva, ma un giorno ci potremo anche provare (per favore, però, se anche volete tentare non pubblicatelo nei commenti e non chiedete pareri nemmeno personali: certe cose si possono ottenere solo con parecchia pazienza, molto ordine e tanta logica. Altrimenti si cade nella solita, tragica, confusione che ben conosciamo).
Vorrei, a questo punto, fare una constatazione molto importante concettualmente. La RR è riuscita a demolire i due principali invarianti della fisica classica: la distanza tra due punti e la distanza tra due eventi nel tempo. Due concetti, che erano considerati assoluti nella meccanica classica, diventano nella RR relativi al sistema di riferimento. Tuttavia, non tutto è relativo (come si usa spesso dire a casaccio…). Innanzitutto non lo è la velocità della luce che è addirittura uno dei punti base di tutta la teoria. E poi ecco comparire l’invariante spaziotemporale, una distanza tutta speciale che risulta costante per tutti i sistemi di riferimento.
Proprio questo invariante ha consentito di interpretare, dal punto di vista matematico, la realtà fisica collocandola in uno spazio a 4 dimensioni entro il quale la distanza tra due eventi viene definita attraverso tale intervallo. Noi ne abbiamo usato solo due, trascurando y e z, ma sarebbe del tutto immediato inserire queste due coordinate. Non lo si fa sia per non creare figure visivamente insostenibili, sia per la “scarsa” importanza che esse assumono, quando il movimento avviene solo lungo x.
Tutto sembrerebbe perfetto. Vi è solo una piccola mancanza di simmetria: il segno diverso che hanno, nell’invariante, la x e la T. Si potrebbe anche eliminare l’asimmetria passando ai numeri complessi e inserire la radice quadrata di -1. Si otterrebbe una formula perfettamente simile a quella del teorema di Pitagora. Tuttavia, per avere un risultato esteticamente migliore (è poi vero?) si complicherebbero tragicamente le cose, dato che introdurre la radice quadrata di -1 può essere fatto con la giusta comprensibilità solo dopo aver introdotto tutta la teoria dei numeri complessi. Preferisco decisamente, come ormai quasi tutta la Scienza ufficiale, lasciare quel segno meno, poco aggraziato, se volete, ma decisamente più comprensibile per una divulgazione efficiente.
Uno strano teorema di Pitagora
Prima di chiudere questa seconda parte della RR, lasciatemi proprio parlare ancora un po’ dell’invariante e della sua “quasi” analogia con il teorema di Pitagora. Così facendo troveremo un risultato a prima vista assurdo, ma che nella geometria non euclidea di Minkowski ci porta immediatamente alla soluzione del paradosso dei gemelli (e ci regala la soluzione del quiz che era stato proposto un po’ di tempo fa).
Richiamiamo ancora una volta il teorema di Pitagora e confrontiamolo con l’invariante spaziotemporale nella Fig. 6. A sinistra abbiamo il nostro spazio (x,y) euclideo e a destra lo spaziotempo (x,T) non euclideo.
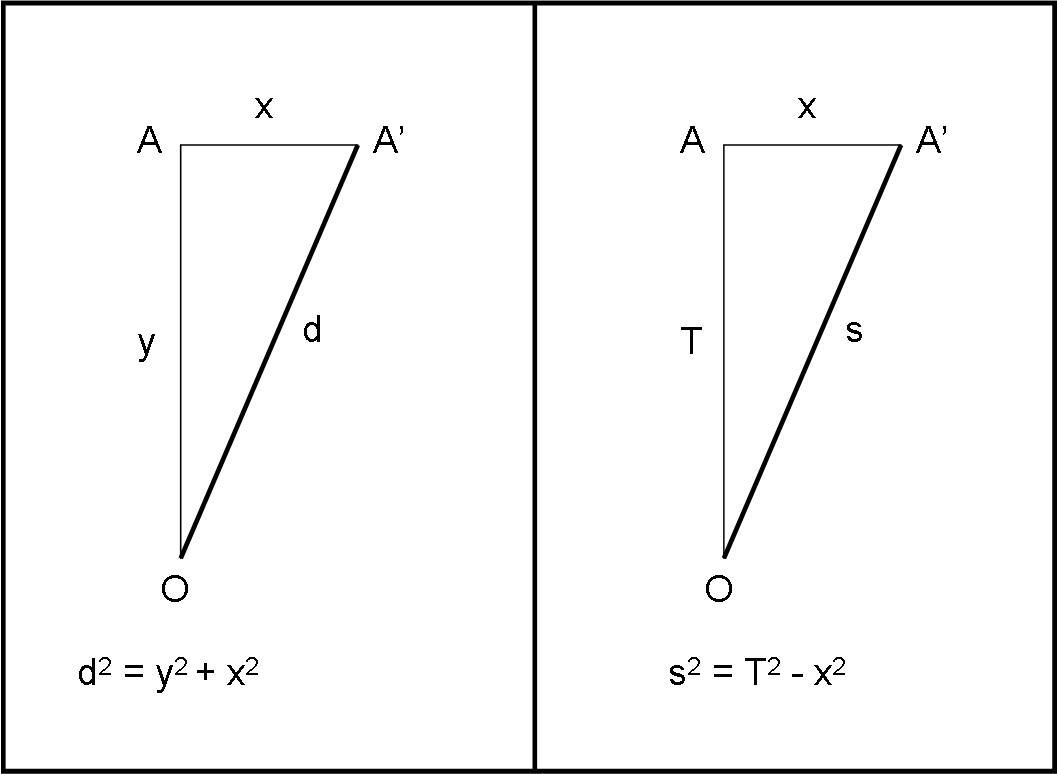
Ricaviamo d dalla prima:
d = (y2 + x2)1/2 = y (1 + (x/y)2)1/2
qualunque sia il rapporto x/y, la somma sotto radice quadrata deve essere maggiore di 1, così come la radice quadrata. Risulta immediatamente che d > y. Beh… lo sapevamo già dalla stessa definizione di Teorema di Pitagora: l’ipotenusa è maggiore dei cateti!
Passiamo allo spaziotempo di destra. Ricaviamo s:
s = (T2 - x2)1/2 = T (1 - (x/T)2)1/2 = T (1 - v2)1/2
Il rapporto tra x e T non è altro, infatti, che la velocità di un oggetto che si muove lungo OA’. Ricordiamo anche che s non è altro che il tempo proprio di questo oggetto (misurato con il suo orologio).
v deve sempre essere minore di 1, da cui segue che la radice quadrata è un numero minore di 1. Si può facilmente concludere che:
s < T …. (1)
In poche parole, l’ipotenusa s dello “strano” triangolo spaziotemporale OAA’ è minore del cateto T, malgrado l’apparenza, dovuta al nostro mondo euclideo, inganni.
Passiamo immediatamente alla Fig. 7 dove abbiamo inserito un triangolo AA’O’ sopra quello precedente.
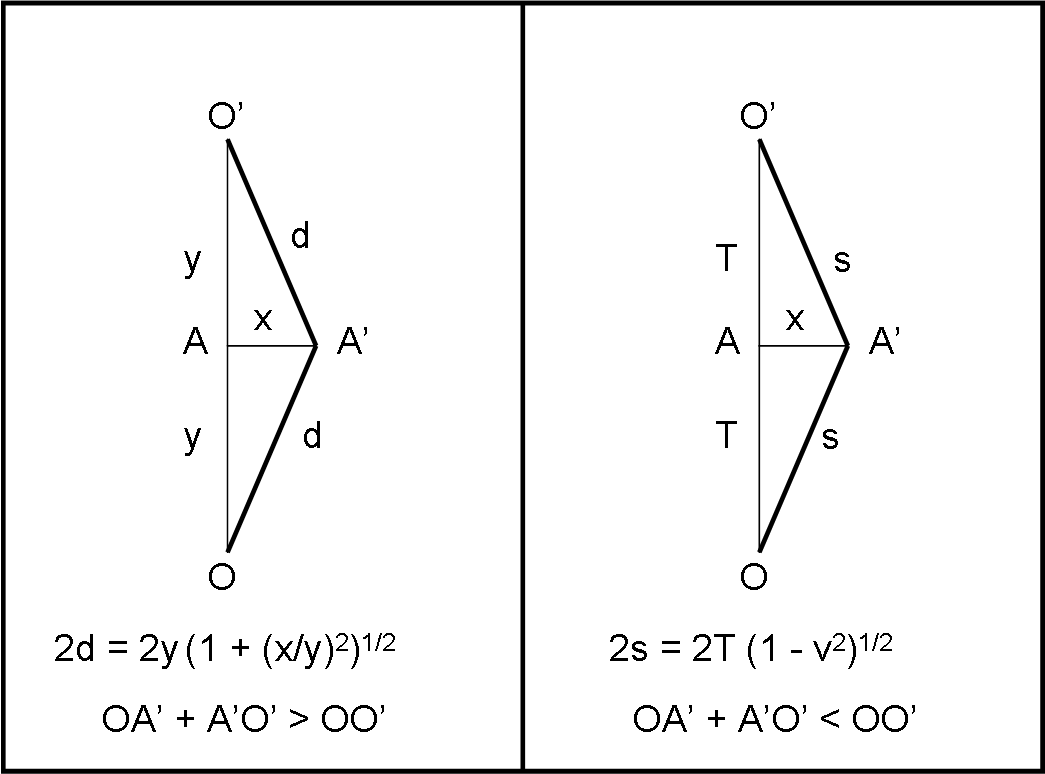
Dalla parte euclidea a sinistra si ottiene immediatamente che:
OA’ + A’O' = 2d = 2y (1 + (x/y)2)1/2
E quindi:
OA’ + A’O' > OO’
Ancora una volta, non possiamo certo stupirci del risultato…
Non dobbiamo, però, nemmeno stupirci di ciò che succede nello spaziotempo, a destra (la velocità cambia di segno, ma non certo il suo quadrato):
OA’ + A’O' = 2s = 2T (1 - v2)1/2
OA’ + A’O' < OO’
Questa apparente assurdità può essere espresso con una proprietà ben più generale: la lunghezza spaziotemporale tra due eventi O e O’ è sempre maggiore di quella di una qualunque altra curva che congiunga i punti O e O’.
In realtà, noi abbiamo dimostrato la proprietà solo per una spezzata formata da due segmenti uguali tra loro. Non è difficile, però, generalizzare quanto abbiamo trovato considerando una qualsiasi linea curva come composta da un numero molto grande di piccoli segmenti. Per ognuno di essi varrebbe la (1). Anche se la velocità cambiano da punto a punto la disuguaglianza è confermata. In pratica, non dovremmo fare altro che sommare la lunghezza di tutti questi trattini rettilinei. Qualcosa del genere:
s = Σ Ti (1 - vi2)1/2
E poi fare tendere a infinito il numero dei trattini. Il simbolo di sommatoria si trasformerebbe in quello di integrale e la curva sarebbe approssimata perfettamente. Quando continueremo con la matematica (prima o poi DEVO farlo) ci potremo anche arrivare in modo ben più accurato.
Per adesso, ci basti aver dimostrato la proprietà attraverso due soli segmenti uguali tra loro: se vale per loro DEVE valere per qualsiasi curva spezzata o continua.
La soluzione del quiz sulla linea più corta e il paradosso dei gemelli
Siamo, quindi, arrivati alla soluzione del QUIZ (QUI). La curva verde è decisamente più corta del segmento rosso. Infatti, il segmento verde AB rappresenta l’invariante relativistico e può essere considerato in un qualsiasi sistema di riferimento, anche in quello in cui il segmento rosso coincide con T verticale. Avremmo la situazione (già ben conosciuta) della Fig. 8.
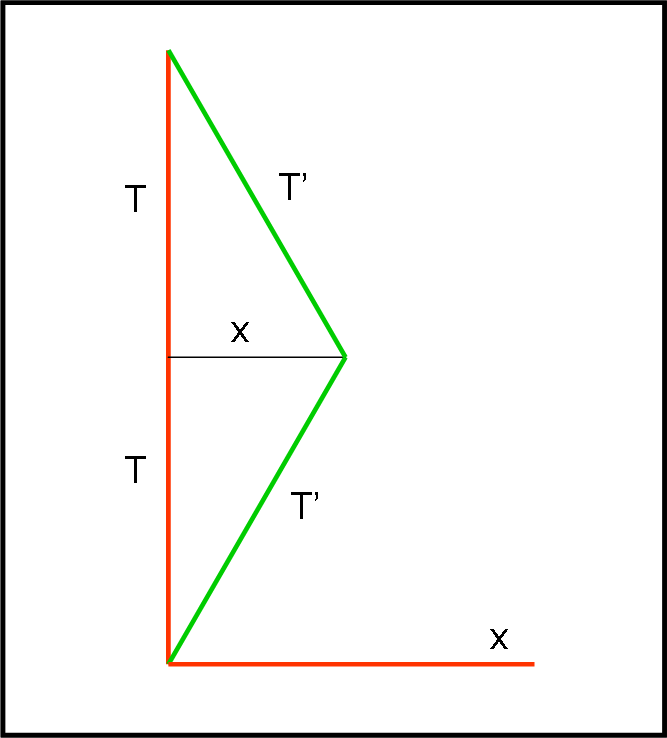
Non ci stupiamo se la linea verde rappresenta perfettamente quella di un astronave che si muove con velocità v fino a una certa distanza spaziale dalla Terra rossa (che si muove verticalmente). Quanto abbiamo appena dimostrato ci dice senza ombra di dubbio che la somma dei due tratti verdi (andata e ritorno) dell’astronave è minore del tratto rettilineo rosso. Ma, su quest’ultimo scorre il tempo proprio della Terra, mentre sulla linea verde scorre quello dell’astronave. Se ne conclude che il tempo dell’astronave scorre più lentamente e l’astronauta è veramente più giovane al suo ritorno a casa. Abbiamo risolto immediatamente il paradosso dei gemelli!
Vale, però, anche l’inverso. Sapendo che l’astronauta rimane più giovane, si può concludere subito che la linea verde è più “corta” di quella rossa!
Si può viaggiare nel tempo con Minkowski?
Il diagramma di Minkowski può anche portarci a viaggi nel tempo? A prima vista sembrerebbe di sì. Consideriamo due eventi A e B simultanei e spazialmente separati nel sistema (x,T). Vediamo come la stessa situazione si presenta in due sistemi (x’,T’) e (x”, T”) caratterizzati da una velocità v uguale e di verso opposto rispetto a (x,T). I sistemi di riferimento risultano, quindi, ruotati in modo simmetrico. Vediamo come si presentano su di loro le coordinate temporali di A e di B. Per trovarle bisogna ovviamente utilizzare gli assi x’ e x”, come ormai sappiamo molto bene. Ci aiuta la Fig. 9.
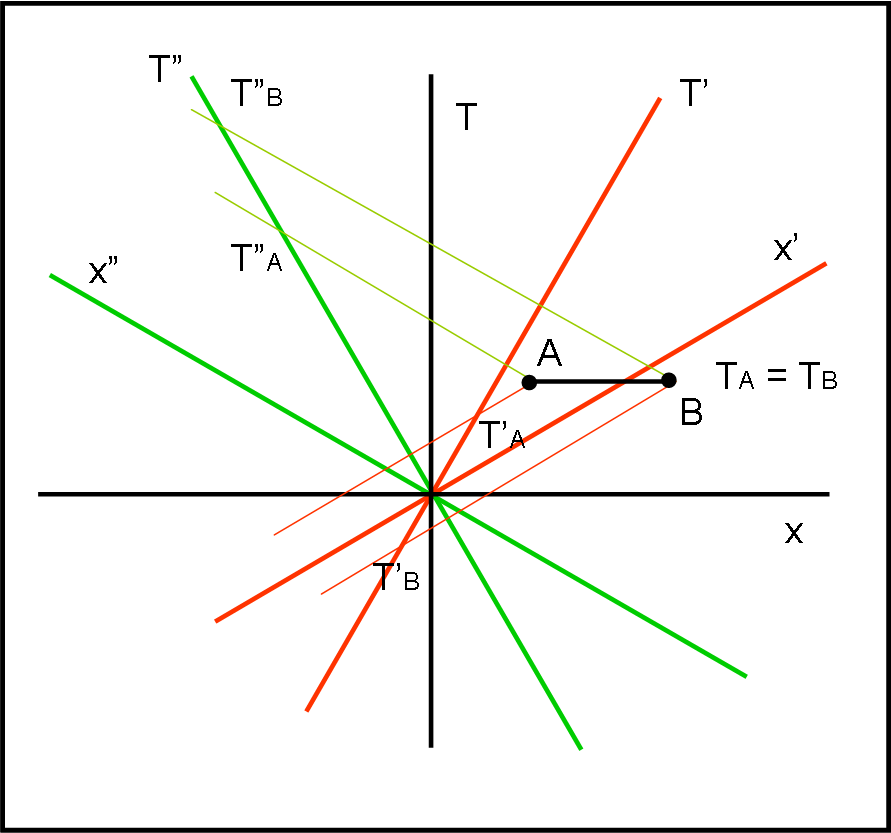
Nel sistema (x’,T’) l’evento A segue l’evento B (gli eventi sono quelli che sono in qualsiasi sistema di riferimento; sono le loro coordinate che cambiano). L’evento A precede, invece, l’evento B nel sistema (x”,T”). Accidenti! Ma allora basterebbe cambiare sistema di riferimento (legati alla velocità) per potere tornare indietro nel tempo e modificare un evento prima che questo accada in un alto sistema di riferimento. No, non illudiamoci, sarebbe troppo bello (?) e facile. Guardiamo meglio l’intervallo spaziotemporale invariante AB. Esso è un intervallo per cui s2 < 0 e, perciò, non può esistere una connessione causale tra A e B. In nessun sistema di riferimento un segnale di luce è in grado di andare da A a B prima che B accada.
Va bene, direi che possiamo fermarci qui. Di materiale per pensare ce n’è molto. Ribadisco ancora una volta la solita preghiera: invece di cercare di complicare ciò che abbiamo imparato, cerchiamo di capire perfettamente ciò che abbiamo imparato. E’ già una conquista non trascurabile… credetemi!
Un periodo di sospensione … relativistica e poi cercheremo di affrontare la dinamica e la fisica della RR, magari usando ancora il diagramma di Minkowski (non ve lo assicuro, però…).
Appendice (piccola e buttata lì…)
Quanto detto finora si riferisce soltanto all’evento O e al suo Universo. Immaginiamo un altro evento O' in Fig. 10.
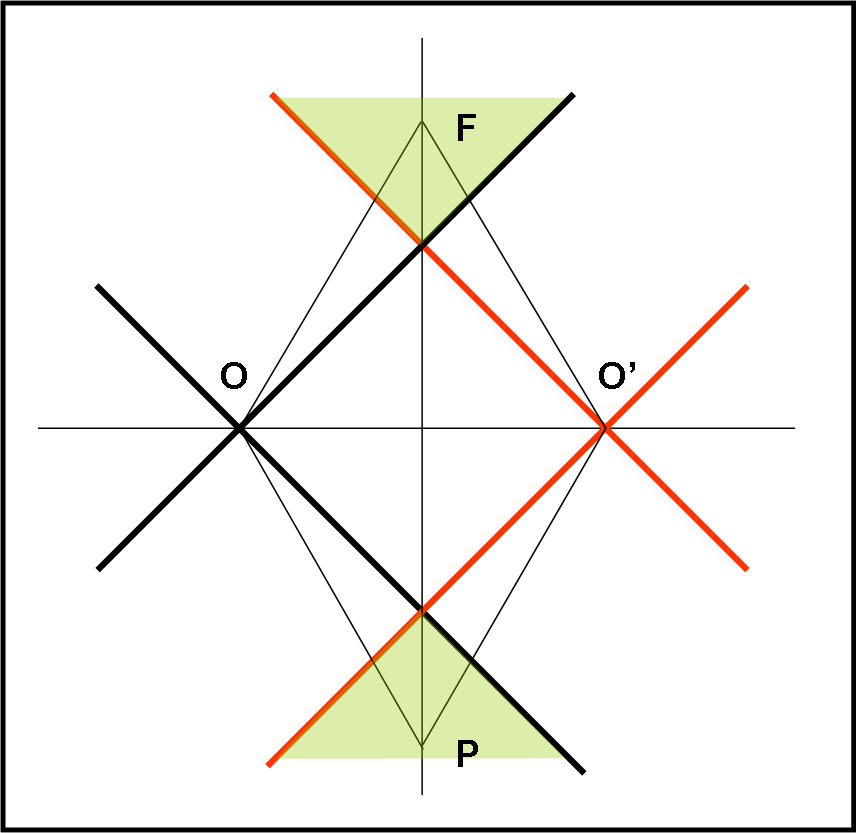
Per quanto detto precedentemente, essi non possono essere legati causalmente. Tuttavia, nel loro passato e nel loro futuro possono avere avuto “contatti”. Basta rappresentare i loro due coni di luce. Essi hanno una parte comune sia nel passato che nel futuro. Ciò vuol dire che nel passato un certo evento P può avere influenzato in qualche modo sia O che O', attualmente del tutto sconnessi. Lo stesso capiterà nel futuro. Eventi come O e O' potranno influenzare un unico evento F. Un certo evento P del passato può benissimo aver dato luogo sia a O che O', mentre un evento F del futuro può essere stato originato sia da O che da O'. L’evento P e l’evento F sono, inoltre, collegati secondo una linea di tipo tempo, ossia la linea di universo PF. Tra le linee di universo che si incontrano partendo da eventi del tutto sconnessi tra loro QUI e ORA vi sono anche le linee di tipo luce, ossia l’informazione… Pensateci un attimo sopra… questa apparente banalità rimanda immediatamente al fenomeno dell’entanglement… F può contenere l’informazione sia di O che di O'. D’altra parte O e O' possono avere, anche se irraggiungibili tra loro, l’informazione di P. Non entriamo, comunque in un argomento che è ben più complesso di quanto possa sembrare. L’accenno serve solo a comprendere quanto sia illuminante un diagramma come quello di Minkowski






22 commenti
commento per garantirmi la email...
Ciao Enzone, come stai? Purtroppo non riesco più a seguirvi come prima ed anche la lettura della RR (e di tutto il resto) va un pò a rilento. Mah ... accontentiamoci di quello che abbiamo.
Ho dato una (purtroppo) rapida occhiata all'articolo che comunque leggerò approfonditamente appena possibile. Ti chiedo una cosa, sperando che non la consideri una inutile complicazione
Parlando di spazi e spazi-tempo piatti (vedi Minkowski) sono sicuro che in più di uno dei nostri amici "circolari" sia sorta spontanea, per associazione d'idee dovuta ad un errato modo d'insegnare la geometria a sQuola (mi dispiace ma la scuola italiana va scritta con la Q) , la convinzione che spazio piatto (riferendosi solo allo spazio) significhi automaticamente euclideo.
Secondo me, a completamento di questa parte di percorso della RR, non starebbe male un articolo in cui spiegare che può esistere uno spazio piatto non euclideo, magari introducendo qualche esempio, senza scendere nei dettagli; insomma, una semplice visulizzazione della questione.
Che ne pensi? So che tu sei un integralista e vuoi (GIUSTAMENTE) affrontare tutti gli argomenti fornendo gli strumenti per comprenderli a fondo. Diciamo allora che questo ipotetico articolo potrebbe essere una piccola e generica introduzione alla geometria non euclidea che tratterai in futuro. Perchè no?
Un caro saluto a TUTTI, perfino a Diego (cosa mi tocca dire!!!)


ciao Alvy!
L'idea mi piace molto (con i giusti tempi esecutivi...). Tuttavia, mi sembra che avessi già scritto qualcosa in passato... ma non sono sicuro. Comunque l'idea è buona ed è da tanto che vorrei parlare di curvatura e di cose del genere... Ogni tanto RICORDAMELO!!!!
Scusa Prof., ho un dubbio riguardo alla spiegazione della figura 9: tu dici che A precede B in (x',T') e A segue B in (x'',T'')... non è, invece, il contrario?
Oppure si tratta solo di un equivoco che nasce da una diversa accezione di "precedere" e "seguire" nel linguaggio comune e in quello matematico?
Comunque, a parte questo dettaglio, il significato della spiegazione è ben chiaro!
P.S.
Appoggio la richiesta di Alvy: anch'io, se penso alle geometria non euclidea (che a sQuola non mi hanno insegnato, nonostante abbia frequentato un liceo scientifico!) tendo istintivamente ad identificarla con ciò che si può "disegnare" sulla superficie interna o esterna di una sfera
scusa Daniela... ma penso sia proprio il modo di considerare il tempo... io ragiono lungo la linea di Universo: tutto ciò che avviene più distante dall'origine verso l'alto lo intendo avvenuto prima. Oggi siamo in O, domani siamo in A e dopodomani in B (lungo t"). L'evento in B precede quello in A. Tuttavia, capisco che dia luogo a fraintendimenti...
Però è anche vero ciò che dici tu, in senso più comune...
Insomma, scegliete voi. L'importante è che i tempi si ribaltino!
OK per la curvatura e per la geometria non euclidea. In qualche modo possiamo dire che lo spazio di Minkowski è quasi-euclideo. Ossia è piatto, ma non vale il teorema di Pitagora. Normalmente si intende per non euclideo uno spazio curvo...
cara Daniela, . Ti do retta e inverto le parole. Mi sa che hai ragione tu nel definire gli eventi solo sulla base del valore del tempo a loro associato... (1 è più piccolo di 2 e quindi precede). Grazie infinite!!!!
. Ti do retta e inverto le parole. Mi sa che hai ragione tu nel definire gli eventi solo sulla base del valore del tempo a loro associato... (1 è più piccolo di 2 e quindi precede). Grazie infinite!!!! 
ci ho ripensato e temo che il mio modo di vedere le cose porti a confusione
Perfetto, grazie!
In realtà il commento "perfetto, grazie" l'avevo scritto dopo il tuo primo commento e prima di leggere il secondo... ci siamo calati così tanto nella RR, che abbiamo ribaltato il tempo anche noi?!

E così il paradosso dei gemelli non è più un paradosso! Enzo, una domanda. Ma se l'evento A è causa dell'evento B posso avere un sistema di riferimento in cui A e B sono simultanei o, addirittura, che B precede A?
caro Gaetano,
guarda la figura 4. Se un evento ha avuto come causa O, ossia O e A sono connessi, esiste sempre un sistema di riferimento in cui O e A sono relativi a uno spesso punto (passa sempre una linea di tipo tempo). Non esiste, invece, nessuna linea di tipo spazio che possa unirli, ossia O e A non possono essere simultanei. Nella zona "spazio" capita il contrario: nessun evento può essere connesso a O, ma può essere, in un sistema, simultaneo con lui. Il fatto che tu consideri due eventi A e B diversi da O, non cambia niente, perché ti sposteresti nell'Universo degli eventi di A e tutto funzionerebbe nello stesso modo. Inoltre, puoi cambiare quanto vuoi il sistema di riferimento sotto cui studiare la situazione, ma s2 è un invariante e quindi niente può cambiare, cambiando sistema da cui vedere le cose.
Il paradosso, in realtà, continua a esistere nella relatività ristretta, mentre sparisce nella generale. Tuttavia, lavorando solo nella ristretta (pur considerando trascurabili gli istanti accelerazione e decelerazione) si può facilmente dimostrare che il viaggiatore DEVE rimanere più giovane. Minkowski lo offre su un piatto d'argento!
Grazie Enzo, anche le domande sbagliate aiutano a capire. Adesso, per me, è più chiara la differenza tra S2 >0, S2<0 e S2=0. Si capisce anche che per un fotone il tempo è fermo essendo S2=0 oppure è una conclusione sbagliata?
dici bene Gaetano. Intendiamoci, però... per il fotone il tempo scorre normalmente, così come lui viaggia alla sua velocità di cui ci rendiamo perfettamente conto. E' il suo tempo che si ferma se visto da un altro sistema. Se avesse un piccolo orologio da polso, lo vedremmo sfrecciare velocissimo ma vedremmo il suo orologio sempre fermo sulla stessa ora.
Le domande non sono mai sbagliate... spesso lo sono le risposte!
Perché il paradosso dei gemelli è ancora in piedi nella relatività ristretta?
mi riferisco alla risposta che ha dato più sopra in questa sezione a Gaetano
"Il paradosso, in realtà, continua a esistere nella relatività ristretta, mentre sparisce nella generale.
Tuttavia, lavorando solo nella ristretta (pur considerando trascurabili gli istanti accelerazione e decelerazione).."
mi sembra che sia stato dimostrato in maniera rigorosa in questo articolo
(a parte il fatto di sostituire la sommatoria con un integrale), e la spezzata con una curva
il moto sulla curva sarebbe poi anche più realistico;
Forse si parla della RG per le accelerazioni che sono equivalenti a un campo gravitazionale,o qualcosa che riguarda
la definizione di sistema inerziale nella RG?
Ma la relatività ristretta non contempla anche i moti accelerati ( tipo il muone nell'anello di accumulazione)?
caro Umberto,
nella RR i sistemi sono inerziali e quindi le accelerazioni non sono contemplate. Ne segue che un cambiamento di velocità nel moto di un corpo non è ammesso in quanto comporterebbe un'accelerazione e/0 decelerazione. Tuttavia, trascurando i momenti di accelerazione e decelerazione (che devono esistere fisicamente), la linea spezzata permette di usare la sola RR per dimostrare che il viaggiatore invecchia di meno. In altre parole, possiamo usare la sola RR per risolvere il paradosso, ma l'aver trascurato il fenomeno che permette il cambiamento di velocità è come se avessimo nascosto la RG sotto al tappeto. Spero di essermi spiegato...
Caro Enzo è un po' che non scrivo....con il caldo che ha fatto mi sono limitato a leggere qualche news.
L'articolo è davvero interessante e suscita diverse riflessioni e qualche dubbio.
Vorrei in particolare soffermarmi sulla figura 5 e sull'area del cono di luce che definisce il presente.
Io la questione la inquadro così.
Due eventi per esser connessi fra loro devono avere avuto (o avranno in futuro) la possibilità di scambiarsi informazioni.
Dato che l'informazione nello spaziotempo non può superare la velocità della luce (i nostri amici fotoni sono i postini più veloci dell'universo), due eventi non possono essere connessi fra loro se sono fuori portata, o meglio se nemmeno la luce ha avuto il tempo di compiere il tragitto che li separa (ovviamente qualunque fenomeno possa legare un evento ad un altro, non può che muoversi a velocità subluminale).
Il dubbio che vorrei esporre è strettamente legato alla definizione di evento.
Se non ho capito male, un evento è caratterizzato da coordinate spaziali e temporali, quindi anche un “punto” immobile nello spazio che si muove solo nel tempo si trasforma in una serie infinita di eventi (sbaglio?).
http://www.astrobin.com/full/34219/B/
Fatta questa breve premessa, vorrei provare ad esporre il problema usando un esempio concreto (una specie di esperimento) ed una figura.
Il fenomeno che si vuole descrivere è una grossa eruzione solare e gli eventi che ne conseguono visti dalla Terra.
Il fenomeno può tranquillamente essere descritto usando un unico sistema di riferimento considerato fermo, quello terrestre (dato che non vi sono in gioco velocità di allontanamento relativistiche tra Terra e Sole), per cui tutti gli orologi sono sincronizzati e misurano lo stesso tempo.
http://www.astrobin.com/full/34219/C/
Nella figura ho indicato in rosso gli eventi che si vogliono prendere in considerazione e solo i coni di luce degli eventi O(1) e S(0).
S(0) è l'evento iniziale, ossia l'eruzione solare e tutti gli orologi misurano Tempo zero (T=0).
La Terra nell'istante in cui avviene l'eruzione si trova nella posizione O (0), per cui nessuno sulla Terra può accorgersi di ciò che sta avvenendo sul Sole, ossia l'evento S(0) non può determinare l'evento O (0).
Non a caso O(0) si trova nella zona del cono di luce presente dell'evento S(0) e viceversa, ossia S(0) che si trova nel cono di luce presente di O(0) (nella figura, per non appesantirla, non ho indicato questo cono di luce).
L'Evento “eruzione solare” S(0) non può essere connesso all'evento O(0).
Ma, dopo circa 8 minuti, la Terra viene raggiunta dalla luce dell'eruzione Solare, per cui si verifica l'evento “avvistamento eruzione solare” indicato con O(1).
L'Evento O(1) è sicuramente connesso all'evento S(0), grazie al fatto che l'informazione dell'eruzione solare è arrivata a noi trasportata dai fotoni, alla velocità della luce, sul bordo del cono di luce di S(0).
Non tutto però viaggia alla velocità della luce, per cui dopo un certo tempo la Terra viene colpita da particelle altamente energetiche prodotte durante l'eruzione solare, che mandano Ko per un po' di tempo diversi satelliti artificiali e producono splendide aurore.
Tale evento nella figura è stato indicato come O(2).
Anche l'evento O(2) è certamente connesso con S(0) e non a caso si trova nella zona che rappresenta il futuro del cono di luce di S(0).
E' corretta una simile rappresentazione?
Il post è già lungo così per cui mi riservo una piccola considerazione sulla figura 10...
Paolo
PS: Piccolo refuso, dopo la figura 7, quando indichi la formula per descrivere cosa succede nello spaziotempo, il quadrato della velocità andrebbe sottratto e non sommato, come riportato correttamente nella figura 7, altrimenti s diventa maggiore di T.
In attesa che Enzo torni dalle meritate vacanze , ne approfitto per postare anche la riflessione che riguarda la figura 10.
, ne approfitto per postare anche la riflessione che riguarda la figura 10. 
Facciamo finta che:
L'evento P rappresenta la partenza di due astronavi, che viaggiano alla stessa velocità costante, in direzione uguale ma con verso opposto (le sottili linee nere rappresentano il loro asse del tempo);
Gli eventi O e O' il cambio di verso delle velocità delle due astronavi (dopo aver percorso la stessa distanza spaziotemporale) che tornano verso il punto di partenza;
L'evento F il ritorno contestuale delle due astronavi al punto di partenza.
Quando le due astronavi si trovano in O e O' non possono in alcun modo comunicare istantaneamente tra loro (O ed O' sono eventi sconnessi fra loro), ma la loro posizione è comunque un effetto dell'evento P (partenza delle astronavi).
Lo stesso ragionamento si può fare per l'evento F e per l'identico viaggio di ritorno.
Ora, facciamo finta che si tratti di eventi naturali e non artificiali (e quindi “manipolabili”), sicuramente l'evento F è il risultato (connesso) dell'evento P, passando per gli eventi O ed O'......
A me sembra, però, che ci siano almeno due modi diversi per “interpretare” un diagramma come quello rappresentato nella figura 10:
il primo è deterministico, ossia P è la causa di O e di O' ed infine di F, il verso del tempo è uno solo, ne segue che F non può determinare P;
il secondo (che preferisco) è probabilistico, un po' come se “coesistessero” infinite possibilità (sovrapposizione di stati) degli eventi iniziali P e finali F di trovarsi in una determinata posizione (purché siano all'interno del cono di luce), ma solo quando F si verifica (viene “osservato”) tutte le altre possibilità si annullano (l'onda di probabilità collassa) e contestualmente si verificano (si può risalire) anche alle posizioni di O; O' e P (tra le infinite posizioni possibili).
Se non ho capito male il tuo richiamo al fenomeno dell’entanglement va inteso che gli eventi O ed O', che potrebbero pure rappresentare il comportamento di due particelle (per esempio il senso di rotazione), pur essendo non connessi tra loro, potrebbero derivare dall'evento F, che potrebbe rappresentare l'interazione “iniziale” tra le due particelle divenute poi O ed O'... o sbaglio?
In ultimo, se la teoria del Big Bang ha qualche fondamento, vi è stato un evento iniziale che è connesso a qualunque evento dell'universo osservabile (eh si anche l'universo ha il suo cono di luce e l'informazione deve poterci raggiungere), un istante in cui tutto era “correlato”, un evento P universale.... forse proprio per questo l'universo appare omogeneo e isotropo e le costanti universali non hanno valenza locale, ma generale.
Mi fermo qui poiché ci vorrebbero ben altre basi per approfondire il ragionamento.
Preferisco attendere i nuovi articoli che hai promesso per ragionare seriamente su CPT (simmetria: inversione di carica, specularità; inversione temporale), inversione del tempo (in parte accennato negli articoli finali sulla QED), mare di Dirac, necessità o meno dell'inflazione e correlazione quantistica.
Paolo
Paolo, solo una piccola considerazione, aspettando Enzo.
Non penso che a livello macroscopico si possa utilizzare la funzione d'onda così come non si può utilizzare la Relatività Ristretta e Generale a dimensioni infinitesimali. Quello di Enzo a me è sembrato solo un complimento al Diagramma di Minkowski.
caro Paolo,
prima di tutto, grazie per il refuso... figurati se non sbagliavo qualcosa...
La tua considerazione è esatta! D'altra parte, vedila così: Tutti gli eventi di O che stanno nel suo futuro, dopo O1, devono essere connessi con S0 dato che stanno all'interno del suo cono di luce futuro. Tutto lì. Gli eventi precedenti O1 non sono connessi fino a che non si vada indietro nel tempo ed si entri nel cono di luce passato di S0. In questo caso, però, sarà S0 che riceve segnali da O (come facciamo noi dalle stelle e dalle galassie o da segnali di fumo di altri mondi... ).
).
caro Paolo,
i tuoi ragionamenti sono essenzialmente giusti. Tuttavia gli eventi F e P, indipendentemente dalla loro storia sono ovviamente connessi e quindi F segue P (P diventerà F anche senza avere alcuna velocità). In questo senso rappresentano un approccio deterministico. Dici bene, però, che F può derivare da P attraverso infiniti modi. Però, non mi sentirei di dire che F da solo fa collassare tutti questi modi, dato che sono tutti plausibili e deterministici. Il passaggio da O, però, fa sicuramente collassare le altre possibilità... o, meglio, le esclude... Un po' diverso è se ci riferiamo solo a oggetti che si muovono alla velocità della luce. In tal caso l'unico modo per P di arrivare in F è passare per O o O'. E un po' come la doppia fenditura...
L'ultima parte è invece perfetta. Due fotoni che provengono da P sono oggi del tutto sconnessi (ossia si trovano a distanze tali che nemmeno la luce potrebbe mandare segnali reciproci), ma sono nati entrambi da P e quindi potrebbero essere proprio le particelle entangled.
Mi sembra anche più che giusto il ragionamento sul Big Bang: il suo cono di luce deve contenere il tutto dato che niente può essere stato sconnesso all'istante t= 0. Tuttavia, questo non dovrebbe implicare una perfetta anisotropia, dato che potrebbe aver mandato cavoli e patate in direzioni diverse. Direi che potremmo dire che i cavoli sarebbero entanglati con i cavoli e le patate con le patate. Tuttavia, c'è del vero comunque, dato che le particelle ultra elementari sono partite tutte assieme ed erano sicuramente entanglate... Insomma, posso dirti che ancora oggi e a livello ultra professionale si discute su questo tipo di visione, senza avere ancora raggiunto un risultato concettuale omogeneo. Forse potremmo dire che il fatto che l'universo sia omogeneo IMPLICA un Big Bang, ma potrebbe esserci stato anche senza un universo omogeneo. Il che ci fa cadere nell'asimmetria tra materia e antimateria e il gioco si fa veramente duro per tutti e dico proprio tutti!
Insomma, siamo ancora in mare molto aperto (mare di Dirac, ovviamente... :mrgreen:)
Bravo come sempre caro Paolo: il caldo non ti ha "sciupato" la logica...
caro Gaetano,
dici bene, ovviamente! Si parla solo di eventi che possono essere descritti da funzioni d'onda.
Se in un dato riferimento (O,T) l'evento A è "genero un neutrone",l'evento B "rilevo il decadimento del neutrone " in un altro ,possibile ,riferimento l'evento B può precedere l'evento A ?