Eccoci alla soluzione del quiz sull’unità di tempo (QUI). In realtà, i nostri bravissimi esperti relativistici hanno già dato la risposta con grande classe e sicurezza. Tuttavia, penso che non sia male approfittare di questo “gioco” puramente geometrico per ripetere ancora una volta, in modo un po’ diverso, il funzionamento dell’orologio a luce e come esso porti in modo elementare al fattore di Lorentz, attraverso un semplice triangolo rettangolo e l’applicazione del teorema di Pitagora.

In pratica, utilizziamo un piccolo dramma spaziale, che si risolve velocemente tenendo conto che la velocità della luce rimane costante in qualsiasi sistema di riferimento.

Preambolo

Prima di raccontarlo, invito tutti a non confondere le figure che troveremo con il diagramma di Minkowski. In altre parole, la nostra astronave e i percorsi della luce sono raffigurati nello spazio di chi sta fermo e non vi è nessun asse del tempo. Passando, invece a Minkowski, si ha una rappresentazione spaziotemporale (anche se con una sola dimensione spaziale). Certe grandezze rimangono inalterate, ma bisogna saperle … comprendere bene.

In parole povere, vogliamo dimostrare che un banale triangolo rettangolo e l’applicazione del teorema di Pitagora, ci permette di ricavare un fattore fondamentale per la teoria della relatività: il fattore di Lorentz, quello che controlla la dilatazione del tempo e molte altre cose.  Il valore di questo fattore gamma compare nel triangolo, così come lo spazio percorso dall’astronave che viaggia a velocità v. La conoscenza di due lati del triangolo ci permette di applicare il teorema di Pitagora allo stesso triangolo che ritroviamo nel diagramma di Minkowski, sempre riferito al sistema fermo, e di calcolare immediatamente il segmento unitario sull’asse del tempo.

Questa avventura (già presentata nel vecchio sito)  sta a metà tra un racconto papalliano e le più “seriose” lezioni che abbiamo trovato nella descrizione completa della Relatività Ristretta o Speciale. E’ quindi adatto veramente a tutti, così come la soluzione finale.

Innanzitutto, chiariamo subito che la teoria della relatività nasce decisamente con Galileo Galilei e la si trova espressa perfettamente nel suo celebre scritto: Dialogo sopra i due massimi sistemi del mondo (andate a leggerlo… è veramente fantastico!). Essa può sintetizzarsi in un principio facilmente comprensibile: le leggi della meccanica devono valere per tutti i sistemi di riferimento inerziali. Chi conosce un po’ di meccanica, sa benissimo cosa vuol dire sistema inerziale. Tuttavia, l’enunciato di prima si può semplificare ancora di più dicendo che leggi della meccanica rimangono inalterate qualunque sia la velocità del corpo o del sistema che si sta studiando. L’importante è che la velocità sia costante.

Ricordiamo, inoltre, che Galileo aveva già intuito che la sua relatività era solo un’approssimazione di qualcosa di ben più generale. Aveva capito perfettamente (attraverso vari esperimenti) che la luce viaggiava a una velocità che non doveva essere infinita. Tuttavia, aveva concluso che era talmente alta da non influire sulle leggi della Natura e aveva accantonato il problema (nel XVII secolo era più che ammissibile). Era quindi ovvio che per lui il tempo fosse sempre lo stesso, in qualsiasi sistema di riferimento. Un’azione che si compiva in tre secondi su un sistema, avrebbe impiegato lo stesso tempo anche su un sistema in movimento rettilineo uniforme rispetto al primo.

La vera novità di Einstein è stata, quindi, quella di affrontare il problema della velocità della luce, c, e di asserire non solo che era finita (circa 300 000 km/sec), come risultava da vari esperimenti, ma che essa rimaneva costante in qualsiasi sistema inerziale. In altre parole essa era indipendente dalla velocità con cui si muoveva la sorgente che aveva generato la luce.

Una conclusione, che sembrerebbe inoffensiva, è stata invece rivoluzionaria. Basti pensare che la velocità è uno spazio diviso per un tempo. Se la velocità della luce non può cambiare, vuol dire che se varia lo spazio è costretto a variare anche il tempo e viceversa. La costanza della velocità della luce ha stravolto il concetto di relatività galileiana. Passando da un sistema inerziale a un altro, le grandezze non si conservano più. Relatività vuol proprio dire che le misure dello spazio e del tempo sono relative al sistema di riferimento utilizzato.

Una strana astronave

Abbiamo solo bisogno di un’astronave (un po’ strana per la verità), di un coraggioso astronauta A e di un punto di osservazione nello spazio (magari un asteroide o meglio ancora un satellite di Saturno) dove recarci per vederla passare quando ormai ha raggiunto una velocità di crociera v, molto elevata ma costante. Utilizziamo, perciò, un sistema di riferimento considerato fermo.

L’appuntamento con l’astronave è già fissato e il nostro astronauta accenderà una luce per farsi vedere e dimostrare che tutto va bene. E’ l’unico sistema, perché la radio raffinatissima di bordo potrà essere accesa solo quando uscirà dal Sistema Solare (fuori dal campo magnetico solare) e ci vorranno parecchi mesi. Non può consumare energia, per cui deve lasciare la luce accesa solo per un tempo brevissimo: giusto quello necessario alla luce inviata dalla lampada L per raggiungere la sua testa.

Sia T questo tempo, che l’astronauta ha misurato più e più volte prima della partenza, sotto gli occhi attenti di noi che lo stiamo aspettando.

Superare T vorrebbe dire rischiare di restare senza energia nel caso di problemi inattesi. La Fig. 1 ci mostra la strana astronave con il suo motore a bosoni alternati. La cabina di comando è completamente trasparente, in modo che sia visibile dall’esterno.

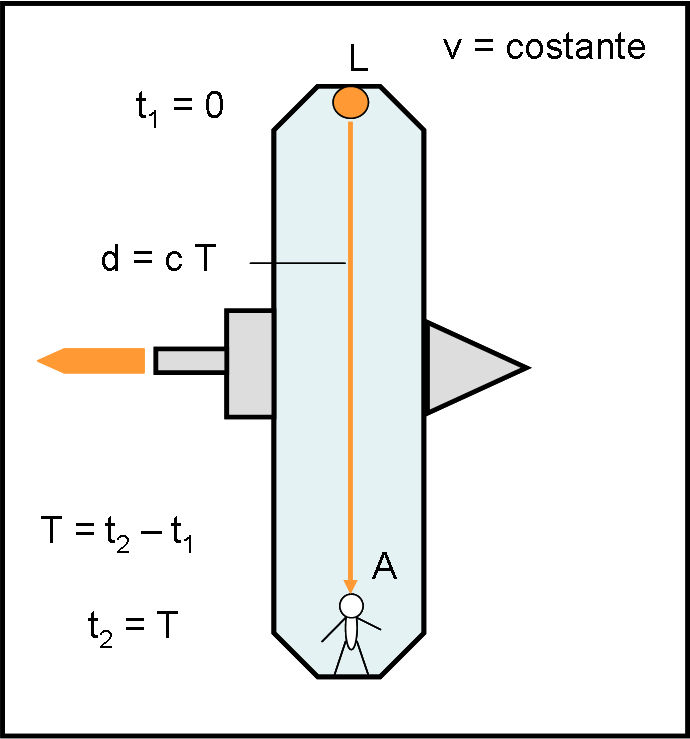
Tutto è pronto per l’incontro. L’astronave è puntualissima e passa proprio davanti alla nostra posizione di vedetta. All’istante t₁ = 0 l’astronauta accende la luce della lampada L che lo raggiunge al tempo t₂. La spegne subito e controlla. Tutto bene: il tempo tra accensione e ricezione è proprio uguale a T. Non ha sprecato energia.

Che distanza ha percorso la luce per raggiungere l’astronauta? Facilissimo: l’altezza della cabina d. Qual è la velocità della luce? Ancora più facile: è la distanza percorsa divisa per il tempo impiegato a percorrerla. Ossia:

c = d/T

da cui si può scrivere senza alcun problema che:

d = c T.

Sono cose che l’astronauta sa già, in quanto ha provato e riprovato la manovra prima di partire e sa benissimo che quello che capita in un sistema di riferimento deve capitare in qualsiasi sistema di riferimento che si muova rispetto ad esso a velocità costante. Proprio quello che sta facendo lui adesso. Per l’esploratore spaziale l’astronave non si muove assolutamente, così come capita per un uomo che sulla Terra si sente immobile anche se il pianeta gira intorno al proprio asse, rivolve attorno al Sole e insieme a lui attorno al centro della galassia, a velocità non certo trascurabili. Basta ricordare il primo enunciato di Galileo che è stato ripreso e rafforzato da Einstein: “Le leggi della fisica devono valere per tutti i sistemi di riferimento inerziali”.

Tutto bene allora? Sembrerebbe di sì. Perché allora l’astronauta vede un gesto di disperazione da parte nostra che lo guardiamo dal satellite di Saturno? Lui non capisce, eppure abbiamo proprio ragione a essere spaventati e preoccupati. Noi abbiamo misurato il tempo T’ tra accensione della luce e l’arrivo sulla testa dell’astronauta  e purtroppo è risultato più lungo di quello accettabile T.

Accidenti! L’astronauta ha tenuto la luce accesa troppo a lungo. Addio energia…

Passiamo pochi minuti di scoraggiamento e poi ci riprendiamo. Che sciocchi siamo stati. Abbiamo preso per buoni i principi di Einstein, ma non abbiamo pensato a quello che avrebbero causato. E pensare che basta conoscere il teorema di Pitagora!

Il nostro T’ non è quello misurato dall’astronauta! E’, effettivamente, più grande del giusto, ma non perché la luce è stata tenuta accesa troppo a lungo. E’ maggiore solo perché lo abbiamo misurato in un sistema di riferimento diverso. L’importante è che sia giusto il T misurato dall’astronauta che si muove con l’astronave. Quello è veramente perfetto e il pericolo scongiurato.

Vediamo, allora, in Fig. 2 come sono andate realmente le cose.

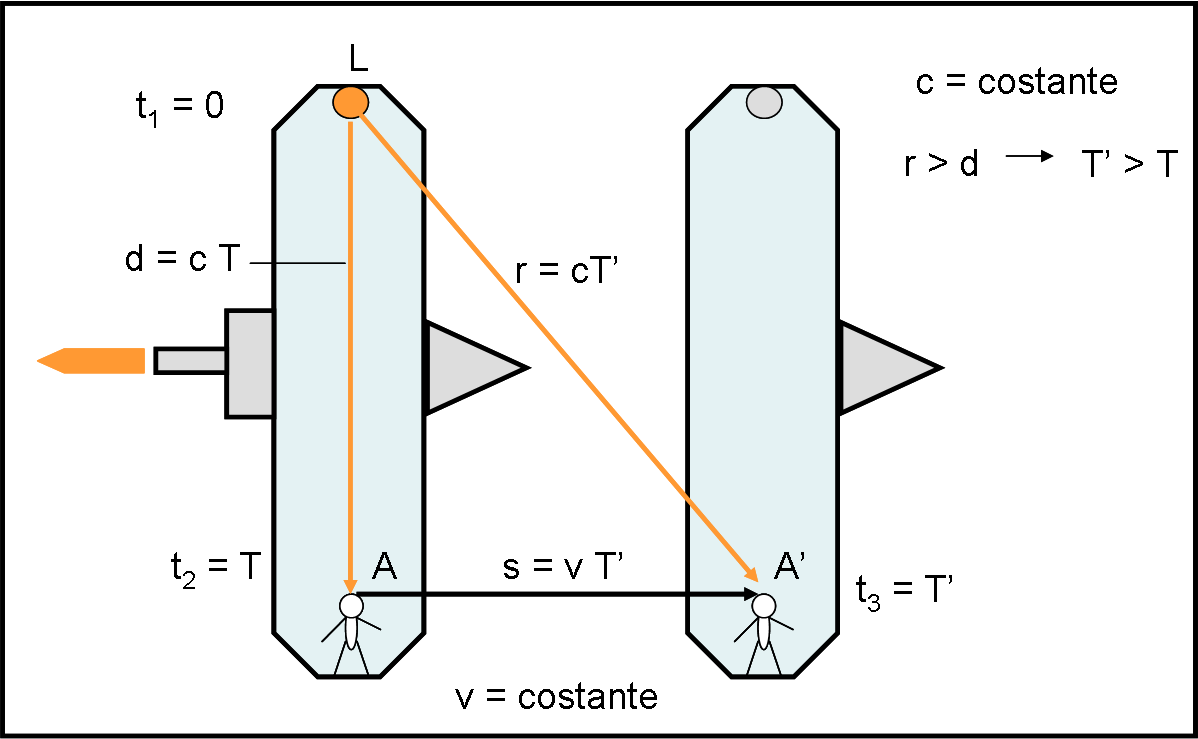
All’istante t₁ = 0 si accende la lampadina. Mentre la luce viaggia verso l’astronauta, quest’ultimo, insieme alla sua astronave, si muove con velocità v che noi percepiamo benissimo. Se dessimo ragione alla meccanica classica di Newton, per sapere lo spazio percorso dalla luce per arrivare sulla testa dell’astronauta, dovremmo sommare la velocità della luce a quella dell’astronave. Insomma, un banale esercizio di cinematica.

Tuttavia sappiamo benissimo (ce lo ha detto Einstein) che la velocità della luce è la massima possibile e ad essa non si può sommare un bel niente! Ossia:

v + c = c, qualsiasi sia v.

Passiamo allora al triangolo rettangolo LAA’, che descrive perfettamente ciò che vediamo noi dal satellite. La distanza d tra luce e astronauta è quella che è (la conosciamo benissimo avendola misurata a Terra). L’astronave, prima che la luce tocchi la testa dell’astronauta, si è mossa di uno spazio s per effetto della sua velocità v. Lo possiamo misurare senza difficoltà.

La luce deve allora aver percorso il tragitto LA’ = r per raggiungere il pilota. Quanto vale il percorso r della luce, nel nostro sistema di riferimento (nel quale vediamo muoversi l’astronave a velocità v)? Presto detto è:

r = T’ c … (1)

Ovviamente, la velocità della luce è sempre la stessa e non è superabile: al posto di un’ipotetica somma vettoriale di v e di c, abbiamo inserito c, come ci dice Einstein.

E’ ovvio, quindi, che, dato che r > d, sia anche T’ > T: il tempo trascorso dall’accensione della lampadina a quando la luce tocca la testa dell’astronauta è diverso se osservato dal satellite rispetto a quello osservato dall’astronauta.

Galileo aveva torto. Cambiando sistema inerziale il tempo non si conserva. L’errore che abbiamo fatto è stato proprio quello di avere creduto a Galileo e aver pensato che T’ misurato da noi dovesse essere uguale a T misurato dall’astronauta.

Per convincerci definitivamente, è meglio quantificare la differenza tra i due tempi. Ci basta applicare il teorema di Pitagora al triangolo LAA’, di cui conosciamo tutto.

r² = d² + s² … (2)

ossia:

c²T’² = c²T² + v²T’²

sviluppando e giocando un po’ con i numeri:

T’² = T² c² /(c² – v²) = T²/((c² –v²)/c²) = T²/( 1 – v²/c²)

e, infine, (estraendo la radice quadrata):

T’ = T/(1 – v²/c²)^½   … (3)

Come previsto, il tempo misurato da noi (T’) non è assolutamente uguale a quello dell’astronauta, ma decisamente più lungo.

Dato che v/c < 1 (per definizione) ne segue che anche  (1- v²/c²)^½ < 1. Dividere T per un numero minore di 1 vuol dire ottenere un numero T’ più grande. Ecco perché ci eravamo spaventati!

Usando la (3) al contrario (ossia ricavando T dal T’ misurato da noi) troviamo che il tempo in cui è stata accesa la luce nella cabina è proprio quello giusto per non sprecare energia preziosa.

La quantità  γ = 1/(1 – v²/c²)^½  è il celebre fattore di Lorentz, ossia il fattore che ci permette di calcolare quanto il tempo si è "apparentemente" dilatato passando da un sistema di riferimento inerziale a un altro.

Non è certo stato difficile. Eppure, attraverso un semplice triangolo rettangolo, abbiamo in mano uno strumento fantastico per entrare nei misteri della relatività ristretta: orologi impazziti, elisir dell’eterna giovinezza e buchi neri impenetrabili.

Da ciò che abbiamo sperimentato, risulta chiaro che la costanza della velocità della luce comporta una dilatazione del tempo. In poche parole, il nostro orologio gira più in fretta. Tanto per fare un esempio: tre secondi per l’uomo dello spazio possono equivalere a cinque secondi per noi. O, andando oltre, 30 anni per lui sono ben 50 anni per noi. Insomma, andando sull’astronave si invecchia di meno… Al limite, se l’astronauta andasse alla velocità della luce, la (3) diventerebbe:

T’ = T/(1 – 1) = 1/0 = infinito.

Per noi, l’astronauta impiegherebbe un tempo infinito per compiere il più piccolo tragitto possibile, ossia lo vedremmo fermo. Noi invecchieremmo e per lui non sarebbe passato nemmeno una frazione di secondo. Il suo orologio non girerebbe.

Conclusasi al meglio quest'avventura spaziale, disegniamo di nuovo, schematicamente, il triangolo rettangolo LAA’ (Fig. 3), ponendo, come detto la volta scorsa, c = 1, e 1 anche il tempo unitario necessario alla luce per partire dalla lampada e arrivare sulla testa dell’astronauta (quello che abbiamo chiamato T). I lati del triangolo rettangolo diventano perciò 1, γ e γv, dove γ è l’ipotenusa.

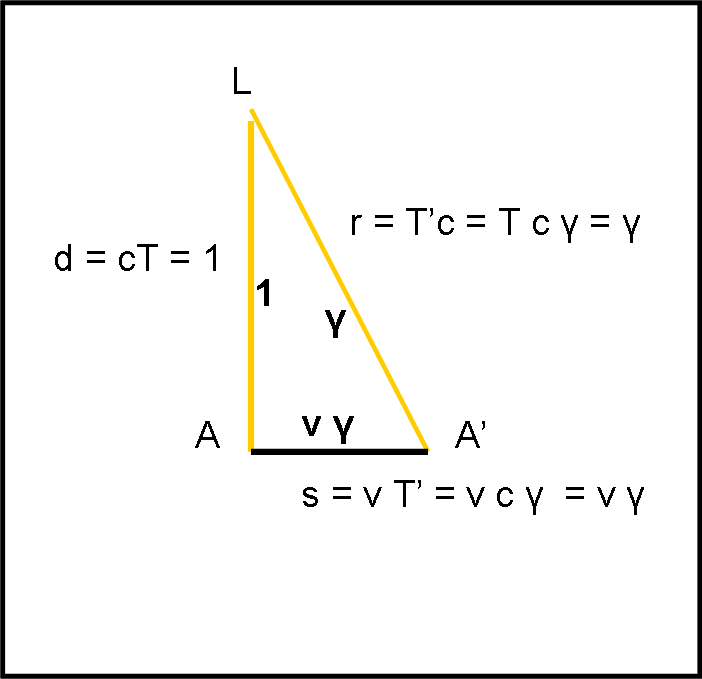
L’ipotenusa, ossia γ,  è il tragitto della luce vista dall’osservatore fermo, ma è anche il tempo percorso (c = 1). γ v è lo spazio percorso  dall’astronave, nel sistema fermo. Possiamo quindi passare alla figura proposta nel quiz, che adesso chiamiamo Fig. 4. Tracciamo la perpendicolare dal punto unitario del tempo dell’astronauta (il dato di partenza). Visto dal sistema rosso, questo segmento non è altro che il tempo osservato γ, mentre il segmento orizzontale tra l’origine e il piede di questa perpendicolare non è altro che lo spazio percorso, misurato nel sistema rosso, dall’astronave che viaggia a velocità v.

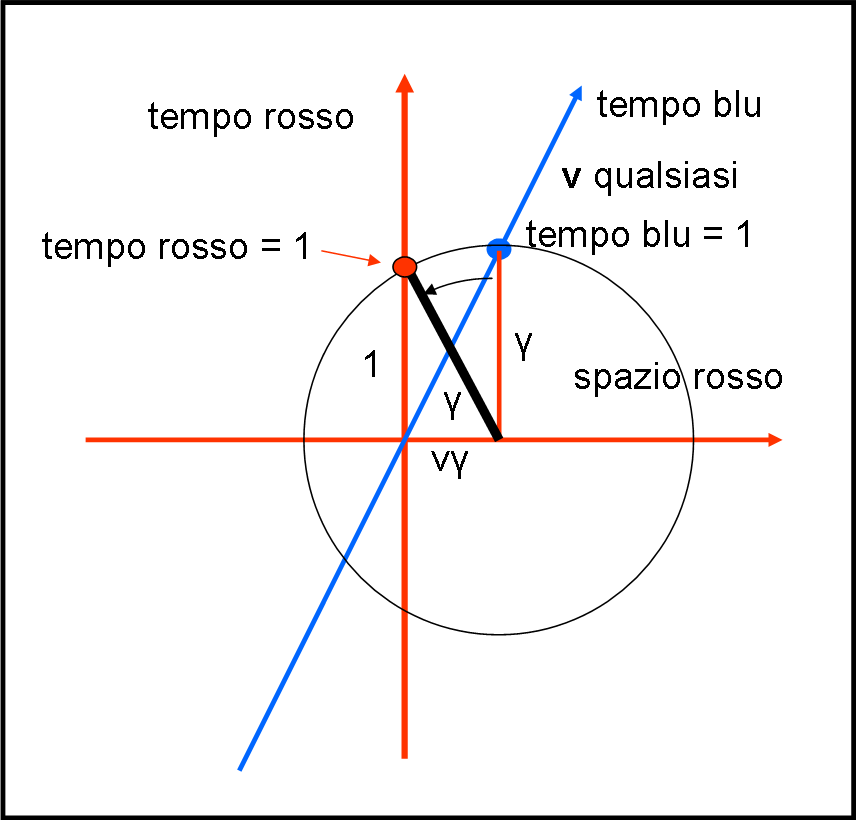
Non ci resta che fare centro nel piede della perpendicolare e tracciare il cerchio di raggio γ fino a intersecare l’asse del tempo rosso. Otteniamo esattamente il triangolo rettangolo di Fig. 3, ossia quello ottenuto con l’orologio a luce. Il cateto maggiore deve, allora, essere proprio l’unità di tempo rosso.

E' o non è semplice la costruzione geometrica (una volta capita la relazione tra orologio a luce e diagramma di Minkowski)? Come fatto notare dai nostri solutori, la faccenda vale per qualsiasi velocità v e quindi tutti i cerchi che si costruiscono devono passare per il punto unitario del tempo rosso. D’altra parte cambiando la velocità, cambia il fattore gamma e quindi cambia il raggio, ma ci si riferisce sempre al tempo unitario del sistema rosso.

Ancora “BRAVI” ai solutori e spero che con questa lunga spiegazione, il problema sia ora chiaro a moltissimi altri.

Per una trattazione completa della Relatività Ristretta, si consiglia di leggere il relativo approfondimento