Categorie: Fisica classica
Tags: energia cinetica gravità quiz urto anelastico
Scritto da: Vincenzo Zappalà
Commenti:33
QUIZ: un canguro papalliano ***/**
Il Quiz può essere diviso in due parti. La prima un po’ più complicata, la seconda decisamente più facile. Chi non se la sente, può partire direttamente dal risultato della prima e proseguire con l’esercizio papalliano.
In realtà, infatti, descriviamo un altro tipico gioco papalliano che in qualche modo può assomigliare a quello dell’elettrone che va avanti e indietro tra due papalli che viaggiano uno verso l’altro (QUI). In questo caso, però, l’esercizio viene svolto da un singolo papallo in una zona particolare del loro pianeta, l’unica in cui esiste l’attrito e che, soprattutto, non permette di rimbalzare in modo perfetto sul terreno.
In poche parole, un papallo che si lanci da un trampolino verso il basso rimbalzerà sicuramente sul terreno, ma non riuscirà a tornare alla stessa altezza di prima e la cosa si ripete quando tocca nuovamente il terreno. Insomma, i rimbalzi sono sempre meno alti e prima o poi è costretto a fermarsi. In modo “professionale” possiamo dire che l’urto del papallo sul terreno è anelastico, ossia una certa parte di energia cinetica viene trasformata in un altro tipo di energia (calore, ad esempio, ma a noi poco importa), per cui nella risalita non può raggiungere la stessa altezza della partenza… e via dicendo: ogni rimbalzo è sempre meno alto di quello precedente…
Prima parte
Definiamo il coefficiente di restituzione e tramite la seguente formula:
ECD = ECP e2 …. (1)
A parole, possiamo dire che l’energia cinetica dopo l’urto è uguale a quella prima dell’urto moltiplicata per il quadrato del coefficiente di restituzione.
Il coefficiente può variare, ovviamente, tra 0 e 1. Se e = 0, l’urto è completamente anelastico (non vi è nemmeno un rimbalzo), mentre, se e = 1, l’urto diventa completamente elastico e i rimbalzi proseguono sempre allo stesso modo: l’energia cinetica dopo l’urto è uguale all’energia cinetica prima dell’urto e il papallo continuea ad andare su e giù senza mai fermarsi.
La prima parte del quiz (A) chiede di dimostrare che se vale la (1), allora deve valere anche:
vD = - e vP
dove vD è la velocità del papallo dopo l’urto, mentre vP è quella prima dell’urto.
Seconda parte
Dimostrato o accettato questo risultato, iniziamo con il gioco papalliano.
Papalatleta si lancia da una certa altezza h con velocità iniziale uguale a zero e cade sotto l’effetto della sola accelerazione di gravità che su Papalla è uguale a quella terrestre (g). Come detto, il rimbalzo lo porta a un'altezza minore e via dicendo fino a che si ferma completamente.
Il papallo ha massa mP.
Una prima domanda (B), che vuole una risposta solo istintiva, è la seguente: a parità di altezza e di coefficiente di restituzione, vince (ossia si ferma più tardi) sempre il papallo più pesante o quello più leggero?
La seconda (C1) è: quanto tempo impiega il papallo per fermarsi al suolo?
Per chi vuole andare un po’ oltre, possiamo anche chiedere:
(C2): Che distanza percorre il papallo prima di fermarsi?
Sarà anche interessante (in un secondo tempo) fare dei casi numerici e sfruttare le capacità grafiche dei papallicoli!
P.S.: ho tolto l'ultima domanda per non appesantire troppo il quiz...
QUI trovate la prima parte della soluzione
QUI trovate la seconda parte della soluzione






33 commenti
Ciao in merito alle ultime domande cosa intendi per "fermarsi al suolo" (e non aggiungo altro...)
fermarsi, Mik... non rimbalzare più...
Ciao,
la resistenza del mezzo (durante la caduta e la risalita) è considerata trascurabile ?
Sì, Arturo... su Papalla non c'è atmosfera. Solo un coefficiente di restituzione minore di uno (ma non uguale a zero).
Non finirò mai di stupirmi della tua fantasia; veramente stimolante! aspetto..
Bravo Umberto, aspetta ancora un po'... io credo (spero!) di avere compreso il meccanismo fisico, ma ora si impone lo studio di alcune lezioni di matematica che, ahimè, avevo saltato
E' si Daniela.. c'è molta matematica dietro a questo quiz..
Come sempre, del resto... e, tanto per cambiare, il nostro Enzo si diverte anche a tendere qualche trabocchetto... chissà come se la sta ridendo in questo momento!
ma no, cosa dici mai Dany... nessun trabocchetto ( ) e la matematica non è poi molta (ricordiamoci l'elettrone vagante...
) e la matematica non è poi molta (ricordiamoci l'elettrone vagante...  ).
).
Grazie ragazzi per la vostra attesa....
L'elettrone me lo ricordo, ma qui secondo me c'è una differenza importante rispetto a quel caso e mi sembra che salti all'occhio solo guardando le formule, ancora prima di svolgere i calcoli (sempre che abbia impostato bene le formule)... va beh, vedremo, intanto vado a studiare un po' di matematica che non fa mai male!
Dunque, mi sto chiedendo : ma davvero la seconda parte era quella decisamente più facile ?... ;-)
E' la stessa domanda che mi sono fatta io dopo aver risolto la prima parte più velocemente di quanto pensassi...
cari amici,
come dice la teoria della relatività, anche la facilità è... relativa

Quindi, vista da alcuni sistemi di riferimento la prima domanda appare più difficile, vista da altri è la seconda parte a risultare più difficile...
 io penso di stare in quello che vede più semplice la prima domanda..
io penso di stare in quello che vede più semplice la prima domanda..
Per la seconda io ho trovato utile affiancare all'approccio matematico anche uno grafico, con un diagramma che inquadra il problema... ma ognuno ha il suo approccio ... e non è detto che la soluzione che ho travato sia quella giusta...
... e non è detto che la soluzione che ho travato sia quella giusta...
Ovviamente per ora non posto nulla.. semmai rinnovo l'invito ai meno noti di provare a rispondere partendo dalle domande a cui si pensa di saper rispondere... magari si può partire dalla B...
Paolo
NOTA BENE:
mi sono accorto, dai primi commenti, che la prima parte potrebbe essere affrontata troppo semplicemente. In prima approssimazione potremmo anche accettare questa semplificazione (mi interessa di più la seconda parte...). Per chi vuole, però, una trattazione più completa e fisicamente corretta, aggiungo qualche parola in più e un avvertimento.
Si definisce urto anelastico un urto in cui si conservi la quantità di moto, ma non l'energia cinetica e, inoltre, in cui le due masse coinvolte non proseguano come un unico corpo (se no cadremmo nell'urto completamente anelastico). Attenzione, però: il suolo di Papalla non può essere considerato perfettamente fermo, dato che se lo immaginassimo immobile, sarebbe come se gli applicassimo un vincolo esterno. Un vincolo esterno è una forza esterna che agirebbe sul sistema papallo + Papalla e, di conseguenza, non si conserverebbe la quantità di moto. Alla fine dei calcoli, può poi essere fatta l'approssimazione che c'interessa...
Consiglio vivamente (Paolo ha detto qualcosa a riguardo, ma non so se riferita al nostro problema) di usare come sistema di riferimento per lo studio dell'urto, un sistema particolare, capace di semplificare di molto i passaggi...
Non dico ancora quale sistema, per adesso...
Non obbligo nessuno e, come sempre, può darsi benissimo che qualcuno abbia usato un approccio diverso, altrettanto valido di quello che ho in mente io
Figuriamoci se non c'era una "trappola" perdonami Enzo, ma credo proprio che lascerò la prima parte come l'avevo ipotizzata (troppo semplice per essere vera!), sperando di avere fatto qualcosa di giusto nella seconda...
perdonami Enzo, ma credo proprio che lascerò la prima parte come l'avevo ipotizzata (troppo semplice per essere vera!), sperando di avere fatto qualcosa di giusto nella seconda... 
Non so se ho inteso correttamente.... gulp, io nella soluzione, che ho terminato, ho usato un altro approccio...
Su alcune cose che hai detto devo rifletterci meglio... torno al silenzio da quiz....
Paolo
caro Paolo,
non farti suggestionare... come capita sempre in fisica, ci sono sempre vari modi per arrivare alla meta e può darsi benissimo che il mio approccio non sia il migliore o il più rapido... Tieni solo conto della definizione di urto anelastico e nulla più... conservazione del momento, ma non dell'energia cinetica e masse che si urtano separate dopo l'urto.
Ho scelto questo tipo di approccio per parlare un po' di cambiamento di sistemi in casi di urti particolari... niente di più...
cari TUTTI,
forse avete capito che la prima parte è meno semplice del previsto (almeno usando una trattazione accurata fino in fondo). Non bloccatevi, però... la seconda parte è decisamente alla portata di MOLTI, soprattutto ricordando il quiz sull'urto papalliano... Partite pure da vD = - e vP
Più che altro mi incuriosiva il problema della quantità di moto che si deve conservare, per cui ho inserito un'appendice alla soluzione su questo... poi si vedrà....
Paolo
La quantità di moto si conserva sempre... se non ci sono forze esterne.
Magari trattiamo a parte tutti i tipi di urto... che ne dici?
Hai ragione Enzo, solo che non mi ero preoccupato di controllare se si conservava e come.... un errore di dimenticanza...
Paolo
Bene, provo a rispondere alla prima parte e alla domanda B della seconda. Il resto a seguire.
Prima parte
Il sistema di riferimento da me assunto , che consente di evitare complicazioni di calcolo, è quello del centro di massa del sistema costituito dal papallo (massa mp) e dal pianeta Papalla (massa M). Poiché M>>mp, tale sistema di riferimento coincide praticamente con il sistema inerziale rispetto al pianeta Papalla. In tale sistema di riferimento (del centro di massa), la quantità di moto totale si mantiene costantemente nulla, mentre per l’energia cinetica vale la relazione (la variazione di energia cinetica tra dopo e prima del primo rimbalzo deve essere pari a quella derivante dall’ipotesi posta nel testo del problema):
per l'ipotesi risulta:
(1)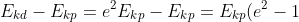=\frac{1}{2}m_{p}v_{p}^{2}(e^{2}-1))
nel sistema di riferimento considerato risulta
(2)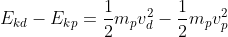
confrontando la (1) e la (2) si ottiene:
moltiplicando primo e secondo membro per 2 e dividendo per , portando a primo membro il termine
, portando a primo membro il termine 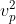 e svolgendo i calcoli alla fine si ottiene:
e svolgendo i calcoli alla fine si ottiene:
cioè:
Poiché il papallo , al rimbalzo, inverte la direzione del moto, non puo’ che essere, quindi:
Seconda parte (domanda B)
La massa del papallo è ininfluente in questo problema, perché si è ritenuta trascurabile la resistenza del mezzo. Infatti, come si è visto nella risposta alla prima parte del quiz, in tale ipotesi il termine si semplifica nei passaggi matematici, quindi è come se non ci fosse.
si semplifica nei passaggi matematici, quindi è come se non ci fosse.
La massa (insieme alla forma) del papallo entrerebbero in gioco nel caso in cui non si trascurasse la resistenza del mezzo.
Quelle che seguono sono le mie risposte alle domande C1 e C2 della seconda parte del quiz. Le vedete come immagini perché le ho scritte ieri con Word e salvate come immagine su un server, e non mi andava di riscrivere le formule con l'editor del blog Chiedo venia.
Chiedo venia.
Seconda parte (domanda C1)
Seconda parte (domanda C2)
caro Arturo,
non dico niente sulla seconda parte, lasciando ancora spazio a TUTTI gli altri...
Commento solo la prima parte.
Tu dici che la quantità di moto totale risulta costantemente nulla, sia prima che dopo l'urto, se ho capito bene...
Ma in questo caso avresti mvp = 0, ossia vp = 0, dato che è l'unico fattore della quantità di moto totale prima dell'urto. Attenzione! Se consideri immobile il suolo, gli imponi un vincolo e non hai più la conservazione della qm!
Se invece considerassi, in un sistema inerziale, la conservazione della qm avresti:
mvp + 0 = mvd + 0
Ossia
vp = vd
entrambe le cose non possono essere vere.
Inoltre, ciò che tu hai fatto non è altro che scrivere le ipotesi di partenza:
ECD = ECP e2
mvd^2 = e^2 mvp^2
ossia:
vd= +/- e vp
Come ho detto nei commenti, questa soluzione può anche accontentarci in prima approssimazione, ma non bisogna pretendere che sia una soluzione corretta completamente. Penso sia quella prospettata anche da Dany e -forse- Paolo...
Provo a giustificare la prima parte con un ragionamento che potrà sembrare un pò strampalato.
Considero l'urto fra due masse m e M (VM prima dell'urto è 0)
energia cinetica prima e dopo l'urto:
quantità di moto prima e dopo l'urto:
ricavo VM:
sostituisco nella formula dell'energia:
Considero il suolo come una massa infinita.
se faccio il limite per M tendente a infinito del secondo membro ottengo:
quindi non dipendendo il primo membro da M:
(prendiamo il segno meno perchè la velocità dopo il rimbalzo si inverte in direzione). La prima velocità è quella che si ottiene dalla caduta con accelerazione g: la troviamo eguagliando l'energia potenziale con l'energia cinetica:
ma consideriamo solo il modulo della velocità e applichiamo la 1) :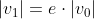 ; applichiamo ancora la 1) per il secondo rimbalzo e otteniamo
; applichiamo ancora la 1) per il secondo rimbalzo e otteniamo 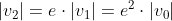 e così via. Otteniamo per il generico rimbalzo n:
e così via. Otteniamo per il generico rimbalzo n:
La velocità in funzione dei rimbalzi appartiene ad una curva esponenziale, che tende a zero per n tendente a infinito,essendo e<1.
Calcoliamo adesso gli intervalli di tempo dall'inizio in funzione di n. Sappiamo che il primo intervallo si calcola così:
.
.
per calcolare il tempo finale, bisogna sommare tutti questi intervalli di tempo, che sono infiniti.
ricordando che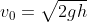 , la formula finale in funzione solo di h e g diventa:
, la formula finale in funzione solo di h e g diventa:
Per calcolare lo spazio percorso esprimiamo l'altezza dei rimbalzi in funzione della velocità:
da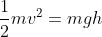 otteniamo
otteniamo 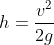 ; se ho è la prima altezza,
; se ho è la prima altezza, 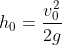 , per calcolare h1 dobbiamo usare v1:
, per calcolare h1 dobbiamo usare v1:
il termine generale sarà dunque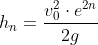 ;
;
adesso dobbiamo sommare tutti gli spazi percorsi ho,h1,h2,...hn
é ancora la somma di una serie:
ricordando che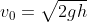 ,
,
Entrambi i risultati non dipendono dalla massa.
Buon giorno Vincenzo e tutti,
nella mia risposta al quesito A ho considerato come sistema di riferimento quello del centro di massa tra mp e M. In generale, se M non è >> mp, avrei, pure per M, una velocità diversa da zero anche prima dell'urto , se riferita appunto al centro di massa. Ma la quantità di moto complessiva, sempre rispetto al centro di massa, resterebbe pari a zero. Nel caso specifico, si ha invece che M>>mp, per cui, il sistema del centro di massa va a coincidere praticamente con quello inerziale rispetto ad M. Non è che io consideri fermo M dopo l'urto, ma in pratica è come se lo fosse. In una trattazione rigorosa, avrei in effetti una Vd anche per M (con relative quantità di moto ed energia cinetica), ma Vd sarebbe talmente irrisoria da poterla trascurare.
Chiaro poi che io non pretendo affatto che la soluzione da me esposta sia quella completamente corretta. Ho iniziato a scriverla dicendo "provo a rispondere". Cioè, vediamo se è quella giusta , anche se in prima approssimazione
Caro Enzo per trovare la soluzione ho deciso di usare tre semplici figure.
La prima figura descrive solo il salto di PapalAtleta, usando un diagramma che rappresenta l'altezza dal suolo ed il tempo trascorso.
Innanzitutto la figura risponde parzialmente alla domanda A (su questa ci torno alla fine): basta sostituire a Ecp = ½ mp Vp² ed a Ecd= -½ mp Vd², e la massa di PapalAtleta, o meglio la sua metà (½ mp) scompare dall'equazione e con un semplice passaggio matematico si ottiene che Vd=-Vp e.
La massa di PapalAtleta è ininfluente sulla velocità acquisita....
D'altronde su PapalAtleta agisce solo la Forza di Gravità e tale forza è uguale a: F = GMmp/r²..... F= ma, e l'accelerazione è quella di gravità, ossia g, quindi: g= F/mp....... F/mp = GMmp/mp r² = GM/r²
g=GM/r²
L'accelerazione che subisce il corpo è indipendente dalla sua massa... forse sarà anche per questo che Einstein ha pensato alla gravità come una deformazione della struttura geometrica dello spaziotempo dovuta alla presenza di grosse masse...
Quindi la risposta alla domanda B dovrebbe essere: non vince nessuno poiché la massa di PapalAtleta è ininfluente sulla sua accelerazione.
L'Energia di potenziale è stata indicata in funzione del suolo, ossia come gmh. In forma sintetica ho provato a ricavare tale formuletta..
Rispetto al suolo, prima del salto l'Energia Totale era solo quella di potenziale, ossia mgh, quando PapalAtleta raggiunge il suolo l'Energia totale (rispetto al suolo) è solo quella cinetica ½mVp² (rispetto al suolo h=0, per cui Epot=mgho = mg(0)= 0).
Dato che l'Energia totale deve conservarsi mgh=½mVp², da cui si ricava: Vp=√2gh.
Infine nell'intervallo di tempo (t1-t0), PapalAtleta, partendo da fermo, raggiunge il suolo, ossia percorre lo spazio pari all'altezza h accelerato dalla gravità g, quindi:
S= h = ½ mgt1², da cui si ricava che: t1 = √2h/g.
La seconda figura descrive cosa accade urto dopo urto, usando la relazione Vd =-Vpe
Prima del primo urto la Velocità al suolo di PapalAtleta era uguale a Vp=gt1.
PapalAtleta dopo l'urto riparte con una velocità minore in senso opposto: Vd = -Vp e, quindi: Vd = - gt1 e
L'accelerazione di gravità g è una costante per cui ciò che cambia è il tempo che da t1, diventa t1 e......
Con questa velocità PapalAtleta, frenato dall'accelerazione di gravità, raggiunge velocità zero, quando: V= - g(t1 e) + g(t1 e) = 0.
A quel punto PapalAtleta ricade verso il suolo, accelerato dalla forza di gravità e lo raggiunge a velocità: V=g(t1 e).
La stessa cosa si ripete urto dopo urto, ed ogni volta la nuova velocità prima dell'urto viene moltiplicata per e... quindi ad ogni urto e viene moltiplicata per se stessa: e e = e²....... e e e = e³.
Il tempo totale, deve tener conto che tra un urto e l'altro PapalAtleta deve percorrere la stessa distanza salendo e scendendo, per cui impiega il doppio del tempo...
Il tempo Totale è dato da t1 sommato a tutti i tempi intercorsi tra un urto e l'altro:
Giusto per fare una prova se e= :
T(tot) = t1 +2t1(0) +2t1(0)² 2t1(0)³...= t1
se e= 1: T(tot) = t1 +2t1(1) +2t1(1)² +2t1(1)³...= t1 +2t1+2t1+2t1....
Il tempo t1 si può sostituire con t1= √2h/g e si può sintetizzare tutto con una sommatoria (come mostra la figura precedente, dove nella sommatoria n è il numero degli urti) così compare solo l'altezza e l'accelerazione di gravità il cui valore vicino al suolo è costante...
Non resta che concludere il ragionamento con un'ultima figura:
L'altezza di PapalAtleta, si riduce urto dopo urto... per cui dopo ogni urto sostituisco il nuovo valore del tempo... t1e; t1e²; t1e³..ecc, e con pochi passaggi matematici si ottiene: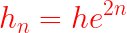
E' ormai evidente che nel quiz i due parametri fondamentali (con g costante) sono h ed e (nella figura e=0,8; h= 19,644 metri)!
Infine lo Spazio Totale percorso deve tener conto che tra un urto e l'altro PapalAtleta deve percorrere lo stesso spazio salendo e scendendo, per cui il percorso è doppio.
Tenendo conto della relazione trovata prima che lega le altezze al coefficiente di restituzione, lo spazio totale percorso da PapalAtleta è:
Per rispondere alle ultime due domande (C1 e C2), conviene fare una ragionamento.
Con lo scorrere del tempo, PapalAtleta raggiunge altezze sempre minori e tra un urto e l'altro trascorre un intervallo di tempo sempre più breve...
Matematicamente si potrebbe continuare con infiniti urti, poiché per quanto possano essere piccole le misure del tempo e dell'altezza, esiste sempre un tempo più piccolo e un'altezza più piccola...
Fisicamente, però, le cose sono un po' diverse (non si può andare oltre il tempo e la lunghezza di Planck )... e conviene decidere fino a quale grado di approssimazione si vuole arrivare..
Cosa succede quando dopo un certo numero di rimbalzi PapalAtleta ha raggiunto un'altezza pari al raggio di un atomo?
A parte che entrano in campo altre forze, altrimenti PapalAtleta sprofonderebbe nel suolo, in ogni caso tale altezza sarebbe indistinguibile e PapalAtleta risulterebbe “fermo”..
In fin dei conti senza scendere così in basso con le misure, anche un semplice sassolino sul terreno è leggermente più alto del resto del suolo.. ma non è un gran salto...
In ultimo, tornando alla prima domanda ed alla conservazione della quantità di moto
Considerando M la massa del Pianeta e Va la sua velocità (vista da un sistema esterno), m la massa di PapalAtleta e Vp la sua velocità prima dell'urto, la quantità di moto totale è: qp =mVp + MVa
Dopo l'urto, considerando che :Vd = -Vpe
qd =mVd + MV'a = -mVp e + MV'a
mVp + MVa =-mVp e + MV'a
mVp + mVp e + MVa = MV'a
(Vp+ Vpe) m/M + MVa/M = V'a
(Vp+ Vpe) m/M + Va = V'a
ma m/M è un numero piccolissimo, dato che il divario tra la massa M del Pianeta Papalla e quella m di PapalAtleta è tale che il risultato di questo rapporto è prossimo a zero, quindi: Va ≅ V'a
mVp + MV'a=-mVp e + MVa
mVp + mVp e = MVa - MV'a = M (Va -V'a)
se Va≅ V'a........... Va - V'a ≅ 0
mVp + mVp e = 0
mVp = - mVp e
mVp/m = - Vp e
Vp = - Vp e
Sembra che tutto funzioni, sempre che il ragionamento e la soluzione proposta siano corretti...
Paolo
e per chi volesse vedere l'effetto che fa cambiare il valore del coefficiente di restituzione e , a questo link trovate il grafico della legge oraria del papallo rimbalzante , limitato ai primi 4 rimbalzi.
cambiare il valore del coefficiente di restituzione e , a questo link trovate il grafico della legge oraria del papallo rimbalzante , limitato ai primi 4 rimbalzi.
https://www.desmos.com/calculator/nioxe2ffkg
Per ottenerlo, ho ricavato l'espressione della legge oraria del moto del papallo partendo dalle ipotesi poste a base del quiz. Ho chiamato con c, anziché e, il coefficiente di restituzione perché il sistema interpreta la variabile "e" come il numero di Nepero.
Variando il valore di con l'apposito cursore, si vede come si modifica il grafico.
Giusto per curiosità.
RISPOSTA A
Ovviamente avevo pensato alla soluzione troppo semplice:
dove il segno meno è dovuto al cambiamento di verso di v dopo l'urto.
RISPOSTA B
PapalGalileo mi ha suggerito che, in mancanza di atmosfera, la massa è ininfluente: tutti i papalli, magri o grassi che siano, rimbalzano nello stesso modo. Infatti nelle formule che seguono la massa non compare.
RISPOSTE C
Innanzitutto ho cercato di capire quali formule utilizzare e credo di averle trovate nel capitolo 7 della Fisica Addormentata (quello delle mele e delle ciliegie) e ho suddiviso il problema in tre situazioni:
Situazione iniziale: il papallo si lascia cadere da un'altezza h
Rimbalzo: il papallo torna a salire dopo aver toccato il suolo
Discesa dopo il rimbalzo:
Continuando a calcolare V, t, h per ogni successivo rimbalzo e ricaduta, si ha:
Rimbalzo 2: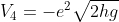
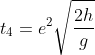
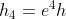
Caduta: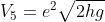
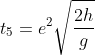
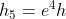
Rimbalzo 3: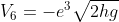
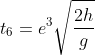
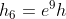
Caduta: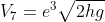
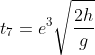
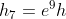
Rimbalzo 4: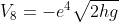
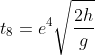
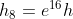
e così via.....
Per rispondere a quanto tempo impiega il papallo per fermarsi e quanta distanza percorre, è necessario trovare qual è l'n-esimo rimbalzo dopo il quale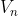 e
e 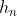 si annullino, ma questo non avverrà mai, infatti:
si annullino, ma questo non avverrà mai, infatti:
Quindi il papallo continuerà a rimbalzare in eterno compiendo salti sempre più piccoli, tendenti a zero... probabilmente, dopo un certo numero di rimbalzi, diventeranno talmente piccoli che il papallo non si accorgerà più di rimbalzare e penserà di essere fermo.
Tuttavia, poiché la somma di infiniti valori infinitesimi, restituisce un valore finito, è possibile calcolare il tempo complessivo dei rimbalzi e la distanza trascorsa, sviluppando queste serie
Ci ho provato, ma sono imbranata, quindi le lascio così e vado a vedere le soluzioni degli altri. Mi accontenterei di non avere commesso gravi errori concettuali...
Daniela, Paolo, Umberto, Arturo... sempre loro... i magnifici quattro!!!
Aspetto ancora un pochino dato che qualcuno (un paio) potrebbero arrivare...
Eh sì, la prima parte era veramente difficile da dimostrare esattamente senza perdere per strada la quantità di moto... Sto scrivendo tutta la trattazione, approfittandone per descrivere l'urto anelastico in modo generale e rifarmi a quanto già fatto ai tempi dell'effetto Compton... (magari cominciate ad andare a vederlo...)
(magari cominciate ad andare a vederlo...) 
Bellissimo l'effetto Compton e spiegato con una semplicità disarmante, me lo vado a rileggere proprio volentieri