Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

Tutto diventa più semplice utilizzando una visione estrinseca. Tuttavia, aver lavorato solo su uno spazio a due dimensioni non euclideo (a parte le figure) ci ha sicuramente fatto entrare meglio nella problematica. Trovate molte ripetizioni, ma non picchiatemi... Certi concetti vanno digeriti molto bene!

Per vedere i risultati ottenuti precedentemente, basta utilizzare una visione dall’esterno, immergendo la superficie sferica in uno spazio a tre dimensioni. Non solo la vediamo, però, ma possiamo manovrare a nostro piacimento altre superfici, come ad esempio i piani. In particolare, siamo in grado di descrivere perfettamente cosa avviene all’interno della superficie sferica, cosa del tutto vietata agli abitanti di sferilandia.

Tagliamo, subito, la sfera con un piano che non passa per il suo centro (lo possiamo fare dato che VEDIAMO il centro della sfera) e otteniamo una circonferenza in cui le due ruote del carrello girano in modo diverso. Bene. Le circonferenze così costruite sono curve sia intrinseche che estrinseche. Ossia esse sono curve sia per chi abita sulla sfera sia per chi vede la sfera da fuori. Chiamiamole cerchi minori.

Prendiamo meglio la mira e utilizziamo un piano che contenga il centro della sfera. E’ immediato comprendere che l’intersezione è ancora una circonferenza, ma questa volta è proprio la linea che abbiamo chiamato geodetica e che non ha curvatura per il carrello che la percorre. Essa è proprio un cerchio massimo. Per chi abita sulla sfera essa non è una circonferenza ma una retta intrinseca (a meno che non sia molto intelligente e si dedichi a un suo studio accurato come abbiamo fatto noi la volta scorsa). L’abitante “medio” della superficie sferica, definisce rette i cerchi massimi, mentre definisce cerchi tutte le intersezioni con piani non passanti per il centro. Per noi che vediamo il tutto da fuori sia i cerchi massimi che quelli minori sono entrambi delle curve. Ne segue che entrambi sono curve estrinseche.

Volendo si può nuovamente dimostrare, ancora più facilmente della volta scorsa, che il cerchio massimo è quello che descrive la minima distanza tra due punti della superficie sferica. Prendiamo due punti qualsiasi e tracciamo la retta (estrinseca) che li congiunge.

A questo punto consideriamo un piano che contiene questa retta. La sua intersezione con la superficie sferica è una circonferenza che deve passare sia per A che per B (per costruzione). Facciamo ruotare il piano attorno alla retta AB e abbiamo infinite circonferenze di raggio sempre diverso. Basta rappresentare tutte queste circonferenze su un piano e si vede immediatamente che la circonferenza di minima curvatura è proprio quella che ha il raggio uguale a quello della sfera, ossia che passa per il suo centro. Questa circonferenza è anche unica.

Ne segue che la distanza minima tra A e B viene misurata lungo un cerchio massimo e che esiste solo un cerchio massimo che passa per due punti, proprio come capita per una retta nella geometria euclidea. Si potrebbe anche fare una figura attraverso un programma raffinato e a questo punto avrebbe senso (come mostrato da Arturo Lorenzo nei commenti al quiz (QUI))

Ribadiamo ancora l’eleganza dello spazio sferico. Nello spazio euclideo rette e circonferenze sono due entità geometriche diverse (a parte il considerare un raggio infinito), mentre in quello sferico le rette sono particolari circonferenze, descrivibili con parametri finiti

A costo di essere pedante, fatemi ancora ripetere un concetto importante da non dimenticare mai nella trattazione della geometria sferica: le sue rette sono i cerchi massimi, ossia le intersezioni con qualsiasi piano passante per il centro e la superficie sferica. Sopra di loro si misurano le distanze minime tra due punti.  Le rette della superficie sferica non sono illimitate, dato che sono circonferenze, ma, a parte questo, i cerchi massimi possono essere considerati a tutti gli effetti l’equivalente della retta. Ricordiamolo molto bene!

Vediamo, in Fig. 6, una conseguenza IMPORTANTISSIMA di quanto appena detto. A destra abbiamo un triangolo APB che giace sul piano della figura. I suoi lati sono ovviamente segmenti di retta. Se considerassimo la figura PCD, con CD curvilineo, NON avremmo un triangolo, ma, ad esempio, un settore di cerchio o anche qualcosa di più complicato. Una conclusione analoga succede sulla superficie sferica, a sinistra. Un triangolo sferico deve avere dei lati intrinsecamente rettilinei, ossia archi di cerchi massimi. Ne segue che la figura PAB è un vero triangolo sferico (i suoi lati sono segmenti rettilinei intrinseci), mentre la figura PCD non è un triangolo, dato che CD è un tratto di circonferenza intrinseca, appartenendo a un cerchio minore.

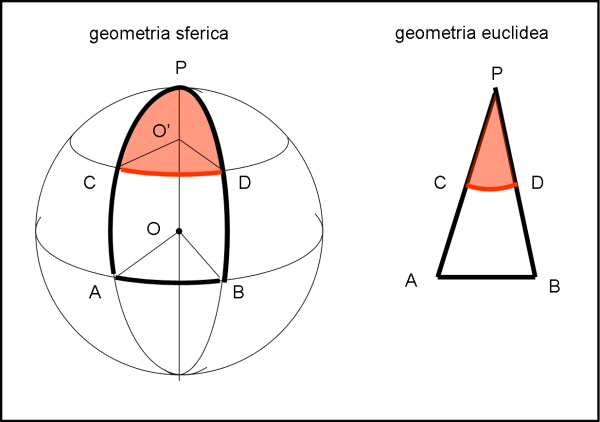
Quanto appena detto risponde in parte al quiz proposto QUI: qualsiasi percorso lungo un cerchio minore non può appartenere a un triangolo sferico. Per completare la soluzione ci serve, però, qualche altra considerazione che vedremo più in là.

Possiamo notare attraverso la Fig. 7, un’altra conseguenza da non dimenticare mai: la distanza minima tra due punti della superficie sferica viene descritta dal cerchio massimo che unisce i due punti, dato che rappresenta una geodetica, ossia il segmento intrinsecamente rettilineo. Qualsiasi altro cerchio minore che li congiunga è sicuramente più lungo, avendo una curvatura maggiore.

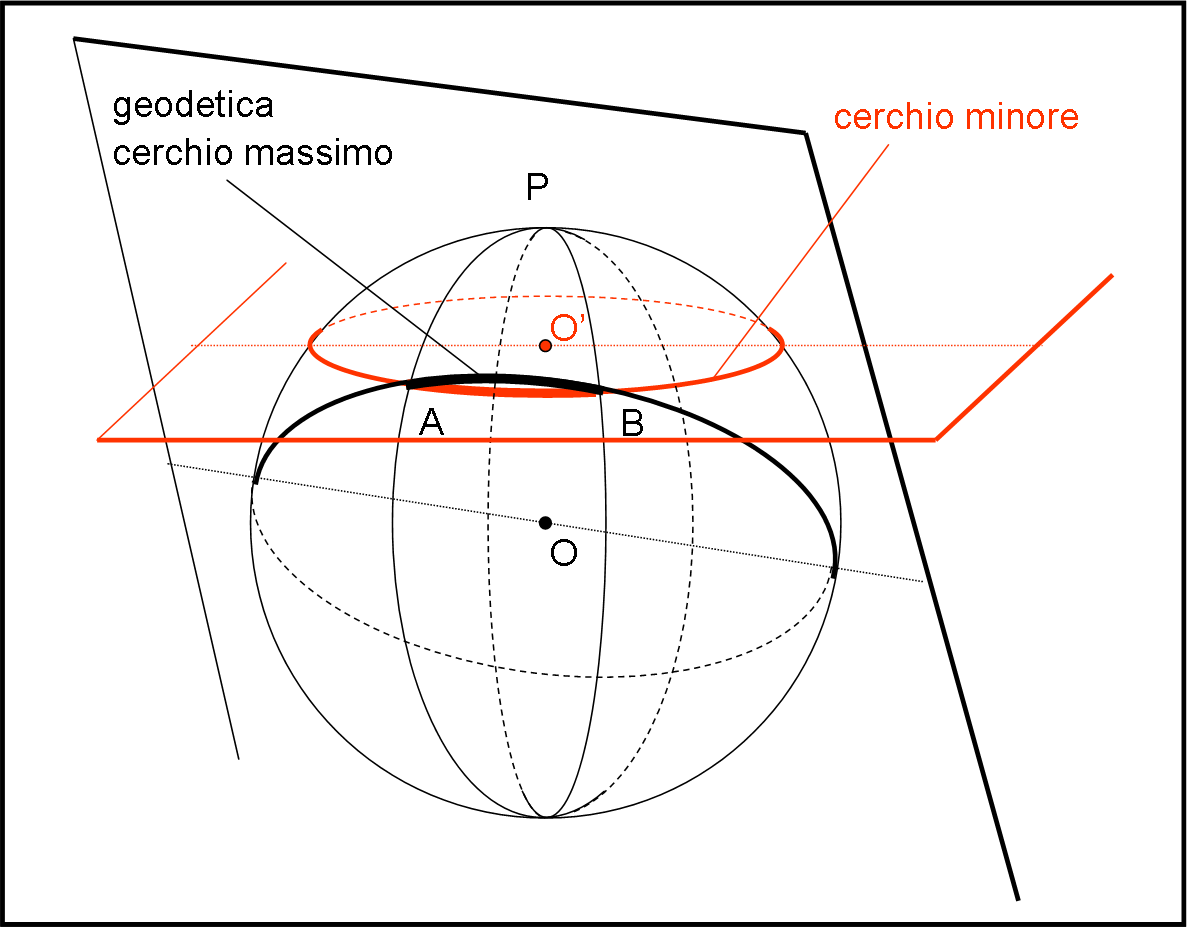
Abbiamo deciso di utilizzare la nostra capacità di vedere una superficie sferica in tre dimensioni e allora diamoci dentro, scoprendo un mucchio di cose veramente interessanti.

Tanto per cominciare partiamo dalla definizione di lato di un triangolo sferico. Poi passeremo ai suoi angoli.

Mettiamo, innanzitutto, in rilievo la differenza tra raggio di una circonferenza misurato sulla superficie sferica (intrinseco) e quello della stessa circonferenza misurato nello spazio con una dimensione in più (estrinseco). Vediamolo subito nella Fig. 8.

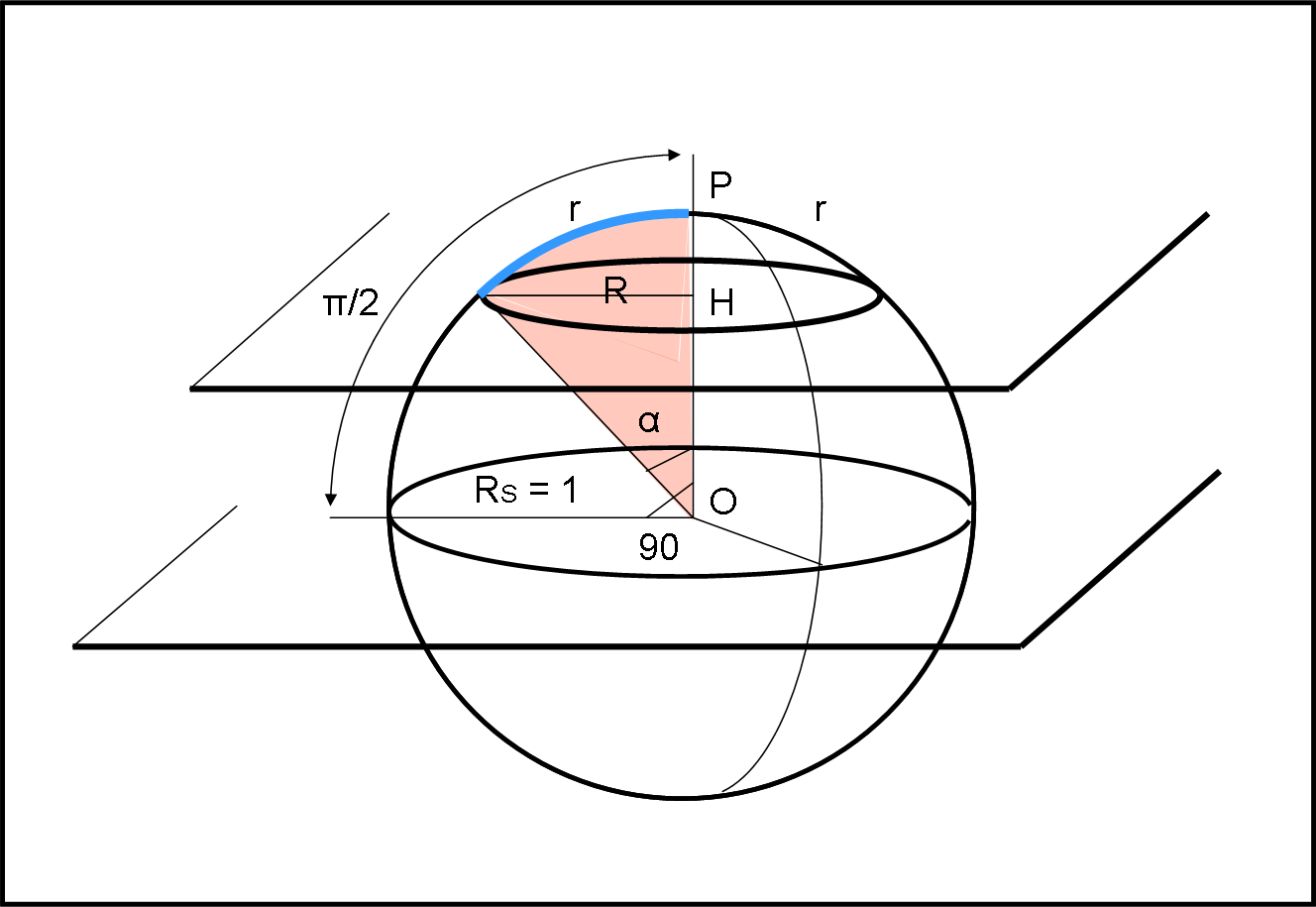
Per chi vive nel mondo sferico (sulla superficie) il raggio del cerchio, in alto, è r. Ma per chi può vedere la superficie dal di fuori, la stessa circonferenza ha un raggio nettamente minore, uguale a R. Ovviamente R esiste solo nel mondo a tre dimensioni e non può essere misurato direttamente da che vive sulla superficie sferica. La relazione tra i due raggi è banale, considerando, oltretutto, il raggio della sfera R_S uguale all’unità (come faremo sempre con la sfera celeste).

Abbiamo:

R = sin α

Vale, però, la proporzione:

r : 2π R_S= α : 360

r : 2π = α : 360

esprimendo α in radianti, abbiamo:

r : 2π = α : 2π

r = α                                        …. (1)

Da cui si può scrivere che

R = sin r

La banale relazione (1) è fondamentale nella sfera celeste in quanto definisce la misura di un arco di cerchio massimo, proprio ciò che diventa un lato di un triangolo sferico.

Anche il cerchio massimo può essere espresso in questi termini: il suo raggio intrinseco è uguale a π/2, mentre quello estrinseco è uguale a R_S = 1

Infatti, come dice la (1), abbiamo proprio

R_S = sin(π/2) = 1

Le “rette” intrinseche della superficie sferica sono le circonferenze di raggio intrinseco uguale a π/2, che corrispondono a un raggio estrinseco uguale all’unità. In altre parole, l’arco di cerchio massimo corrispondente a un angolo al centro di 90° è proprio uguale a π/2

Torniamo ai nostri triangoli sferici… Ribadiamo ancora il concetto base, ricordandoci che

un triangolo piano è formato da tre lati che sono dei segmenti rettilinei. Nel caso del triangolo sferico abbiamo, perciò, bisogno di tre segmenti di retta, ma le rette sono i cerchi massimi, e allora possiamo concludere che un triangolo sferico ha per lati tre segmenti di cerchio massimo (ovviamente minori di π).

Come si calcolino i segmenti di cerchio massimo l’abbiamo appena visto: essi non sono altro che gli archi di cerchio massimo, espressi in radianti, corrispondenti a un certo angolo al centro.

Possiamo perciò dire, per definizione di cerchio massimo, che:

 i triangoli sferici sono i triangoli generati sulla sfera dall’intersezione di 3 piani passanti per il centro della sfera stessa

ATTENZIONE: Chiediamoci sempre, prima di applicare le formule di trigonometria sferica che descriveremo di volta in volta, se i lati del triangolo che stiamo considerando sono realmente archi di cerchio massimo e non archi di cerchio minore. Se anche un solo lato non fosse arco di cerchio massimo, le formule non varrebbero più ed è come se volessimo applicare le formule euclidee relative  un triangolo piano, a una figura che ha un lato curvilineo.

Prima di concludere questa prima parte, pensate alle traiettorie degli aerei che sembrano percorre archi di cerchio lunghissimi per unire due città che sembrano molto più vicine se raggiunte attraverso una retta. Ebbene, l’apparenza inganna, dato che sulla cartina di volo si rappresenta la superficie sferica come un piano (i paralleli che non sono cerchi massimi sono spesso disegnati rettilinei) e quindi le vere distanza sono trasformate. La linea apparentemente curva è proprio la più breve.

Una cosa simile capita in uno spazio a tre o quattro dimensioni curvo, dove il percorso minimo non corrisponde alla nostra retta piana. Ed ecco servita su un piatto d’argento la relatività generale…

Scusate se sono stato ripetitivo e assillante, ma per poter utilizzare al meglio la trigonometria sferica è essenziale non confondere i veri triangoli sferici con i triangoli solo “apparenti”.

Bene. Abbiamo definito i lati di un triangolo sferico. Non ci resta che definirne anche gli angoli e poi, con calma, potremo divertirci con la trigonometria sferica…