Gli infiniti di Cantor-Parte dodicesima: Il teorema di Bernstein
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Stiamo affrontando un fase preparatoria ; dobbiamo introdurre uno strumento di confronto per semplificare alcune dimostrazioni sulla cardinalità degli insiemi. Quando andremo a confrontare insiemi come l'insieme delle parti di N con R, oppure R (retta euclidea) con R x R (piano euclideo) non sarà così facile trovare un corrispondenza biunivoca fra i due. La cosa più difficile in genere non è dimostrare che una corrispondenza sia iniettiva, ma dimostrarne la suriettività. C'è un metodo più semplice, dovuto a Bernstein. Riprendo prima una definizione usata precedentemente in altri articoli.
Confrontare la cardinalità di due insiemi
Vogliamo definire quando la cardinalità di un insieme X sia minore di quella di un insieme Y. Diremo che |X|<=|Y| se esiste una funzione iniettiva f di X in Y: f: X--->Y . Ma se fosse anche |Y|<=|X| ? Ovvero se esistesse una funzione iniettiva g di X in Y: g: Y--->X? Saremmo tentati di dire che |X|=|Y|, come faremmo con due numeri reali. Nel caso di due insiemi finiti A, B è abbastanza ovvia; se f:A--> B è iniettiva, manda punti distinti in punti distinti, quindi se indichiamo con a,b il numero di punti di A,B allora a<=b ; per lo stesso motivo, se c'è una g:B--> A iniettiva, b<=a, quindi a=b.
Nel caso di insiemi infiniti invece la dimostrazione non è banale e prende il nome di Teorema di Cantor-Bernstein , ed è stata realizzata da Felix Bernestein, che si dice sia stato allievo di Cantor e a cui Cantor affidò lo dimostrazione del teorema, essendo probabilmente già certo della soluzione.
Lemma preparatorio
Sia ; supponiamo che esista una applicazione biunivoca
f: Z--->X; allora esiste anche una applicazione biunivoca g di
g: Z---->Y
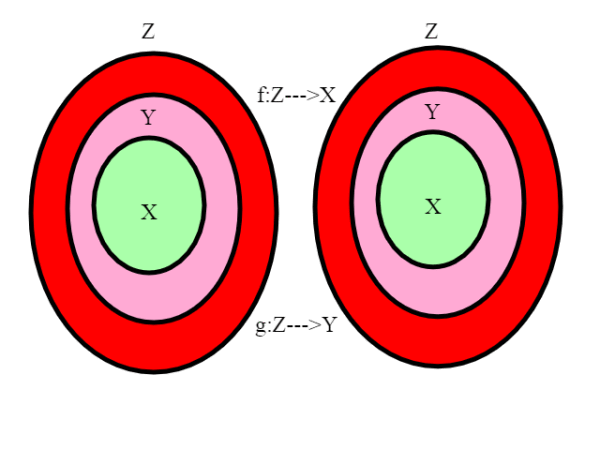
Osserviamo che questo è possibile solo se gli insiemi in gioco sono infiniti; infatti nel caso finito non può esistere una corrispondenza fra un insieme e un suo sottoinsieme proprio, ma nel caso infinito si (basta ricordare l'esempio di N e dei numeri pari). Sappiamo poi che ciò è possibile nel caso dei tre insiemi N,Z,Q. Vogliamo dimostrare che è vero nel caso generale di insiemi infiniti qualsiasi.
Dimostrazione del lemma preparatorio.
Poniamo Ao=Z-Y, ovvero la parte in rosso della figura qui sotto.
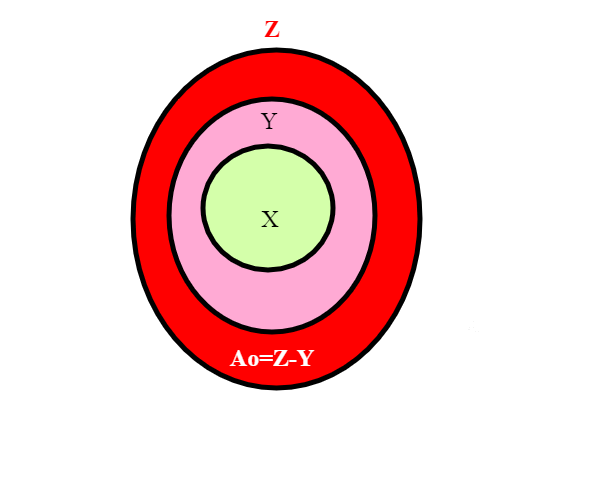
Definiamo una famiglia di insiemi in modo ricorsivo; A0=Z-Y,
A1=f(Ao) ;
A2=f(A1) ...
An=f(An-1);
An+1=f(An)
(non lasciatevi spaventare da questa definizione:è stata generata dall'intuito di un grande matemarico, vedremo in seguito a cosa serve)

osserviamo che A1,A2, ..An, An+1 sono sottoinsiemi di X, essendo f una applicazione di Z-->X
Chiamiamo ovvero l'unione di tutti gli An; possiamo anche dire che
quindi , ponendo
,
. f(A) risulta contenuta in X ( gli Ai sono tutti sottoinsiemi di X, quindi anche la loro unione è contenuta in X) e quindi anche in Y, essendo X sottoinsieme di Y;
. Notiamo poi che su
f è suriettiva; infatti comunque prendiamo un elemento in A, tale elemento apparterà a qualcuno degli Ai, ma ogni Ai è immagine di qualche altro elemento della famiglia di insiemi. A questo serve la definizione ricorsiva di A.
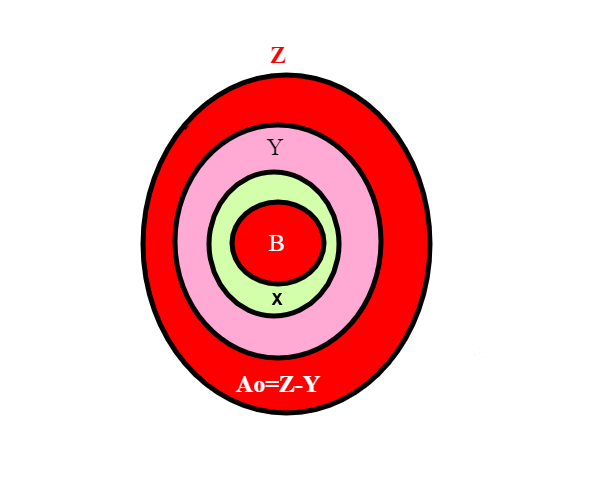
Costruiamo adesso una funzione di Z---> Y in questo modo: (la funzione f è definita su tutto Z e ha valori in X; dobbiamo in qualche modo estenderla perchè f non ha valori in Y, ma solo in X)
In questo modo riusciamo a coprire gli elementi della parte viola di Y.
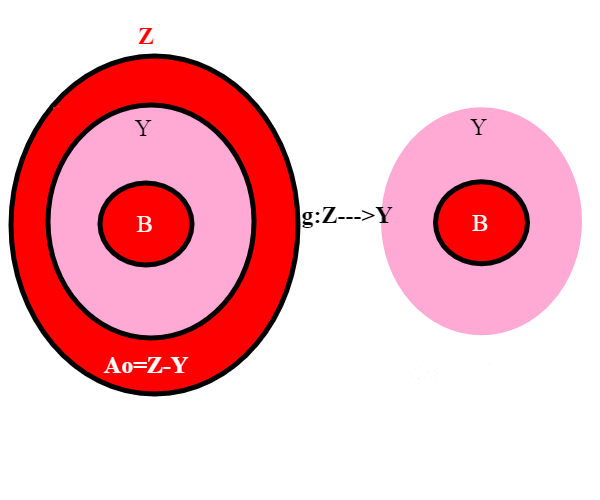
dimostriamo per prima cosa che g è iniettiva ;possiamo distinguere tre casi:
1) appartengano ad A; ma essendo g definita in tal caso interamente da f,
implica
;quindi
2) appartengono a Z-A,
; ma allora la definizione della funzione è:
;quindi
3) appartiene ad A ,
appartiene a Z-A ;
ma allora che appartiene ad A, essendo immagine di f di un elemento di A;
che appartiene a Z-A, ma allora
perchè
appartengono ad insiemi complementari.
Suriettività di g:
Se y appartiene a Y, allora o appartiene a Y-A, oppure appartiene ad A :

(ricordiamo la definizione di g: )
supponiamo che y appartenga a Y-A; allora g(y)=y perchè se non appartiene ad A sta in Z-A.
Se y appartiene Ad A (ovvero a B) allora essendo ; questo vuol dire che esiste un certo i per cui y appartiene ad
; ma per come sono definiti gli
(anzi, sono stati definiti apposta così) esiste z appartenente ad
tale che f(z)=y. ma dato che z appartiene ad A, g(z)=f(z)=y. (osserviamo che essendo n>1, al limite per i=0, troviamo che z sta in Ao)
Il Teorema di Cantor-Bernstein
Siano X e Y due insiemi e supponiamo che f:X--->Y e g:Y--> X siano due funzioni iniettive. Detto con il linguaggio dei numeri cardinali, |X|<=|Y|, |Y|<=|X|;
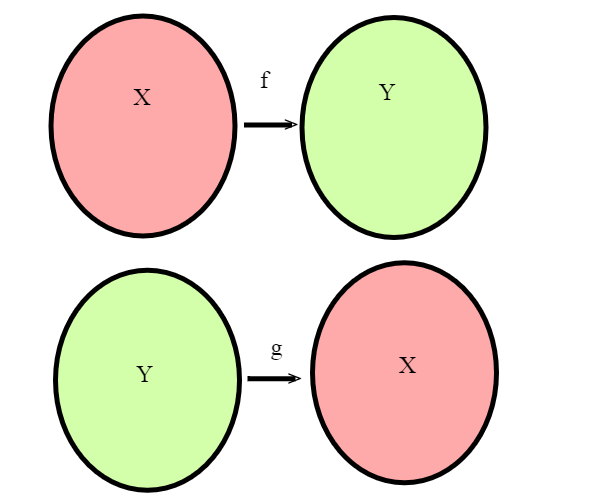
Allora esiste una funzione biettiva h:X---> Y, ovvero se |X|<=|Y|, |Y|<=|X| allora |X|=|Y|
Osserviamo che
1)|X|=|f(X)|, infatti f:X--->Y è iniettiva, ma considerando come codominio f(X) è anche suriettiva, quindi è una corrispondenza biunivoca.
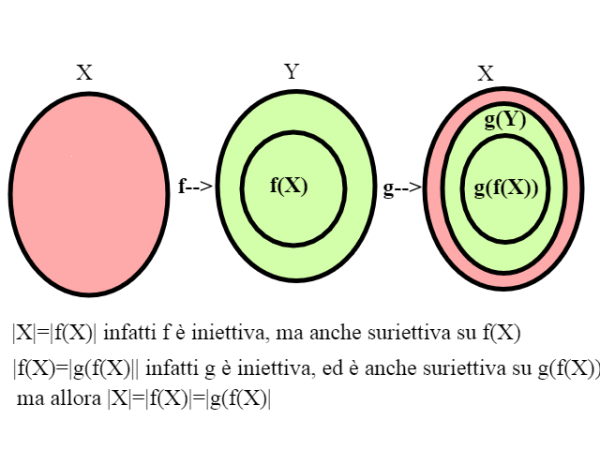
2) |f(X)=|g(f(X)|| infatti g è iniettiva, ed è anche suriettiva su g(f(X))
dal confronto fra 1) e 2) segue allora |X|=|f(X)|=|g(f(X)|; il fatto che |f(X)|=|g(f(X)| implica che esiste una applicazione biunivoca fra X e g(f(X).
essendo poi
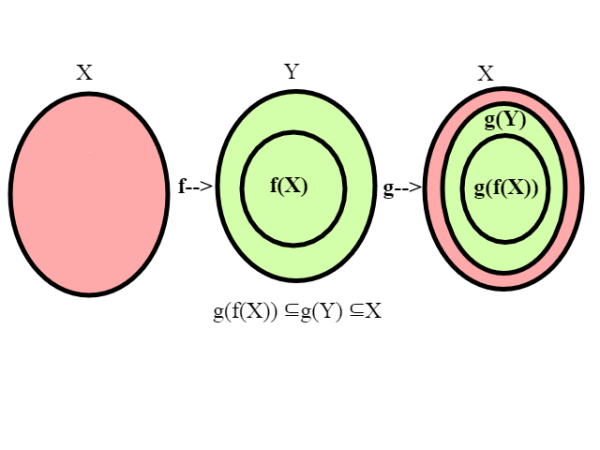
siamo nelle ipotesi del Lemma preparatorio; esiste una corrispondenza biunivoca fra X e g(f(X)) ma allora esiste anche una corrispondenza biunivoca fra X e g(Y). Ma dato che |g(Y)|=|Y| (g è iniettiva ma anche suriettiva su g(Y)) allora |X|=|g(Y))=|Y|.





