Questo articolo è stato inserito nella pagina d'archivio "Matematica e geometria" e in "Antichi Greci, che passione!"

 

L'immagine di copertina si capirà nel seguito. Per adesso, ci basti sapere che il numero 6 può essere sia GRANDE che PICCOLO... tutto dipende dai "sassolini" usati!

 

Per parlare dei numeri, non basterebbero tutti i libri esistenti al mondo. Essi non sono solo le lettere della matematica, ma molto, molto di più. La matematica (costruita da noi) usa i numeri, ma solitamente non s’interessa di cosa essi siano realmente e di come possano essere veramente descritti. Per capire meglio il loro mondo fantastico è necessario tornare all’antica Grecia (forse anche prima, ma i dati in nostro possesso sono troppo scarsi), in particolare alla scuola di Pitagora. Scopriremo un vero universo, pur limitandoci a poche nozioni. Scopriremo anche che la nostra tecnologia non è ancora riuscita a risolvere molti dei loro segreti. Chissà che un giorno i nostri Ciccio e Astericcio non decidano di fare un giro in questo mondo fantastico?!

 

Cosa sono i numeri?

A riguardo è molto indicativa la frase di Luca Pacioli, un religioso, economista e matematico del XV secolo, ma soprattutto un vero conoscitore dei numeri e della loro essenza:

“Ancora si comme fra la gente più imperfecti e tristi che buoni e perfecti si trovano e li buoni sono pochi e rari: così fra li numeri pochi e rari sono li perfecti e molti e assai sonno li imperfecti: cioè superflui e diminuiti”.

 Il mondo dei numeri è un mondo ben più complesso di quanto si pensi e non vi è nessun bisogno che essi siano veramente “complessi”, ossia facciano uso spudorato della radice quadrata di -1.  Il nostro modo di descriverli è veramente squallido e anonimo. Cosa direste infatti se, all’atto della vostra nascita, vi fosse stato affibbiato solo un codice più o meno numerico, del tipo PX112CF? Appena in grado di farlo, urlereste: “Non sono mica una targa di automobile o una bottiglia o una merce qualsiasi? Sono una donna/uomo, merito molto di più. Sono un essere vivente, con la mia personalità, le mie idee, le mie speranze, i miei desideri, i miei difetti. Un numero, ma siete matti?”

Ebbene, le stesse considerazioni valgono per i … numeri. Anche loro sembrano nascere nell’atto in cui li scrivete o li pronunciate. Un esempio? “234167432”. Cosa ho fatto? Ho scritto un numero qualsiasi, un freddo anonimo numero? No, assolutamente no! Ho fatto nascere una creatura con tutte le sue caratteristiche che lo rende diverso da un altro, ne fa un esemplare unico!

Mi potreste dire: “Su, per favore, un numero nasce e muore a nostro piacimento, e poi ce ne sono tanti, infiniti… come poter credere che ognuno abbia una sua spiccata personalità?”

Mamma mia… non fatevi sentire da un elettrone o da un fotone… per cortesia. Anche loro sono praticamente infiniti e apparentemente tutti uguali tra loro, ma provate a chiamarli con un simbolo, un “numero” o un codice e sareste attaccati da una sequela di processi quantistici che vi distruggerebbero in un attimo. Loro sono buoni e cari, ma ricordate sempre che sono le uniche creature capaci di avvisarsi attraverso l’entanglement, un’informazione che fa apparire la luce una tartaruga, quasi imbarazzante nella sua lentezza.

Gli esempi sarebbero moltissimi e quindi fermiamoci pure: ne usciremmo sempre più sconfitti e appariremmo dei presuntuosi ignoranti. In fondo, lo sappiamo benissimo che non siamo noi a usare i numeri, ma sono loro che cercano di aiutare le nostre limitate potenzialità deduttive e interpretative attraverso ciò che noi chiamiamo matematica.  La matematica non è il mondo dei numeri, ma solo un linguaggio semplice che i numeri ci hanno concesso per avere solo una pallida idea del loro mondo.

Torniamo, perciò alla frase di Pacioli, uno che aveva capito molte cose, non per niente era amico di Leonardo da Vinci.

Come ci sono fotoni più o meno energetici così ci sono numeri più o meno importanti, potenti e conosciuti. Tuttavia, non pensiamo certo che mettere insieme le poche cifre che noi riteniamo fondamentali, da 0 a 9, sia capire l’essenza dei numeri. Nemmeno per sogno… quelle cifre le abbiamo create noi per riuscire a scriverli in qualche modo, ma loro esistono indipendentemente dalle nostre limitate capacità descrittive. Non è molto che abbiamo incontrato un alieno che usa cifre diverse per scrivere un numero. Non confondiamo quindi la cifra, un simbolo che abbiamo deciso noi, con un numero, un qualcosa di immutabile e unico.

Gli antichi greci l’avevano intuito e non per niente usavano figure geometriche per crearli, per farli giocare tra di loro, per accattivarseli e per cercare di carpirne qualche segreto. Poi, la modernità delle cifre ha sveltito i nostri squallidi calcoli e ci ha fatto credere di averli domati e di poterli trattare come oggetti senz’anima, adattabili ai nostri scopi intellettuali o scientifici.

Un po’ come capita alle parole che non sono certo un insieme di lettere, ma rappresentano qualcosa di ben più universale. Se scrivete “pane” vi riferite a qualcosa di specifico, di preciso, di reale. E, invece, se dite “quarantuno” pensate solo a quaranta volte uno e non a un’entità  che vive una sua vita indipendente e non certo banale.

C’è forse una vera differenza tra XLI romano e 41 arabo occidentalizzato?  E, allora, tanto vale mettere 41 sassolini uno a fianco dell’altro. Sareste decisamente più vicini alla realtà del mondo dei numeri. Così facevano i greci e probabilmente anche le civiltà più antiche, ben più vicine alla splendida realtà del Cosmo di quanto non lo siamo noi oggi schiavi dei calcolatori e di un’elettronica dominata dalle particelle quantistiche. Sono loro che si servono di noi per vivere le loro avventure e non certo il viceversa!

Numeri e sassolini

Torniamo a Pitagora e ai suoi seguaci. In particolare soffermiamoci su un nome molto difficile, ma di semplice comprensione: Aritmogeometria. Il suo significato non è altro che quello di rappresentare i numeri naturali (interi positivi) attraverso configurazioni geometriche di punti (o sassolini, se preferite).

Non cominciate, però, a dire che Pitagora era limitato, in quanto usava solo i numeri positivi… I numeri negativi non sono altro che uguali e opposti, ma difficilmente rappresentabili geometricamente.

Ridete di lui? Pensate all’antimateria e provate a costruirla a casa vostra, se ne siate capaci. Quanti vorrebbero costruire un’antisuocera e annichilire la propria suocera, ma nessuno c’è ancora riuscito! Bene, possiamo pensare che i numeri negativi siano gli antinumeri positivi. D’altra parte mettere quattro sassolini e poi toglierli subito, non è come annichilire un elettrone e un positrone? Il risultato è sempre zero e … non parlate di energia, dato che nessuno sa ancora misurare l’energia che deriva dai numeri e dalla loro annichilazione.

Ancora una volta, abbiamo visto l’estrema somiglianza tra i numeri e le particelle quantistiche. I veri padroni dell’Universo. Provate a costruire un presidente e un antipresidente. Faranno di tutto per annichilirsi, ma mai riusciranno a sparire del tutto, anzi o ne sparisce uno solo o si metteranno d’accordo! L’essere umano è nettamente più limitato, non c’è dubbio…

Diceva Diogene di Laerzio riguardo ai pitagorici: “I numeri apparivano a loro primi tra tutto ciò che è nella natura; pensavano che gli elementi dei numeri fossero elementi di tutte le cose che sono, e che l’intero mondo fosse armonia e numero”.

Per non parlare di Aristotele: “I Pitagorici dicono che da numeri sono composte le sostanze percepibili. … Essi dicono che il numero è le cose che sono, o almeno applicano i loro teoremi ai corpi, come se i numeri fossero dei corpi”.

Alcuni esempi classici:

Il numero 1 rappresenta il principio di tutto, la ragione. In geometria è il punto o il sassolino.

Il numero 2 rappresenta la parte femminile, l’indefinito, l’opinione. In geometria è la linea.

Il numero 3 rappresenta la parte maschile, ciò che è definito e limitato. Geometricamente è il piano.

Il numero 4 è la giustizia, dato che può essere diviso con equità in due parti.

In numero 5 è il matrimonio (unione di 2 e 3)

Il numero 10 è la sintesi dell’Universo, dato che contiene l’inizio, la parte maschile, la parte femminile e la giustizia che lo domina. La sua rappresentazione geometrica è un triangolo equilatero di lato 4

Malgrado i dubbi e le velate prese in giro, i pitagorici riuscirono ad avere un colloquio diretto con i numeri e a sapere, almeno in piccola parte, il loro vero significato. Seppero che loro avevano gerarchie molto complicate e che vi erano numeri buoni, numeri cattivi, numeri timidi e numeri ambiziosi. Un mondo intricato e complesso, di cui ancora oggi conosciamo ben poco.

D’ora in poi useremo le nostre cifre per farci capire, ma ricordiamoci che stiamo usando solo sassolini e figure geometriche.

I numeri poligonali

Torniamo, quindi, a Pitagora e cerchiamo di conoscere i suoi numeri geometrici o, più esattamente, poligonali. Si potrebbe fare molto di più, ovviamente, ma dare a ogni numero una sua forma geometrica e un suo modo preciso e rigoroso di procreare e moltiplicarsi è già un passo in avanti verso la loro conoscenza…

Prendiamo un esempio banalissimo: i numeri triangolari (1, 3, 6, 10, …), che vediamo in Fig. 1.

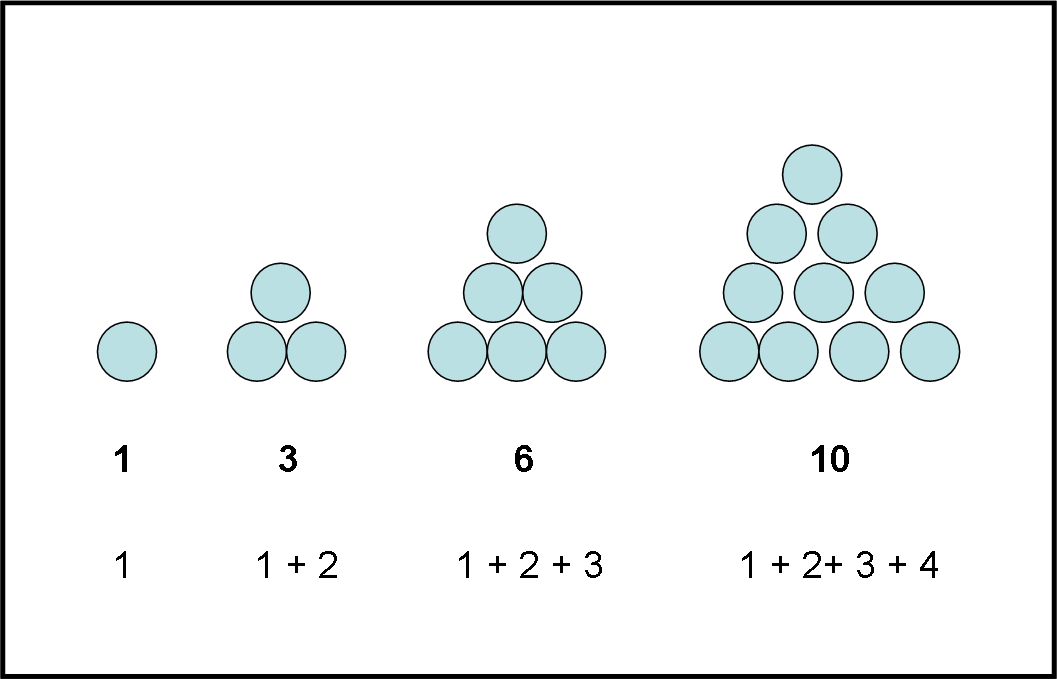
Numeri qualsiasi per noi, ma non certo per loro. Proviamo a sommare i numeri cominciando da 1.

1

1 + 2 = 3

1 + 2 + 3 = 6

1 + 2 + 3 + 4= 10

Lo schema vuole dire che il primo numero triangolare è 1, il secondo è 3, il terzo è 6, il quarto è 10, e via dicendo.

Ogni volta che aggiungiamo il numero intero successivo otteniamo un nuovo numero triangolare. Oggi diremmo che per ottenere un qualsiasi numero triangolare (l’ennesimo numero triangolare) basta sommare tutti i numeri fino al valore n cercato e scrivere:

Tn= 1 + 2 + 3 + 4 + …. +  n = n(n+1)/2   (serie di Gauss, ma vedremo che se ne può fare a meno)     …. (1)

In altre parole, molto più pratiche: per ottenere il decimo numero triangolare, basta sommare tutti i numeri da 1 a 10, ossia 1 + 2 + 3 + …. + 9  + 10 = 55

Così come abbiamo introdotto i numeri triangolari, possiamo andare avanti come hanno fatto i pitagorici. Ad esempio con i numeri quadrati. La loro descrizione è semplice (Fig. 2).

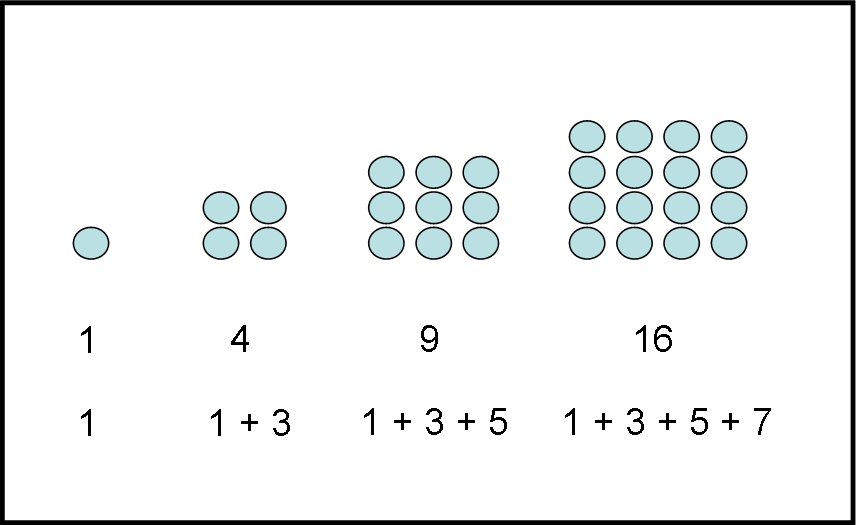
Essi sono:

1, 4, 9, 16, 25, …

Ovviamente sono tutti… quadrati di qualche numero, per costruzione. Il secondo è il quadrato di 2, il terzo è il quadrato di 3 e via dicendo.

Ma essi ci dicono cose molto importanti che li legano ai numeri triangolari e non solo..

Ad esempio, un numero quadrato è sempre uguale alla somma di un numero triangolare e di quello successivo. La faccenda si nota immediatamente dalla Fig. 3, dove i numeri triangolari consecutivi sono identificati con sassolini di colore diverso.

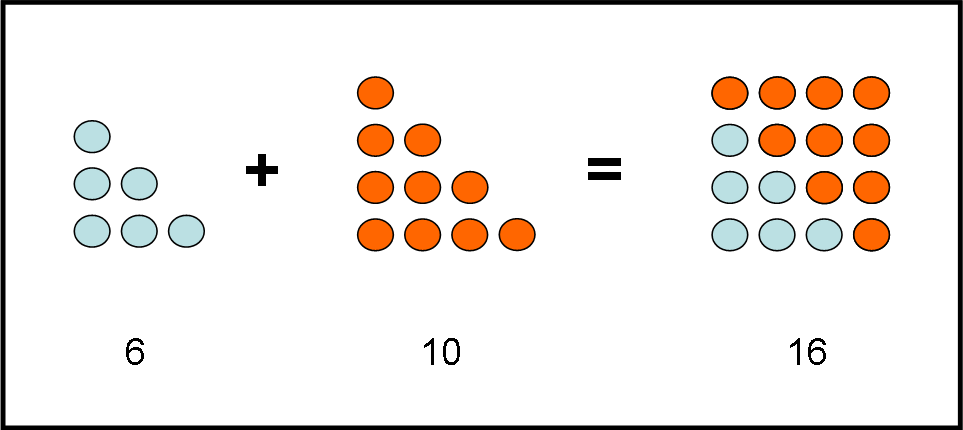
Se non crediamo alla figura, possiamo sempre usare le formule che ci siamo inventati in seguito:

il numero triangolare Tn è dato da:

Tn = 1 + 2 + 3 +… + n

Il numero triangolare T(n - 1) (quello precedente) è dato da:

T(n - 1) = 1 + 2 + 3 +… + (n - 1)

Ma la (1) ci dice anche che:

Tn = n (n + 1)/2

T(n-1) = (n - 1) n /2

Sommando:

Tn + T (n-1) = (n² + n + n² –n)/2 = n²

Bella forza! Ma niente di nuovo rispetto ai pitagorici… Sembra, infatti, che si sia dovuto usare una formula “moderna”. Nemmeno per sogno… la formula (1) si ricava facilmente usando la sola geometria. Lo vediamo in Fig. 4.

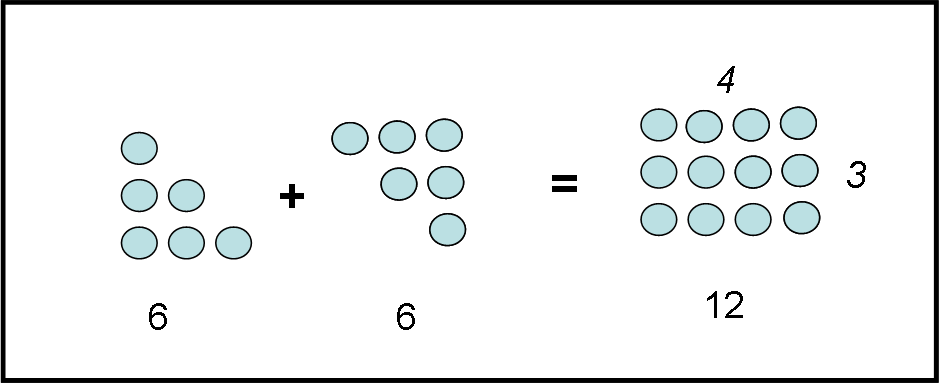
Prendiamo un numero triangolare Tn e gli accostiamo un altro numero triangolare Tn. La figura finale è un rettangolo di lati n e n+1, per cui deve contenere n (n + 1) punti (basta contare i sassolini). Ma questo numero è proprio il doppio dei numeri di un solo triangolo, ossia :

n(n+1) = 2Tn

da cui

Tn = n(n+1)/2

Con buona pace di Gauss…

Possiamo, però, svelare altri piccoli segreti, con i nostri sassolini, e avvicinarci anche alle prime misure astronomiche.

Prendiamo un bel numero quadrato e sottraiamogli il numero quadrato precedente (Fig. 5).

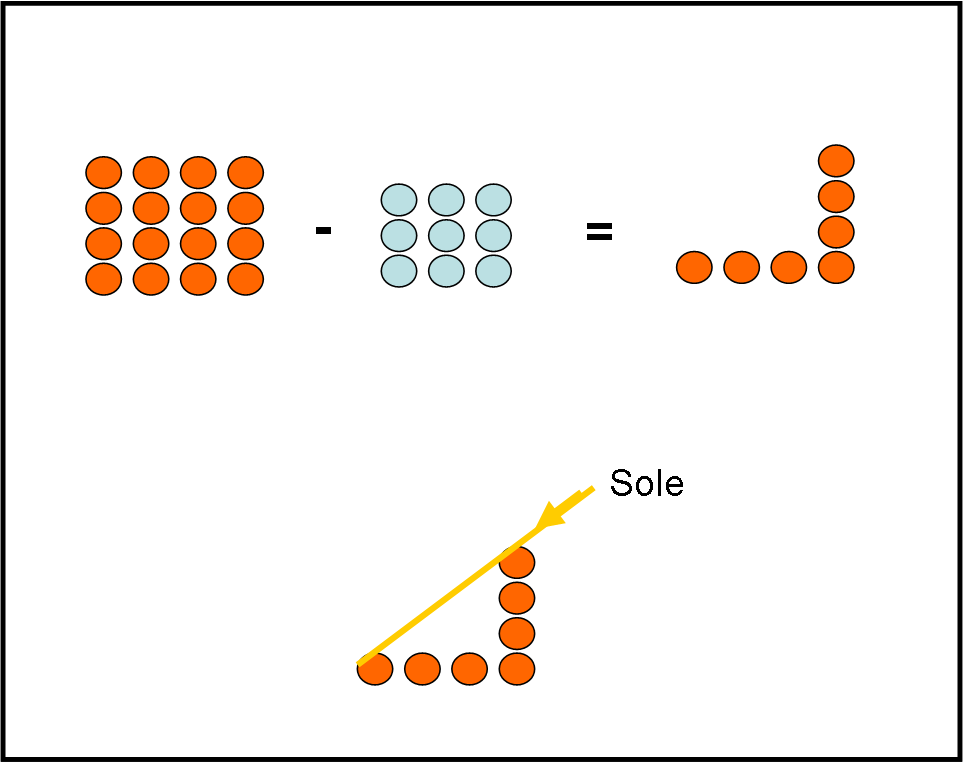
Cosa si ottiene? Una strana figura a L rovesciata orizzontalmente. Bene questa figura prende il nome di gnomone, ossia lo strumento base per tante misure, compresa quella della circonferenza della Terra (come fa è riuscito a fare Eratostene di Cirene nel III secolo a.C.). Essa simboleggia proprio un asta rigida con la sua ombra. Fantastico, veramente fantastico.

Vale anche il viceversa, ovviamente… Ossia, prendiamo il numero quadrato 4 (quattro sassolini). Aggiungiamogli lo gnomone relativo che è formato da 5 sassolini. Otteniamo il numero quadrato successivo, ossia 9. Abbiamo ripetuto quanto detto prima sottraendo da 9 il quadrato precedente, ossia 4, e ottenendo proprio 5, lo gnomone.

La faccenda si può scrivere in formule moderne, come:

(n + 1)² – n² =  n² + 1 + 2n – n² = 2n + 1     dove, nel caso precedente, n vale 2.

Infatti, il quadrato di due è proprio il numero quadrato 4, il quadrato di n + 1 = 3 è proprio il numero quadrato 9. Lo gnomone corrispondente è 2 ∙ 2 + 1 = 5.

In altre parole, abbiamo detto che per ottenere il numero quadrato successivo basta aggiungere lo gnomone corrispondente. Spieghiamoci meglio…

Prendiamo il primo numero quadrato, ossia 1. Aggiungiamo il suo gnomone che è  (2n + 1), ossia 2 ∙ 1 + 1 = 3 e otteniamo il secondo numero quadrato che è 4. Aggiungiamo a questo lo gnomone relativo che è 2n + 1 = 2 ∙ 2 + 1 = 5. Otteniamo il terzo numero quadrato 9. Prendiamo il suo gnomone che è 3 ∙ 2 + 1 = 7, lo sommiamo e otteniamo il quarto numero quadrato che è 16.

In parole molto povere, per ottenete il numero quadrato Qn basta sommare tutti i numeri dispari (ossia gli gnomoni). In parole “matematiche”:

Qn = 1 + 3 + 5 + 7 + 9 + … + (2n -1)        somma dei numeri dispari

Per ottenere il quarto (n =4), basta sommare 1 + 3 + 5 + 7 = 16    (7 è proprio 2n -1)

Per ottenere il quinto (n = 5), basta sommare 1 + 3 + 5 + 7 + 9 = 25    (9 è proprio 2n -1)

Insomma, gli gnomoni (i numeri dispari) servono sia a scrivere tutti i numeri quadrati, ma anche a misurare la circonferenza della Terra. Se non è una prova dell’importanza del mondo dei numeri questa…!

Ovviamente, i pitagorici sono andati avanti con i numeri poligonali, trovando relazioni sempre più complicate e generali, ma noi possiamo fermarci e prendere un’altra direzione, quella della perfezione. Per gli amanti dei numeri, però, abbiamo dato tanti spunti per entrare sempre più in questo mondo fantastico (e bastano solo dei sassolini o, se preferite, dei punti disegnati su un foglio). Provate con i pentagoni, gli esagoni e potrete scoprire proprietà fantastiche.

Non tutti sono perfetti

Costruendo un numero in forma geometrica non è difficile ottenere facilmente i suoi divisori, ossia i numeri che sono contenuti, nel numero in questione, un numero intero di volte. Un legame molto profondo e reciproco. Prendiamo il numero 8. Esso può essere ottenuto prendendo il due quattro volte oppure prendendo il quattro due volte. Ovviamente, 1 è un divisore di tutti i numeri, così come lo stesso numero. Quest’ultimo però non viene considerato come divisore, nella ricerca del carattere profondo dei numeri.

I divisori diventano molto importanti sommandoli tra di loro. Proviamo con quelli di 8 (1, 2, 4) …

1 + 2 + 4 = 7

Proviamo con quelli di 10 (1, 2, 5) …

1 + 2 + 5 = 8

Cosa ci dicono questi risultati? I numeri 8 e 10 sono numeri difettivi, ossia sono quelli del tipo “vorrei, ma non posso”. Fanno di tutto affinché la somma dei loro divisori sia uguale proprio al numero, ma non ci riescono, a volte per pochissimo. Sono numeri un po’ tristi, a cui manca qualcosa per raggiungere un posto di rilievo.

Proviamo con il numero 12

1 + 2 + 3 + 4 + 6 = 16

Accidenti… quanta arroganza! E’ del tipo “meglio esagerare sempre”. Sono numeri per cui la somma dei divisori è maggiore del numero e si chiamano eccedenti o abbondanti. Personaggi di cui fidarsi poco, troppo ambiziosi e pericolosi.

Pensate che Nicodoco (vissuto nel I secolo dopo Cristo) ne dà una descrizione ben più severa: i numeri difettivi sono creature malate, infelici, prive di qualche parte importante, come un cane cieco. I numeri eccedenti, invece, abusano degli altri, sono violenti, come mostri con molte file di denti.

Che siano veramente privi di regole lo dimostra un fatto piuttosto interessante. Esistono moltissimi numeri leggermente difettivi, ossia i cui divisori, se sommati, hanno solo un’unità di differenza dal numero, proprio come il numero 8, i cui divisori arrivano solo fino a 7. Invece, non esistono numeri lievemente eccedenti, ossia per cui la somma dei divisori sia solo di un’unità maggiore del numero.

Fermiamoci un attimo. L’ultima asserzione è del tutto ipotetica: ad oggi non è ancora stato trovato, malgrado i computer, un numero lievemente eccedenti, ma non vi è niente che dimostri che non possa esistere! Il mondo “reale” dei numeri è ancora pieno di misteri, non ancora svelati.

Universo o Universi dei numeri ?

Sarebbe ora di passare ai numeri perfetti, ma mi sono accorto (e qui c’è molto di soggettivo, ovviamente) che l’Universo dei Numeri può essere decisamente più complesso di quello che siamo abituati a guardare con il telescopio o ipotizzare con le formule… Probabilmente unisce in lui (o in loro?) sia i fenomeni più classici della meccanica quantistica che una struttura multi dimensionale, rispetto alla quale noi siamo decisamente più indietro.

Voglio scrivere una provocazione: quando conosceremo molto meglio il mondo dei numeri, proseguendo lungo le linee aperte dai grandi scienziati antichi, forse capiremo molto di più del vero spaziotempo in cui viviamo. Calco ancora più la mano: l’applicazione degli schemi matematici, attraverso formule sintetiche, potrebbe avere interrotto la strada più rapida verso la conoscenza TOTALE.

Non ridete, ma non prendetemi nemmeno troppo sul serio … certi pensieri e certe riflessioni devono essere discusse e confrontate. Quindi, prima di gettare al macero queste idee così “vagabonde” proviamo, tutti assieme, di ragionarci sopra. Al limite ci saremo divertiti un po’…

Vorrei, innanzitutto, arrivare a una visione quantistica dell’Universo dei numeri “figurati”, ossia quelli poligonali, formati da tanti sassolini o tanti punti o -ancora- da tante particelle minutissime. Non voglio nemmeno toccare la disposizione atomica nelle molecole o cose del genere che ci porterebbero nel mondo della chimica, in cui i numeri figurati la fanno sicuramente da padroni. No, mi basta restare alla definizione dei numeri poligonali e poco di più. Sveleremo mondi sconosciuti e, al momento, inavvicinabili.

Scriviamo i nostri numeri interi positivi uno dietro l’altro, ricordando che usiamo le cifre solo per facilità di scrittura: in realtà stiamo mettendo sassolini vicini tra loro.

Ora divertiamoci a sommare i numeri, come abbiamo fatto la volta scorsa:

1

1 + 2 = 3

1 + 2 + 3 = 6

1 + 2 + 3 + 4 = 10

Possiamo fare la stessa cosa, ricordandoci di volta in vola la somma precedente:

1

1 + 2 = 3

3 + 3 = 6

6 + 4 = 10

Otteniamo, ovviamente lo stesso risultato…. Tuttavia, questo secondo “metodo” ci permette di rappresentare l’operazione svolta attraverso la Fig. 6a.

Partiamo dalla prima riga dove ci sono tutti i numeri naturali. Riportiamo nella riga sotto il numero 1, l’origine di tutto, il numero che comanda tutti gli altri, la particella unitaria, il niente e il tutto, (il Big Bang…?).

Iniziamo a costruire, nella seconda riga, gli attori del “primo” Universo… sommiamo il primo numero della seconda riga (1) con il secondo della prima riga, ossia 1 + 2 = 3. Il risultato lo scriviamo come secondo numero della seconda riga. Prendiamo questo numero e sommiamolo con quello successivo della prima riga: 3 + 3 = 6. Scriviamolo e andiamo avanti con le somme e con la costruzione della seconda riga.

Beh… quello che abbiamo fatto è semplicissimo: abbiamo costruito la serie dei numeri TRIANGOLARI. Niente di nuovo, ovviamente. Tuttavia, possiamo considerare questi numeri -o agglomerati di particelle- gli attori di un particolare Universo in cui i personaggi si fanno via via più complessi pur seguendo sempre la stessa legge. Permettetemi di chiamarlo Universo Numerico Triangolare (UNT). I suoi abitanti hanno una caratteristica comune, quella di formare SEMPRE un triangolo equilatero.

Ricominciamo dall’inizio con la serie dei numeri… (Fig. 6b). Questa volta, però, ne cancelliamo uno no e uno sì. Ossia cancelliamo il 2, il 4, il 6, l’8, ecc. In poche parole, consideriamo i numeri dispari.

Seguiamo la legge operativa precedente. Sommiamo il primo numero (1) della seconda riga con il primo numero NON cancellato della prima riga (il 3). Abbiamo 1 + 3 = 4. Riportiamolo nella seconda riga . Prendiamo proprio lui e sommiamolo al numero successivo della prima linea (non cancellato, ovviamente). Abbiamo 4 + 5 (il 4 della prima riga è stato cancellato) = 9. Riportiamolo nella seconda riga e andiamo avanti con l’operazione che ormai conosciamo molto bene. Cosa otteniamo? Beh… lo sappiamo già dalla volta scorsa: i numeri QUADRATI. L’altra volta li avevamo trovati sommando i numeri dispari e, infatti, abbiamo operato in modo del tutto simile. Possiamo dire di avere costruito un secondo Universo, quello quadrato, l’Universo Numerico Quadrato (UNQ).

No, non ridete ancora… So benissimo che basterebbe fare una moltiplicazione o utilizzare un simbolo matematico. Lasciatemi proseguire in questo gioco da fanciulli, in cui sappiamo solo aggiungere sassolini…

Riprendiamo la solita serie dei numeri (Fig. 6c) e, dopo l’1, cancelliamo due numeri consecutivi. Nella seconda riga si mette sempre l’1 e poi lo si somma con il primo numero non cancellato, che questa volta è il 4. La somma è 5 e possiamo riportarlo nella seconda riga. Prendiamo il 5 e lo sommiamo con il successivo numero non cancellato, che è il 7. Otteniamo 12. Andando avanti troviamo il 22 e via dicendo.

Bene la serie 1, 5, 12, 22 non è altro che un nuovo Universo. Stiamo solo attenti a NON RIEMPIRE la figura ottenuta (il pentagono) e costruiamo il pentagono successivo, prolungando i lati di quello precedente. La figura illustra bene l’operazione. Non ho nemmeno bisogno di dirlo… ma abbiamo costruito l’Universo Numerico Pentagonale (UNP).

Passiamo alla Fig. 7 (ormai avete capito il procedimento), dove abbiamo cancellato tre numeri consecutivi.

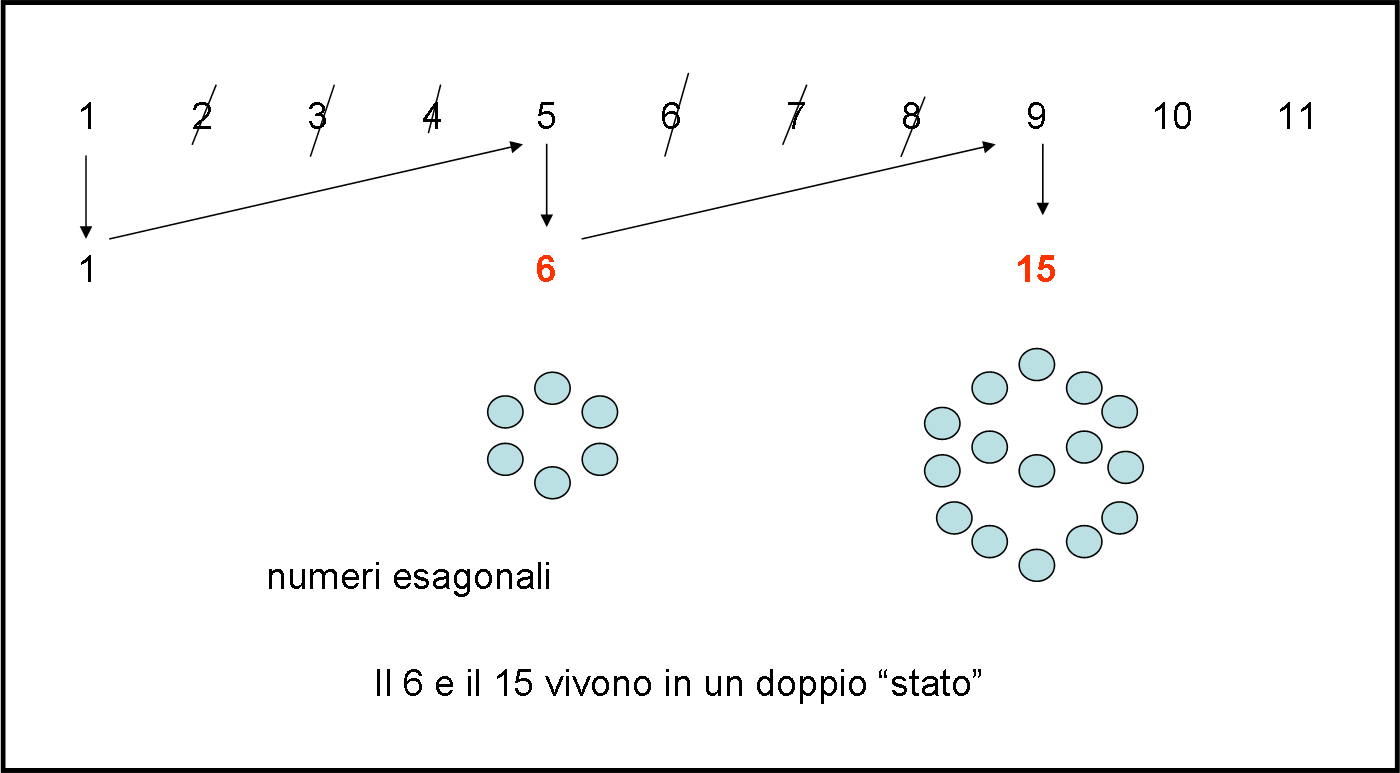
Ripetiamo la solita trafila 1 + 5 = 6; 6 + 9 = 15; ecc., ecc. I sassolini che si vedono sotto ai numeri della seconda riga la dicono lunga: sono esagoni, costruiti sempre prolungando i lati e senza riempire tutta la figura. Bene, potete dirlo da soli, abbiamo in mano l’Universo Numerico Esagonale (UNE).

Potremmo andare avanti all’infinito e avremmo infiniti Universi. Possiamo fermarci e riflettere. Tutti questi Universi sono sicuramente collegati tra loro, ma possono vivere indipendentemente. Le formule matematiche li legherebbero facilmente con cento strategie più o meno sofisticate. Ma a noi non interessa. Noi, per il momento almeno, abbiamo di fronte Universi paralleli (o quasi) in cui, però, certi numeri cominciano ad appartenere a più di un Universo. Ad esempio il 6 e il 15 e tutti quelli esagonali appartengono anche all’Universo triangolare. No, non ditemi: “Grazie… basta moltiplicare per due…” . Noi non siamo interessati alla moltiplicazione, operazione matematica che vogliamo far finta di non conoscere.

Bene.. posso permettermi di dire che il numero 6, il 15 e i loro compagni vivono in un doppio stato, ossia appartengono contemporaneamente a due Universi distinti. A seconda di come li raffiguro li faccio collassare in un Universo diverso.

Non fatemi proseguire con gli esempi… più andiamo avanti con la nostra operazione ripetitiva e più avremo numeri che appartengono a più stati e molte altre cose. Sì, sì, forse ho solo scherzato, ma quel numero 6 (che incontreremo ancora) ha acquistato un qualcosa di magico, così come quei sassolini o particelle che compongono i numeri a seconda dell’Universo in cui si possono sistemare.

Bisognerebbe studiare molto meglio i numeri figurati… quanto potrebbero insegnarci!

Fino a questo punto, però, abbiamo lavorato in un piano a due dimensioni (trascuriamo il volume dei sassolini) in cui compaiono tutti i poligoni che possiamo immaginare e che riusciamo a disegnare su un foglio. Tanti Universi bidimensionali…

Universi a più dimensioni

Cerchiamo di andare un po’ più avanti e sfruttiamo un teorema enunciato dal geniale matematico Moessner nel 1951. Non è molto diverso da quanto abbiamo fatto precedentemente, ma è necessaria molta attenzione. In fondo, è solo un gioco da bambini (dovete, però, avere a disposizione un bel mucchio di sassolini e … tanta fantasia.

Partiamo di nuovo con la solita serie dei numeri interi. Il primo passo è quello eliminare un numero sì e uno no. In altre parole, eliminiamo il secondo numero, poi il quarto e via dicendo. Come abbiamo visto si ottengono i numeri quadrati (Fig. 6b).

Riprendiamo la serie completa ed eliminiamo, adesso, il terzo, il sesto e via dicendo (due li teniamo e uno lo eliminiamo). Seguendo il solito procedimento di sommare e riportare in seconda riga abbiamo adesso una strana serie che ci dice ben poco (Fig. 8).

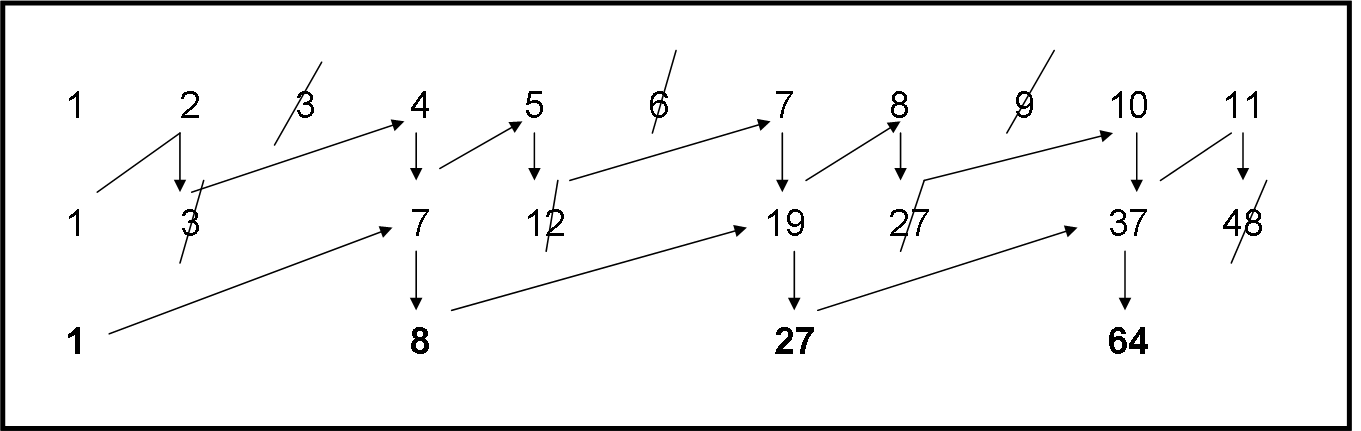
Non occupiamocene, anche se sicuramente ha una sua logica: non possiamo scoprire l’interno Universo, o -meglio- gli infiniti Universi “a due dimensioni”, in un colpo solo… Calma e sangue freddo. Teniamoci la nuova serie. Su di lei operiamo come fatto per trovare i quadrati, ossia, eliminiamo un numero sì e uno no… Fatto?

Bene,  abbiamo ottenuto una nuova serie di numeri: 1, 8, 27, 64, …

Non discutiamone ancora e proseguiamo con la Fig. 9.

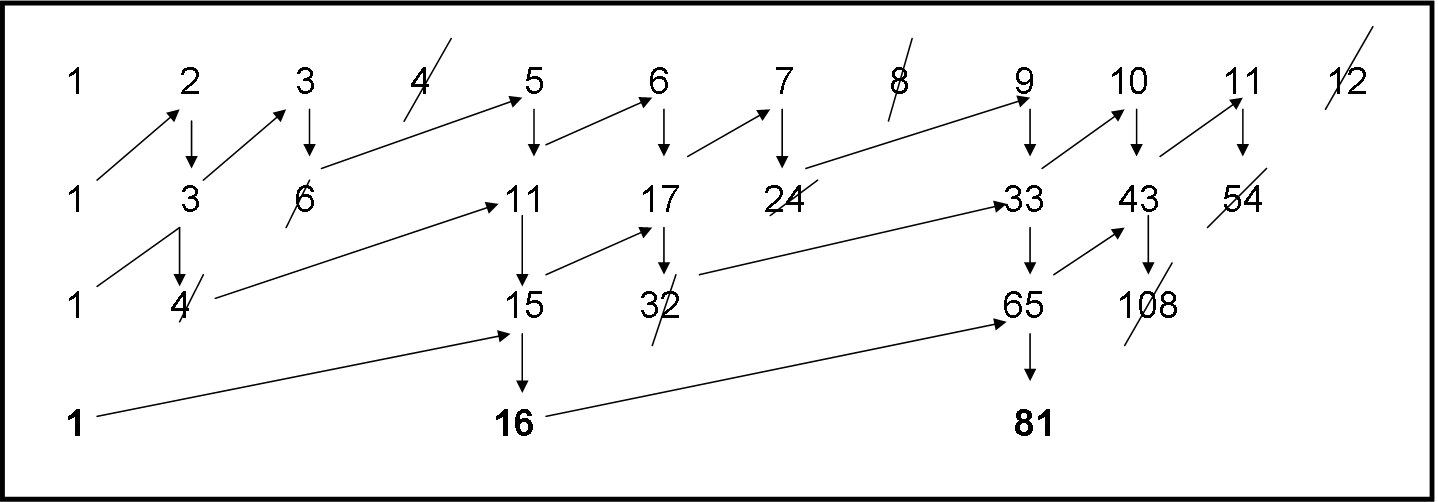
Partiamo sempre dalla solita serie completa, però, eliminiamo il quarto numero (tre salvati e uno cancellato). A questo punto facciamo la ben nota operazione e costruiamo la seconda linea, composta da: 1, 3, 6, 11, 12 , 19, 27, 48, … Un mondo del tutto astruso e conosciuto. Non ci curiamo di lui e proseguiamo: eliminiamo un numero ogni 2 e otteniamo la serie della terza riga: 1, 4, 15, 65, 108, …. Ancora un passo e da questa riga eliminiamo un numero sì e uno no. Si ottiene, infine, la quarta riga: 1, 16, 81, …

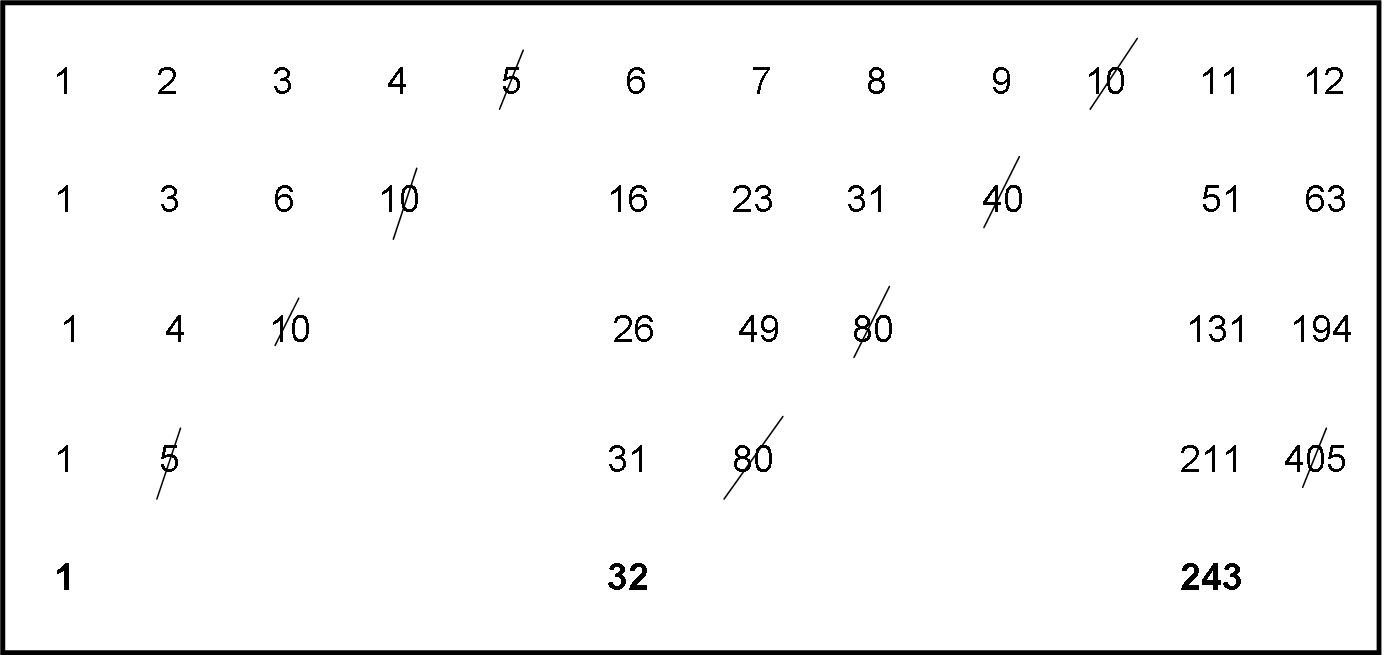
Non ne avreste più bisogno, dato che penso abbiate capito dove si arriva proseguendo nel “gioco”. Comunque, in Fig. 10 ricominciamo da capo e cancelliamo il quinto numero. Si costruisce una nuova riga, dove si elimina il quarto numero; un’altra riga e eliminiamo il terzo numero; un’altra riga e eliminiamo il secondo numero. Costruiamo, infine, l’ultima riga e si ottiene la serie: 1, 32, 243, ...

Ricapitoliamo:

Eliminando il secondo numero otteniamo: 1, 4, 9, 16, 25, …   =  1², 2², 3², 4², 5²

Eliminando il terzo numero otteniamo: 1, 8, 27, 64, …  =  1³, 2³, 3³, 4³

Eliminando il quarto numero otteniamo: 1, 16, 81, …   =  1⁴, 2⁴, 3⁴

Eliminando il quinto numero otteniamo: 1, 32, 243, …  =  1⁵, 2⁵, 3⁵

In realtà, possiamo anche aggiungere, all’inizio, la serie di tutti i numeri (senza eliminarne nessuno).

Ricordandoci che ogni numero può essere rappresentato da un mucchio di sassolini, non è difficile costruire la Fig. 11 che ci porta dritti dritti verso un altro tipo di Universi paralleli.

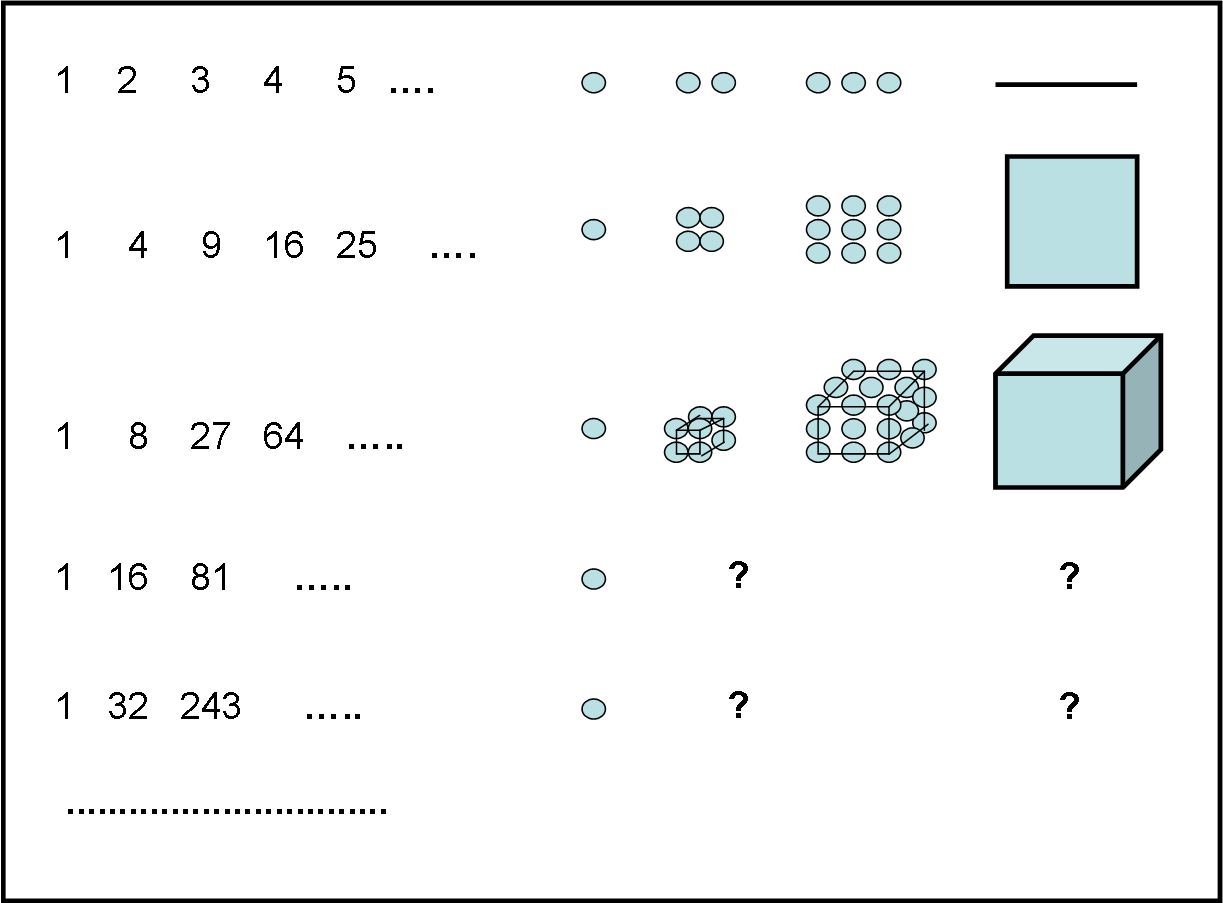
Il primo è quello LINEARE, a UNA DIMENSIONE

Infatti ogni numero può essere rappresentato con un sassolino, due sassolini, tre sassolini, posti uno a fianco dell’altro. In pratica disegniamo dei segmenti.

Il secondo è l’Universo QUADRATO, A DUE DIMENSIONI

Infatti, ogni numero può essere disegnato con un quadrato che ha 1, 2, 3, 4 sassolini come lati

Il terzo è l’Universo CUBICO, a TRE DIMENSIONI

Infatti ogni numero (chiamiamolo attore) può essere rappresentato come un cubo che ha 1, 2, 3, 4, … sassolini come spigoli

Il quarto è l’Universo a QUATTRO DIMENSIONI… ma come possiamo rappresentarlo attraverso i sassolini? Purtroppo noi non siamo in grado di farlo. Siamo ancora troppo primitivi. I numeri ci superano senza problemi…

E pensare che il gioco può andare avanti fino a qualsiasi dimensione n-esima, ma noi non sapremmo cosa fare dei nostri sassolini. Eppure questi numeri esistono sicuramente e riusciamo, con molta limitatezza, a scriverli con delle cifre. Ma la loro vera essenza e quella dei rispettivi Universi ci è vietata!

Non ci sarà passato inosservato il fatto che certi “numeri” (ma parliamone con molto rispetto) appartengono a Universi di dimensioni diverse. Ad esempio, il 16 appartiene a quello a due e a quattro dimensioni. Un punto di passaggio tra Universi diversi? I numeri ce lo stanno indicando, ma noi siamo ancora troppo limitati per seguire le loro indicazioni… Certi numeri hanno stati diversi nello stesso Universo a due dimensioni (possono essere poligoni diversi), ma altri rappresentano stati diversi in Universi a dimensioni diverse (possono essere quadrati – a due dimensioni-  ma anche “attori” a quattro dimensioni).

La cosa più importante è, comunque, che noi non siamo capaci di costruire numeri con dimensioni maggiori di tre. Siamo o non siamo ben piccola cosa rispetto a loro?

Pensate, poi, che nell’Universo a tre dimensioni potremmo benissimo costruire piramidi, esaedri e quello che volete… Infiniti Universi all’interno di ogni Universo a n dimensioni. E che dire poi se ripetessimo la nostra operazione delle righe sovrapposte a serie di numeri già selezionati (triangolari ad esempio?). E se sommassimo in qualche strano modo interi Universi n-dimensionali…?

La testa ci sta girando… altro che stringhe, brane, multiversi a 6 o 7 dimensioni, materie brillanti o oscure…

In ogni modo, per restare con i piedi per terra, attraverso la costruzione che ci ha permesso di costruire infiniti Universi numerici -teorema di Moessner-  siamo in grado di calcolare tutte le potenze dei numeri naturali facendo delle semplici somme…

Va bene, va bene… torniamo ai nostri numeri perfetti (bastano e avanzano)

Numeri perfetti

Abbiamo visto numeri difettivi e numeri eccedenti, ciascuno con i suoi problemi esistenziali. I loro stessi nomi indicano chiaramente che devono esistere anche dei numeri perfetti, ossia tali che la somma dei loro divisori sia esattamente uguale al numero. E si apre un argomento ancora oggi non risolto del tutto…

Sembra che sia stato Pitagora a metterli in evidenza, ma probabilmente esistevano già da secoli, in culture più antiche.

La sua scuola definisce un numero perfetto come un numero naturale (numero intero positivo) che sia uguale alla somma dei suoi divisori, includendo anche il numero uno (ma escludendo il numero stesso).

Il numero 6 ha come divisori 1, 2 e 3. Sommiamoli e troviamo nuovamente 6.

6 = 1 + 2 + 3

Il numero 6 è un numero perfetto! Ed è anche un numero triangolare (tre sassolini in basso, poi due e infine uno in alto). Il numero perfetto che segue è 28, infatti:

28 = 1 + 2 + 4 + 7 + 14

Possiamo notare subito che anche lui è triangolare… In realtà, tutti i numeri perfetti sono triangolari, ma non è vero il viceversa: non tutti i numeri triangolari sono perfetti! Parliamoci chiaro… a questo punto molti di noi hanno già la testa che gira, pur avendo a disposizione non solo matita e foglio, ma anche computer e macchinette calcolatrici. I greci, invece, continuarono a studiare sia per il piacere intrinseco dei numeri e dei loro giochi, sia per il significato ben più generale che a loro veniva dato. Un  numero era perfetto sia “matematicamente” sia “filosoficamente”.

Pitagora, perciò, decise che doveva capire cosa stava dietro alla perfezione dei numeri, ossia come essi si formavano. Egli, forse, aveva grande ammirazione per le donne e per la loro “diversità”, fatto sta che si impuntò sul numero 2 e cominciò a calcolarne tutte le potenze

2² = 4

2³ = 8

2⁴ = 16

2⁵ = 32

2⁶ = 64

E poi verificò se fossero perfetti

4 = 2 + 1 = 3

8 = 4 + 2 + 1 = 7

16 = 8 + 4 + 2 + 1 = 15

32 = 16 + 8 + 4 + 2 + 1 = 31

64 = 32 + 16 + 8 + 4 + 2 + 1 = 63

No, non lo erano; però, erano tutti lievemente difettivi (inferiori di una sola unità).

Inoltre, la somma dei loro divisori è ovviamente formata sempre dalle potenze di 2. In linguaggio moderno potremmo concludere che:

2ⁿ è sempre un numero leggermente difettivo e la somma dei divisori può scriversi come

2⁰ + 2¹ + 2² + 2³ + 2⁴ + 2⁵ + … + 2^n-1

Pitagora non aggiunse altro, probabilmente, e bisognò aspettare Euclide… circa due secoli dopo per un salto in avanti veramente fondamentale.

Tuttavia, Pitagora e la sua scuola riuscirono a trovare, in modo empirico, i primi quattro numeri perfetti: 6, 28, 496, 8128. Si posero due domande non semplici: (1) esiste un  numero perfetto dispari? (2) esistono infiniti numeri perfetti? La risposta non è semplice e le due domande formano quello che è considerato da tanti “il più antico problema matematico”.

Cerchiamo di immedesimarci in quei tempi. I numeri erano qualcosa di magico e sovrannaturale. Elaborarli, trovare le loro misteriose relazioni e gli altrettanto misteriosi significati profondi era una ragione di vita e di vicinanza all’Universo, l’unico in grado di rispondere compiutamente. Una situazione apparentemente primitiva, ma di un’importanza scientifica enorme! Se poi pensiamo ai mezzi a disposizione la faccenda diventa quasi incredibile.

Torniamo a noi e ascoltiamo Euclide.

La somma di una serie geometrica , oggi, sappiamo benissimo a quanto corrisponde. Essa ha come risultato finale:

∑^n-1_{k = 0} x^k = (1 - x^k+1)/(1 – x)

Nel nostro caso x = 2, ossia:

∑^n-1_{k = 0} 2^k = (1 – 2ⁿ)/(1 - 2) = 2ⁿ - 1

Essa è la somma dei divisori di 2ⁿ

Tuttavia, Euclide era costretto a dirlo a parole, nel seguente modo: “A partire dall’unità si sommano tutte le potenze di due fino a trovare un  numero primo”, ossia fermandosi a 2ⁿ -1 numero primo. Ebbene: “ Il prodotto di questa somma per l’ultimo numero della serie è SEMPRE un numero perfetto PARI”. Ossia:

(2ⁿ – 1) 2^{n - 1}       …. (2)

è sempre un numero perfetto pari!

Attenzione, però, non dice che non esistano numeri perfetti che abbiano forma diversa. Dice solo che quelli scritti in quella forma sono sicuramente perfetti!

Euclide non si limita a esporre la sua congettura, ma ne dà una dimostrazione rigorosa, di non facile descrizione, che evitiamo, ma che è segno della grande capacità razionale, malgrado i sassolini restino sassolini…

Tutto risolto? Nemmeno per sogno… per trovare i numeri perfetti si devono trovare i numeri primi che sono dati dalla serie delle potenze di 2. Non solo, ma la formula di Euclide dice che un numero che soddisfa la (2) è perfetto, ma non dice che tutti numeri perfetti possano essere scritti in quel modo.

In particolare dice anche che 2ⁿ – 1 è primo se n è primo, ma non dice che non vi sia un numero n primo a dare, comunque, un numero non primo della forma 2ⁿ – 1. In parole più sintetiche e precise : Affinché il numero 2ⁿ - 1 sia primo è necessario che n sia primo, ma non è sufficiente! Ossia esistono n primi che possono dare numeri finali NON primi.

Proviamo a verificarlo.

Per n = 2 (primo) abbiamo 2² = 4 e quindi 2ⁿ - 1 = 4 – 1 =  3 (primo)   OK

Per n = 3 (primo) abbiamo 2³ = 8 e quindi 2³ – 1 = 8 – 1 = 7 (primo)   OK

Per n = 5 (primo) abbiamo 2⁵ = 32 e quindi 2⁵ – 1 = 32 – 1 = 31 (primo)  OK

Sembrerebbe funzionare sempre, ma con i numeri non bisogna avere fretta… Andiamo avanti fino ad arrivare al numero primo 11 (un numero tanto caro a Valentina):

Per n = 11 (primo) abbiamo 2¹¹ = 2048 e quindi 2¹¹ – 1 = 2047 = 23 ∙ 89  (NON primo).

Un paio di risultati niente male per quei tempi…

Per fare un passetto in più bisogna aspettare Nicomaco di Gerasa che fa alcune congetture, per lo più errate, ma una è invece molto interessante: la formulazione di Euclide definisce tutti i numeri perfetti, ossia tutti i numeri perfetti sono della forma 2^n-1(2ⁿ− 1), per n >1 e  2ⁿ− 1 primo.

Euclide, quindi, avrebbe trovato che non solo i suoi numeri sono perfetti, ma anche che la sua “formula” è l’unica che li può creare.

Nessuna dimostrazione, però, da parte di Nicomaco, che, invece, si lancia in considerazioni filosofiche molto suggestive riguardo ai difetti e agli eccessi dei numeri non perfetti e alle successive implicazioni religiose sui numeri perfetti.

In effetti, 6 è il numero di giorni in cui Dio creò il mondo, e 28 è il numero scelto da Dio come numero di giorni che occorrono alla Luna per girare intorno alla terra. Perfino sant’Agostino ne discute in modo molto drastico: “Sei è un numero perfetto per se stesso, e non perché Dio creò tutte le cose in sei giorni; è vero piuttosto l’inverso: Dio creò tutte le cose in sei giorni perché sei è un numero perfetto. E rimarrebbe perfetto anche se l’opera dei sei giorni non esistesse.

I numeri perfetti continuarono a interessare i matematici di varie culture, pur senza arrivare a formulazioni esatte. Si trovarono, comunque nuovi numeri perfetti.

Un certo Hudalrichus Regius, all’inizio del 1500, riuscì a mostrare che 2¹³ − 1 = 8191 è primo, scoprendo, di conseguenza, il quinto numero perfetto 2¹²(2¹³ − 1) = 33550336. Un bel salto e un chiaro segno che i numeri perfetti sono tutt’altro che comuni!

Il sesto numero perfetto arrivò all’inizio del ‘600, con Cataldi: 2¹⁶(2¹⁷ − 1) = 8589869056, così come il settimo: 2¹⁸(2¹⁹ − 1) = 137438691328.

Un grande contributo fu anche dato da Pierre de Fermat, attraverso alcuni suoi teoremi, ma per adesso non ci soffermiamo su di lui (ne torneremo sicuramente a parlare…), quanto sulle conseguenze dei suoi studi. In particolare quelle portate avanti da Mersenne, un monaco estremamente interessato all’argomento.

Egli preparò con grande fatica una tabella di tutti i numeri del tipo 2ⁿ – 1, che vengono ancora chiamati numeri di Mersenne. Tra di loro indicò i numeri che hanno n primo e che sono anch’essi primi. Li possiamo indicare come:

2^p - 1

Essi prendono il nome di numeri primi di Mersenne. Egli arrivò fino a n = 257, trovando 47 numeri primi e commettendo solo 5 errori.

La faccenda si era fatta molto chiara. Con i  numeri primi di Mersenne era immediato trovare i numeri perfetti con la formula di Euclide.

Eulero conferma Euclide

Il passo decisivo in avanti viene fatto da Eulero, che dimostra che: “Qualsiasi numero perfetto pari deve essere scritto nella forma data da Euclide, con la condizione che n sia primo”, ossia dimostra la congettura di Nicomaco. I numeri di Mersenne (esatti) diventano quindi fondamentali per determinare i numeri perfetti pari, senza rischi di perderne qualcuno per strada. Fu quasi immediato per lui determinare l’ottavo numero perfetto: 2³⁰(2³¹ − 1) = 2305843008139952128.

Eulero dimostra anche che tutti i numeri perfetti pari devono finire per 6 e per 8.

La formula decisiva è quindi:

2^{p -1} (2p – 1)

Essa permette di ricavare tutti i numeri perfetti pari a partire dai numeri di Mersenne.

Eulero cercò anche di risolvere il problema dei numeri perfetti dispari, ma senza successo e senza trovarne nemmeno uno.

Potrebbe sembrare strano, ma il numero perfetto scoperto da Eulero rimase il più grande numero perfetto conosciuto per ben 150 anni e ormai anche i matematici si erano rassegnati, come esprime Peter Barlow nel 1811 a proposito del numero perfetto di Eulero: “ ... E’ il più grande che verrà mai scoperto; anche perché essi stimolano soltanto la curiosità, senza essere utili, ed è improbabile che qualcuno cercherà mai di trovarne uno oltre questo.”

Cosa rivelatasi, poi, non vera e ancora oggi i numeri perfetti sono argomento di studio e di misteri, come quello dei perfetti dispari (esistono oppure no?) e se sono finiti o infiniti.

Al giorno d’oggi si conoscono solo 49 numeri perfetti. L’ultimo calcolato manualmente risale al 1911 e ha 44677235 cifre: 2⁸⁸(2⁸⁹ − 1). Nel 2013 è stato scoperto l'ultimo “più grande” numero primo di Mersenne 2^57885161 − 1 (17 milioni di cifre!). In effetti, con lo sviluppo dei computer c’è stato un rinnovato interesse nello scoprire i numeri primi di Mersenne e di conseguenza i numeri perfetti e le scoperte si sono succedute sempre più frequentemente.

Ricordiamo che i numeri perfetti nascondono molte peculiarità. Ad esempio:

La somma dei reciproci dei divisori di un numero perfetto (incluso il numero stesso) è uguale a 2.

Ogni numero perfetto pari, tranne il 6, è uguale a somme di successioni dei numeri dispari al cubo.

Tutti i numeri perfetti sono sia triangolari che esagonali.

Un piccolo esercizio? Provate a sommare le singole cifre di un numero perfetto fino a raggiungere una sola cifra… Il risultato è molto interessante!

Ovviamente, un premio SPECIALE a chi troverà un numero perfetto dispari!

“Un problema di teoria dei numeri è senza tempo come un'opera d'arte.” (D.Hilbert)

Appendice: il crivello di Eratostene

Sappiamo tutti benissimo che un numero è primo quando non ha altri divisori che se stesso e il numero uno. Questi numeri molto “scontrosi” erano già noti fin dall’antichità più remota, ma fu uno scienziato greco, che ben conosciamo per ragioni astronomiche, a fornire un sistema rapido e geniale per determinarli (almeno fino a numeri non mostruosi). Stiamo parlando di Eratostene di Cirene, quel genio che fu in grado di calcolare la circonferenza della Terra con una precisione sbalorditiva, utilizzando proprio lo gnomone di cui abbiamo parlato “matematicamente” QUI (invece QUI abbiamo parlato proprio con lui!).

Vi chiedo solo di imitarlo e di trovare i numeri primi compresi tra 1 e 120 (il numero 1 non è considerato primo, per cui il primo… primo è 2). Disegnate una tabellina (tipo Tavola Pitagorica) che abbia tutti i numeri da 1 a 120 scritti su 12 righe contenenti ciascuna i numeri da 1 a 10, da 11 a 20, ecc., fino a 120. Fate i vostri ragionamenti e poi cerchiate i numeri primi contenuti nell’esempio numerico.

In poche parole, basta descrivere il “crivello di Eratostene”, una specie di setaccio (crivello, appunto…).

Una volta scritta la tabella composta dalle varie righe dei numeri interi che vanno da 1 a 120, cominciamo dal numero 2 (il numero 1 va escluso dato che non è considerato primo). Iniziamo a usare il setaccio per i multipli di 2, cancellandoli tutti. Essendo suoi multipli non possono certo essere numeri primi (hanno sicuramente come divisore proprio 2). Il 2 viene lasciato dato che lui è primo. Lasciamo anche il 3 (primo), ma eliminiamo tutti multipli di 3. Il numero che segue è 5 (non 4 che è già stato cancellato). 5 è primo e, allora, cancelliamo tutti i suoi multipli. Il 6 è già stato cancellato e passiamo al 7. Via con il setaccio del 7 e dei suoi multipli. Adesso dobbiamo saltare l’8, il 9 e il 10 già cancellati e riferirci al numero 11, che è primo. Non faremo un granché, però, dato che i multipli di 11 sono 22, 33, 44, 55, 66, 77, 88, 99, 110, 121. Fino al 110 erano stati cancellati (divisibili per 2 o per 3 o per 5 o per 7) e  il 121 è fuori dalla nostra tabella…

A questo punto è inutile proseguire… Il numero 13 darebbe multipli sicuramente già calcolati, almeno fino a 120 (13 per 11 è 143 ed è già fuori dalla tabella originaria, mentre gli altri precedenti sono già stati cancellati in quanto multipli dei numeri primi già considerati). In altre parole, se il quadrato del numero supera 120 è inutile proseguire.

Ci accorgiamo che non sono passati al setaccio i numeri seguenti:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113

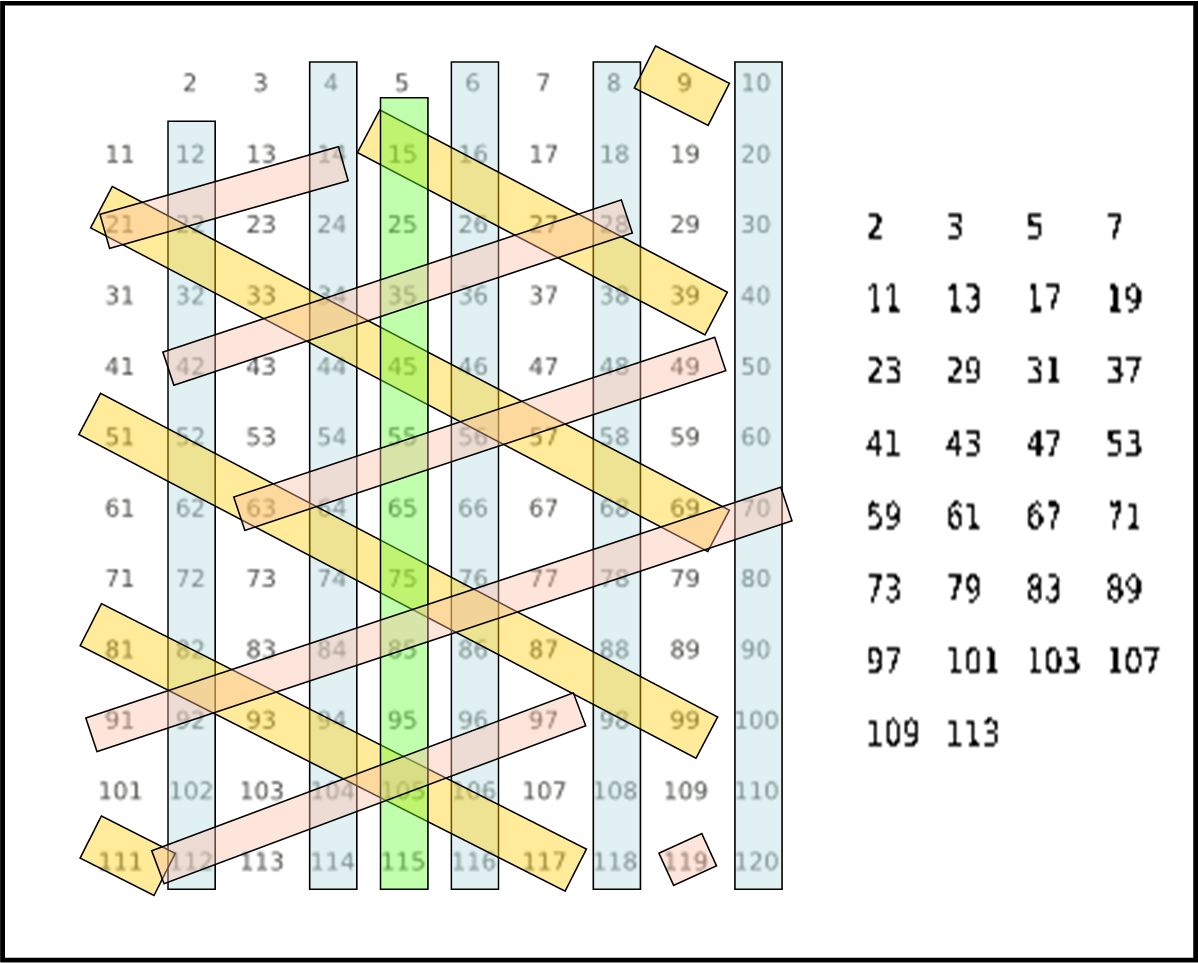
Vediamolo anche attraverso la tabella riportata di seguito:

Non è stato certo difficile eliminare i multipli dei primi numeri primi. Ricordiamo, infatti, che i multipli di 2 devono essere tutti pari e quindi si possono eliminare facilmente con le colonne azzurre. Intanto, notiamo, che qualsiasi numero primo deve essere dispari, tranne proprio il 2. I multipli di 3 si riconoscono facilmente dato che la somma delle cifre deve essere  3 oppure 6 oppure 9. Si trovano facilmente con le linee diagonali arancioni. I multipli di 5 devono finire per 0 o per 5. Quelli che finiscono per 0 li abbiamo già eliminati con i multipli di 2 (numeri pari). Restano solo quelli che finiscono per 5, ossia la colonna verde. I multipli di 7, rimasti ancora “liberi” sono, infine, rintracciabili sia con il calcolo che con le diagonali rosa (divertitevi a trovare come si costruiscono e si ripetono). Dopo di che è inutile andare avanti, dato che i multipli dei numeri primi successivi o sono già stati cancellati o superano il 120…

I numeri... che meraviglia. Non usate solo il PC per fare certi calcoli... torniamo, ogni tanto, alla geniale e utilissima Tabella Pitagorica.