E’ stato bello e interessante lavorare in uno spazio sia piano che curvo, a due o a tre dimensioni. Tuttavia, non possiamo dimenticarci che qualsiasi cosa avvenga nello spazio non può non costringere a cambiare anche il tempo. Potremmo già concludere che, se curvo una cosa, devo curvare anche l’altra. Tuttavia, noi siamo interessati non a curvare separatamente le due “cose”, ma a curvare l’unione delle due, ossia lo spaziotempo.

In poche parole, dobbiamo descrivere il moto spaziotemporale. Ce l’ha, in  fondo, già insegnato benissimo Einstein, con l’aiuto del diagramma di Minkowski. In breve: ce l’ha dimostrato la Relatività Ristretta. Qualcuno troverà banale questo articolo (tutto è già stato detto negli approfondimenti, QUI e QUI), ma non credo faccia male riprendere certi concetti base che ci serviranno nel nuovo contesto.

In particolare cosa ha detto Einstein? Stiamo attenti a muoverci nello spazio e a misurare tranquillamente i tempi che impieghiamo per eseguire certi percorsi. Non tutti vedono la stessa cosa. Questo poteva andare bene per Galileo, ma non per noi! A seconda della velocità con cui ci muoviamo, il tempo è costretto a deformarsi rispetto a un certo sistema di riferimento.

Gli orologi di chi viaggia si vedono rallentare sempre più, a mano a mano che la velocità di chi li trasporta aumenta. Al limite, se si viaggiasse alla velocità della luce, gli orologi apparirebbero fermi. Ovviamente, non per chi viaggia, ma per chi guarda da un altro sistema.

Non vogliamo certo riscrivere la Relatività Ristretta e la trasformazione di Lorentz.  Ci basta, in fondo, una sola figura per riassumere la parte che più ci interessa e vedere come viene misurato il tempo, anzi... lo spaziotempo. Ma, prima, facciamo una piccola chiacchierata, tanto per richiamare alcuni concetti fondamentali. Un richiamo non fa mai male…

Consideriamo un sistema di riferimento considerato fermo, il cui tempo T viene misurato lungo la retta perpendicolare allo spazio monodimensionale (per adesso basta e avanza). Immaginiamo di non muoverci e di venire trascinati solo dal tempo (Fig. 1).

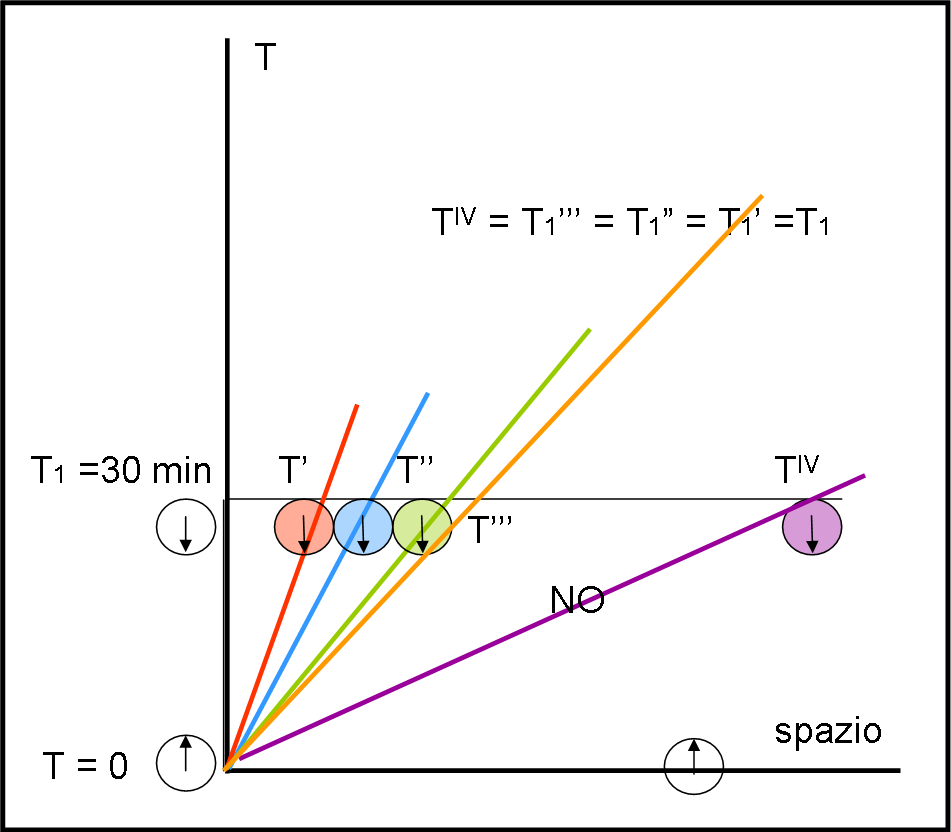
Il nostro orologio (che portiamo in tasca), ma anche i battiti del nostro cuore, scandiscono perfettamente il tempo che passa. Dopo 30 minuti(che possiamo considerare un “tempo unitario”) la nostra lancetta ha ruotato di 180 gradi verso il basso. Chiamiamo questo tempo T₁, considerando T =0 quello all’inizio della misura.

Approfittiamo di questo richiamo, ma lo faremo ancora, per ricordare che TUTTO il sistema di riferimento segue le stesse regole. In particolare, tutti i suoi orologi sono sincronizzati tra loro e indicano lo stesso tempo, come ad esempio l’orologio nero sulla destra. Esso si muove nel tempo, ossia segna lo stesso identico tempo, di quello posto a sinistra.

Fin qui tutto bene. Se il tempo fosse uguale per tutti i sistemi di riferimento (come veniva ipotizzato da Galileo e Newton), vedremmo, all’interno di un’astronave che viaggia a una certa velocità (ossia con una traiettoria indicata dalle linee rettilinee inclinate), un orologio girare esattamente come quelli del sistema di riferimento fermo. Che bello che sarebbe… Ci potremmo muovere nello spazio senza che il tempo ne risenta. Oltretutto, qualsiasi traiettoria sarebbe consentita, ossia qualsiasi velocità. Curvare lo spazio sarebbe più che sufficiente...

A questo punto subentra quello “scocciatore” di Einstein e inizia a dire che la massima velocità ammissibile è quella della luce, ossia del nostro piccolo e instancabile fotone (lui non può mai fermarsi).

Va bene, basta scegliere con cura le coordinate del tempo e dello spazio ed è facile descrivere, nel miglior modo possibile, la traiettoria percorsa dalla luce. Essa è diretta a 45° rispetto all’asse del tempo e dello spazio. Ragione per cui niente può viaggiare con un’inclinazione più bassa rispetto allo spazio. Tutto ciò che si muove nel tempo deve stare tra l’asse del tempo e la retta arancione. La linea viola non può esistere.

Va beh, pazienza… fosse tutto qua il problema. Purtroppo la relatività dice anche altro, ossia obbliga il tempo a scorrere in modo diverso a seconda della velocità a cui si viaggia, sempre che venga osservato da uno stesso sistema di riferimento ipotizzato fermo. Chi viaggia, ovviamente, non si accorge di niente: per lui il proprio orologio va sempre nello stesso modo.

Questo "proprio" orologio segna quello che chiamiamo tempo proprio, uguale per qualsiasi velocità. Una vera e propria distanza spaziotemporale tra due eventi, che non cambia variando il sistema di riferimento, proprio come fa la distanza tra due punti nello spazio galileiano.

Questa costanza, fa sì che l’unità di tempo cambi a seconda della velocità con cui ci si muove, qualora il tutto venga rappresentato nel sistema di riferimento fermo. In altre parole, quando venga usata la rappresentazione spaziotemporale di Minkowski, come riportato in Fig. 2.

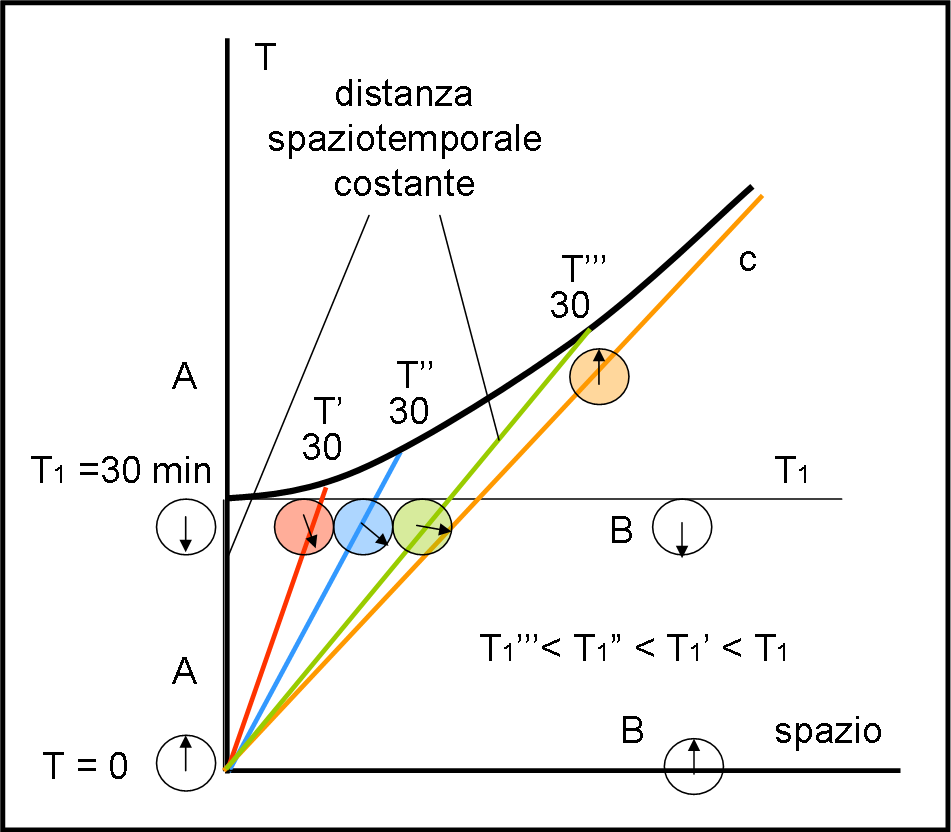
Più si va veloci e più l’unità di tempo si allunga. Addirittura, se si andasse alla velocità della luce, l’unità di tempo avrebbe una lunghezza infinita. Tutte queste parole possono essere sintetizzate da una bellissima curva (iperbole) tracciata in neretto nella figura. Ripetiamo: per chi viaggia il tempo corre sempre nello stesso modo. Per chi sta fermo questa costanza porta a una dilatazione dell’unità di tempo rispetto a quella del proprio orologio.

Ogni linea relativa a una certa velocità (l'asse del tempo) taglia l’iperbole in un punto. La distanza tra questo punto e l’origine degli assi (punto di partenza di ogni sistema) indica l’unità di tempo come viene vista da chi sta fermo. Questa unità non è certo costante se disegnata nello spazio di riferimento fermo, ma lo è, invece, nello spaziotempo e l’iperbole indica la linea di uguale distanza spaziotemporale rispetto alla comune origine.

No, non vi sbagliate di certo, stiamo proprio parlando del celebre invariante dello spaziotempo, una cosa analoga al raggio di una circonferenza in uno spazio piano, come già detto presentando il diagramma di Minkowski.

Cerchiamo di vedere le cose in modo più pratico. Ogni viaggiatore (rosso, blu e verde) ha un suo orologio dello stesso colore. Prima di muoversi segnano tutti zero, come quello di chi sta fermo.

Poi, via… verso nuove avventure, chi più veloce, chi meno! Cosa vede chi sta fermo confrontando i propri orologi perfettamente sincronizzati con quelli dei viaggiatori. Proprio quello che ci aspettavamo… essi girano più lentamente e rallentano sempre di più a mano a mano che la velocità aumenta. Come possiamo accorgerci di ciò, nella figura?

Beh, basta tracciare una linea orizzontale, relativa, ad esempio proprio a 30 minuti di tempo T. Se ci fosse Galileo direbbe che in quel momento tutti gli orologi colorati segnerebbero lo stesso tempo. Adesso, non più. La linea orizzontale, che indica un certo tempo T1 nel sistema fermo, incontra le linee colorate in punti (T1', T1" e T1"'), la cui distanza dall’origine è ben più corta dell’unità relativa alla singola linea, l’unità che scandisce il tempo proprio dell’orologio di chi si muove.

Apparentemente sembrano segmenti più lunghi, ma in realtà sono più corti se facciamo attenzione all’unità di misura di ognuno di loro. D’altra parte il tempo proprio è proprio scandito dalle diverse unità di tempo ed è lui stesso l’invariante relativistico, come si vede bene controllando le intersezioni con l’iperbole in neretto.

Noi, che stiamo fermi, siamo, però, muniti di orologi sincronizzati in qualsiasi punto dello spazio e possiamo fare il confronto tra orologi in moto e orologi del sistema fermo. Dirò adesso una cosa banale, ma che spesso mette in confusione… Non abbiamo bisogno che A abbia un “telescopio” per vedere gli orologi vagabondi, aspettando la loro luce. Se fosse così, introdurremmo un tempo supplementare che adesso non ci serve assolutamente. Basta, innvece, avere una rete di orologi che si trovino al punto giusto, al momento giusto.

Ribadiamo: non c’è assolutamente bisogno di fare un confronto con l’orologio di A, che viaggia lungo l’asse del tempo in modo verticale, a una certa distanza spaziale dal punto d’incontro degli orologi colorati con la linea orizzontale, e che indica il tempo di chi sta fermo. Il confronto si può fare con qualsiasi orologio che appartenga al sistema e che, quindi, giri nello stesso identico modo. La sincronizzazione, all’interno di uno stesso sistema, non viene mai scalfita. Vi è sempre un orologio come quello di B, pronto a fare il confronto. In parole povere, l’astronave attraversala la linea orizzontale in un punto spaziale in cui è sempre presente un orologio che segni T.

Cosa vediamo, attraverso questa rete di orologi? Ci accorgiamo che la lancetta dell’orologio rosso è leggermente più indietro rispetto alla nostra, quella dell’orologio azzurro ancora di più e stessa cosa per quello verde (si è spostato di poco più della metà di quanto non si sia spostato il nostro). Per noi sono passati 30 minuti, ma l’orologio verde segna poco più di 15 minuti. E anche il  cuore dell'astronauta, la sua barba e ogni funzione vitale, è rallentata rispetto alla nostra. Il suo tempo proprio è uguale al nostro (una costante spaziotemporale), ma non ci appare così se viaggia velocissimo rispetto al sistema fermo.

Se guardassimo il fotone vedremmo un orologio (piccolo, piccolo…) che segna sempre e comunque le ore ZERO.

Di quanto rallentano gli orologi colorati? Beh… semplice a calcolarsi! basta fare il confronto tra la lunghezza di traiettoria compiuta e quella necessaria per arrivare all’iperbole, dove scatteranno i 30 minuti per ciascuno di loro. Il fotone raggiungerà l’iperbole solo all’infinito e quindi il suo tempo, per noi, appare sempre lo stesso.

Tutta questa complicazione dello spaziotempo è solo apparente? Assolutamente no, fino a che il viaggiatore si muove. Il suo orologio gira effettivamente più piano rispetto a noi che lo guardiamo. Il caso del muone ne è una prova inconfutabile (QUI). Tuttavia, è anche vero che se considerassimo fermo il sistema verde, ossia che si muove con l’astronave verde, e riferissimo tutto a lui, sarebbe il nostro orologio a subire un rallentamento perfettamente simmetrico. Questa è, in fondo, la base della Relatività Ristretta!

Prima di andare avanti, ribadiamo un concetto semplicissimo che, a volte, può creare confusione. Quando si dice che un orologio rallenta vuol dire che il tempo che misura è più piccolo. In altre parole, l’orologio dell’astronave più veloce è quello che misura il tempo minore.

A questo punto mi potreste dire: “Va bene, un ripasso della Relatività Ristretta fa sempre bene… ma noi vogliamo curvare lo spaziotempo e vogliamo introdurre la relatività generale…”. Calma e sangue freddo. Siamo entrati nello spaziotempo e vogliamo proprio definire le curve in questo nuovo ambiente. Dobbiamo, perciò, definire, prima, cosa si intende per traiettoria rettilinea tra due eventi (non possiamo più parlare di punti, dato che alla posizione abbiamo associato il tempo).

Altro che le già le difficili tre dimensioni del nostro spazio...

Vedremo che la risposta è esattamente il contrario di quanto si asserisce restando nello spazio. Per arrivarci, torniamo al paradosso dei gemelli che è solo un esempio di ciò che capita quando si è liberi di viaggiare nello spaziotempo. Anzi, prepariamoci ad una gara sportiva del futuro…

Riprendiamo la figura precedente e la chiamiamo Fig. 3, con lo stesso sistema di riferimento fermo.

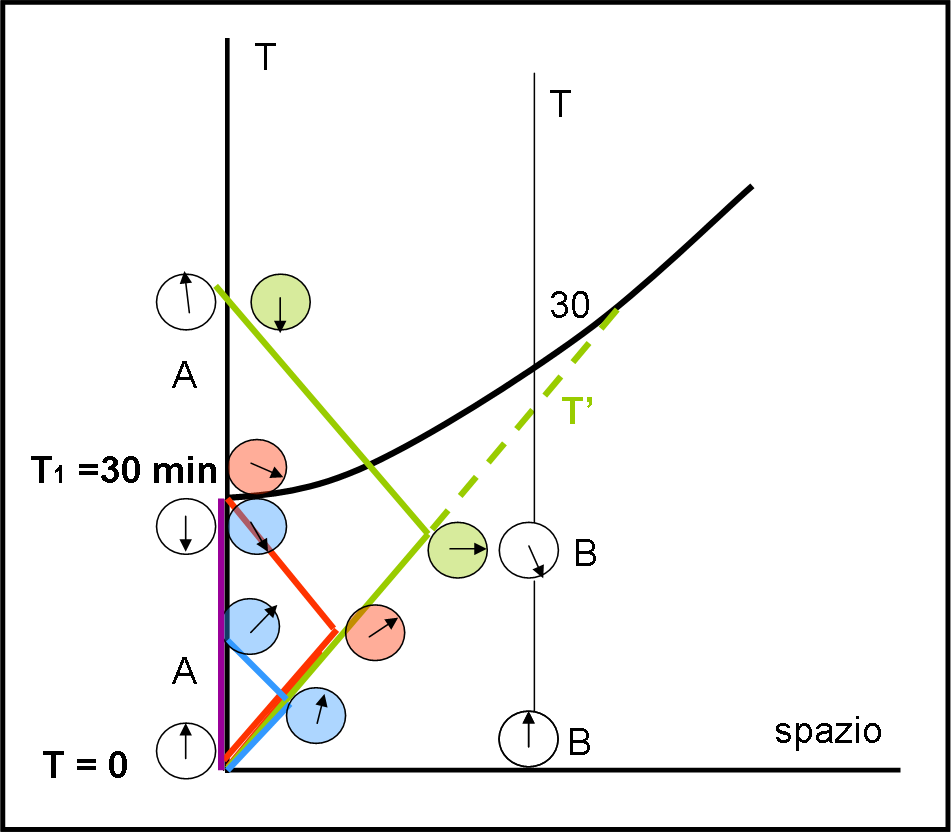
A sia il giudice “assoluto” della gara, che non si muove spazialmente dalla sua posizione di controllo. Intorno a lui ha tanti concorrenti pronti a eseguire l’esercizio che sta per proporre. Ferma, sulla pista dell’astroporto, vi è un’astronave nuova di zecca, che può raggiungere qualsiasi velocità (inferiore a quella della luce, ovviamente). Il compito da svolgere durante la gara è il seguente:

A un dato segnale viene dato il via al concorrente e dopo 30 minuti, misurati con l’orologio di A, sarà dato un secondo segnale. Vincerà la prova chi tornerà al punto di partenza, ossia in A, in tempo per ascoltare il secondo segnale, impiegando, però, secondo il suo orologio, il tempo più lungo possibile. L’ideale sarebbe, perciò, impiegare esattamente 30 minuti e riuscire a sentire il secondo segnale. Questa misura verrà effettuata dal giudice A, sulla base dell’orologio del viaggiatore.

Al limite, vincerà l’astronauta che più si avvicinerà ai 30 minuti. Attenzione: l’astronave impiega un tempo trascurabile per arrivare a una velocità di crociera e lo stesso capita per ogni cambiamento di percorso. Insomma, le accelerazioni e decelerazioni possono essere trascurate nel conteggio del tempo. E’ o non è un’astronave fantastica?!

Lanciato il segnale, parte il primo astronauta verde. Ha al suo servizio un mezzo velocissimo ed è convinto di fare ciò che vuole nello spazio e ritornare sicuramente in tempo per ascoltare il segnale. Deve solo fare attenzione a non tornare troppo tardi. Per essere sicuro decide di trascorrere nello spazio solo 29 minuti per non correre rischi. Il verde parte a una velocità fantastica e si diverte a vedere tutto ciò che lo circonda e non si accorge del sorriso ironico dei giudici “assistenti”, disposti lungo il percorso e che possono direttamente controllare il tempo che sta passando nell’abitacolo.

Il concorrente controlla la situazione, dopo essersi divertito per bene, e valuta che è l’ora di tornare indietro. Frenata quasi repentina e apre la cabina da cui scende felice con il suo orologio in mano. Lui stesso grida 29 minuti e 59 secondi! E attende il suono che indichi la conclusione della gara.

Intorno a lui molti stanno ridendo ed esclamano: “Era ora che arrivassi! E' una vita che è suonata la conclusione”. “Ma come”, dice lui, e mostra al giudice il suo orologio. Il giudice non dice niente e mostra il suo orologio, quello che fa fede per il secondo segnale. Mamma mia… è passato un tempo lunghissimo (non fatemi fare dei calcoli, quello che importa è il concetto). Grida: “Accidenti agli orologi e a chi li ha inventati” e va via con la coda tra le gambe.

Il secondo concorrente (rosso) ha avuto tempo di pensare a lungo, in attesa dell’avversario, e teme che non sia stato l’orologio a non funzionare: per andare sul sicuro e non fare la figura del compagno precedente, viaggia ad alta velocità per molto meno. Poi torna indietro giusto in tempo per sentire il secondo segnale. Il suo orologio purtroppo, segna un tempo decisamente più piccolo dei 30 minuti, ma è convinto che nessuno potrà impiegare più tempo per ascoltare il segnale conclusivo.

Il terzo concorrente (blu), però, malgrado l’estrema prudenza, fa meglio di lui, anche se è costretto a stare parecchio tempo in attesa, vicino al giudice, prima di sentire il segnale e mostrare il proprio orologio. Accidenti, non l’avrebbe mai detto, il suo tempo è decisamente più lungo e si avvicina molto ai 30 minuti.

Il quarto concorrente (viola) ha veramente capito tutto. Sale sull’astronave, ma non accende nemmeno il motore. Aspetta tranquillamente che si senta il segnale e mostra contento il suo orologio: esso segna esattamente 30 minuti. In parole molto banali: il concorrente viola non si è mosso, rispetto al sistema di riferimento dei giudici, e ha impiegato il tempo maggiore.

Sì, lo ammetto, siamo stati estremamente didattici e i più bravi –forse- si saranno annoiati un po’. Tuttavia, per i meno preparati è stato un ottimo esercizio. In entrambi i casi, però siamo arrivati a due conclusioni fondamentali per sapere valutare la curvatura dello spaziotempo.

Analizziamo con calma ciò che è successo, tenendo per noi il fatto indiscutibile che almeno tre dei quattro concorrenti non conoscevano affatto la Relatività Ristretta!

Il concorrente verde si è fidato ciecamente del suo orologio e dopo che erano trascorsi circa 15 minuti ha deciso di tornare indietro. E’ arrivato esattamente in 30 minuti, ma non ha tenuto in conto che il segnale sarebbe stato dato dopo 30 minuti dell’orologio del giudice. Sì, lui ha ottenuto un tempo molto lungo e praticamente uguale a quello massimo, ma non ha potuto sentire il secondo segnale!

Siamo esattamente nel caso del paradosso dei gemelli: il concorrente verde torna a casa veramente più giovane del giudice, ma non ha superato la prova.

Il concorrente rosso, non ha ancora capito bene la faccenda e preferisce tornare a casa molto prima dei 30 minuti del suo orologio e riesce a sentire il secondo segnale. Tuttavia, il suo orologio segna molto meno dei 30 minuti, risultato che gli avrebbe dato la vittoria sicura.

Anche se con meno evidenza si ripete il paradosso dei gemelli: il secondo segnale viene sentito dall’astronauta solo una ventina di minuti dopo la sua partenza.

Il concorrente blu è molto imbarazzato e –pensiamo- abbia voluto, comunque, fare un giro in astronave, senza nemmeno pensare alla gara. Eppure, con sua grande sorpresa impiega nettamente più tempo per sentire il secondo segnale. Ci si avvicina moltissimo.

Il quarto, probabilmente, conosce la Relatività Ristretta o ha fatto tesoro dei risultati dei suoi compagni. Non muovendosi è sicuro di sentire il secondo segnale dopo 30 dei suoi minuti, dato che sono esattamente uguali a quelli del giudice. Avrà sempre tempo per provare l’astronave...

Ammettiamolo… mi sono divertito un po’ a creare diverse situazioni che, comunque, portano sempre a una sola conclusione, che già conoscevamo fin da quando abbiamo discusso il diagramma di Minkowski (QUI). La linea verticale, continua, del tempo è quella in cui si ottiene il massimo tempo di percorrenza, che, in altre parole ci dice che nello spaziotempo un cateto è sempre maggiore dell’ipotenusa. Mentre nello spazio il quadrato di una distanza è dato dalla somma dei quadrati delle due coordinate (x e y), nello spaziotempo il quadrato di un cateto (T)  è uguale alla somma dei quadrati dell’ipotenusa (T’) e dell’altro cateto x. Ossia:

d² = x² + y²

T² = T’² + x²

Una soluzione che già conoscevamo, ma che adesso acquista una grande importanza, se enunciata in modo leggermente diverso. Consideriamo un'astronave che viaggi da A a B (due punti fissi nello spazio). Per raggiungere i due punti potrebbe usare velocità diverse. Potrebbe tentarle tutte (andare prima velocissimo e poi a passo di lumaca o viceversa), ma impiegherebbe sempre più tempo andando a velocità uniforme da A a B. Per capire perfettamente questo concetto, basterebbe cambiare sistema di riferimento e considerare ferma l’astronave (il giudice si muoverebbe con velocità uguale e opposta) e ricadremmo nella “gara” precedente.

Si può perciò dire che nello spaziotempo la linea retta è quella descrivibile con una velocità uniforme e direzione costante, che comporta anche il maggior tempo misurato con l’orologio di chi la percorre

Questa definizione prende il posto di quella analoga utilizzata nello spazio (retta euclidea o retta intrinseca per spazi non euclidei). Quest’ultima, però, definiva anche la curva di minima distanza e di conseguenza la curva percorribile nel minor tempo possibile (chiedetelo ai piloti degli aerei…).

Riassumendo: la curva di minima distanza nello spazio, che è quella che comporta il minimo tempo per essere percorsa, corrisponde nello spaziotempo alla curva percorribile nel tempo più lungo. Esattamente il contrario!

Il moto lungo una linea retta nello spaziotempo è il moto che fa passare da un evento a un altro nel massimo tempo possibile. In altre parole, il moto rettilineo nello spaziotempo è quel moto che fa passare un orologio da un punto, in un certo tempo, a un altro punto, in un altro tempo, in modo tale che la differenza di tempo misurata sull’orologio di bordo sia la massima possibile.

Questa sarà la nostra “retta” di riferimento spaziotemporale, in base alla quale misureremo eventuali curvature.  Attenzione che fino ad adesso abbiamo ragionato SOLO in  termini di relatività ristretta proprio per definire cosa sia la linea intrinsecamente retta. Quando capiterà qualcosa che deformerà lo spaziotempo, ce ne potremo accorgere abbastanza facilmente (si fa per dire).

Anticipiamo un concetto che sarà alla base di molte conseguenze. Nella Relatività Ristretta, se io sto fermo vedo tizio che corre quasi come un fotone. Per il tizio che corre, però, sono io che schizzo a velocità pazzesca. Tutto è perfettamente simmetrico.

Se, invece, inserisco una “stufa” molto strana in un punto dello spazio, la faccenda perde di simmetria. Solo un sistema subisce gli effetti della stufa (ossia della massa), l’altro guarda  soltanto. Il sistema lontano vede la stufa e può calcolarne gli effetti. Chi è vicino alla stufa può ribaltare la situazione? Assolutamente no: la stufa non può trasferirsi da un sistema all’altro. Chi è vicino alla stufa non può dire che rispetto a lui, la stufa si sposta nell’altro sistema di riferimento. La simmetria della Relatività Ristretta non c'è più.

Va beh… ci torneremo presto. Adesso riposiamoci un po’. Devo ancora decidere che strada seguire per arrivare al nocciolo della Relatività Generale (penso che ne userò più di una…).

Abbiamo detto cose già conosciute ai più, ma sono cose sempre abbastanza ostiche concettualmente, e non è male inquadrarle nel contesto che ci interessa...

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI trovate l'approfondimento dedicato alla Relatività Generale