QUIZ: Una torta “virtuale” */**/***/(*****)

18/04/17

QUIZ: Una torta “virtuale” */**/***/(*****)

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:35

Seguendo i consigli di un lettore, la mamma di Pappo e Pippo ha preparato due torte separate, che le sono venute, però differenti: ah, le mamme hanno sempre tante cose da fare… La situazione potrebbe essere drammatica, ma Pippo, come al solito, cerca di complicare le cose e…

Le due torte circolari hanno centri O1 e O2 . Pippo non si accontenta di mangiarsi la più grande, ma vorrebbe mangiarsele tutte e due. Allora, escogita un problema che è sicuro metterà in crisi Pappo e la sua squadretta. Le torte sono di pasta croccante e molto sottili, per cui non è difficile sovrapporle un pochino e ottenere una figura che può essere considerata complanare. La situazione è quella di Fig. 1. (Le due circonferenze possono essere qualsiasi ma NON uguali, così come la loro intersezione deve essere tale che il centro di una non sia contenuta nell’altra).

doppiatorta1

Pippo sfida Pappo con la seguente strana richiesta: “Devi tracciare un diametro in entrambe le torte e segnare i quattro punti in cui i diametri toccano le rispettive circonferenze. Dimmi per quali diametri riesci a costruire una circonferenza (torta virtuale) che passi per questi quattro punti. Ovviamente non hai bisogno di compasso, ti basta una squadretta per dimostrarlo. Se troverai un solo modo per risolvere il problema, ti mangerai la torta più piccola; se ne troverai due, ti mangerai la più grossa; se ne trovi almeno tre, te le mangerai tutte e due! Ricordati che soluzioni simmetriche contano come una soltanto ”.

La situazione di partenza è la Fig. 2 (con due diametri qualsiasi, che ovviamente non corrispondono a quanto richiesto). Il cerchio finale deve passare per A,B,C,D.

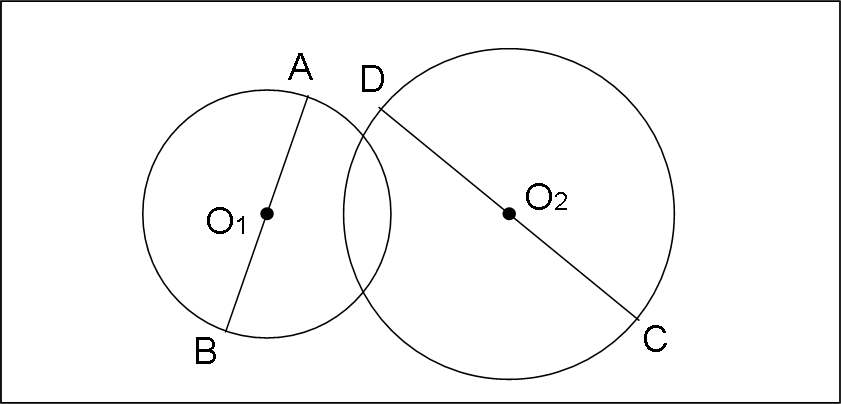
Figura 2
Figura 2

Le soluzioni devono essere trovate e dimostrate per via puramente grafica.

Per i più abili: potrebbero esistere altre soluzioni rispetto alle tre che ho trovato io. Inoltre, penso che sia possibile descrivere in modo analitico le soluzioni riconducendo il tutto a una sola funzione (non ne sono ancora sicuro… mi fido dei più bravi!).

Spero che questo quiz, di impostazione e inizio semplice, possa dar luogo a una fruttuosa discussione con evoluzione sempre più complessa e generale, come è già capitato svariate volte…

Buon divertimento!

 

QUI la prima parte della soluzione

QUI la seconda e ultima parte della soluzione

 

Se vi piacciono i quiz, QUI ne trovate molti e per tutti i gusti!

 

Articoli correlati

35 commenti

  1. Daniela
    18/04/2017 at 09:05

    Hai scritto "Ovviamente non hai bisogno di compasso..."  detto così sembra che il compasso non sia necessario, ma sia consentito: ho capito bene oppure il compasso è vietato?

  2. Arturo Lorenzo
    18/04/2017 at 09:10

    Che bello ricominciare il lavoro sul PC dello studio , dando una preliminare sbirciatina al Circolo...  :-D

    Una soluzione è quando i due diametri AB e CD sono tra loro paralleli. In tal caso, infatti, i punti A, B, C, D risultano essere i vertici di un trapezio isoscele e, essendo il trapezio isoscele sempre inscrivibile in una circonferenza, abbiamo che per tali 4 punti passerà certamente la circonferenza cercata. Che il trapezio isoscele sia sempre inscrivibile in una circonferenza deriva dal fatto che gli assi dei suoi quattro lati passano per uno stesso punto, cioè il centro della circonferenza circoscritta (Un poligono è inscrivibile in una circonferenza se e solo se gli assi relativi ai suoi lati passano tutti per uno stesso punto, e questo punto coincide con il centro della circonferenza circoscritta).

  3. Vincenzo Zappalà
    18/04/2017 at 09:45

    caro Arturo,

    grazie a te il nostro Pappo mangerà almeno la torta più piccola... :-P

    cara Dany,

    direi che è del tutto inutile :roll:

  4. Arturo Lorenzo
    18/04/2017 at 11:48

    Alla mia frase "Una soluzione è quando i due diametri AB e CD sono tra loro paralleli" va aggiunto "e perpendicolari alla congiungente i due centri". Perché quello è il caso particolare a cui facevo riferimento.

    Due domande:

    a) i cerchi sono stabiliti una volta per tutte come quelli della figura 2 o è possibile far variare la misura dei diametri, oltre che la loro angolazione ?

    b) sono considerati accettabili anche il caso in cui A coincide con D e quello in cui B coincide con C ? Se si, questi fornirebbero immediatamente altre due soluzioni possibili, poiché per tre punti (A=D, B, C   oppure A, B=C, D) è sempre possibile far passare una circonferenza.

     

  5. Vincenzo Zappalà
    18/04/2017 at 12:00

    caro Artù,

    le circonferenze e la loro posizione sono stabilite una volta per tutte, ma le considerazioni valgono per qualsiasi altra coppia di circonferenze. Ottima la tua precisazione sulla perpendicolarità...

    b) caso degenere accettato: Pappo si mangia la torta più grande... :) .

    Risolto l'asterisco e i due asterischi, forza con i tre e/o i cinque... :wink:

  6. Arturo Lorenzo
    18/04/2017 at 12:07

    Mi correggo: con riferimento alla domanda B, se accettabili, avremmo una sola soluzione e non due, perché tra loro simmetriche.

  7. Oreste Pautasso
    18/04/2017 at 13:46

    Ci sarebbe anche una cerchio di raggio infinito passante per i quattro punti ABCD allineati lungo la congiungente i due centri quando i due diametri sono entrambi orizzontali...

  8. Vincenzo Zappalà
    18/04/2017 at 14:33

    Beh sì, caro Artù... l'ho già contata come una sola...

  9. Vincenzo Zappalà
    18/04/2017 at 14:35

    Egregio Sig. Pautasso,

    dica a suo cognato Mattia che non dica fregnacce! So benissimo che non è farina del suo sacco... e non valgono nemmeno i cerchi immaginari  :lol:

  10. Arturo Lorenzo
    18/04/2017 at 15:34

    Dunque, poiché un quadrilatero (nel nostro caso ABCD) è inscrivibile in una circonferenza se e solo se due suoi angoli opposti sono supplementari, basterebbe ruotare i due diametri AB e CD in maniera tale che la somma degli angoli in B e in D del quadrilaterio ABCD sia pari a 180°. Poichè , però, non ho un goniometro ma solo una squadretta, cerco il quadrilatero che abbia gli angoli in B e in D retti (verificabili appunto con la squadretta).

    Procedo , dunque, così:

    1. comincio a inclinare il diametro CD, per esempio in senso antiorario, di un certo angolo rispetto alla verticale
    2. con la squadretta traccio la semiretta per D perpendicolare a CD. Se tale semiretta non incontra la circonferenza più piccola, torno al punto 1 e ripeto con una inclinazione diversa
    3. chiamo con A il punto di intersezione tra la semiretta di cui sopra e la circonferenza più piccola
    4. congiungo A con O1 e prolungo tale segmento fino a incontrare la circonferenza piccola in un punto che chiamo B (AB sarà sicuramente, per costruzione, diametro della circonferenza più piccola)
    5. con la squadretta traccio la semiretta per B e perpendicolare ad AB.
    6. se tale semiretta va a finire esattamente in C ho trovato il quadrilatero cercato (vedi figura seguente), altrimenti torno al punto 1 e ripeto il procedimento con una diversa inclinazione.

  11. maurizio bernardi
    18/04/2017 at 18:12

    Per il momento non ho una dimostrazione grafica o analitica, però....

    Se traccio il segmento p1 p2  (collego i punti con massima altezza dei cerchi) e poi lo trasporto parallelamente in modo da individuare i punti C e B, questi assieme ai due punti diametralmente opposti A e D si trovano su una circonferenza.

    Se fosse così (certamente va dimostrato) allora le soluzioni sarebbero infinite.

     

  12. Vincenzo Zappalà
    18/04/2017 at 18:45

    caro Mau...

    dunque... se fosse vero basterebbe tracciare la perpendicolare a CB, nel punto di mezzo. Il centro dovrebbe stare su questa retta, a parità di distanza da C e da B. Ugualmente, però, questo punto dovrebbe avere la stessa distanza da A e D... e qui la vedo male...

    Perché dici, poi, che le soluzioni sarebbero infinite...?

    Sto andando di fretta e potresti anche avere ragione, ma...

  13. maurizio bernardi
    18/04/2017 at 18:52

    Le soluzioni sarebbero infinite perché il segmento parallelo può essere posizionato in un punto a piacere.

    Nel caso che lo posizioni alla sommità dei cerchi ottengo la prima soluzione di Arturo

    Nel caso in cui lo posizioni alla intersezione, ottengo la seconda soluzione.

    In un caso intermedio avrei altre soluzioni (sempre che sia vero...)

    Il sospetto mi è venuto solo perché ho fatto qualche disegno e sembrerebbe funzionare. Ovviamente il ragionamento è tutto da sviluppare.

  14. Vincenzo Zappalà
    18/04/2017 at 18:52

    Mau...

    però potresti tracciare la retta AD, prendere il punto medio e intersecare la retta precedente. Sono uguali le distanze così ottenute? a occhio direi di no...

  15. maurizio bernardi
    18/04/2017 at 19:09

    No, in generale non funziona: ho provato con altri casi e a volte la precisione è molto buona, altre volte  è del tutto sbagliato.

    Tuttavia potrebbe esserci una regola che fornisce almeno una soluzione in un punto preciso. Ci devo pensare.

  16. maurizio bernardi
    19/04/2017 at 00:53

    Detto senza ironia: si può fare solo con la squadretta e Pappo può eseguire ogni operazione.
    La costruzione è corretta e il risultato sembra preciso. Ma perché la retta che passa per P3 (quarto armonico) goda delle proprietà della altre rette (staccare punti che si trovano su una circonferenza) è qualcosa totalmente da capire e spiegare.
    Potrebbe comunque suggerire una dimostrazione/giustificazione puramente geometrica.

    PROCEDIMENTO

    Traccio la congiungente i centri O1 e O2

    Traccio la congiungente P1 Q fino a intersezione in O'.
    (P1 e Q sono i punti della prima soluzione di Arturo)

    Collego P2 con O'
    (P2 è il punto della seconda soluzione, sempre di Arturo)

    Traccio P1 P2 fino a intersezione P4 sulla congiungente i centri. (considerata soluzione non accettabile)

    Esiste una soluzione (P1) nella zona al di sopra dell'intersezione tra i cerchi.
    Una seconda soluzione (P2) nel punto di intersezione.

    Una ulteriore soluzione (P4),degenere in una retta, lungo la congiungente i centri (raggio infinito)

    Cerco la soluzione all'interno dell'area di intersezione.

    dati i tre punti allineati P1 P2 P4 è sempre possibile ricavare un quarto punto in modo da costruire una quaterna armonica.

    Mediante costruzione grafica ricavo il quarto punto del birapporto: P3.

    (traccio inizialmente da P1 una retta che vada a intersecare O'P4 in S e intercetti R sulla O'P2, poi le diagonali del quadrilatero P2 R S P4 che si intersecano in T. Infine traccio la congiungente da O' a T prolungando, oltre P3, fino a individuare i punti D e A sui cerchi dati.)

    Disegno i diametri AB e DC dei due cerchi dati (i diametri richiesti dal quiz)

    I quattro punti BDAC si trovano su una circonferenza il cui centro è O, individuato con la consueta costruzione degli assi dei segmenti (disegnati solo parzialmente).

    OB=OD=OA=OC = 63mm    verificati  nel disegno reale.

    diametro piccolo       50 mm
    diametro grande       80 mm
    distanza tra i centri  50 mm

  17. Vincenzo Zappalà
    19/04/2017 at 05:51

    caro Mau...

    pretendevo molto meno... Pappo non conosce la quaterna armonica... dai, scendi di livello e. trovata la soluzione graficamente "abbastanza" facile, vediamo se possono collegarsi tutte. Forse un modo c'è... :wink:

  18. maurizio bernardi
    19/04/2017 at 15:53

    Provo con questa costruzione....

    Traccio dai punti P' e P" (estremi superiori dei cerchi) le linee passanti per il punto P (intersezione superiore).

    Individuo A su cerchio minore e D sul cerchio maggiore.

    Disegno i due diametri e ottengo rispettivamente B sul cerchio minore e C sul maggiore.

    Collego B e C  con il punto P (linee rosse)

    I triangoli  APB e  DPC sono rettangoli (angolo in P=90)

    Occorre dimostrare che per ACBD passa la circonferenza il cui centro si trova alla intersezione degli assi dei segmenti  AB CB CD  DA.  Può darsi che Arturo abbia qualche idea delle sue...

  19. maurizio bernardi
    19/04/2017 at 15:58

    Rettifico i nomi dei segmenti che sono: AC  CB  BD e  DA  (non disegnati nella figura)

    Il fatto che i triangoli APB e  DPC siano retti in P è ovvio per la costruzione sopra i rispettivi diametri e penso sia irrilevante ai fini della dimostrazione.

     

  20. Vincenzo Zappalà
    19/04/2017 at 16:05

    Oh mamma mia, Mau! per quel tipo di cerchio ci vuole uno squadrone come il Barcellona e non una squadretta da bambini. Prolungare e intersecare rette quasi parallele... forse diminuendo l'intersezione diventa meno gigantesco... prova a rendere il tutto trattabile in un solo foglio... 8-O

  21. Vincenzo Zappalà
    19/04/2017 at 16:22

    Mau... temo che gli assi dei segmenti AD e CB siano praticamente paralleli e non possono incontrarsi dove si incontrano gli assi di BD e CA... così a occhio...

  22. maurizio bernardi
    19/04/2017 at 16:32

    Niente da fare... cambiando le proporzioni dei cerchi è evidente che la precedente costruzione cambia in modo radicale e  non porta a nessun risultato. Lasciare perdere.

  23. Vincenzo Zappalà
    19/04/2017 at 16:50

    Scusi Sig. Maurizio... ma Pappo ha molta fame! Perché non si fa aiutare da quel portentoso amico suo, tale Oreste Pautasso?

  24. maurizio bernardi
    19/04/2017 at 20:06

    Oreste? vogliamo scherzare...?  Guarda cosa mi ha fatto !!

     

    Si è incaponito con questa cosa, che mi ha ..."spiegato" così:

    La linee nere e le lettere nere sono relative alla soluzione 1 (trapezio isoscele). In questa soluzione i due diametri sono paralleli e verticali e il centro del cerchio che passa per ABCD si trova sulla congiungente O1 O2.

    Le linee rosse e le lettere rosse riguardano la soluzione 2 (triangolo con vertice nella intersezione dei cerchi) In questo caso i punti AD sono coincidenti quindi il cerchio passa in realtà per 3 punti e il suo centro è sulla verticale del centro trovato nella precedente soluzione.

    A questo punto viene il bello. Nel punto O blu, intermedio sulla congiungente O nero - O rosso, si trova il centro di un cerchio che passa per ABCD (blu). le posizioni dei due diametri si ottengono unendo O blu a O1 e ad O2 (sono gli assi) e tracciando i diametri  perpendicolarmente ai rispettivi assi.

    Ma non è finita. Riportando  la distanza O nero - O rosso sotto lo stesso O rosso ( in pratica raddoppiano la distanza da O nero) si individua un nuovo centro O verde.  Con lo stesso sistema di prima si congiungono ad esso i centri O1 e O2  (assi) e si tracciano i diametri perpendicolarmente agli assi.

    Non sto a dire le spiegazioni assurde con cui "proiettivamente" ha giustificato questo papocchio.

    Comunque devo dire che le misure dai vari centri ai punti dei rispettivi diametri sembrano molto precise e il fatto che tutti i centri si trovino allineati sulla verticale potrebbe significare qualcosa.

    Caro Enzo, non avrei detto niente se non fosse stato per il tuo suggerimento che ovviamente , Oreste, appena lo ha visto, ha preso al balzo facendomi pressione.  Meno male che Pappo ha già la sua razione grazie ad Arturo. Comunque quel bambino bisogna tenerlo sotto controllo, non vorrei che gli salissero troppo gli zuccheri.

     

     

  25. PapalScherzone
    19/04/2017 at 20:53

    Si può sapere chi doveva tenere d'occhio quel furfante di Pappo?!?  :evil:

    Ormai le torte se l'è già mangiate tutte e due, alla faccia di Pippo, quindi possiamo anche considerare chiuso il quiz!

    :-P

  26. Gianfranco28/08/16
    19/04/2017 at 23:52

    Sembrerebbe che anche con un punto 0 giallo, posto nel segmento o blu - o rosso, si trovano i quattro punti di una circonferenza.

  27. Fabrizio
    20/04/2017 at 01:44

    Non essendo bravo con le costruzioni geometrice, ho provato con un ragionamento analitico.

    Se non ho capito male il problema, credo che esistano infiniti modi per tracciare i due diametri.

    Tracciato un qualsiasi diametro del primo cerchio con un angolo alpha rispetto alla congiungente tra i centri delle due circonferenze, il diametro della seconda circonferenze che permette di tracciare la circonferenza della "torta virtuale" dovrà avere una pendenza beta tale che: \tan(\beta)=-\frac{{{d}^{2}}-{{{{R}_{2}}}^{2}}+{{{{R}_{1}}}^{2}} }{{{d}^{2}}+{{{{R}_{2}}}^{2}}-{{{{R}_{1}}}^{2}}}{\tan(\alpha)}, d è la distanza tra O1 ed O2, R1 ed R2 sono i raggi delle due circonferenze con centro in O1 ed O2.
    Per definire la posizione del centro (O) della "torta virtuale" introduco un sistema di coordinate cartesiane con origine nel punto intermedio tra O1 ed O2 ed asse x diretto come il segmento O1O2. Le coordinate di O saranno:

    x_o=\frac{{{{{R}_{2}}}^{2}}-{{{{R}_{1}}}^{2}}}{2d}, y_o=-\frac{{{d}^{2}}+{{{{R}_{2}}}^{2}}-{{{{R}_{1}}}^{2}}}{2d\,{\tan(\alpha)}}

    x_o non dipende dal diametro scelto, cioè O è sempre sulla perpendicolare all'asse x di coordinata x_o. Al variare dell'angolo alpha la distanza di O dall'asse x varia. O giace sull'asse x per \alpha=90^{o} e si allontana verso il basso per \alpha decrescenti.

    In breve il ragionamento che ho seguito è questo.

    AB e CD sono corde della "torta virtuale" e, rispettivamente, diametri delle circonferenze con centro in O1 ed O2. Per questo, il centro O della "torta virtuale" si deve trovare sia sulla retta perpendicolare ad AB e passante per O1 sia sulla retta perpendicolare a CD passante per O2. La condizione di perpendicolarità ed il passaggio per un punto permette di trovare le equazioni di queste rette. Risolvendo il sistema di queste due equazioni si trovano le coordinate di O ancora come funzione di alpha e beta. Imponendo che  le distanze OA e OC siano uguali, dovono essere raggi di una stessa circonferenza, si trova la relazione tra \tan(\beta) e {\tan(\alpha)}

     

     

     

  28. Vincenzo Zappalà
    20/04/2017 at 06:28

    Dunque... lasciando da parte Scherzy che è solo MOLTO geloso di Pappo...

    a Mau e Orazio direi che non sono ancora convinto che le distanze del nuovo centro dai 4 punti siano uguali tra loro. Secondo me, manca ancora una condizione...

    A Fabrizio dico che se mettesse le lettere nella figura capirei meglio la sua descrizione. Il procedimento sembra corretto, ma mi piacerebbe vedere se comporta veramente quella condizione geometrica che non vedo ancora arrivare graficamente. Oggi purtroppo devo dedicarmi a una traduzione (povero me) e non credo di avere tempo, ma sono convinto che Mau, Gianfranco e Arturo potrebbero verificare quanto detto da Fabry e tradurlo in una condizione geometrica...

    Dai che ormai dovrebbe mancare poco alla "mia" soluzione, che potrebbe essere compresa benissimo nella trattazione generale di Fabry... Hai provato a vedere se le soluzioni precedenti sono verificate?

  29. Vincenzo Zappalà
    20/04/2017 at 06:43

    Aggiungo che la soluzione di Fabry (anche se non va bene per Pappo  :mrgreen: ) sembra piuttosto corretta (sempre che io l'abbia compresa bene  così di fretta...). Lui non fa altro che imporre che il punto finale sia equidistante da quattro punti legati a due a due dall'appartenenza ai due diametri. Il primo passo è quasi ovvio: tracciare le perpendicolari dai centri dei due cerchi originali a due diametri qualsiasi variabili. Poi essi devono essere bloccati dall'ulteriore condizione di uguaglianza... Questa condizione potrebbe tradursi nella costruzione geometrica necessaria a Pappo.

  30. Vincenzo Zappalà
    20/04/2017 at 08:10

    NOTA BENE:

    Direi che configurazione generale è stata piuttosto ben evidenziata. Ciò che ancora manca è la condizione aggiuntiva. Resta il fatto che le soluzioni stanno tutte su un'unica retta e quindi penso che Fabrizio possa dare facilmente la soluzione finale analitica. Per aiutare meglio la comprensione di  tutti, reputo sia meglio dare la soluzione grafica che manca e sulla base di questa cercare quella analitica. Troppi commenti complicano la situazione...

    Scrivo e pubblico e poi scatenatevi sul nuovo articolo...

  31. Fabrizio
    20/04/2017 at 14:09

    Dettaglio il procedimento utilizzato aggiungendo la figura richiesta da Enzo.

    Utilizzo un sistema di coordinate cartesiane con centro equidistante da O1 ed O2 ed asse x nella direzione O1O2.

    Le coordinate dei due centri sono O_1\equiv (-\frac{d}{2},0)\; \; O_2\equiv (\frac{d}{2},0).

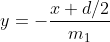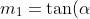    L'equazione della retta passante per O1 e perpendicolare ad AB è: y=-\frac{x+d/2}{m_1}, con m_1=\tan(\alpha)

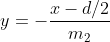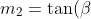    L'equazione della retta passante per O2 e perpendicolare ad CD è: y=-\frac{x-d/2}{m_2}, con m_2=\tan(\beta)

    Il centro della torta deve essere all'intersezione di queste due rette. Le sue coordinate sono la soluzione del sistema composto dalle due equazioni delle rette.

    O\equiv \left ({{x}_{o}}=\frac{d\,\left( {{m}_{2}}+{{m}_{1}}\right) }{2\left( {{m}_{1}}-{{m}_{2}}\right) },{{y}_{o}}=-\frac{d}{{{m}_{1}}-{{m}_{2}}} \right )

    Le coordinate dei punti A e C sono (applico le formule che legano il seno ed il coseno di un angolo alla sua tangente)

    A\equiv \left ({{x}_{a}}=-\frac{{{R}_{1}}}{\sqrt{{{{{m}_{1}}}^{2}}+1}}-\frac{d}{2},{{y}_{a}}=-\frac{{{R}_{1}}{{m}_{1}}}{\sqrt{{{{{m}_{1}}}^{2}}+1}} \right )

    C\equiv \left ({{x}_{c}}=\frac{d}{2}+\frac{{{R}_{2}}}{\sqrt{{{{{m}_{2}}}^{2}}+1}},{{y}_{c}}=\frac{{{R}_{2}}{{m}_{2}}}{\sqrt{{{{{m}_{2}}}^{2}}+1}} \right )

    Le distanze OA e OC devono essere uguali dovendo essere raggi di una stessa circonferenza.

    \bar{OA}^2={{\left( -\frac{d}{{{m}_{2}}-{{m}_{1}}}-\frac{{{R}_{1}}{{m}_{1}}}{\sqrt{{{{{m}_{1}}}^{2}}+1}}\right) }^{2}}+{{\left( \frac{d\,\left( {{m}_{2}}+{{m}_{1}}\right) }{2\left( {{m}_{2}}-{{m}_{1}}\right) }-\frac{{{R}_{1}}}{\sqrt{{{{{m}_{1}}}^{2}}+1}}-\frac{d}{2}\right) }^{2}}

    \bar{OC}^2={{\left( \frac{{{R}_{2}}{{m}_{2}}}{\sqrt{{{{{m}_{2}}}^{2}}+1}}-\frac{d}{{{m}_{2}}-{{m}_{1}}}\right) }^{2}}+{{\left( \frac{{{R}_{2}}}{\sqrt{{{{{m}_{2}}}^{2}}+1}}+\frac{d\,\left( {{m}_{2}}+{{m}_{1}}\right) }{2\left( {{m}_{2}}-{{m}_{1}}\right) }+\frac{d}{2}\right) }^{2}}

    Sviluppando l'uguaglianza tra questi due termini si ottiene

    {{m}_{2}}=-\frac{{{d}^{2}}-{{{{R}_{2}}}^{2}}+{{{{R}_{1}}}^{2}}}{{{d}^{2}}+{{{{R}_{2}}}^{2}}-{{{{R}_{1}}}^{2}}}{{m}_{1}}  cioè {\tan(\beta)}=-\frac{{{d}^{2}}-{{{{R}_{2}}}^{2}}+{{{{R}_{1}}}^{2}}}{{{d}^{2}}+{{{{R}_{2}}}^{2}}-{{{{R}_{1}}}^{2}}}{\tan(\alpha)}

     

  32. Fabrizio
    20/04/2017 at 14:54

    L'allineamento dei centri delle "torte Virtuali" su una retta perpendicolare ad O1O2 credo si possa dimostrare anche applicando il solo teorema di Pitagora. Se la lunghezza q del segmento O1N non dipende dal particolare segmento AB allorra tutti i centri O sono allineati.

    \begin{align*} R^2 &= R_1^2+j^2=R_1^2+(q^2+n^2)\\ R^2 &= R_2^2+l^2=R_2^2+((d-q)^2+n^2) \\ R_1^2&+q^2+n^2= R_2^2+d^2+q^2-2dq+n^2\\ q&=\frac{d^2+R_2^2-R_1^2}{2d} \end{align*}

    Così escono in modo più geometrico le somme e differenze di quadrati.

  33. Vincenzo Zappalà
    20/04/2017 at 15:59

    scusa Fabrizio... può darsi che non abbia capito bene, ma il fatto che AC sia uguale ad AB andrebbe dimostrato non imposto per vedere se il centro sta sulla stessa retta ...

    Resta il fatto che l'equazione finale, che è quella di Arturo, dona  l'equazione della retta perpendicolare.

    Comunque ci sto lavorando anch'io... per adesso ho trovato che i due casi generi stanno sulla stessa retta, adesso provo a vedere se anche il caso qualsiasi concorda...

    Poi tiriamo le somme... :wink:

  34. Vincenzo Zappalà
    20/04/2017 at 16:35

    caro Fabrizio,

    scrivo ancora qui, ma poi è meglio andare nell'altro articolo dove c'è la mia soluzione particolare.

    Penso che arriviamo alla stessa soluzione, dato che i due diametri non sono del tutto casuali, ma dato il primo il secondo deve essere vincolato dal fatto che gli assi dei due diametri si intersechino proprio in un punto della retta verticale dei centri. In altre parole, i due angoli devono essere legati da una relazione come trovi tu...

    Cerco di provarlo geometricamente... e pi ti do conferma.

  35. Fabrizio
    21/04/2017 at 02:47

    Quello che indendevo dimostrare è che tutti i centri delle circonferenze "torte virtuali" sono allineati su una retta perpendicolare all'asse O1O2.  Per questo parto da una qualsisi di queste circonferenze dove OA=OC e da questa assunzione dimostro che il punto N, proiezione perpendicolare di O sull'asse O1O2, si trova in una posizione che non dipende dalla circonferenza scelta quindi è uguale per tutte le "torte virtuali".

    A questo punto la costruzione di una qualsiasi coppia di diametri AB CD diventerebbe quasi banale.

    Prima determino la posizione di N. Probabilmente  il modo più semplice è quello del trapezio isoscele con i due diametri paralleli e perpendicolari all'asse O1O2.

    Trovato N traccio la linea perpendicolare ad O1O2 passante per N.

    Traccio un qualsiasi diametro AB e traccio la linea perpendicolare ad AB passante per O1.

    L'intersezione di questa linea con la linea passante per N determina O.

    Congiungo O con O2 e traccio la sua perpendicolare passante per O2. Le intersezioni di quest'ultima linea con la circoferenza con centro O2 sono i punti CD che definiscono il secondo diametro.

     

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.