Categorie: Matematica
Tags: doppia torta Pappo Pippo quiz soluzione
Scritto da: Vincenzo Zappalà
Commenti:14
Soluzione del quiz sulla torta “virtuale” (prima parte) ***
Arturo ha trovato le prime due soluzioni di questo quiz, mentre sulla terza si è scritto molto e diventa difficile raccapezzarsi con i soli commenti. Preferisco dare la soluzione e continuare con una visione più generale analitica (o anche solo grafica). Ne vedremo ancora delle belle…
Partiamo subito con la soluzione mancante (grafica).
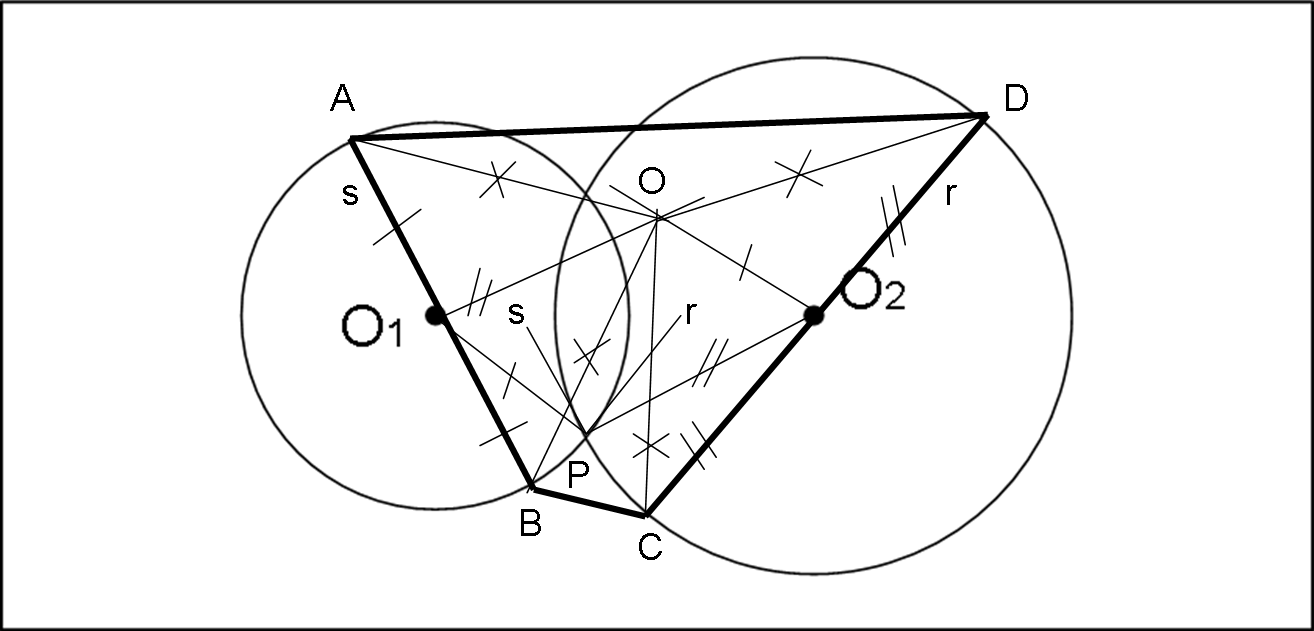Il primo passo da fare è tracciare i raggi O1P e O2P, dove P è uno dei due punti intersezione tra le due circonferenze. Basta adesso tracciare da P le due perpendicolari r e s a questi raggi (che altro non sono che le tangenti in P alle due circonferenze). Consideriamo come diametri delle due circonferenze, i diametri PARALLELI a queste due perpendicolari, ossia AB e CD. Per O1 si traccia la parallela a s e per O2 la parallela a r.
Tracciamo ora gli assi dei due diametri (che partono da O1 e O2). Essi si incontrano in O che è il centro della circonferenza cercata che passa per ABCD.
Bisogna dimostrare che OA= OB = OC = OD.
OA = OB per costruzione (ogni punto dell’asse è equidistante dai due estremi del diametro)
OD = OC per costruzione (come prima)
Tracciamo O1O e O2O.
Il quadrilatero O1PO2O è un parallelogramma per costruzione. Infatti O1P è parallelo a O2O, mentre O2P è parallelo a O1O. Ne segue che i lati opposti devono essere uguali, ossia:
OO2 = O1P
OO1 = O2P
Consideriamo i triangoli AO1O e OO2D. Essi sono rettangoli e uguali, in quanto:
O2D = O2P = O1O
O1A = O1P = OO2
Ne segue che:
AO = DO
E, di conseguenza:
AO = DO = OB = OC
C.V.D.
Le altre due soluzioni limite, già trattate da Arturo (le trovate nei commenti al quiz), hanno il centro della circonferenza sulla stessa retta passante per O e perpendicolare a O1O2.
Ora dovrebbe essere facile trovare una relazione analitica che dia le tre soluzioni e forse anche puramente grafica (magari con un compasso…).
QUI la seconda e ultima parte della soluzione
14 commenti
Secondo me, però, Scherzy, nella discussione sul quiz non stava scherzando quando ha scritto che Pappo ormai si è pappato entrambe le torte
Infatti, nel mio terzo commento avevo indicato una terza soluzione, anche essa particolare di quella generale poi emersa nei commenti di Maurizio e Fabrizio. Cioè, il centro della torta virtuale giace sempre su una retta perpendicolare alla congiungente O1 e O2 e di equazione x=k con k che non dipende dalla inclinazione dei due diametri ma solo dalle ascisse dei due centri e dalla misura dei due diametri. La mia terza soluzione teneva conto, forse per una mia errata interpretazione della richiesta del quiz, della disponibilità della sola squadretta. Quindi considerava solo angoli retti in B e D. Ma in effetti le soluzioni sono infinite. Purtroppo, non posso ora trattenermi oltre qui al PC, il lavoro chiama (anzi urla...) . Vi seguo appena posso , sempre con grande entusiasmo 
E io a quello mi riferivo, perdindirindina, altro che gelosia per Pappo!!
Tu sì che mi comprendi, caro Arturo, mica come qualcun altro...
Non sono pienamente d'accordo... le soluzioni non appaiono infinite, date le due circonferenze di base. Inoltre, la costruzione usata adesso abbisogna solo di una squadretta... Non tutti i punti dell'asse perpendicolare sono centri di circonferenze accettabili. Anzi, temo ce ne sia una sola...
Scusate la forma irrituale, ma ho scritto questa dimostrazione in metropolitane (dettata da Pautasso)...
Se non è abbastanza chiara la potrò illustrare meglio più tardi da casa.
Se non ci sono errori di logica o di calcolo sembra che le soluzioni siano infinite. Trovata una, che ci dice dove è collocata la retta verticale per K , trovo anche le altre.
scusami con la metropolitana... ma quale sarebbe il poligono da iscrivere nel cerchio?
Prolungo BO1 e ottengo A sul cerchio piccolo
Prolungò CO2 e ho D sul cerchio grande
Poligono ABCD.
OB = OA triangolo isoscele
OC = OD. Idem
Ma nella figura che segue, fatto con le stesse modalità non torna...
velocemente, tra fine lavoro in loco e inizio trasferta per lavoro altrove
l'equazione del luogo geometrico dei centri di tutte le torte virtuali è, se faccio coincidere l'origine degli assi con il centro O1:
Ho trovato tale equazione considerando il caso particolare con i due raggi tra loro paralleli e perpendicolari alla congiungente i due centri O1 e O2. Ruotando come si vuole i due raggi AB e CD in modo tale che i punti A, B, C, D stiano tutti su una stessa circonferenza, il centro di tale circonferenza virtuale non si schioda dalla suddetta retta , perpendicolare alla congiungente O1O2. Cambia naturalmente l'ordinata del centro O ma la sua ascissa resta costante e pari a quella di cui sopra.
Enzo... mi sembra che la dimostrazione si applichi anche alla tua figura. Ho aggiunto qualche costruzione e qualche lettera cercando di spiegarmi meglio. Non ho usato Latex perché sono un po' di fretta, ma penso si capisca ugualmente.
Cominciando dalla parte alta della figura ....
Il punto M è il punto medio tra P1 e P2
L'asse di P1 P2 individua K sulla congiungente O1 O2
La verticale passante per K è quella su cui sceglieremo i punti O.
Il punto H , proiezione di M, è il punto medio tra O1 e O2
I triangoli P1P2'P2 e MHK sono rettangoli e simili tra loro. P2P2'/P1P2' = HK/MH (1)
posto che..
d= P1P2' = O1O2 (distanza tra i centri)
HO1=HO2 = d/2
P2P2' = R-r (differenza raggi)
HM = (R+r)/2
HK = e
riscrivo la (1) (R-r)/d = e/((R+r)/2) da cui ricavo: e= (R^2 - r^2)/2d (2)
Le distanze dei centri dall'asse passante per K sono le seguenti:
O1K = s = d/2 + e (3)
O2K = t = d/2 - e
Esprimo ora le distanze di O1 e O2 dal punto O scelto a distanza "x" da K.
OO1 = radq(x^2 + s^2)
OO2 = radq(X^2 + t^2)
Ora veniamo alle distanze OB e OC o addirittura ai loro quadrati.
OB^2 = r^2 + OO1^2
OC^2 = R^2 + OO2^2
sostituendo i valori di OO1 e OO2...
OB^2 = r^2 + x^2 + s^2
OC^2 = R^2 + x^2 + t^2
ora valuto la differenza tra OB^2 e Oc^2
OC^2-OB^2 = R^2 - r^2 + t^2 - s^2
In questa espressione non compare la x, quindi, qualsiasi sia il suo valore si tratta di una costante.
Poiché nella prima soluzione (che ci ha dato K) la differenza è zero, la costante vale zero ed esistono
infinite soluzioni. Proseguiamo in ogni caso con il calcolo.
Sostituendo a "t" e "s" i corrispondenti valori dalle formule (3) :
OC^2 -OB^2 = (R^2-r^2) + (d/2 -e)^2 - (d/2 +e)^2 sviluppando i quadrati e semplificando...
OC^2 - OB^2 = (R^2 - r^2) - 2de ricordando la (2) ...
OC^2 - OB^2 = (R^2 - r^2) - (R^2 - r^2) = 0
Quindi dai calcoli i segmenti OC e OB sembrano uguali.
Dato che i triangoli AOB e COD sono isosceli. anche i segmenti OA e OD avranno la stessa lunghezza.
Così tutti i punti A,B,C,D avranno la medesima distanza da O, centro del cerchio.
caro Mau,
può darsi dipenda solo dalla figura... ma non sembrano proprio uguali OA e OD: OAD non sembra isoscele...
Comunque, mi ci sono messo anch'io (al diavolo la traduzione!) e per adesso ho trovato la soluzione di Arturo (e Fabrizio) per entrambi i casi degeneri. Vado a provare con il caso qualsiasi...
Poi riassumiamo...
Vorrei fare una precisazione iniziale e vedere se siamo tutti d'accordo:
Il procedimento da usare sarebbe il seguente:
SIAMO D'ACCORDO SU QUESTO PUNTO????
Bene... adesso provo a vedere se queste condizioni danno sempre un cerchio che tocchi i quattro punti...
Certo, caro Vincenzo (scusami se mi rifaccio vivo solo ora ma oggi è stata una giornata vissuta di corsa...), le torte virtuali sono infinite elevato alla 1 ... Cioè, non è che si ottengono torte virtuali per qualsiasi coppia di inclinazioni dei due diametri, ma per qualsiasi valore dell'inclinazione di uno dei due. Perché effettivamente si formi la torta virtuale, l'inclinazione dell'altro diametro, una volta fissata quella del primo, è determinata in funzione di quella.
Penso che su questo siamo tutti concordi. E' la premessa alla traccia fissata per la discussione, che impone come vincolo iniziale l'uguaglianza tra i 4 raggi.
L'altro approccio possibile è di fissare il punto O, costruire assi e diametri ed esprimere la distanza da O agli estremi dei diametri.
Senza necessità di calcoli si dimostra immediatamente che la differenza tra queste distanze non dipende da dove ho fissato O, quindi è costante e, avendo almeno due soluzioni per cui la costante vale zero, significa che sarà zero per tutti gli O (infinite soluzioni).
L'espressione delle distanze dei punti A,B,C,D da O ci fornisce il raggio per quel particolare centro O che avevamo fissato.
Mamma mia!!!