Al quiz è stata data una difficoltà variabile perchè poteva essere risolto anche solo intuitivamente. Gli unici due partecipanti , Gianfranco e Paolo, hanno intuito subito il valore dell'angolo a cui corrisponde il valore massimo di larghezza della lastra, ovvero 45°; Paolo si è poi spinto nella direzione giusta, analizzando giustamente (e scomponendo) i movimenti possibili in  quella posizione . La prima parte, quella intuitiva, può essere dimostrata formalmente,  con lo studio dei minimi di una certa funzione.

Schematizziamo quindi la lastra come un segmento nella pianta del corridoio. Essendo la lastra rigida, possiamo pensare di individuare il suo movimento tramite due soli parametri; la lunghezza L e l'angolo che la lastra forma con l' 0rizzontale . La lastra per passare attraverso il corridoio dovrà avere una certa lunghezza , mentre l'angolo dovrà assumere tutti i valori  nell'intervallo   essendo il movimento associabile ad una funzione continua (del tempo) e dovendo passare da una posizione orizzontale a una finale verticale(o viceversa, a seconda del verso di percorrenza). 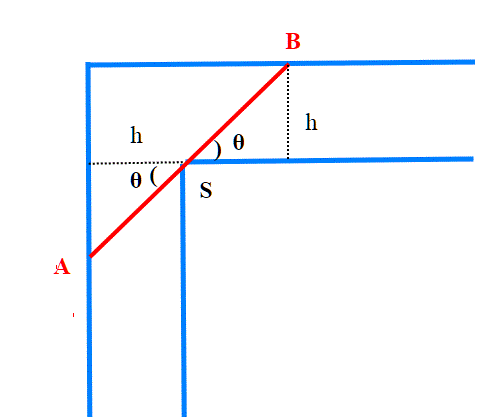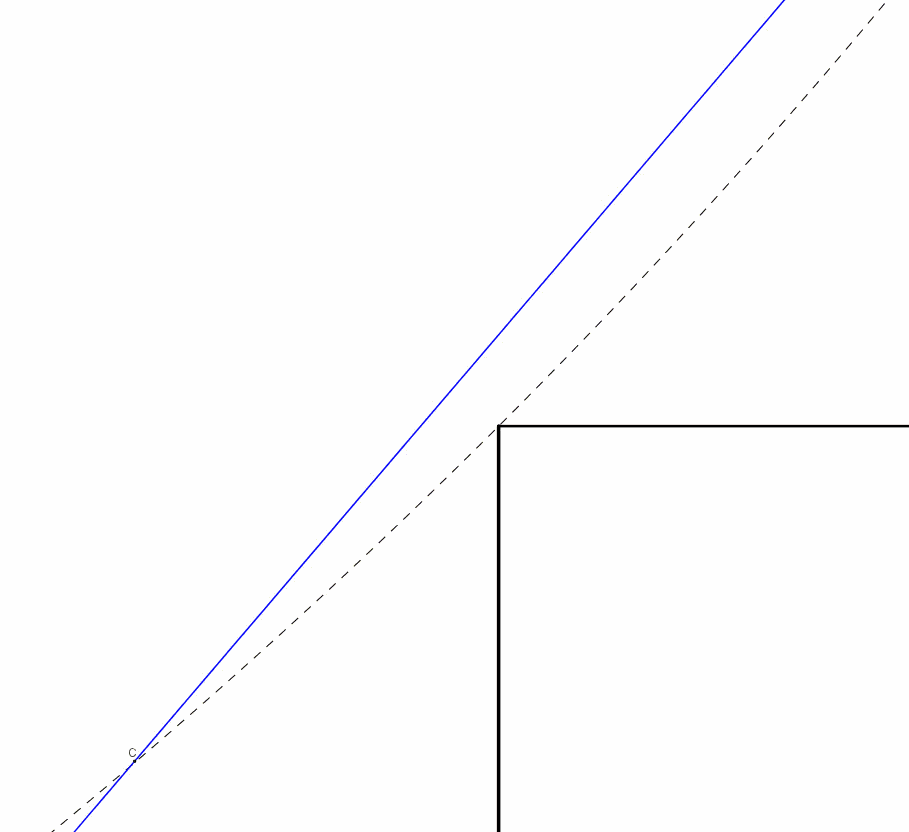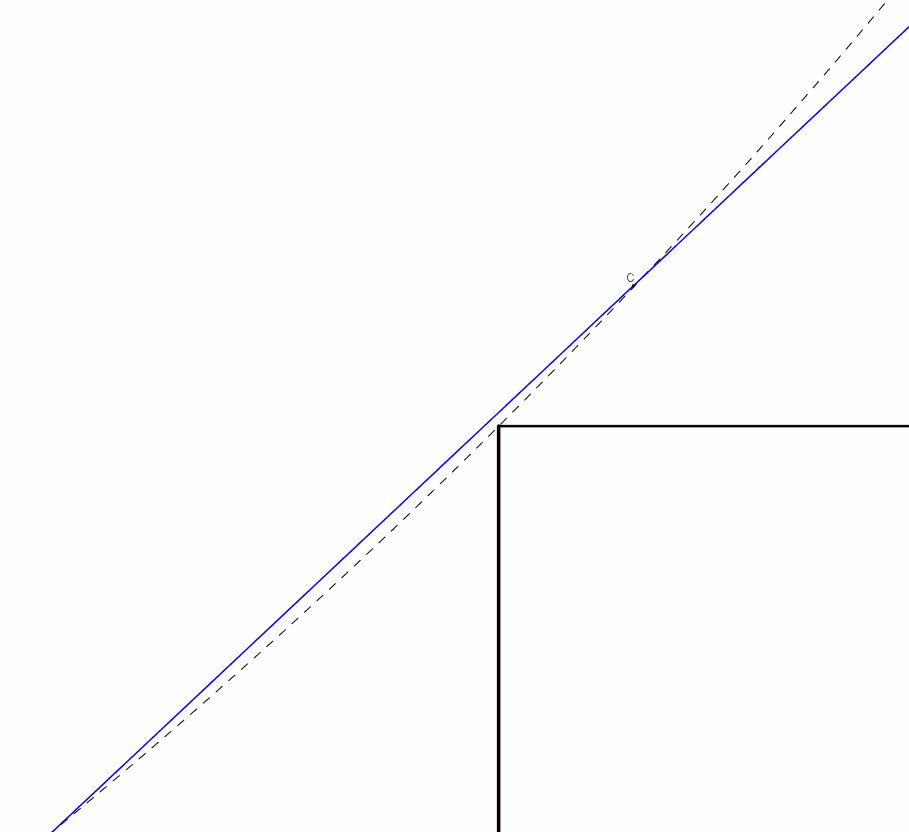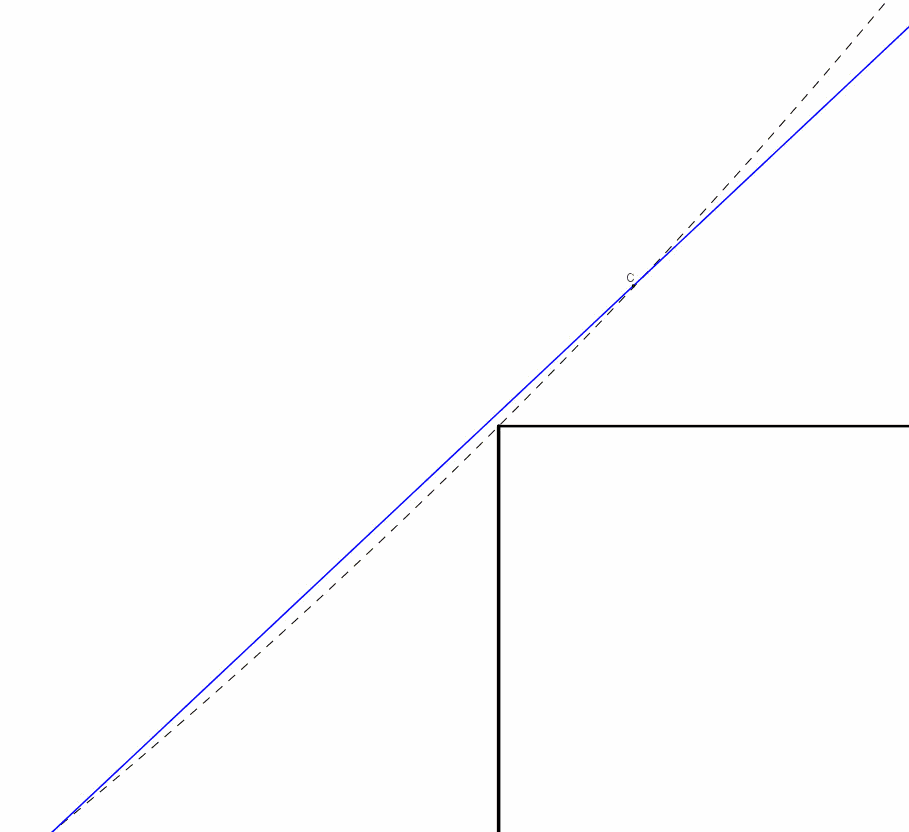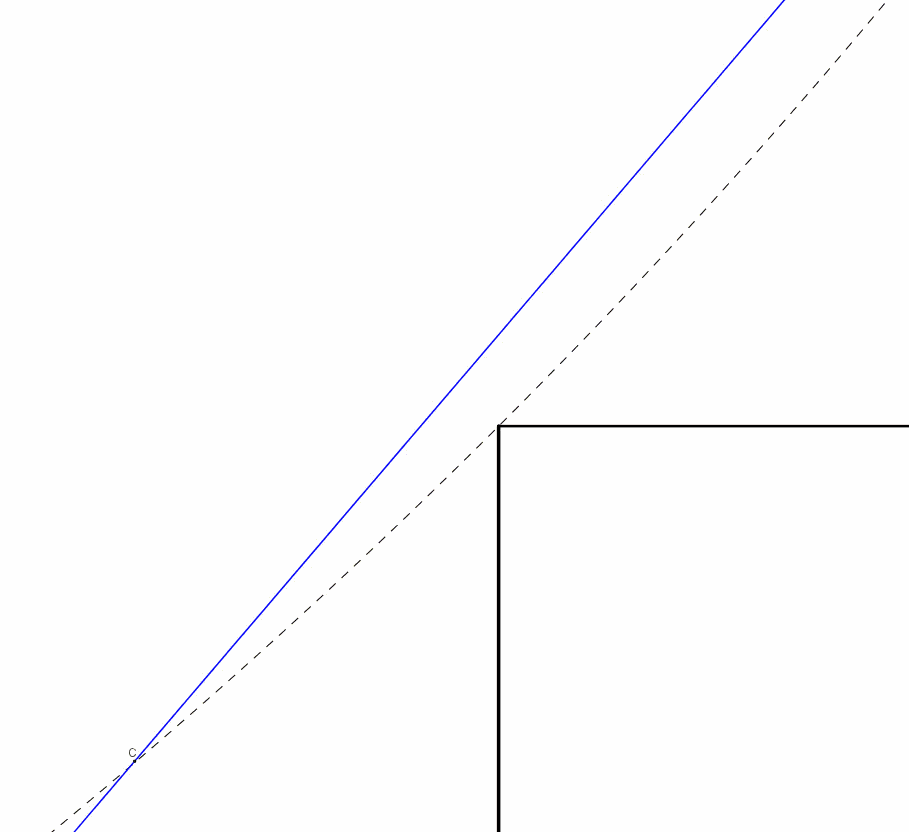Facciamo prima delle osservazioni preliminari, spero che siano intuitive:A parità di angolo  formato con  l'orizzontale le lastre di lunghezza massima vanno cercate in quelle che in un certo istante del movimento toccano le due pareti e lo spigolo del corridoio (quella tratteggiata nel disegno non sta dentro il corridoio).  Vogliamo per prima cosa risolvere il seguente problema: scritta la lunghezza e dell'asta che tocca tutti e tre i punti citati (A,B,S nel disegno qui sotto) in funzione di , trovare  per quale angolo tale lunghezza è minima, e trovare anche tale lunghezza

esprimiamo la lunghezza L in funzione di :

questa è una funzione continua definita in 

Calcoliamone la derivata:

questa si annulla quando  cioè quando 

essendo  compreso fra   ed essendo inoltre i due limiti, per x tendente a zero e per x tendente a  entrambi + infinito, nel punto in cui sia annulla la derivata ha un minimo per  ;

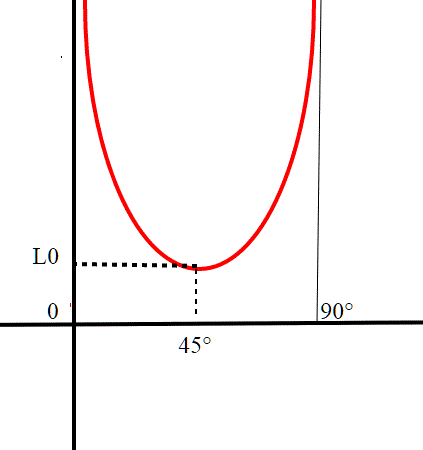
calcoliamo il valore di L per tale angolo e lo chiamiamo L0:

questo è quindi il minimo valore dei segmenti che toccano lo spigolo e le due pareti ortogonali del corridoio; noi stiamo cercando la soluzione del nostro problema nella famiglia di segmenti che toccano i tre punti; chiaramente essendo L0 il minimo esso passa in ogni posizione dell'angolo da , quindi è il più grande dei segmenti contenuti in funzione di .

Come minima distanza fra i segmenti di quel tipo , non ci sono dubbi che L0 sia quella minima. Però noi dobbiamo assicurare che esista un movimento fisico che faccia passare la lastra.

Qualcuno potrebbe obiettare: ma da quella posizione di 45° il segmento (asta) può muoversi? O resta incastrato?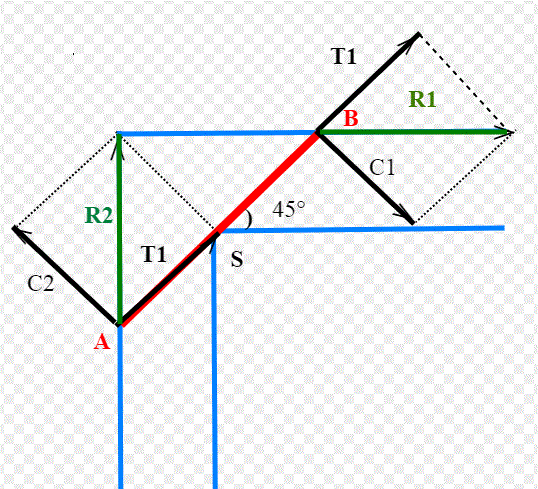

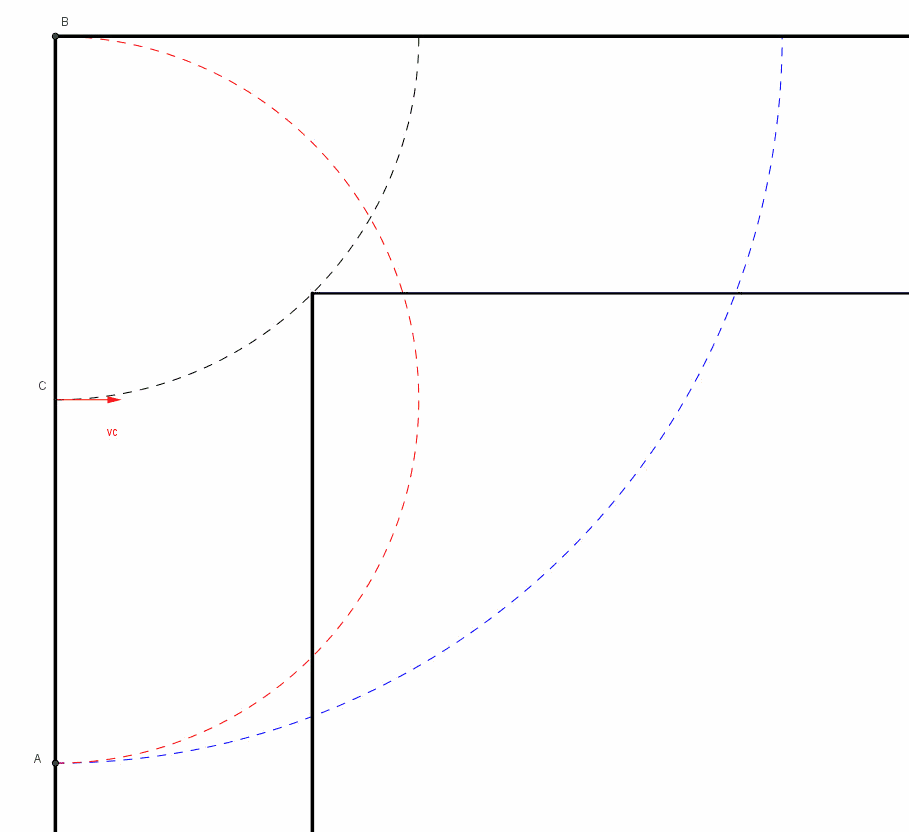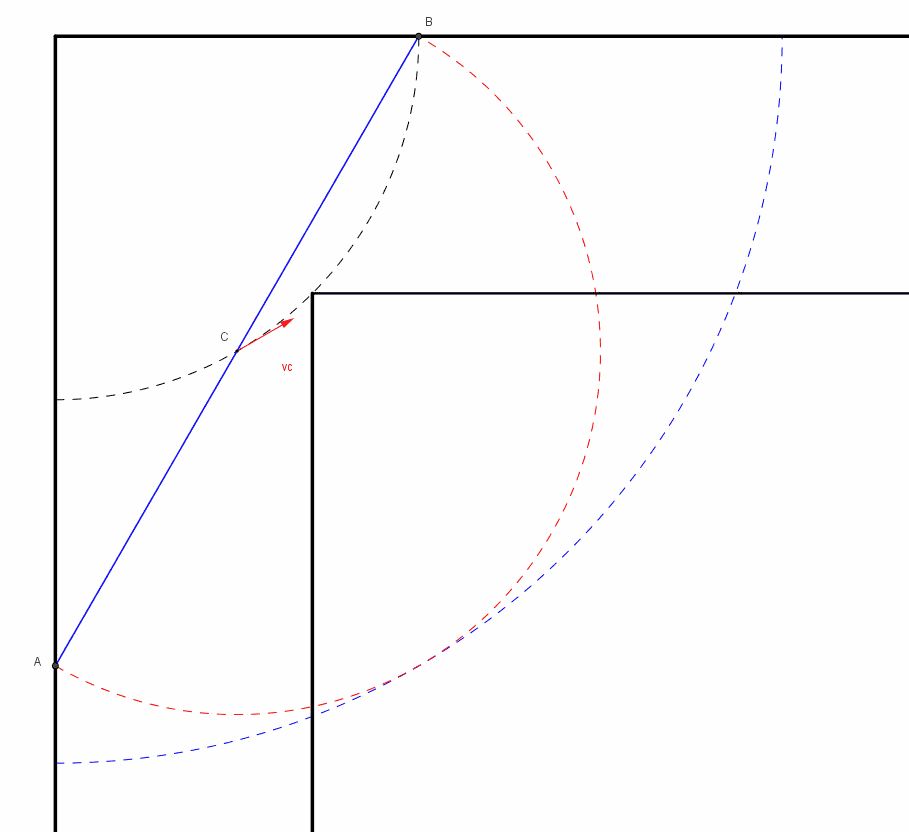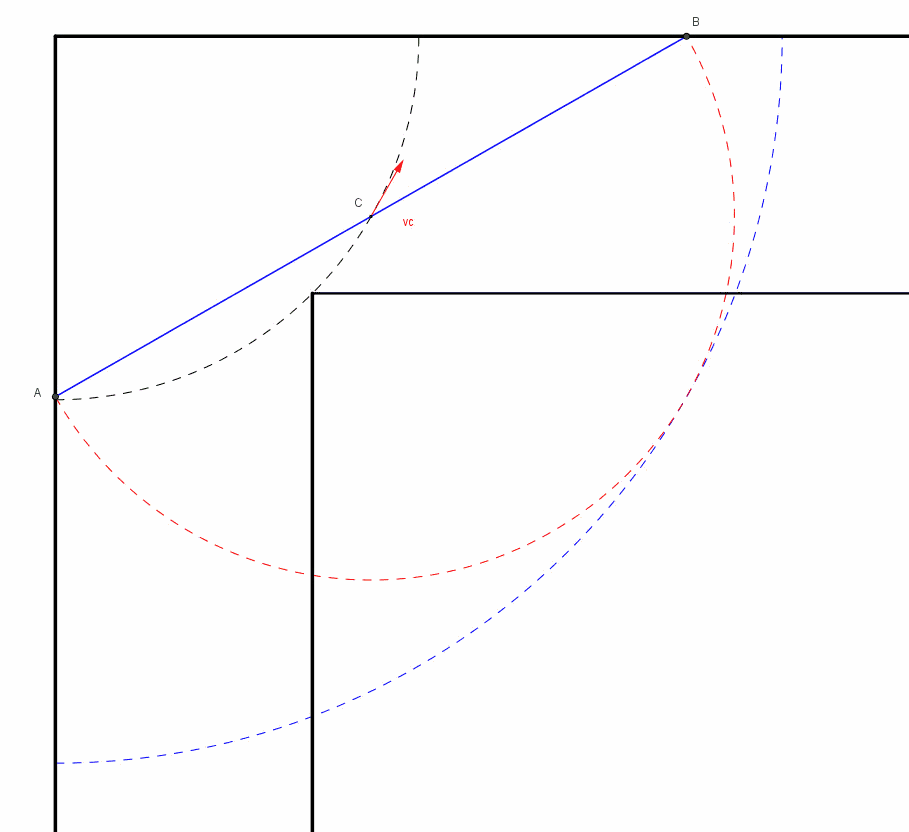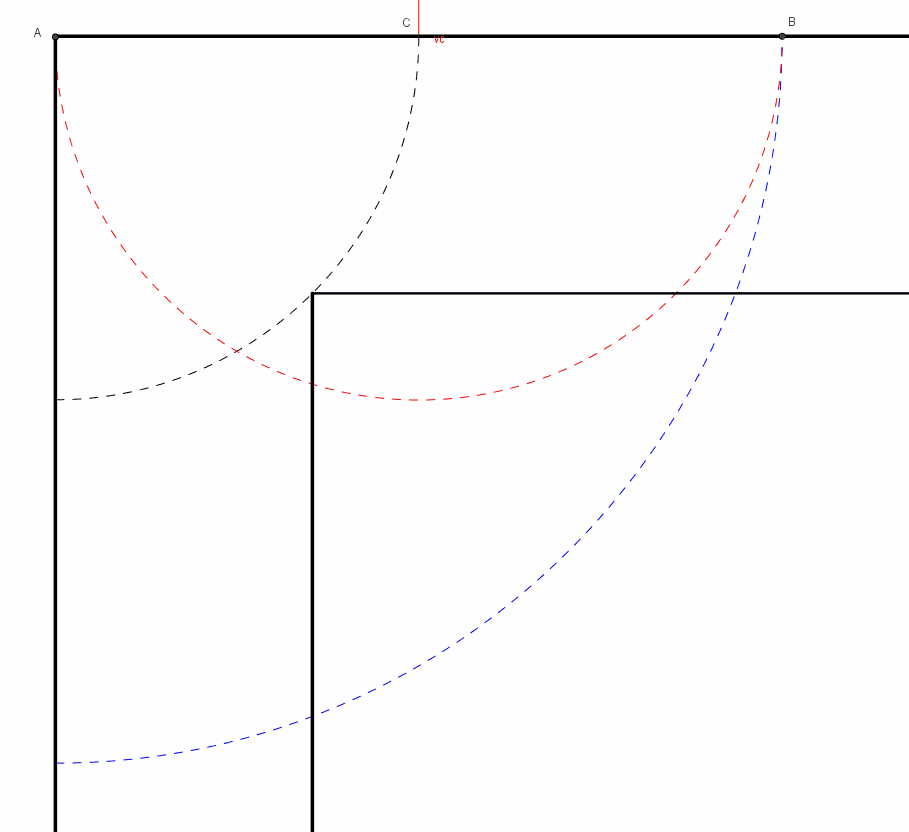
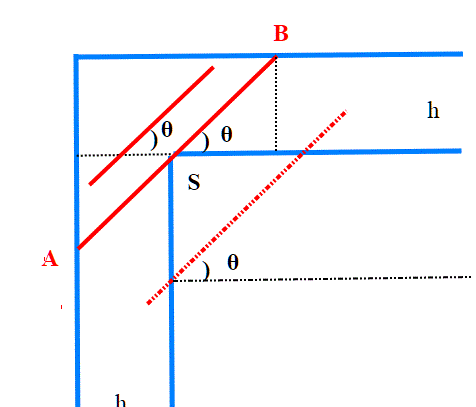
pensiamo ad una rotazione istantanea dell'asta AB attorno allo spigolo S, unitamente ad una traslazione nella direzione dell'asta. Stiamo quindi parlando di una rototraslazione. I vettori C1 e C2 rappresentano la rotazione istantanea di A e B, e sono quindi ortogonali ad AB. La traslazione T1 è diretta invece nella direzione dell'asta, con verso da A a B; possiamo scegliere la velocità angolare istantanea in modo che i moduli delle due velocità  |C1|=|C2|=|T1| siano uguali. Notare che|C1|=|C2 | perchè S è il punto medio.Questo matematicamente si può sempre fare . Le risultanti R1 e R2 che agiscono rispettivamente su B e su A risultano parallele alle rispettive pareti che sono a contatto con gli estremi. Quindi il punto medio di AB ruota attorno ad S; A scivola nella stessa direzione della parete e così pure B. Lo spostamento è possibile, non va contro i vincoli.

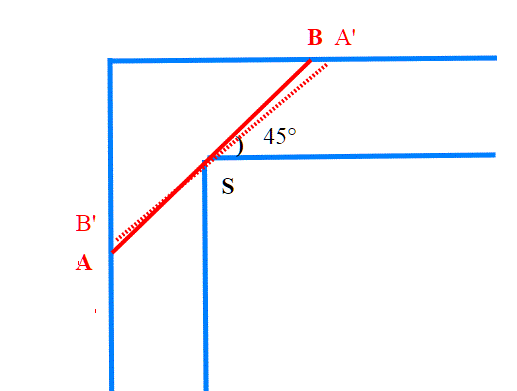
Sappiamo poi che 45° è l'angolo in cui la lunghezza dell'asta è minima; appena si sposta da quella posizione, lo spazio fra i tre punti aumenta, quindi l'asta sta dentro comodamente, e possiamo ruotarla pian piano fino  a raggiungere la posizione orrizzontale.

Quindi AB esce dalla posizione, ma visto la simmetria può anche entrare.Infatti essendo L0 il valore minimo sia che aumentiamo che diminuiamo l'angolo la lunghezza per i tre punti aumenta. Se qualcuno possa avere ancora dei dubbi che AB possa trovarsi in quella posizione, potremmo anche dire che abbiamo costruito il corridoio attorno alla lastra, e poi la abbiamo fatta uscire.

Se invece supponiamo che la lastra tocchi i tre punti e l'angolo sia diverso da 45° possiamo eseguire la rototraslazione solo da una parte, e precisamente quella che fa aumentare l'angolo nel caso esso sia  maggiore di 45°, mentre se l'angolo è minore di 45° quella che fa diminuire l'angolo. Basta appoggiarsi al grafico della funzione  per capirlo. Questo ancora una volta conferama che L0=L(45°) è la massima lastra che può passare.

Nel caso l'angolo sia minore di 45° e ll lastra tocca i tre punti può tornare solo indietro

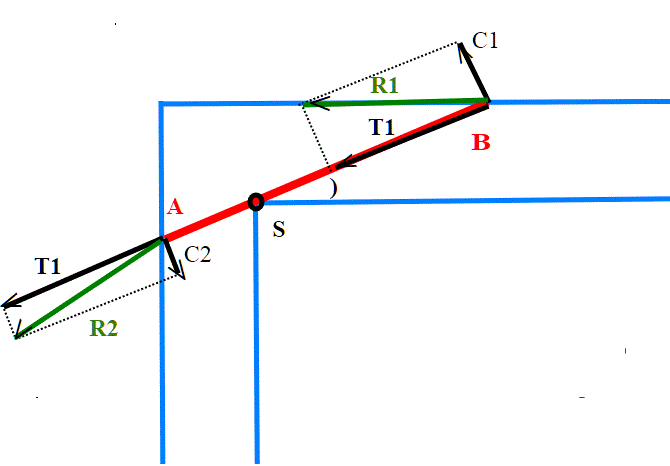
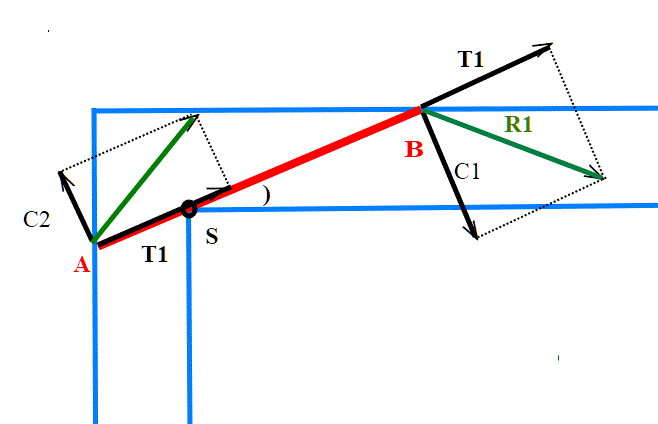
Le due animazioni che proponiamo forniscono una conferma alternativa della possibilità del movimento, rendendo direttamente visibile il vettore spostamento del punto medio.

QUI trovate tutti i quiz del Club dei Maghi