QUIZ: Lo specchio di Quazel */**/***/****
Un quiz a difficoltà variabile per il nostro amico Quazel, che torna finalmente a farci visita dopo l'incontro che abbiamo avuto Natale. Ricorderete certamente la questione delle “infinite luci” per gli addobbi che aveva deciso di acquistare, tanto gli erano piaciute. Un vero affare per quell'elettricista che, oltre a vendere una insperabile quantità di lampadine, aveva avuto il privilegio di imparare, gratis, la raffinata tecnologia dei collegamenti elettrici di Quazelandia.
Ormai le visite di Quazel sono diventate abituali. Si direbbe che provi una forma di nostalgia, tipo “mal d'Africa”, per il nostro pianeta che lo porta a tornare da noi appena gli è possibile.
Questa volta ha addirittura deciso di acquistare una seconda casa, arredarla e passarci le vacanze e qualche “ponte” quazeliano.
Però, appena ha iniziato a programmare il trasloco, si è imbattuto in un potenziale problema.
Tra le varie suppellettili che si devono trasferire dal disco volante con cui sono state trasportate, c'è uno specchio molto particolare. 
Appartiene da tempo immemorabile alla famiglia di Quazel e, oltre a servire a guardarcisi dentro (come è normale per ogni specchio), ha anche un'importante funzione di “video-chiamata” per comunicare con amici e parenti. Insomma, una specie di cellulare gigante.
E', come capite, un oggetto piuttosto delicato che durante il trasloco non deve subire urti o vibrazioni e che è meglio trasportare con il lato maggiore orizzontale, senza sottoporlo a rotazioni; insomma: non si deve “mettere in piedi”.
La misura di questo specchio è decisamente grande e questo lo rende particolarmente utile perché, nonostante l'aspetto giovanile, il nostro Quazel è già nonno di vari nipotini e tra figli, nipoti, cuginetti, e parenti vari, quando lo video-chiamano, inquadrandosi fianco a fianco, finiscono per occupare tutto lo schermo.
Ma qual è il problema, allora? Basta trasportare con cura questo specchio-celllulare alieno, tenendolo in orizzontale fin dentro la stanza in cui andrà collocato, e tutto è OK.
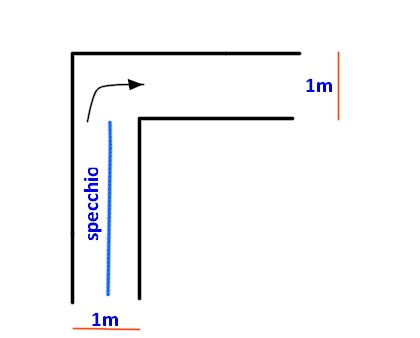
Ebbene, la cosa non è così semplice... perché, per arrivare alla sala dove Quazel intende appenderlo, occorre passare per un corridoio a forma di L, i cui bracci sono larghi esattamente un metro.
Questa figura ci aiuterà a capire meglio...
La lunghezza dello specchio consentirà il passaggio senza che vi siano interferenze con le pareti del corridoio e il minaccioso spigolo interno?
Dopo aver preso più volte le misure, il nostro amico alieno è certo che la larghezza del corridoio è esattamente di un metro e in nessun punto sono presenti restringimenti, neppure piccolissimi.
Ma quale sarà, secondo voi, la misura della lunghezza di questo benedetto specchio perché possa effettivamente passare lungo il corridoio a L? In altre parole, qual è la massima lunghezza della lastra che consentirà di completare il percorso da compiere?
Attenzione: Non preoccupatevi di problemi come lo spessore della lastra: è un cristallo di una sottigliezza tale da poterla trascurare. Non state neppure a chiedervi come faranno a maneggiarlo gli operai senza rischiare di schiacciarsi le dita. Certo, il fatto che i traslocatori abbiano 5 dita invece delle normali 4 dei quazeliani, complica un po' le cose, ma Quazel ha progettato delle ventose antigravità che consentiranno una presa sicura e senza interferenze con le pareti del corridoio.
Avanti con le vostre soluzioni... come potete vedere dal numero variabile di asterischi, il livello di difficoltà può anche essere basso dando una soluzione intuitiva. I più esperti, invece potranno alzare il livello a loro piacimento, purché non rompano lo specchio! Quazel non è certo superstizioso, ma preferisce non rischiare 
QUI la soluzione
QUI tutti i quiz del Club dei Maghi
9 commenti
Così ad occhio direi che il limite di lunghezza è di 2,82 metri... ma potrei sbagliarmi.
Paolo
“Ma qual è il problema, allora? Basta trasportarlo con cura tenendolo in orizzontale fin dentro la stanza in cui andrà collocato, e tutto è OK.”
La lunghezza l e l'altezza h in orizzontale?
Sfiorando il minaccioso spigolo interno, la lunghezza supera il valore di 1 m se h varia da 0 - 0,99.
Se h = 1 m la lunghezza massima vale 1 m, area di 1 m²
Se invece h = 0 l = 2/sen 45° = 2,828 m
Ci congratuliamo con i solutori che, nei loro commenti, hanno suggerito con precisione il valore del limite superiore della lunghezza dello specchio.
Ora che questa dimensione è stata individuata, viene da chiedersi quale traiettoria verrà percorsa durante il movimento dal punto centrale della lastra.
Immaginiamo che nella posizione iniziale lo specchio sia accostato alla parete di sinistra e il suo estremo più avanzato tocchi la parete di fondo.
Ribadiamo che la posizione dello specchio, durante il trasporto, va intesa"di costa".
Analizzando lo spostamento potremmo avere il dubbio che, ad un certo punto, lo specchio resti "incastrato".
Quali ragionamenti si possono fare a questo proposito?
Io ho provato a fare questa figura... cercando di indicare anche il presunto movimento del centro.
Si tratta di calibrare il movimento di rotazione, quello verso l'alto e quello verso destra...
Paolo
ops, dimenticavo il movimento del centro l'ho ricavato così...
Paolo
Un piccolo sforzo e arriviamo ai quattro asterischi! Ci siamo quasi!
Ho provato a calibrare i tre movimenti...
La figura mostra che affinché la barra possa passare è necessario oltre a ruotarla anche spostarla verso destra (asse x) e verso l'alto (asse y).
Di quanto bisogna spostarla?
Dalla figura emerge che ogni volta che l'angolo cambia (rotazione) il centro della barra si deve spostare in x di d/2 (cos α) e in y di d/2 (1-sin α), dove d/2 è la metà della lunghezza della barra.
Ne segue che ciò che cambia nel tempo è solo l'angolo, pertanto alla rotazione di un certo angolo, segue uno specifico spostamento verso destra e verso l'alto.
In concreto al variare dell'angolo α deve seguire uno spostamento verso destra pari a:
Δ x = d/2 (cos α)
e verso l'alto di:
Δ y = d/2 (1-sin α)
All'inizio, quando la barra è verticale, l'angolo “α” è di 90°; quindi:
Δ x = d/2 (cos 90°) = d/2 (0) =0
Δ y = Δ y = d/2 (1-sin 90°) = d/2 (1-1) = 0
Quando il centro della barra ha raggiunto l'angolo β di 45° (barra rossa):
Δ x = d/2 (cos 45°) = d/2 0,7071
ma d/2 = ½ √8 = √2
Δ x = √2 (0,7071 ) = 1 metro
Δ y = Δ y = d/2 (1-sin 45°) = d/2 (1-0,7071) = d/2 0,2929 = 0,4142 metri
Se faccio variare tutte e tre gli spostamenti nel tempo, ottengo delle relazioni tra velocità:
Δ φ/Δ t = ω
Bisogna però considerare che all'inizio l'angolo è di α 90°, per cui la variazione Δ φ indica di quanto questo è diminuito, pertanto l'angolo variabile che serve per confrontare seno e coseno è pari a:
αvar = (90°- Δ φvar )
Δ x/Δ t =Vx =d/2 (cos αvar)/ Δ t
Δ y/Δ t = Vy = d/2 (1-sin αvar)/ Δ t
Spero di non aver detto qualche sciocchezza...
Paolo
il punto cruciale resta sempre però il superamento della posizione a 45 in cui tutti e tre i punti toccano (centro e i due estremi); é l unico angolo che genera una perfetta simmetria di movimentazione; passa o non passa in questa posizione? Bisognerebbe ragionare con dei vettori..
A mio avviso passa anche se proprio per un pelo...
comunque per rispetto di Quatzel, consiglierei di usare qualche millimetro di tolleranza.. (fermiamo la virgola a 2,8 metri di lunghezza dello specchio).
Dunque, vediamo se riesco a spiegare perché dovrebbe passare.
Prima avevo posto alcune condizioni affinché lo specchio possa passare, per cui ad una certa rotazione deve corrispondere anche un certo spostamento verso destra e verso l'alto.
Δ x =d/2 (cos α) …. e …. Δ y = d/2 (1-sin α)
ma α = (90°- φ) e poiché l'angolo φ cambia nel tempo (rotazione della barra), cambia nel tempo anche l'angolo α, dato che (90°- φ) rappresenta l'intervallo angolare di cui è ruotata la barra in un certo intervallo di tempo Δt.
Quindi, considerando d/2= √2, la prima equazione diventa:
Δ x =√2 (cos (90°-φ))
ma cos (90°-φ) = sin (φ)
Δ x =√2 sin (φ)
Δ y = d/2 (1-sin α)
Δ y = √2 (1-sin (90°- φ))
ma sin (90°- φ) = cos φ
Δ y = √2 (1- cos (φ))
Se si pone una velocità di rotazione ω costante, giusto per sincronizzare i movimenti, è possibile ricavare il valore dell'angolo φ in un certo istante:
ω = Δ φ/Δ t
φ = ω Δ t
Pertanto, le due equazione si possono scrivere come:
Δ x =√2 sin (ωΔt)
Δ y = √2 (1- cos (ωΔt))
Ovviamente ω Δt indica il valore dell'angolo φ dopo un certo intervallo di tempo Δ t.
Se si voglio confrontare le velocità basta dividere tutto per Δ t:
Δ x/Δ t = √2 sin (ωΔt)/Δ t
Vx = sin(ωΔt) √2 /Δ t
Δ y/Δ t = √2 (1- cos ω Δt)/ Δt
Vy = (1- cos (ωΔt))√2 / Δt
ma anche:
Vy/Vx = (1- cos (ωΔt))√2/Δ t sin (ωΔt)√2/ Δ t
Vy/Vx = (1- cos (ωΔt))/sin (ωΔt)
Vy = Vx (1- cos (ωΔt))/sin (ωΔt)
Vx = Vy sin (ωΔt) /(1- cos (ωΔt))
Per quanto riguarda la velocità angolare, si può ricavare quella tangenziale, dato che:
ω = Vt/r
dove Vt è la velocità tangenziale e r è uguale a d/2 ed ω è espressa in radianti
ω = Vt/√2
Vt = ω √2
Per esempio ponendo ω =1°/sec (ma si potrebbe scegliere un'altra velocità, bisogna vedere quanto in fretta si vuole fare il lavoro di spostamento), dopo 45 secondi:
ω =1°/sec …. e Δ t = 45 sec
Vt = ω √2
1° = 0,0174 radianti
Vt = 0,0174 √2 = 0,0246 mt/sec
φ = ω Δ t = 1°/sec 45 sec = 45°
Vx = sin (ω Δ t) √2 /Δ t = sin(45°) √2 /45 = 1/45 = 0,0222 mt/sec
Δ x = VxΔ t = (0,022) 45 = 1 metro
Vy = (1- cos (ω Δ t))√2 / Δ t
Vy = (1- cos (45°))√2 /45 = 0,4142/45 = 0,0092 mt/sec
Δ y = VyΔ t = (0,0092) 45 = 0,4142 metri
Variando l'intervallo di tempo:
Δ t = 48 sec
φ = ω Δ t = 1°/sec 48 sec = 48°
ovviamente Vt come modulo non cambia, dato che Vt = ω √2 e la velocità angolare è sempre la stessa.
Vx = sin (ω Δ t) √2 /Δ t = sin(48°) √2 /48 = 1,05/48 = 0,0218 mt/sec
Δ x = VxΔ t = (0,0218) 48 = 1,05 metri
Vy= (1- cos (48°))√2 /48 = (0,468) /48 = 0,0097 mt/sec
Δ y = VyΔ t = (0,0097) 48 = 0,468 metri
Se l'intervallo è di soli 30 secondi:
φ = ω Δ t = 1°/sec 30 sec = 30°
Vx = sin (ω Δ t) √2 /Δ t = sin(30°) √2 /30 = 0,7071/30 = 0,2357 mt/sec
Δ x = VxΔ t = (0,2357) 30 = 0,7071 metri
Vy = (1- cos (30°))√2 /30 = (0,189)/30 = 0,006 mt/sec
Δ y = VyΔ t = (0,006) 30 = 0,189 metri
Pur mantenendo costante la velocità angolare, le due velocità Vx e Vy cambiano continuamente, al fine di evitare che la barra possa incastrarsi... e sembra che ce la facciano!
Tutti questi calcoli li ho usati per trasformare questi tre movimenti in tre vettori (Vt; Vx e Vy) che ho applicato ai due estremo della barra... e sembra che questa possa passare senza incastrarsi, però non si sa mai...
Paolo