Categorie: Relatività
Tags: invisibile lati Pappo Pippo quiz relatività ristretta torta quadrata visibile visioni relativistiche
Scritto da: Vincenzo Zappalà
Commenti:10
QUIZ: come vedere (non insieme) tre colori di una torta quadrata**
Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.
Continuiamo il nostro viaggio in balia degli scherzi della luce, attraverso un nuovo quiz che vede interpreti, tanto per cambiare, Pippo e Pappo. La difficoltà è relativa e ormai l’argomento dovrebbe essere ben chiaro a tutti coloro che hanno seguito i quiz precedenti. Questa volta vogliamo anche una semplicissima quantificazione del risultato. Data la semplicità, chiederei ai più esperti di aspettare un paio di giorni prima di dare la risposta (intanto preparate le animazioni…).
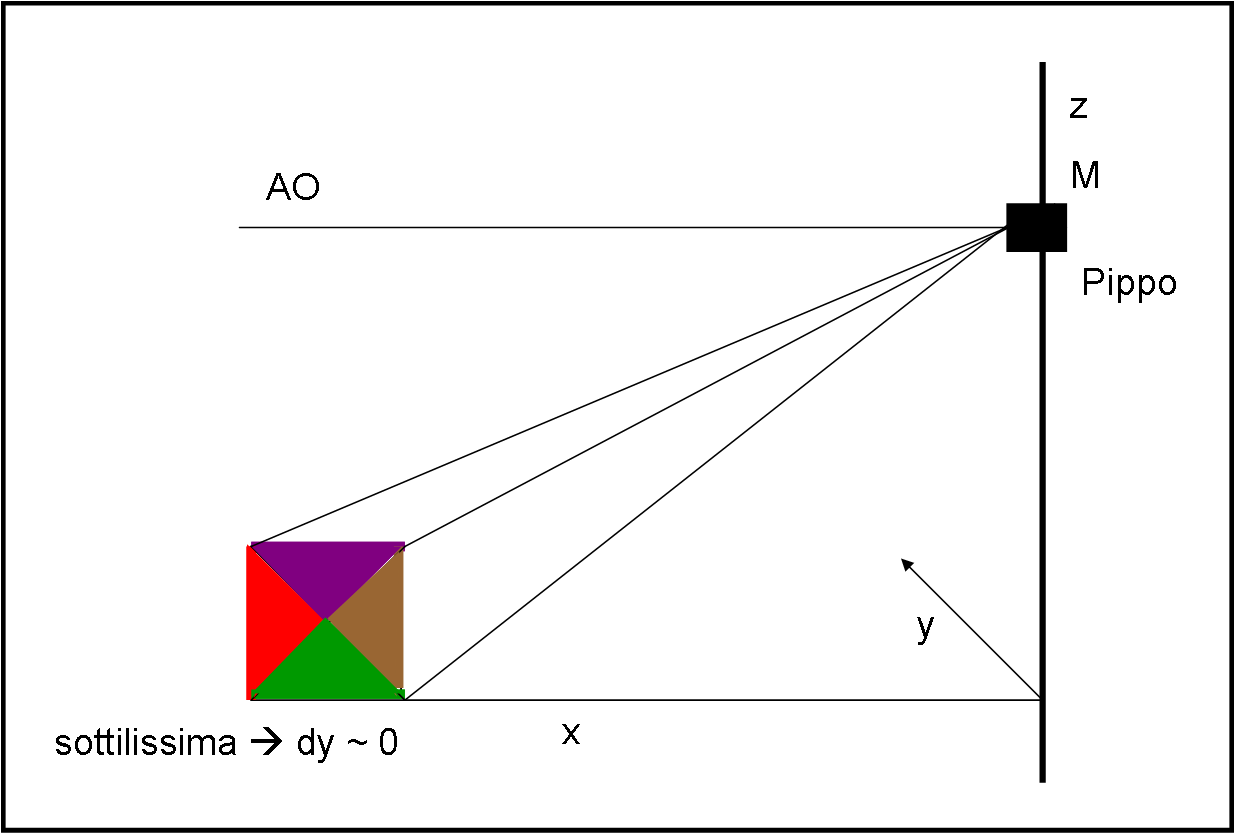
La mamma di Pippo e Pappo ha preparato un altro manicaretto: una torta quadrata sottilissima con quattro tipi di crema. Possiamo considerare praticamente trascurabile il suo spessore, che comunque mostra chiaramente il colore dei vari lati. La posizione di partenza è quella raffigurata nella figura che segue. Pippo ha una macchina fotografica M di cui AO è l’asse ottico.
Pappo dice a Pippo di prendere una fotografia della torta ferma. Ovviamente, Pippo può fotografare solo due colori (il marrone della cioccolata e il viola dei mirtilli). Poi Pappo chiede a Pippo: “Cosa devo fare affinché tu riesca a fotografare la crema di fragola (rossa)? Ovviamente, però, non posso ruotare la torta e nemmeno farle superare l’asse z. In poche parole posso solo muoverla lungo l’asse x fino a un certo punto”. Poi aggiunge: “Vorrei che tu mi dicessi cosa deve succedere esattamente, perché capiti ciò che ho detto di riuscire a fare, attraverso una formula matematica semplicissima… Tieni conto, nel caso ce ne fosse bisogno, anche della Relatività Ristretta”.
Come al solito, solo se Pippo saprà dire esattamente cosa deve fare Pappo con la torta, riuscirà a mangiarne la metà.
Qualsiasi grafico esplicativo è decisamente gradito.
P.S.: cercando nell'archivio del Circolo... la risposta c'è già...
QUI la soluzione
QUI tutti gli articoli/quiz dedicati alle visioni relativistiche






10 commenti
AVVISO PER TUTTI: non è necessario che si vedano i tre colori contemporaneamente. Nella prima foto ci sono senz'altro il viola e il marrone. Basta che nella seconda compaia tutto il lato rosso.
Assodato che nessuno vuole tentare di risolvere qualcosa che è già stato praticamente spiegato nelle puntate precedenti... lascio VIA LIBERA ai maghi, maghetti e affini. Forza, non deludetemi!
Cosa penseranno Lampa, Terrel e Penrose di questo silenzio?
Paolo
Eh sì, caro Paolo... cosa penseranno mai?
a dopodomani!!!!
Chiamo A, B, C, E i 4 vertici del quadrato cominciando da quello in basso a sinistra e procedendo in senso antiorario. Sia A0 la posizione di A all'istante iniziale. Perché nella foto si veda tutto il lato rosso della torta quadrata, Pappo dovrà muovere la torta verso Pippo a velocità relativistica v tale che il fotone FA partito da A0 all'istante iniziale, muovendosi verso M, non vada a impattare sul lato AE della torta nel frattempo spostatasi verso destra. Si tratta, quindi, di stabilire una relazione tra v e c che soddisfi alla suddetta condizione geometrica. Al limite, all'istante t la retta A0M passa per E(t). Se allora considero il triangolo rettangolo A0AE e inoltre indico con l il lato del quadrato, dovrà essere:
cioè
da cui
Se inoltre considero i triangoli rettangoli A0AE e AoDM (D è il punto di coordinate d,0) , essi sono simili per cui:
da cui
sostituisco la (2) nella (1) ottenendo alla fine:
Questo è il valore minimo che dovrà avere v affinché il fotone FA riesca a "scansare" il lato AE che si sta spostando verso destra, e quindi riesca ad arrivare ad M, facendo così vedere il lato rosso nella foto. Dalla suddetta formula si vede che il rapporto tra v e c dipende dal rapporto tra H e d, in definitiva dalla posizione della macchina fotografica rispetto alla posizione iniziale della torta quadrata.
Allego una prima animazione realizzata per v=0,95 c ( con d=40 e H=20). Non ho tenuto conto della contrazione delle lunghezze.
E' curioso osservare che , in questo modo, mentre diventa visibile tutto il lato rosso del quadrato, scompare invece alla vista almeno la parte bassa del lato marrone (ho provato solo con il punto B)! Il fotone FB partito da B all'istante tB tale da andare di pari passo con i fotoni partiti prima da A0 ed E, infatti, appena partito resta subito occultato dal quadrato nella direzione di M, per cui in pratica il punto B del quadrato diventa invisibile da M.
caro Arturo,
(1) sarebbe bello far vedere cosa si vede della torta, ossia la forma che assume considerando i punti di partenza che giungono nello stesso istante in M, tenendo anche conto della contrazione delle lunghezze. Quella tracciata alla fine è solo la visione, ma sarebbe bello vedere tutta la deformazione del quadrato...
(2) più rapidamente dell'utilizzo delle altezze di M e del quadrato o cose simili, basta imporre una relazione tra v e c, utilizzando l'angolo sotto cui si vede la macchina. La relazione diventa di banale comprensione da parte di tutti...
Faccio presente, come Paolo ha già capito, che la situazione è una generalizzazione della rotazione di Lampa & co. trattata qualche tempo fa, per un osservatore all'infinito...
(2) ok, smanettando con la radice al denominatore e sapendo che H = d tan , dove
, dove  è l'angolo formato dalla congiungente A0 con M e l'asse x , alla fine si ha
è l'angolo formato dalla congiungente A0 con M e l'asse x , alla fine si ha
v = c cos
a cui si poteva arrivare immediatamente considerando il triangolo rettangolo prima invocato, cioè AoAE.
In pratica, le due relazioni sono due espressioni della stessa realtà.
perfetto Arturo! In poche parole semplici: "Se la componente della velocità della luce lungo l'asse x è minore della velocità v si vede il lato rosso, altrimenti si vede quello marrone..." Ovviamente, tutto dipende dalla posizione della macchina M...
In queste animazioni ho congelato la posizione di ciascun punto del quadrato nel momento che emette il fotone che arrivera alla macchina nel momento dello scatto. Si crea una figura fittizia che mi sembra possa mettere in evidenza graficamente la visibilità o meno dei lati rosso e marrone. Peraltro la figura è fittizzia nel lato ripreso nell'animazione, ma dal punto di vista della macchina corrisponde all'immagine impressa.
Nelle prime due figure v=0,9 c
e questo è lo scatto della macchina con il lato rosso visibile.
Queste altre sono per v=0,3 c
con il lato rosso non visibile ed il lato marrone visibile.
Vi sottopongo un dubbio.I fotoni che dal lato rosso vanno verso la macchina, al momento della emissione, dovrebbero andare verso l'interno del materiale. Possono esistere anche nel caso di diffusione di una sorgente di luce esterna?
caro Fabry,
per angoli sufficientemente alti, i fotoni non vanno all'interno del materiale dato che lui viaggia più in fretta della componente x della luce.