Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.

 

I lettori più “fedeli” e con ottima memoria (vero Paolo?)  avranno riconosciuto in questo quiz la rotazione di Lampa-Penrose-Terrell, che avevamo già trattato, in modo semplificato, in un quiz e in una risposta molto articolata.

In quel caso (QUI) avevamo posto la macchina fotografica a una distanza infinita da un cubo, in modo da avere le traiettorie dei fotoni esattamente perpendicolari alla direzione del moto. Ci eravamo accorti che la contrazione di Lorentz non si riesce a fotografare, a causa della “lentezza” della luce e all’apparizione quasi magica della faccia del cubo che dovrebbe essere invisibile. Avevamo anche notato che questa deformazione corrisponde esattamente a una apparente rotazione del cubo, da cui il nome dell’effetto.

Nel caso di Pippo e Pappo, la faccenda è leggermente più complicata, in quanto abbiamo a che fare con una macchina fotografica posta molto vicina alla torta (quadrata) che si muove a velocità relativistica. Ne segue che l’angolo tra direzione del moto e direzione della macchina fotografica è un parametro fondamentale e guida, in qualche modo, il risultato finale.

La condizione essenziale affinché si riesca a fotografare il lato rosso o il lato marrone dipende dalla componente della velocità della luce lungo la direzione del moto.

In poche parole, se la componente orizzontale (lungo la direzione del moto) della velocità della luce (diretta dal quadrato alla macchina fotografica) è più corta della velocità di spostamento della torta si riesce a vedere il lato rosso (intuitivamente nascosto nella realtà quotidiana). Se invece la componente della luce è maggiore della velocità del quadrato, tutto rientra nella normalità (si fa per dire…) e si vede il lato marrone (già visto da Pippo).

Più semplicemente ancora, data una certa velocità di spostamento, bisogna scegliere la posizione della macchina M o, analogamente, data la posizione della macchina, bisogna scegliere una velocità sufficiente per lo scopo.

Vediamo quanto detto finora, attraverso il semplice schema di Fig. 1.

Nella parte alta si nota cosa capita a un fotone che parta dal lato rosso del quadrato, nell’istante (1). Il quadrato si muove lungo l’asse x più velocemente di quanto non faccia la componente della velocità della luce lungo questa direzione. Il fotone si ritrova, perciò, nell’istante (2) più indietro del lato rosso del quadrato, trascinato verso l’alto dalla componente verticale di c. Il vantaggio del quadrato (d) continua e diventa ancora più grande all’istante (3). Infine, all’istante (4) la via è completamente libera per il fotone che sta per superare, benché in ritardo, la parte superiore del lato rosso del quadrato: non gli resta che dirigersi verso la macchina fotografica M.

Ben diversa è la situazione per il fotone che parte dal lato marrone del quadrato. Lui vorrebbe lanciarsi verso la macchina fotografica, ma il quadrato è più rapido, lungo la direzione x, e, quindi, il fotone non riesce nemmeno a muoversi in quanto viene immediatamente assorbito dal lato del quadrato. Nessun fotone riesce a lasciare il quadrato e il lato marrone non può che risultare invisibile per la macchina fotografica M.

Si ha un risultato decisamente lontano da ciò che capita nelle condizioni “normali” di tutti giorni. Il quadrato vedrà impresso, sul piano focale, il lato che dovrebbe essere sempre nascosto alla vista. Ricordiamo, infatti, che il quadrato NON può superare la verticale rispetto alla macchina M.

In semplici parole matematiche, possiamo dire che per poter vedere il lato rosso -e non quello marrone- è necessario che valga la relazione:

v > c cosα

dove α è l’angolo formato tra la direzione del moto del quadrato e la direzione della macchina fotografica M.

Per avere la massima sicurezza che questo accada, le condizioni migliori sono quelle in cui l’angolo venga misurato dal limite superiore del lato rosso. Se per lui vale la relazione precedente, essa deve valere sicuramente per tutti quelli inferiori (aumenta l’angolo α e quindi diminuisce ancora di più il coseno e, quindi, la componete orizzontale della velocità della luce).

Non vi è sicuramente bisogno di ripetere la Fig. 1 per il caso in cui la componente di c risulti più grande di v (angolo α più piccolo). In questo caso è ovvio che siano i fotoni del lato rosso che non riescono a lasciarlo, venendo subito assorbiti, mentre quelli marroni scappano immediatamente verso la macchina M. La fotografia assume un aspetto più normale…

Vediamo, allora, come si deforma il nostro quadrato nei due casi, regolati dalla direzione di M.

Cominciano (Fig. 2) con quello che permetterebbe a Pippo di guadagnarsi la torta.

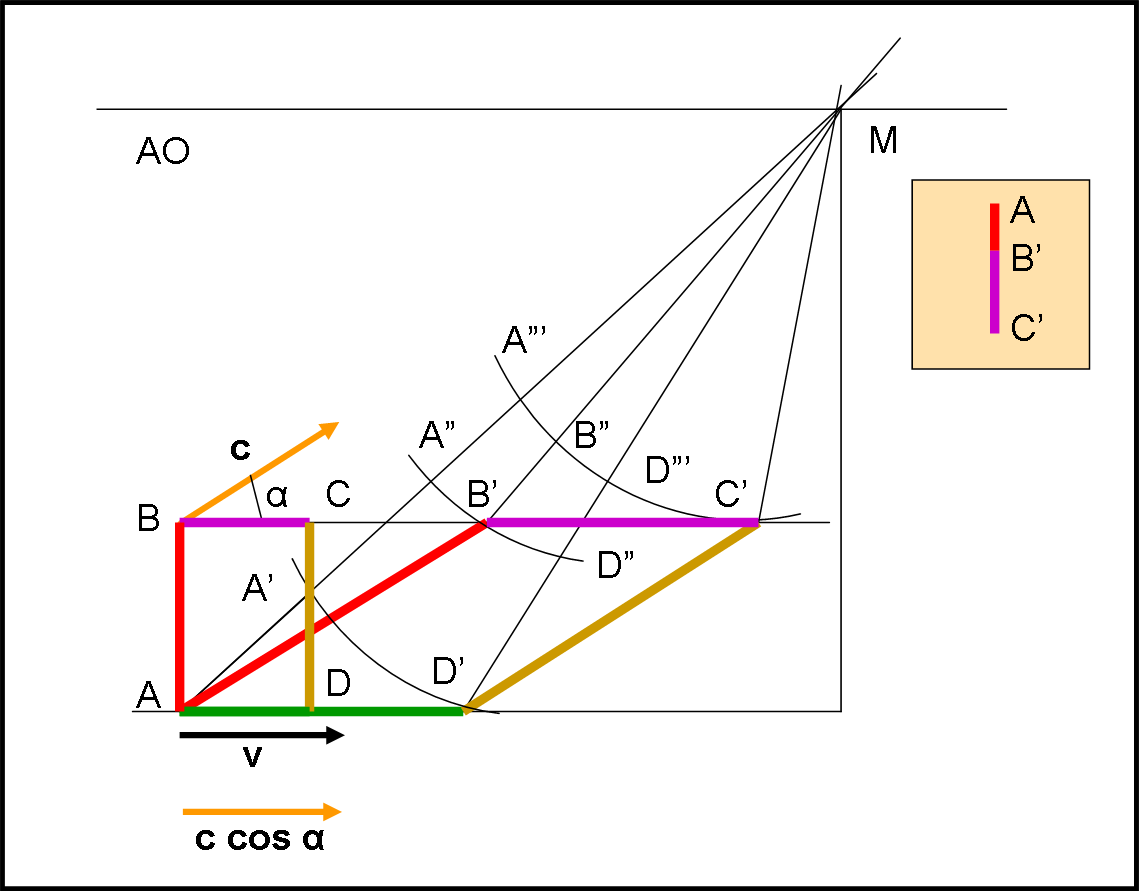
La componente della velocità della luce è minore della velocità con cui si muove il quadrato. Per capire cosa fotograferebbe  M, bisogna far partire i fotoni al momento giusto, considerando anche quelli che non possono arrivare. Ragione per cui immaginiamo, per un momento, il quadrato fatto di vetro, trasparente alla radiazione luminosa. Il quadrato è stato contratto a causa della trasformazione di Lorentz.

Per arrivare al giusto tempo su M, deve partire per primo (in realtà i fotoni partono continuamente, ma noi dobbiamo considerarne uno in particolare) quello più lontano dalla macchina fotografica, ossia quello che corrisponde al vertice A. Lui non ha problemi di vetro trasparente oppure no, come abbiamo visto precedentemente e si lancia senza problemi verso M. Il secondo a partire è quello di D, che teoricamente sarebbe subito assorbito. Ma noi lo facciamo comunque proseguire, eliminandolo a tempo debito. Il momento della sua partenza dipende dal percorso già compiuto dal fotone di A. Lui dà il via a D’, quando si viene a trovare in A’, ossia quando le distanze A’M e D’M sono uguali (solo così arriveranno insieme su M). Non ci stupiamo di certo se il lato contratto AD diventa molto più lungo (A’D’), ricordando quanto descritto QUI.

Configurazione analoga si ha per il fotone B. Anche lui deve aspettare quello partito da A e quello partito da D. Il momento fatidico per lasciare il quadrato è quando B’ dista da M lo stessa distanza di A” e D”. B’ è spostato in avanti rispetto a B, ricordando come un righello (AB) perpendicolare alla direzione del moto si piega in avanti (QUI). In realtà, il segmento dovrebbe essere curvilineo, ma la sua lunghezza è talmente piccola, rispetto al caso del righello perpendicolare, che possiamo considerarlo rettilineo.

Non ci resta adesso che identificare il momento della partenza di C. Basta, calcolare la distanza allungata rispetto a B’ con il solito metodo già richiamato e si localizza C’. A questo punto i quattro fotoni proseguono indisturbati fino a M, dato che devono percorrere una distanza del tutto identica. La foto è fatta e ciò che si vede è rappresentato nell'inserto vicino a M (ricordiamo che invertiamo l'immagine)

Non ci rimane, adesso, che riempire la torta e quindi annullare il fotone che viene assorbito dalla sua “pasta”. Lui è, ovviamente, quello proveniente da D’ e, quindi, i lati invisibili risultano essere AD e DC. Pippo vede il lato rosso, dopo aver visto, prima della partenza, anche quello marrone, oltre a quello viola: tre colori, proprio come gli si chiedeva di fare!

Non voglio nemmeno descrivere cosa succede nel caso che Pippo non capisca cosa deve chiedere di fare a Pappo. Basta abbassare di molto la macchina fotografica M e rendere, perciò, molto più piccolo l’angolo α. Adesso è la luce che viaggia più veloce lungo l’asse x e quindi, come mostra la Fig. 3, non si vede più il lato rosso, ma nuovamente quello marrone.

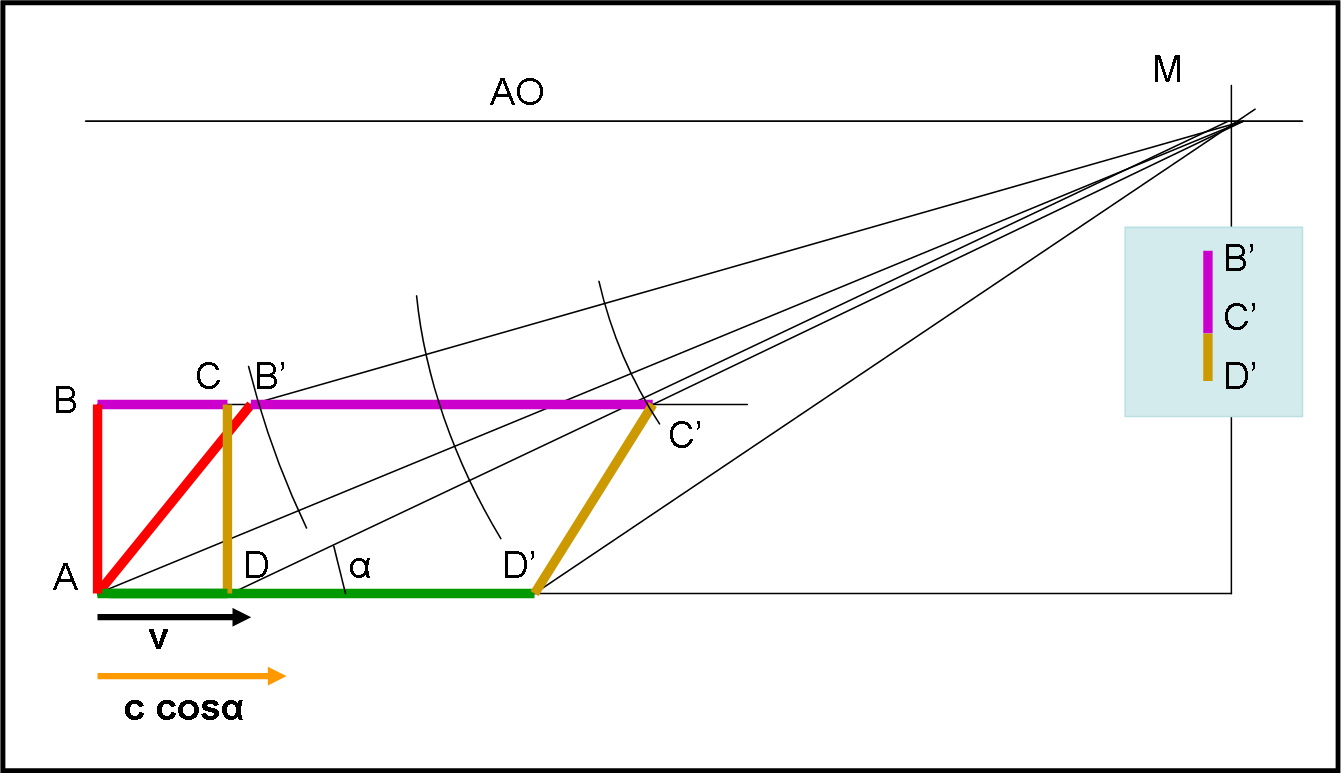
Per questa volta, diamo la vittoria a Pippo (quel Pappo sta diventando troppo saputello…).

La prossima volta concluderemo in bellezza questa serie di articoli, con un viaggio tra i palazzi impazziti di una città. Troveremo, però, uno strano monumento che sembra del tutto alieno nella sua normalità.

A presto!

P.S.: dedicato ai giocatori d’azzardo. Manovrando sapientemente i dadi si possono vincere molti quattrini, senza barare, dato che la velocità relativistica è un tipo di lancio permesso e fa vedere ciò che solitamente non si vede… (è tenuta in conto, ovviamente, anche la prospettiva).

ANIMAZIONE (sotto i dadi fermi, sopra un dado in moto relativistico)

 

QUI tutti gli articoli/quiz dedicati alle visioni relativistiche